Open Journal of Statistics
Vol. 2 No. 5 (2012) , Article ID: 25549 , 7 pages DOI:10.4236/ojs.2012.25067
Effective Truncation of a Student’s t-Distribution by Truncation of the Chi Distribution in a Chi-Normal Mixture
Department of Engineering Physics, McMaster University, Hamilton, Canada
Email: cassidy@mcmaster.ca
Received September 25, 2012; revised October 27, 2012; accepted November 10, 2012
Keywords: Asset Pricing; Student’s t-Distribution; Cauchy; Truncation; Moments; Kurtosis
ABSTRACT
A Student’s t-distribution is obtained from a weighted average over the standard deviation of a normal distribution, σ, when  is distributed as chi. Left truncation at q of the chi distribution in the mixing integral leads to an effectively truncated Student’s t-distribution with tails that decay as exp
is distributed as chi. Left truncation at q of the chi distribution in the mixing integral leads to an effectively truncated Student’s t-distribution with tails that decay as exp . The effect of truncation of the chi distribution in a chi-normal mixture is investigated and expressions for the pdf, the variance, and the kurtosis of the t-like distribution that arises from the mixture of a left-truncated chi and a normal distribution are given for selected degrees of freedom
. The effect of truncation of the chi distribution in a chi-normal mixture is investigated and expressions for the pdf, the variance, and the kurtosis of the t-like distribution that arises from the mixture of a left-truncated chi and a normal distribution are given for selected degrees of freedom . This work has value in pricing financial assets, in understanding the Student’s t-distribution, in statistical inference, and in analysis of data.
. This work has value in pricing financial assets, in understanding the Student’s t-distribution, in statistical inference, and in analysis of data.
1. Introduction
A Student’s t-distribution is used for statistical inference for small sample sizes [1,2]. Nadarajah [3] states that the Student’s t-distribution is the second most popular distribution, second in popularity only to the normal distribution.
In addition to statistical inference, the Student’s t-distribution has application in finance, wherein the t-distribution is found to fit the distribution of the logarithms of daily returns better than a normal distribution or indeed better than most any other distribution [4-9]. The number of degrees of freedom, ![]() , is found by least squares fitting to historical returns to be around 3 for daily returns of the DJIA and S&P 500 indices [9], with increasing
, is found by least squares fitting to historical returns to be around 3 for daily returns of the DJIA and S&P 500 indices [9], with increasing ![]() for n-day returns,
for n-day returns, .
.
The Student’s t-distribution also has application wherever a Cauchy (Lorentzian) distribution is employed, since a Student’s t-distribution with one degree of freedom is a Cauchy distribution.
The Student’s t-distribution offers support from  to
to ![]() and has tails that decrease as
and has tails that decrease as  for
for . This causes problems in finance as integrals needed to price financial instruments diverge for the logarithm of returns distributed as a Student’s t-distribution [9-11] and the frequency of occurrence of the logarithms of daily returns is fit well by Student’s t-distribution.
. This causes problems in finance as integrals needed to price financial instruments diverge for the logarithm of returns distributed as a Student’s t-distribution [9-11] and the frequency of occurrence of the logarithms of daily returns is fit well by Student’s t-distribution.
Truncation, capping, and modification of the t-distribution have been put forth as means to deal with the divergence [8,9,12]. Moriconi [8] multiplied the Student’s t-distribution by an exp to keep integrals finite in pricing options. Lim et al. [12] used a generalized t-distribution [13], which has a multiplicative term of exp
to keep integrals finite in pricing options. Lim et al. [12] used a generalized t-distribution [13], which has a multiplicative term of exp . Lim et al. [12] reported that the generalized t-distribution fit currency options better than any other probability density function (pdf) that was used. The results presented here provide a physical basis for understanding the origin of a multiplicative factor.
. Lim et al. [12] reported that the generalized t-distribution fit currency options better than any other probability density function (pdf) that was used. The results presented here provide a physical basis for understanding the origin of a multiplicative factor.
Praetz [4] and Gerig et al. [7] pointed out that a Student’s t-distribution is obtained from a mixture of a normal distribution with a standard deviation ![]() that is distributed as an inverse chi distribution. If the support for the inverse chi distribution is taken to be zero to infinity, then a Student’s t-distribution is obtained from the mixture. For convenience, in this paper the reciprocal of
that is distributed as an inverse chi distribution. If the support for the inverse chi distribution is taken to be zero to infinity, then a Student’s t-distribution is obtained from the mixture. For convenience, in this paper the reciprocal of ![]() is denoted as
is denoted as![]() ,
,  , and
, and ![]() is distributed as chi,
is distributed as chi, :
:
 (1)
(1)
Using chi as defined above and a normal distribution with zero mean and standard deviation of , the mixing integral, when evaluated from
, the mixing integral, when evaluated from  to
to  yields a Student’s t-distribution
yields a Student’s t-distribution
 (2)
(2)
with a mean of zero, ![]() degrees of freedom, and a scale parameter of
degrees of freedom, and a scale parameter of . The parameters for the chi distribution were chosen to yield a Student’s t-distribution,
. The parameters for the chi distribution were chosen to yield a Student’s t-distribution,  , with a mean of zero,
, with a mean of zero, ![]() degrees of freedom, and a scale parameter of
degrees of freedom, and a scale parameter of .
.
If a chi distribution for the reciprocal of ![]() is left truncated, then the result of the mixing integral with the left-truncated chi distribution is a t-like distribution that has exponentially decaying tails. This result is demonstrated for
is left truncated, then the result of the mixing integral with the left-truncated chi distribution is a t-like distribution that has exponentially decaying tails. This result is demonstrated for . The integrals involved can be evaluated analytically for odd
. The integrals involved can be evaluated analytically for odd![]() . Small values of
. Small values of ![]() are of interest.
are of interest.
The contribution to a  Student’s t-distribution,
Student’s t-distribution,  , from values in the left-hand wing of the chi distribution for
, from values in the left-hand wing of the chi distribution for  is given by
is given by
 (3)
(3)
whereas the contribution from values in the right-hand wing of the chi distribution for  is given by
is given by
 (4)
(4)
It is interesting to note that the sum of the contributions from Equations (3) and (4) form a full Student’s t-distribution (in this case the mixing integral has been written as the sum of two exhaustive and exclusive regions:  and
and ), and that the right-hand contribution has an exponentially decaying tail. As a result, any pdf that does not include the left-hand contribution from the chi distribution for the reciprocal of the standard deviation in a chi-normal mixture will have tails that decay as exp
), and that the right-hand contribution has an exponentially decaying tail. As a result, any pdf that does not include the left-hand contribution from the chi distribution for the reciprocal of the standard deviation in a chi-normal mixture will have tails that decay as exp .
.
Figure 1 is a plot of a Student’s t-distribution with  degrees of freedom and the contributions to the t-distribution from the right-hand wing of the chi distribution and from the left-hand wing of the chi dis-
degrees of freedom and the contributions to the t-distribution from the right-hand wing of the chi distribution and from the left-hand wing of the chi dis-

Figure 1. Semi-log plots of a Student’s t-distribution with v = 3 and scale parameter β = 1 and of the contributions to the t-distribution from the leftand right-hand wings of the chi distribution in the chi-normal mixture that produces the Student’s t-distribution.
tribution. Figure 1 clearly shows that large values of the standard deviation ![]() in the mixture give rise to the fat tails of the t-distribution. The large values of the standard deviation occur for small values of the reciprocal of the standard deviation. For Figure 1, the wing of the chi distribution was truncated for an area of 0.01 in the wing. The small values of the standard deviation (large reciprocal; right wing) make a negligible contribution to the value of the Student’s t-distribution. The long tic mark at
in the mixture give rise to the fat tails of the t-distribution. The large values of the standard deviation occur for small values of the reciprocal of the standard deviation. For Figure 1, the wing of the chi distribution was truncated for an area of 0.01 in the wing. The small values of the standard deviation (large reciprocal; right wing) make a negligible contribution to the value of the Student’s t-distribution. The long tic mark at  marks the point where the area in each tail of the Student’s t-distribution equals 0.005, for a total area of 0.01.
marks the point where the area in each tail of the Student’s t-distribution equals 0.005, for a total area of 0.01.
The slowly decaying power tails of the t-distribution with increasing t results in the divergence of moments and of integrals required to price financial instruments that are based on a log Student’s t-distribution. The results presented in Figure 1 are interesting on two levels. One level is intrinsic interest in understanding the Student’s t-distribution and the other level is use. The results show the origins of the slowly decaying power tails of Student’s t-distributions and suggest an approach to deal with the divergence of moments and integrals based on the t-distribution.
Left truncation of the chi distribution for the reciprocal of the standard deviation to allow for only physically possible values of the standard deviation ![]() will impart exponentially decaying tails to the resulting t-like distribution from the chi-normal mixture. It is unlikely that
will impart exponentially decaying tails to the resulting t-like distribution from the chi-normal mixture. It is unlikely that . A value of
. A value of  implies no variability and a value of
implies no variability and a value of ![]() implies infinite variability.
implies infinite variability.
In the following sections, expressions for the probability density function (pdf), the variance, and the kurtosis are given for several small values of ![]() for t-like distributions that are obtained by left truncation of a chinormal mixture. In addition, the first several terms for power series expansions of the variance and kurtosis are given. These power series demonstrate the effect of the left truncation on the moments. Since the power series are valid only for small amounts of truncation, Figure 2 is presented. This figure shows the magnitude of the parameters involved for a left truncation of the chi distribution,
for t-like distributions that are obtained by left truncation of a chinormal mixture. In addition, the first several terms for power series expansions of the variance and kurtosis are given. These power series demonstrate the effect of the left truncation on the moments. Since the power series are valid only for small amounts of truncation, Figure 2 is presented. This figure shows the magnitude of the parameters involved for a left truncation of the chi distribution, . After Figure 2, some general definitions are given.
. After Figure 2, some general definitions are given.
Figure 2 plots the cumulative density function (CDF)
 for small values of the independent variable
for small values of the independent variable ![]() for the chi distribution in the mixing integral that yields a Student’s t-distribution with v = 1, 2, 3, 5 and 9 degrees of freedom. The long tic marks give the values (q = 0.0125, 0.10, 0.196, 0.333, 0.482) for which the CDF
for the chi distribution in the mixing integral that yields a Student’s t-distribution with v = 1, 2, 3, 5 and 9 degrees of freedom. The long tic marks give the values (q = 0.0125, 0.10, 0.196, 0.333, 0.482) for which the CDF . Figure 2 allows an appreciation of the differences amongst the chi distributions for different degrees of freedom and of the magnitudes of the numbers involved.
. Figure 2 allows an appreciation of the differences amongst the chi distributions for different degrees of freedom and of the magnitudes of the numbers involved.
The probability that ,
,  , is needed to normalize properly a truncated chi distribution. A left-truncated chi distribution
, is needed to normalize properly a truncated chi distribution. A left-truncated chi distribution  is zero for values
is zero for values :
:
 (5)
(5)
 is the pdf for a mixture of a left-truncated chi and normal distribution. If
is the pdf for a mixture of a left-truncated chi and normal distribution. If  then
then  would be a Student’s t-distribution with
would be a Student’s t-distribution with ![]() degrees of freedom and scale parameter
degrees of freedom and scale parameter . An explicit expression for
. An explicit expression for  is
is
 (6)
(6)
 is the variance of the pdf
is the variance of the pdf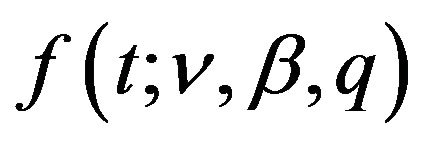 ,
,
 (7)
(7)
and  is the kurtosis of the pdf
is the kurtosis of the pdf ,
,
 (8)
(8)
This paper provides information on the effective truncation of a Student’s t-like distribution when the chi distribution for the reciprocal of the standard deviation is left-truncated. It is shown that the tails of the effectively truncated t-distribution go as exp . The contribution
. The contribution  to an odd
to an odd ![]() Student’s t-distribution from values of
Student’s t-distribution from values of  for a chi-normal mixture, i.e., Equation (4) evaluated for odd
for a chi-normal mixture, i.e., Equation (4) evaluated for odd![]() , is given by (see Equation (9) below).
, is given by (see Equation (9) below).

Figure 2. Plot of ![]() for small values of x and for v = 1, 2, 3, 5 and 9. The long tic marks on the abscissa mark the values for which the area to the left equals 1%, i.e.,
for small values of x and for v = 1, 2, 3, 5 and 9. The long tic marks on the abscissa mark the values for which the area to the left equals 1%, i.e., .
.
The expression, which decreases with t as exp , was obtained from an examination of the expressions for
, was obtained from an examination of the expressions for  for
for  and by comparison with the general case for odd
and by comparison with the general case for odd![]() . Clearly, left truncation of the chi distribution for the reciprocal of the standard deviation in a chi-normal mixture removes the fat tails of the Student’s t-distribution.
. Clearly, left truncation of the chi distribution for the reciprocal of the standard deviation in a chi-normal mixture removes the fat tails of the Student’s t-distribution.
2. Results
Expressions for some of the low![]() , effectively truncated Student’s t-distributions and moments are given in the following subsections. For a Student’s t-distribution the variance equals
, effectively truncated Student’s t-distributions and moments are given in the following subsections. For a Student’s t-distribution the variance equals  and exists only for
and exists only for . The kurtosis equals
. The kurtosis equals  and exists only for
and exists only for . For effectively truncated Student’s t-distributions (i.e., truncation of the large values of the standard deviation in the chi mixing distribution), the moments exist for all
. For effectively truncated Student’s t-distributions (i.e., truncation of the large values of the standard deviation in the chi mixing distribution), the moments exist for all![]() .
.
2.1. v = 1 (Cauchy or Lorentzian Distribution)
The pdf for a mixture of a left-truncated chi distribution for  and
and  and a normal distribution is
and a normal distribution is
 (10)
(10)
The tails of the pdf decrease as exp for non-zero
for non-zero .
.
 (9)
(9)
The first moment for  exists for the effectively truncated
exists for the effectively truncated  t-distribution and is given by
t-distribution and is given by
 (11)
(11)
where  is Euler’s contant and Ei() is the exponential integral. The series expansion is valid for
is Euler’s contant and Ei() is the exponential integral. The series expansion is valid for . The series expansion shows a logarithmic divergence as
. The series expansion shows a logarithmic divergence as  approaches zero, as expected for a Cauchy distribution.
approaches zero, as expected for a Cauchy distribution.
The  variance is given by
variance is given by
 (12)
(12)
is proportional to , remains finite for
, remains finite for , and diverges as
, and diverges as  as
as  approaches zero.
approaches zero.
An exact expression for the  kurtosis can be found, but the expression is long and cumbersome. The series expansion
kurtosis can be found, but the expression is long and cumbersome. The series expansion
 (13)
(13)
shows that the  kurtosis is proportional to
kurtosis is proportional to  and hence stays finite for
and hence stays finite for . Both the variance and the kurtosis are not defined for a Cauchy distribution, i.e., for a Student’s t-distribution with
. Both the variance and the kurtosis are not defined for a Cauchy distribution, i.e., for a Student’s t-distribution with  and a region of support from
and a region of support from  to
to![]() .
.
2.2. v = 2
The pdf,  , for a mixture of a left-truncated chi distribution for
, for a mixture of a left-truncated chi distribution for  and
and  with a normal pdf is
with a normal pdf is
 (14)
(14)
The first term in the series expansion is equal to .
.
 has tails that decrease as exp
has tails that decrease as exp for non-zero
for non-zero , since
, since  for large x. For large qt,
for large x. For large qt,
 (15)
(15)
Simple, analytic expression for the moments for even values of v could not be found.
2.3. v = 3
The  pdf,
pdf,  , equals
, equals
 (16)
(16)
and has tails that decrease as exp for non-zero q.
for non-zero q.
The  variance is given by
variance is given by
 (17)
(17)
and approaches  as q approaches zero. This is expected since the variance for a Student’s t-distribution exists for
as q approaches zero. This is expected since the variance for a Student’s t-distribution exists for  and equals
and equals  or
or  for v = 3.
for v = 3.
A series expansion for the  kurtosis (the exact expression is long and cumbersome) is
kurtosis (the exact expression is long and cumbersome) is
 (18)
(18)
and diverges as  as q approaches zero. The kurtosis for a Student’s t-distribution is defined only for
as q approaches zero. The kurtosis for a Student’s t-distribution is defined only for .
.
2.4. v = 5
The series expansion for the  variance shows a weak dependence on the left truncation. To lowest order in q, the
variance shows a weak dependence on the left truncation. To lowest order in q, the  variance has a cubic dependence on q. The curves of Figure 2 show that the chi distribution has decreasing area in the left for small q as v increases.
variance has a cubic dependence on q. The curves of Figure 2 show that the chi distribution has decreasing area in the left for small q as v increases.
 (19)
(19)
The series expansions for the  kurtosis is given by
kurtosis is given by
 (20)
(20)
The  kurtosis is finite for
kurtosis is finite for . The series expansion is a linear decrease in q for small q.
. The series expansion is a linear decrease in q for small q.
For , the first two terms of the alternating series for the expansion of the kurtosis are
, the first two terms of the alternating series for the expansion of the kurtosis are . For
. For  the kurtosis is not impacted by a truncation for small
the kurtosis is not impacted by a truncation for small .
.
3. Application
Application of the effectively truncated Student’s t-distribution to pricing a European call option is given in this section.
The value of a European call option at the time of expiration,  , is the expectation of the maximum value of
, is the expectation of the maximum value of ,
,  , where
, where  is the price of a stock at time T,
is the price of a stock at time T,  is the strike price at time T, T is the time when the option expires, and
is the strike price at time T, T is the time when the option expires, and  is the expectation operator [9]. It is not necessary to solve a partial differential equation to find the price of an option [9-11]. The desired quantity
is the expectation operator [9]. It is not necessary to solve a partial differential equation to find the price of an option [9-11]. The desired quantity , which is the value of the option at time
, which is the value of the option at time , is obtained from the expected time value of money. If
, is obtained from the expected time value of money. If ![]() is the risk free rate as a function of time t, then
is the risk free rate as a function of time t, then  when the risk free rate is assumed to be time independent. This is a standard assumption in the derivation of the Black-Scholes formula.
when the risk free rate is assumed to be time independent. This is a standard assumption in the derivation of the Black-Scholes formula.
Let  be the value of the stock at time T where
be the value of the stock at time T where  is a random variable, and where both
is a random variable, and where both  and the volatility
and the volatility  do not depend on the random variable
do not depend on the random variable .
.
In terms of the pdf for ,
,  , the value of the option at time T is
, the value of the option at time T is
 (21)
(21)
The value of  is determined by the requirements that the process be fair (i.e., the process is a martingale) and that the development in time of the price include the time value of money [9]. This requires that
is determined by the requirements that the process be fair (i.e., the process is a martingale) and that the development in time of the price include the time value of money [9]. This requires that
 where
where  is the value of the stock at time 0.
is the value of the stock at time 0.
If  is normally distributed, then
is normally distributed, then  follows a log normal distribution,
follows a log normal distribution,  , and the price for the option is given by the Black-Scholes formula.
, and the price for the option is given by the Black-Scholes formula.
If  follows a Student’s t-distribution, then
follows a Student’s t-distribution, then  is infinite. The exponential growth of
is infinite. The exponential growth of  with
with  dominates the
dominates the  tails of the Student’s distribution, Equation (2). However, if an effectively truncated Student’s t-distribution is used, then the tails of the effectively truncated t-distribution diminish with
tails of the Student’s distribution, Equation (2). However, if an effectively truncated Student’s t-distribution is used, then the tails of the effectively truncated t-distribution diminish with  as
as , and the value of the European call option remains finite. Both the effectively truncated Student’s t-distribution and the normal distribution have a multiplicative
, and the value of the European call option remains finite. Both the effectively truncated Student’s t-distribution and the normal distribution have a multiplicative  factor that dominates the exponential growth of
factor that dominates the exponential growth of  for large
for large . In general, the integral to price the European call option must be evaluated numerically. Equation (21) is perhaps the simplest manner in which to write the cost of the call option.
. In general, the integral to price the European call option must be evaluated numerically. Equation (21) is perhaps the simplest manner in which to write the cost of the call option.
The Student’s t-distribution is found (over the subinterval of the infinite region of support where returns are observed) to fit the distribution of the logarithms of daily returns better than a normal distribution or indeed better than most any other distribution [4-9]. It would be prudent to price options using a distribution that matches the data. The effectively truncated t-distribution that is described in this paper is a distribution that matches the observed data, as demonstrated in Figure 3.
Adaptive bins widths were used to generate the frequency of occurrence data for Figure 3. The bin width was increased until at least 5 counts were obtained in the bin. The normal distribution fits the data well only in the neighbourhood of  and does not fit the fat tails of the data. The quality of the fit of a Student’s t-distribution to the 15 491 data points that constitute the frequency of occurrence of ranges of values for the logarithms of the daily returns is remarkably good over all the returns, including the infrequent, low-probability events in the tails.
and does not fit the fat tails of the data. The quality of the fit of a Student’s t-distribution to the 15 491 data points that constitute the frequency of occurrence of ranges of values for the logarithms of the daily returns is remarkably good over all the returns, including the infrequent, low-probability events in the tails.
A fit of a Student’s t-distribution to the logarithm of the daily returns over the period of January 1950 to 27 July 2011 for the S&P 500 Index gives  and a scale parameter
and a scale parameter . The data show a kurtosis of 25 and a maximum 22-day volatility of
. The data show a kurtosis of 25 and a maximum 22-day volatility of . The approximation for the kurtosis for a
. The approximation for the kurtosis for a  effectively truncated t-distribution equal to 25,
effectively truncated t-distribution equal to 25,  , is solved for
, is solved for . The chi distribution in the mixing integral is, assuming that
. The chi distribution in the mixing integral is, assuming that , truncated for volatilities
, truncated for volatilities  to obtain the same kurtosis as the data. This level of truncation is roughly twice the maximum 22-day volatility of
to obtain the same kurtosis as the data. This level of truncation is roughly twice the maximum 22-day volatility of  that was obtained from the daily returns. Note that the kurtosis exists only for
that was obtained from the daily returns. Note that the kurtosis exists only for  for Student’s tdistributions. In contrast, the kurtosis is defined for
for Student’s tdistributions. In contrast, the kurtosis is defined for  for an effectively truncated t-distribution, in agreement with the data.
for an effectively truncated t-distribution, in agreement with the data.
The area in the left wing for truncation of the chi distribution at  to match the kurtosis of the observed daily returns of 25 is
to match the kurtosis of the observed daily returns of 25 is . This level of truncation of the chi distribution has a minor effect on the effectively truncated Student’s t-distribution for
. This level of truncation of the chi distribution has a minor effect on the effectively truncated Student’s t-distribution for , as can be observed in Figure 4. This is consistent with the data; all 15 491 data points lie in the interval −0.205 to +0.116. When the scale parameter
, as can be observed in Figure 4. This is consistent with the data; all 15 491 data points lie in the interval −0.205 to +0.116. When the scale parameter  is taken into account, the data lie in the region
is taken into account, the data lie in the region  The truncation to match the kurtosis is not severe (c.f. Figure 4), but the truncation is sufficient to keep finite the integrals required to price options with a log Student’s t-distribution.
The truncation to match the kurtosis is not severe (c.f. Figure 4), but the truncation is sufficient to keep finite the integrals required to price options with a log Student’s t-distribution.
4. Conclusions
A Student’s t-distribution arises from an averaging over the standard deviation of a normal distribution when the reciprocal of the standard deviation is distributed as chi. The Student’s t-distribution offers support over  to
to![]() . The slowly decaying power tails and infinite support region mean some moments for the Student’s t-distribution do not exist. This divergence of integrals
. The slowly decaying power tails and infinite support region mean some moments for the Student’s t-distribution do not exist. This divergence of integrals

Figure 3. Plots of the best fit Student’s t-distribution and normal distribution to the frequency of occurrence of the logarithms of daily returns for the S&P 500 index. The Student’s t-distribution fits the data well.

Figure 4. Plot of a v = 3 Student’s t-distribution (red) and an effectively truncated v = 3 Student’s t-distribution (green). The truncation was chosen to match the observed kurtosis of the daily returns for the S&P 500 index over the period of January 1950 to 27 July 2011.
can cause problems, particularly in the pricing of options where the logarithm of returns is distributed as a Student’s t-distribution. One approach to deal with the divergence is to truncate the Student’s t-distribution [9]. Data typically fit well to the central region of the t-distribution and are nonexistent far from the central region of the Student’s t-distribution. Other approaches are to multiply the t-distribution by an envelope function that reduces the impact of the tails [8] or to use a generalized form that includes an envelope function that reduces the impact of the tails [12]. The approach presented here is to left-truncate a chi distribution for the reciprocal of the standard deviation. The chi distribution is used in a mixing integral with a normal distribution to yield an effectively truncated Student’s t-distribution. Left truncation of the chi distribution at q yields tails for the effectively truncated Student’s t-distribution that decay with increasing t as . The approach adopted here supports the envelope multiplication of Moriconi [8] by showing that the envelope modification is similar in effect to a left truncation of a chi distribution for the reciprocal of the standard deviation, and then mixing the truncated chi distribution with a normal distribution of the same standard deviation.
. The approach adopted here supports the envelope multiplication of Moriconi [8] by showing that the envelope modification is similar in effect to a left truncation of a chi distribution for the reciprocal of the standard deviation, and then mixing the truncated chi distribution with a normal distribution of the same standard deviation.
Expressions or power series expressions for the pdf, variance, and kurtosis for several low number of degrees of freedom, effectively truncated Student’s t-distributions are given. These expressions demonstrate the exponential tails of the effectively truncated t-distribution and show that the variance and kurtosis remain remain finite for the effectively truncated distributions. In addition, it is shown that it is the large values of the standard deviation in the mixing integral that give rise to the fat tails of the Student’s t-distribution. The small values of the standard deviation in the mixing integral do not contribute to the tails of the Student’s t-distribution and only weakly contribute to the core of the Student’s t-distribution.
The effective truncation of the Student’s t-distribution means that integrals required to price financial instruments such as European call options remain finite. This permits pricing with a distribution, the log Student’s t-distribution, that describes well returns for stocks.
Simple expressions were not found for the effectively truncated t-distributions with even numbers of degrees of freedom. Given the importance of the Student’s t-distribution in the description of returns and data in general, it would be helpful to find accurate approximations that smoothly approach the expressions for the odd numbers of degrees of freedom. These approximations could then be used to model data where it is unphysical to assume support over  to
to![]() . The
. The  envelope modification of Moriconi [8] might be a sufficiently good approximation for all degrees of freedom. It is shown that the envelope modification of Moriconi is functionally equivalent to a truncation of large values of the volatility (standard deviation) in the chi distribution of the chi-normal mixing integral that leads to a Student’s t-distribution.
envelope modification of Moriconi [8] might be a sufficiently good approximation for all degrees of freedom. It is shown that the envelope modification of Moriconi is functionally equivalent to a truncation of large values of the volatility (standard deviation) in the chi distribution of the chi-normal mixing integral that leads to a Student’s t-distribution.
5. Acknowledgements
This work was funded by the Natural Science and Engineering Research Council (NSERC) Canada.
REFERENCES
- Student, “The Probable Error of a Mean,” Biometrika, Vol. 6, No. 1, 1908, pp. 1-25.
- S. L. Zabell, “On Student’s 1908 Article ‘The Probable Error of a Mean’,” Journal of the American Statistical Association, Vol. 103, No. 481, 2008, pp. 1-7. doi:10.1198/016214508000000030
- S. Nadarajah, “Explicit Expressions for Moments of t Order Statistic,” Comptes Rendus de l’Académie des Sciences—Series I, Vol. 345, No. 9, 2007, pp. 523-526. doi:10.1016/j.crma.2007.10.027
- P. D. Praetz, “The Distribution of Share Price Changes,” The Journal of Business, Vol. 45, No. 1, 1972, pp. 49-55. doi:10.1086/295425
- R. C. Blattberg and N. Gonedes, “A Comparison of the Stable and Student Distributions as Statistical Models for Stock Prices,” The Journal of Business, Vol. 47, No. 2, 1974, pp. 244-280. doi:10.1086/295634
- E. Platen and R. Sidorowicz, “Empirical Evidence on Student-t Log-Returns of Diversified World Stock Indices,” Research Paper 194, Quantitative Finance Research Centre, University of Technology, Sydney, 2007. http://www.business.uts.edu.au/qfrc/research/research_papers/rp194.pdf
- A. Gerig, J. Vicente and M. Fuentes, “Model for Non-Gaussian Intraday Stock Returns,” Physical Review E, Vol. 80, No. 6, 2009, pp. 1-4. doi:10.1103/PhysRevE.80.065102
- L. Moriconi, “Delta Hedged Option Valuation with Underlying Non-Gaussian Returns,” Physica A, Vol. 380, No. 1, 2007, pp. 343-350. doi:10.1016/j.physa.2007.01.018
- D. T. Cassidy, M. J. Hamp and R. Ouyed, “Pricing European Options with a Log Student’s t-Distribution: A Gosset Formula,” Physica A, Vol. 389, No. 24, 2010, pp. 5736- 5748. doi:10.1016/j.physa.2010.08.037
- J.-P. Bouchaud and D. Sornette, “The Black-Scholes Option Pricing Problem in Mathematical Finance: Generalization and Extensions for a Large Class of Stochastic Processes,” Journal de Physique I (France), Vol. 4, No. 6, 1994, pp. 863-881. doi:10.1051/jp1:1994233
- J. L. McCauley, G. H. Gunaratne and K. E. Bassler, “Martingale Option Pricing,” Physica A, Vol. 380, No. 1, 2007, pp. 351-356. doi:10.1016/j.physa.2007.02.038
- G. C. Lim, G. M. Martin and V. L. Martin, “Pricing Currency Options in the Presence of Time-Varying Volatility and Non-Normalities,” Journal of Multinational Financial Management, Vol. 16, No. 3, 2006, pp. 291-314. doi:10.1016/j.mulfin.2005.08.004
- J. N. Lye and V. L. Martin, “Robust Estimation, NonNormalities and Generalized Exponential Distributions,” Journal of the American Statistical Association, Vol. 88, No. 421, 1993, pp. 261-267. doi:10.2307/2290721

