Open Journal of Physical Chemistry
Vol.2 No.4(2012), Article ID:24981,9 pages DOI:10.4236/ojpc.2012.24034
Electron—Proton Twins, Orderly Arranged in the Inside of Bioatoms
1Institute of Biomedical Research & Biotechnology, Athens, Greece
2Department of Mechanical Engineering, Laboratory of Applied Thermodynamics, Polytechnic School of Thessaloniki, Thessaloniki, Greece
Email: sengir@ath.forthnet.gr
Received July 6, 2012; revised August 5, 2012; accepted September 7, 2012
Keywords: Bioatoms; Proton Network; Ionisation Energy; Helium
ABSTRACT
In the present study the first 20 microatoms of the periodic table are named as bioatoms, since they are needed for biochemical functions and services to life itself. The rationale behind this project is the detailed analysis of the ionization energy of the electrons in the inside of the bioatoms and their orderly arrangement at specific positions. Such position of the electrons is harmonized with the succession of their energy values in their logarithmic curves. The compelling arrangement of each electron at a particular place would not be feasible in the absence of an energy offset, which is a proton. The latter would hold electrons on their proper position. These fundamental aspects of our project receive such strong support from the quantum theory, according to which it is the electromagnetic interaction between electrons and protons by the exchange of photons, which hold them together in the atoms. According to our proposed model, the protons of the aforementioned proton—electron twins, are distributed on distinct positions which are the junctions of a primary network, coupled with their electrons, in a secondary network. The geometry and distance of the protons, in the plexus, is constant and is calculated at 8, 42 Å. This was estimated by a mathematical analysis of the proposed model, as discussed further. Our study has shown that electrons in the specific positions are moving in a symmetrical oscillation in the length of a channel, in vacuum, under the Coulomb forces. Moreover, the chemical evidence suggests that electrons, in an atom, have their own separate orbit, and that these orbits are closely interrelated.
1. Introduction
The term “bioatom” is, for the first time, being used in the present study. Bioatoms are the original atoms (microatoms) of the periodic table, essential for biological activities. This new term lends itself to a distinction between the microatoms and the heavier atoms of the periodic table; In accordance with the existing knowledge concerning the origin of the atoms, the chemical elements are formed by a primary stellar nuclosynthesis, while the heavier components are born by the explosion of supernovae. If, according to Rutherford’s model [1,2], electrons are placed at specific locations around the nucleus of the atom, the stability of the atom’s structure presupposes an energy influence on each individual electron by an equal but opposite energy unit, which in the case in point is a proton. According to quantum theory, it is the electromagnetic interaction (by the exchange of photons) which holds electrons and nuclei (protons) together in the atoms [3]. But up till now quantum theory has never provided a practical model of how electrons and nuclei (protons) can absorb and emit photons [3]. This is because the completely successful application of the quantum theory to the atom structure has been limited to the hydrogen atom which disposes only one electron. There is, therefore, no certainty as to how this theory could be formulated for the case of a more complicated atom such as bioatoms. The interchange of photos, between electrons and protons, strengthens our point of view that all electrons, in their fixed position inside the electromagnetic field in the interior of the bioatoms are influenced equally by the same quantity of energy, due to protons. The magnetic properties of these subatomic elements furnish excellent proof of the electron coupling with protons.
Our proposal gives a concrete answer to this leading issue concerning the interrelationship between electrons and protons, by proving that protons and electrons participate mutually—by the exchange of photons—to the formation of twins, in a steady position and constant distance between them. The accuracy of this claim is affirmed by the quantity of the ionization energy necessary for the successive detachment of the electrons. Looking carefully at the absolute and logarithmic values of the successive ionization energies of electrons in different published papers [4-29] we can ascertain that in all atoms there are two central electrons that have ionization energy manifold greater as compared to the ionization energy of the rest of the peripheral electrons (Figure 1).
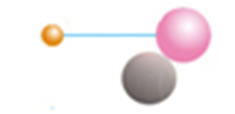
We suggest that these two electrons are not placed on a separate orbit but together with two protons and two neutrons form a helium atom placed at the centre of the atom (Figure 2(c)). For these two electrons we have estimated a progressive increase, in the values of the ionization energy for carbon to the calcium atom (Table 1). In order to study in detail these two interesting electrons we have scrutinized a possible attachment of a structure unit to a helium atom for its transition to another atom of different structure and different properties. A structure unit in this study is a new term, relevant to three sub- atomic particles: proton, electron and neutron, as a structural and functional entity (Figures 2(a) and (b)).
It appears that the structure units, during their attachment to helium atoms are placed in a mirror-image position, guided by Coulomb forces and form two networks:
The primary network, which consists of protons and neutrons and the secondary network which consists of electrons (Figure 3).
In our mathematical analysis we will show that the distance among protons and between protons and electrons are strictly equal, calculated at 8, 42 Å.
The exceptional upgrading accuracy of the values of the electron ionization energy in the literature as compared to the results of our new atomic structure for all electrons, especially for the two central electrons, shown in Table 2, is an extremely important finding as it substantiates the logic of the proposed new structure of bioatoms.
The attachment, for example, of a structure unit to a helium atom should be followed by the addition of certain quantity of energy which has been estimated in our study at 2.633 MJ·mol–1 for each of the two central electrons (Table 1). For the more peripheral eight electrons (octet of Landé) [30,31], there is also a need for the addition of a quantity of energy equal to 0.66 MJ·mol–1 for each electron (Figure 4).

Figure 1. Two electrons (indicated by arrows) have ionization energy manifold greater than the ionization energy of other electrons.
 (a)
(a)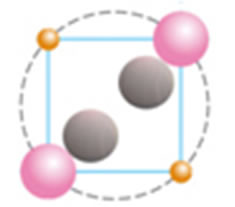 (b)
(b) (c)
(c)
Figure 2. (a) Structural unit; (b) Helium atom; (c) Calcium atom showing protons (pink), electrons (orange), neutrons (grey) and a helium atom at the center of the atom.

Table 1. Upgrading of the ionization energies of the two central (α1, α2) electrons from the carbon atom to the calcium atom (I.E.: Ionization Energy).
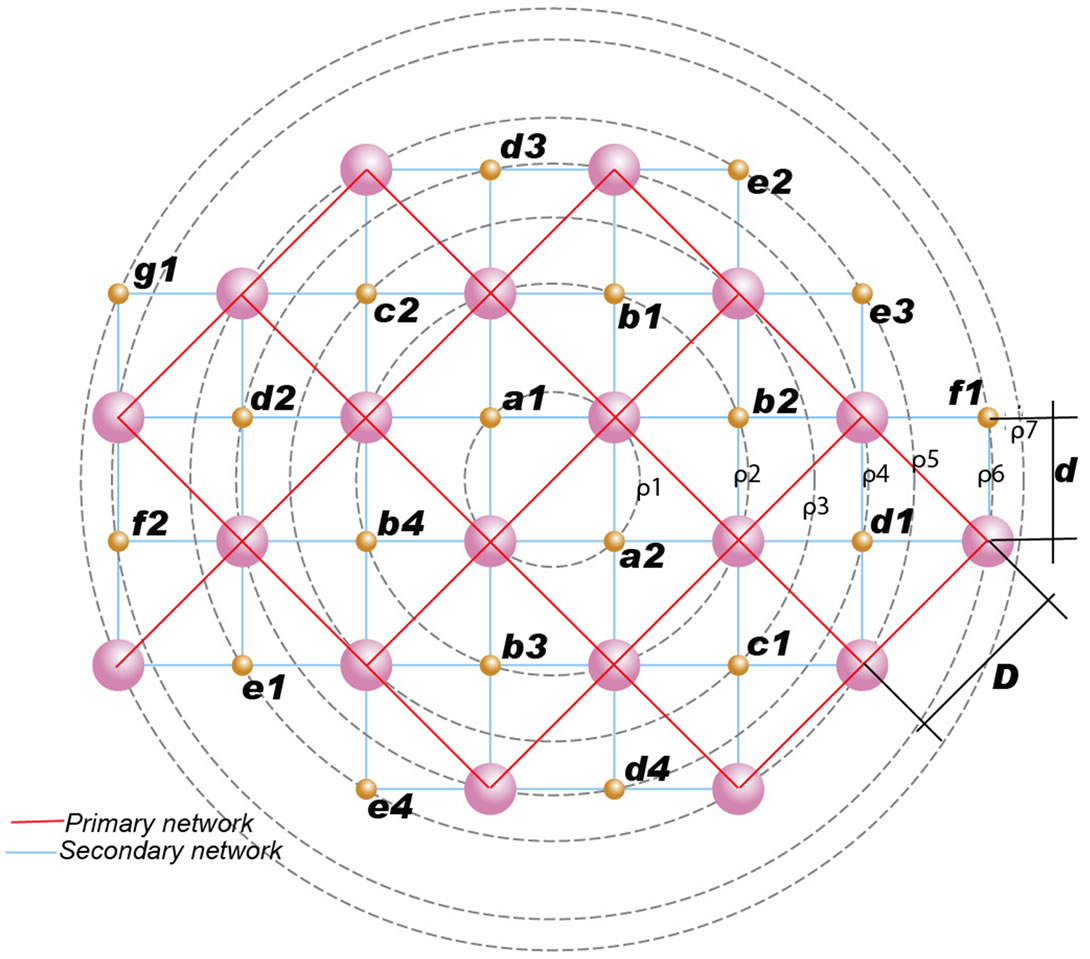
Figure 3. Primary and secondary network in a potassium atom.
For the most peripheral octet of electrons the quantity of energy for each electron is 0.33 MJ·mol–1.This energy arrangement shows that the quantity of energy for each specific electron is strictly graduated in proportion to the degree of influence they receive according to their position inside the energy field in which they reside. Quantum theory maintains that among electrons and protons there is an electromagnetic reaction (interchange of photons) which holds electrons and protons in a fixed position [3]. This couldn’t have happened by a central solitary energy nuclear “mass”, if electrons are placed at different distances from the nucleus. In order for each proton to influence equally each peripheral electron it should be placed at equal distance from it. Thus, the progressive structure of bioatoms presupposes an arrangement in fixed positions. This kind of structure in bioatoms is confirmed by the mode of upgrading the electron ionization energy from one atom to the next (Table 1).
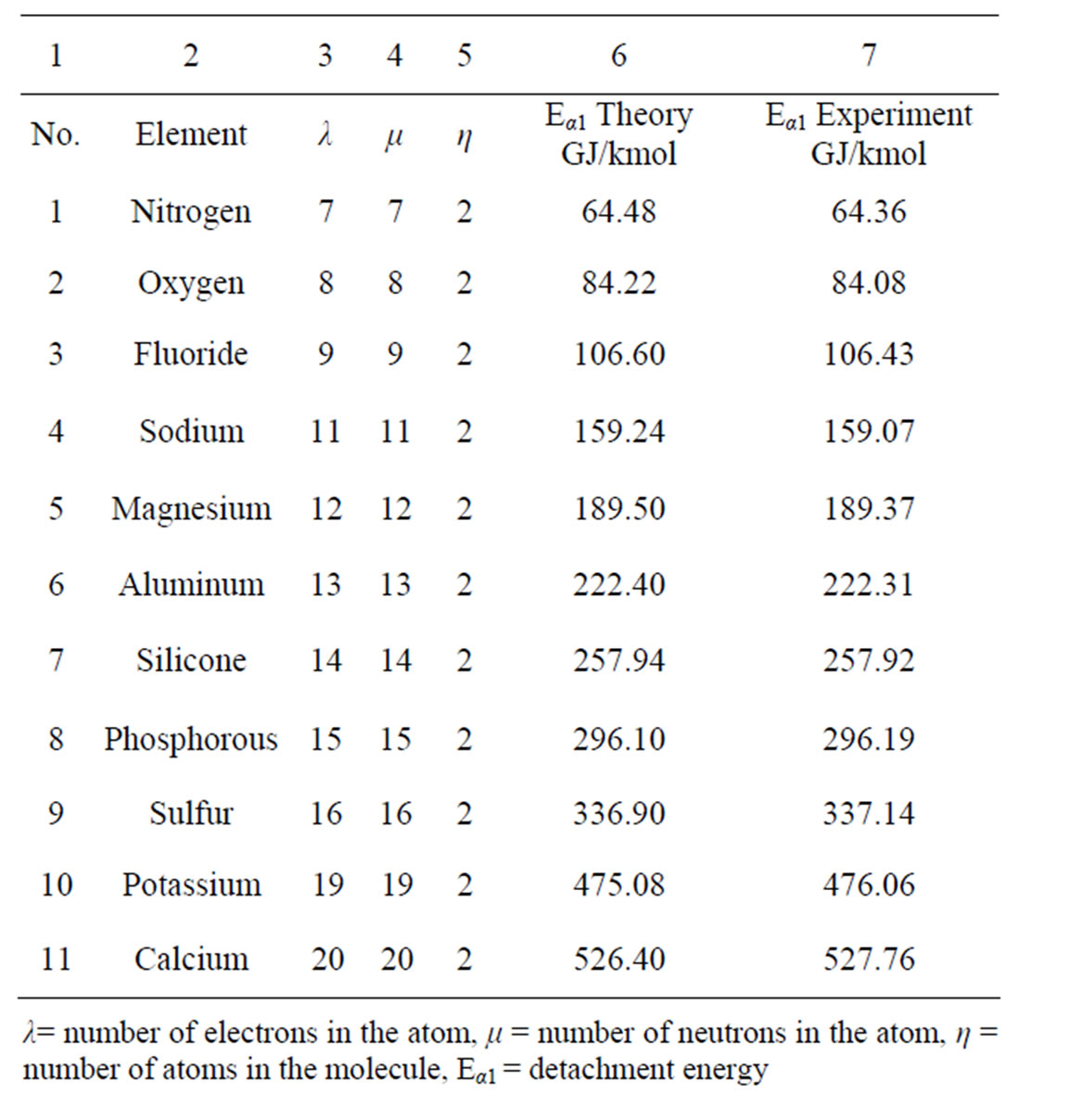
Table 2. Central electrons: exceptional accuracy of the values of their ionization energy in the literature as compared to the results of our study.
Such an arrangement of electrons and protons in space could be ensured only with the formation of twins, which in all, form the networks and contribute to the formation of the electromagnetic field.
The accuracy of the proposed model is affirmed by the quantity of the ionization energy, necessary for the successive detachment of the electrons. The harmonization of the electron detachment with the arrangement of the structure unit into the specially shaped energy field, both accommodate the equal interaction between electrons and protons and create the energy decay of the energy field from the centre of the atom to the peripheral orbit.
In our proposal, electrons move in symmetrical rectilinear oscillation in the length of the electromagnetic channel, in vacuum, under the influence of Coulomb forces (Figure 5).
The quantity of ionization energy needed for the detachment of each electron was estimated even on the basis of its oscillation amplitude (Table 3).
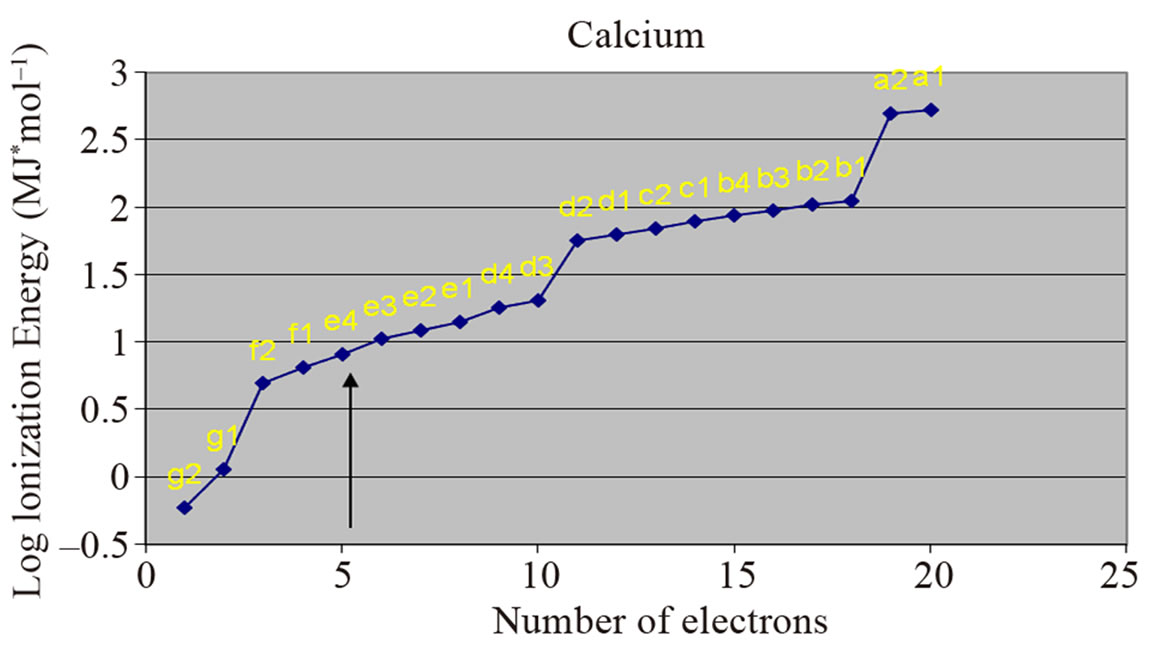
Figure 4. Grouping of electrons in octets (arrows).
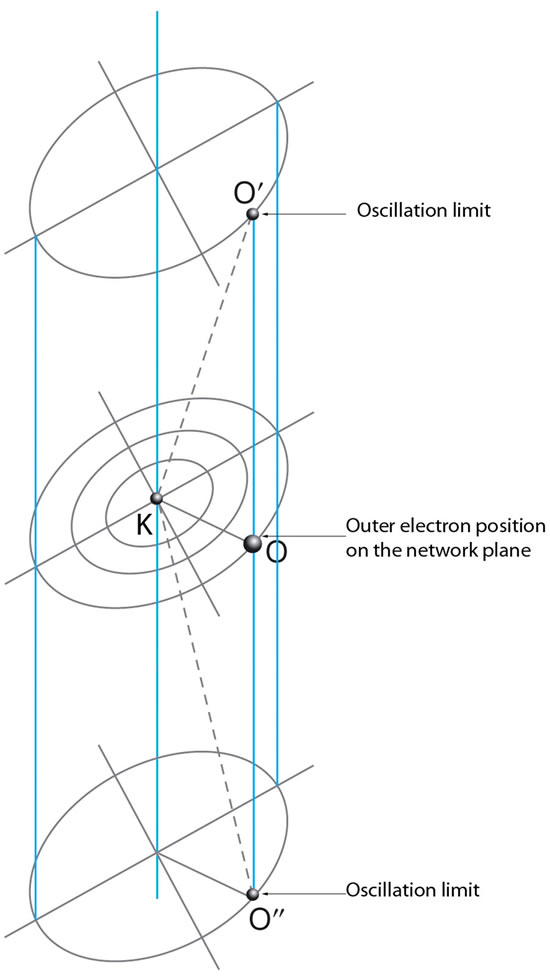
Figure 5. Electrons are in symmetrical oscillation in the length of a magnetic channel under the influence of Coulomb electric forces. The oscillation is not linear, therefore movement is not harmonic.
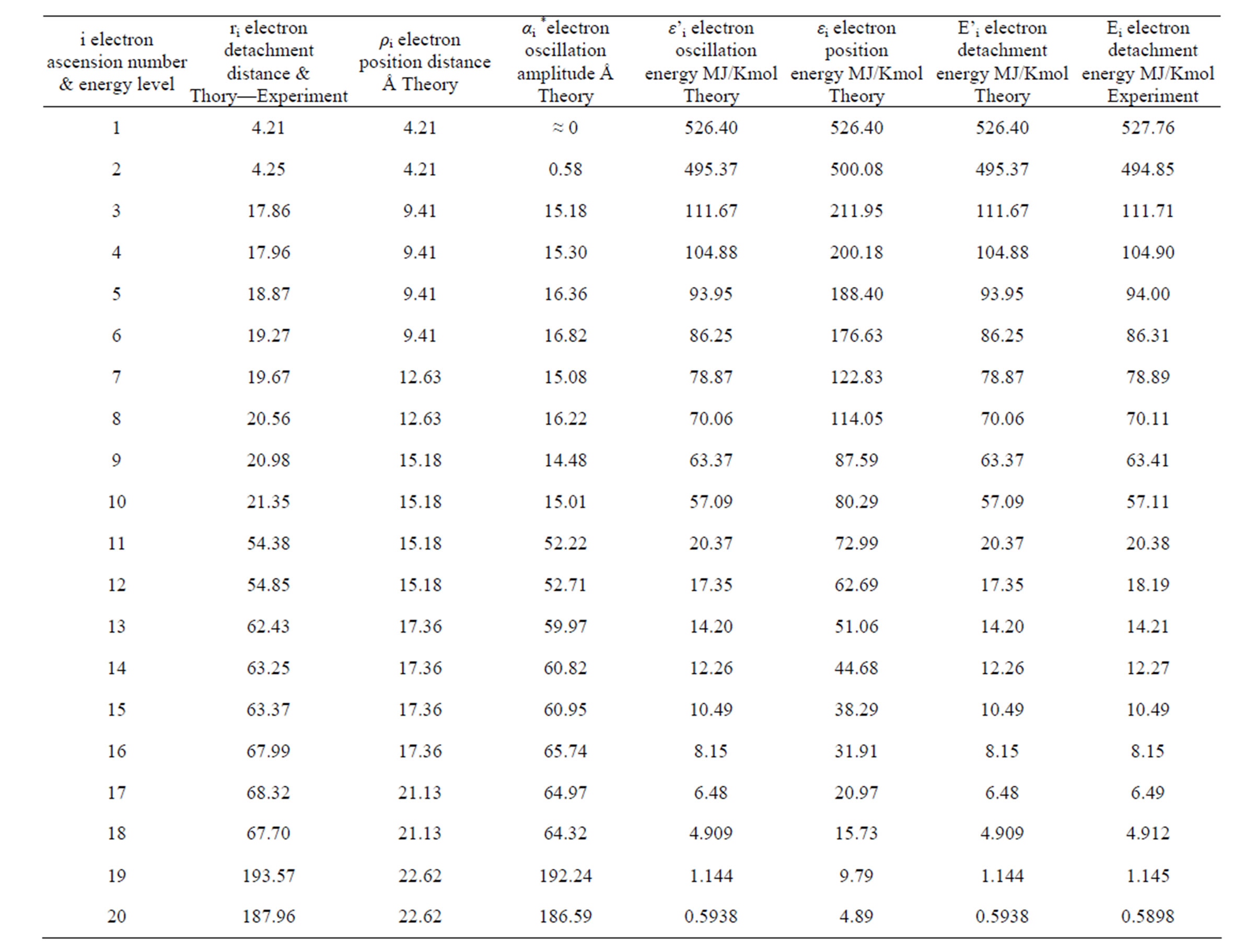
Table 3. Energies for each electron of the calcium atom.
The important role of the quantum theory in supporting our project is clear: Quantum theory attempts to determine the way through which electrons and protons form twins and hold each other by the exchange of photons.
Our contribution is the determination of the arrangement of the proton/electron twins in space, the distance between electrons and protons and the necessary energy to achieve the union between the twins. Furthermore, it should be pointed out that up till now little is known on the role of neutrons in the completion of the structure and function of bioatoms.
Neutrons being in the interior of the energy field of the atoms, lend distinctive characteristics to them. For example, the addition of a structure unit to the carbon atom (one proton, one electron and one neutron) creates a nitrogen atom. However the addition of a hydrogen atom (one proton, one electron) to the carbon atom creates a simple chemical bond (Figure 6).
This finding shows that neutrons play an extremely important role in the chemical and physical properties of bioatoms.
The mathematical process of the proposed model substantiates our claims concerning the space-arrangement of protons and electrons in the form of two networks, estimates the distance between protons and electrons and offers a stable structure to the atoms.
2. Experimental Approach of the Proposed Structure of The Atom
The geometrical sizes of protons, neutrons and electrons are assumed as of spherical shape. The sizes of their mass and electrical charge are known. The electrical
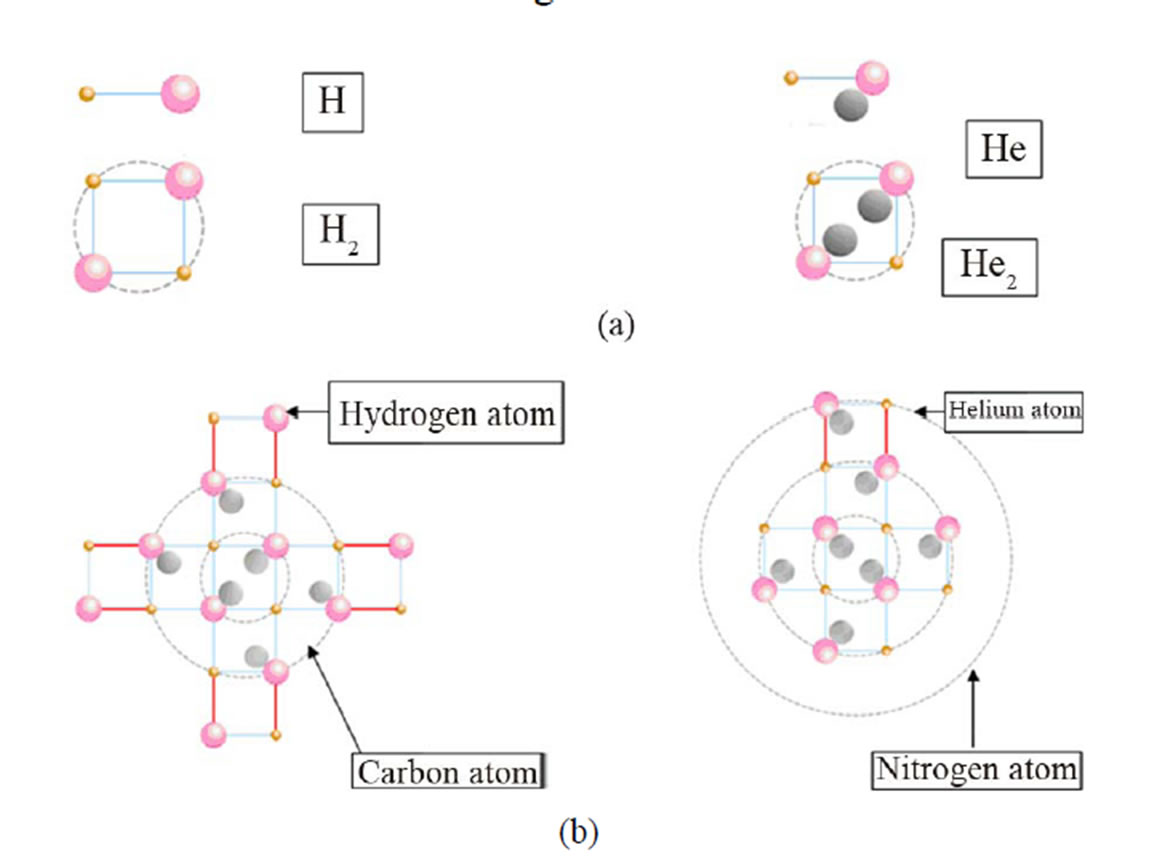
Figure 6. The addition of a structure unit to the carbon atom creates a nitrogen atom. The addition of a hydrogen atom to a carbon atom creates a simple chemical bond. H: Hydrogen atom, H2: Hydrogen molecule, He: structure unit, He2: helium atom.
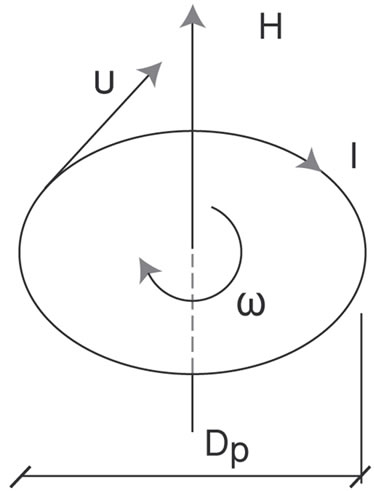
charge of protons is distributed on their maximum diameter Dp. Their distance D, as we shall prove, remains constant and depends only on the angular momentum (spin) of protons. The production of angular momentum from angular velocity ω and vice versa is obvious from Figure 7(a).
It is: Polar inertia torque θ (kgm2)
Proton angular momentum L = θω (Js)
Current due to spin I = eω (A)
Resulting magnetic field H = I/Dp
The conditions in the space of the atom are considered as conditions in vacuum, with a magnetic constant μο= 1.257 × 10–6 (Vs/Am) and dielectric constant εο= 8.854 × 10–12 (F/m).
Magnetic density is: B = μοΗ
Magnetic flow is: Φ = Bq Where q is the surface run through by flow Φ.
The magnetic circle of a nuclear dipole is:
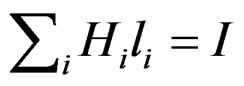
The attraction force of the dipoles’ protons due to flow Φ is:
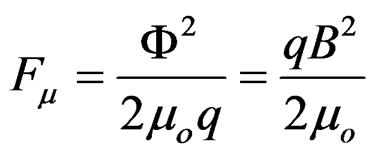 (Figure 7(b))
(Figure 7(b))
The principle of momentum conservation on the proton dipole in the closed integral in the whole circle Φ = constant.
Therefore:
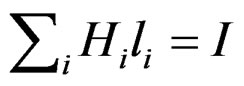
or
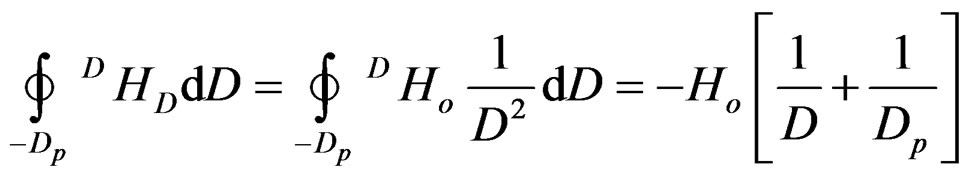
with Ho=2eω and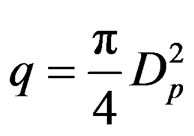 the attraction force at a distance D between them is:
the attraction force at a distance D between them is:
 (a)
(a)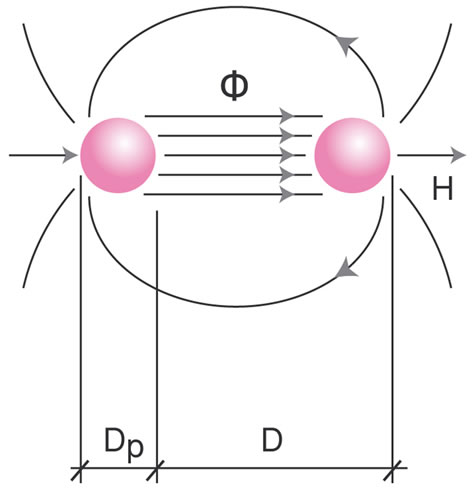 (b)
(b)
Figure 7. (a): Electromagnetic field due to angular momentum (u = angular velocity, ω = angular momentum, Dp = proton diameter, I = current, H = magnetic field); (b): Proton magnetic dipole (Φ = magnetic flow, H = magnetic field, Dp = proton diameter, D = proton distance).
 (1)
(1)
They are repulsed with a force Fe due to their positive charge based on Coulomb’s law.
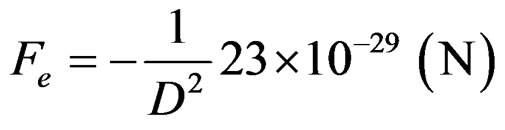 (2)
(2)
The balance between electrical and magnetic forces is achieved through
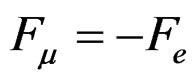 (3)
(3)
From (1), (2) and (3) the eliminant is derived
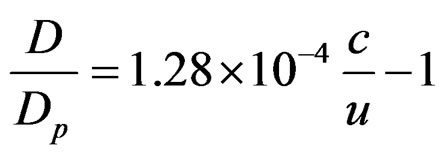 (4)
(4)
where: 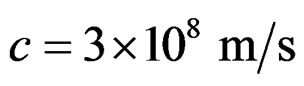 the speed of light and u (m/s) the tangent velocity of the proton.
the speed of light and u (m/s) the tangent velocity of the proton. 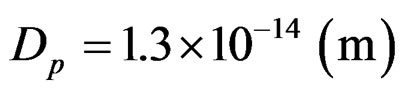 is the proton’s diameter.
is the proton’s diameter.
From (4) the following observations are derived:
• At an angular momentum with 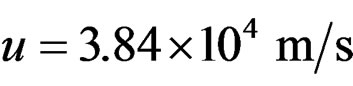 the two protons come together since D/Dp = 0 → D = 0
the two protons come together since D/Dp = 0 → D = 0
• At an angular momentum with 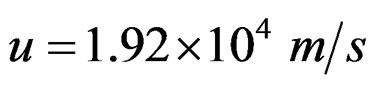 a rupture of Coulomb’s barrier occurs. Now the protons balance between them at a contact position.
a rupture of Coulomb’s barrier occurs. Now the protons balance between them at a contact position.
• At an angular momentum with velocities of the positive charges smaller than 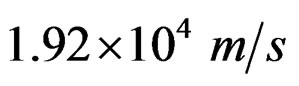 protons balance at a distance D which can be calculated by Equation (4).
protons balance at a distance D which can be calculated by Equation (4).
• The magnetic dipole of two or more protons does not depend on the measure of their positive charges, because Equation (4) involves only measures of velocity and dimensions. Therefore for any Q+ is D = constant. This means that the positive charge can also associate with other protons or electrons, without change in the distance between protons.
Following the above observations we conclude that the space arrangement and geometry of the atom/molecule according to Figure 7(c) is stable.
The denoted electrons of diameter De are attracted by the protons with diameter Dp. These forces give a resultant at the drawing level vertical to the flow of the magnetic field which also lies or is parallel to the drawing level. Therefore the exercised forces on the electrons are, as the external vectorial product of the latter, vertical to the drawing level. In this way the magnetic field creates a channel vertical to the drawing level for each electron. Hence the electrons are in a symmetric linear oscillation in the length of this channel under the influence of Coulomb electric forces.
The oscillation amplitude is defined by the electric potential for every specific system and for each electron. This is derived by the analysis of ionized atoms and is considered by the following, where the proton distance D is also defined.
Based on the value which derives from Equation (10), 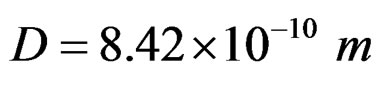 and from (4) we can define the protons’ tangent velocity of angular momentum:
and from (4) we can define the protons’ tangent velocity of angular momentum:
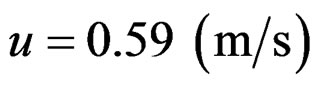
Angular momentum (spin) is calculated by L = θω
with the protons’ polar torque
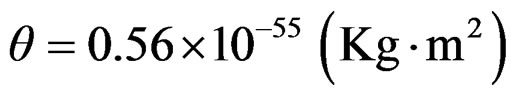
and angular velocity

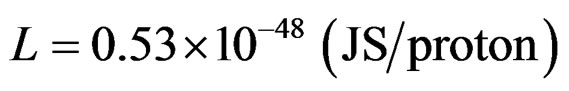
The above applies for all protons, at least for the elements that are incorporated in the context of this study.
2.1. Energy Analysis for The Bioatomic Structure
The analytical elaboration of the proposed model from an energy point of view, has taken into consideration the following:
• Protons together with neutrons are distributed on a network. The same applies for electrons which are on a secondary network.
• The distance of the junctions of the network does not change.
• Dynamic balances due to developing magnetic or electrical forces were not taken into account since the networks were considered firm.
• The attempted, in the following, energy analysis aims to define the geometric sizes through calculations of the electric potentials and their comparison with measurements established in current bibliography.
• It was assumed that in the distributed nucleus, the positive charges are concentrated at the centre of symmetry of the network which is occupied by a helium (He) molecule in all the elements.
• The appearing homocentric circles are part of the characteristics of the network. All the electrons are present at their peripheries and are affected by the positive charges of the centre of positive charges K.
The proposed bioatomic structure of the atom’s nucleus in all elements, for example the atom of calcium, can be seen in Figure 1(c). Protons and neutrons are at the junctions of the rectangular network at distances D. This is the primary network.
Electrons are located at the junctions of the diagonals of the primary network by dividing

which we characterize as secondary network.
The ratio of the radials of the circles as a geometric location of the junctions of the networks 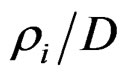 has the following values:
has the following values:
0.500/1.118/1.500/1.803/2.062/2.510/2.686/…
The spherical electric potential which resists the detachment of electrons is due to Coulomb forces, which in vacuum give:
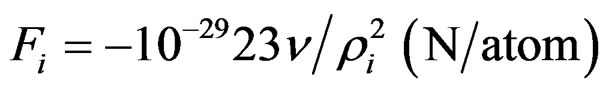 (5)
(5)
ρi (m) distance of electrons from the centre of positive charges
ν (–) number of positive charges that correspond to the detached electron.
The detachment energy of the i-electron can be calculated by the integral:
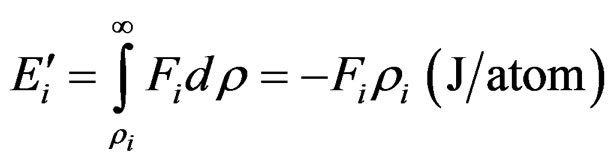 (6)
(6)
The energy 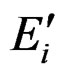 is independent of the escape path from ρi to ∞ of the electron.
is independent of the escape path from ρi to ∞ of the electron.
It is obvious for a substance atom with λ electrons the following applies:

with I = λ for the first valency electron of the outer orbital and I = 1 for the last electron of the inner orbital.
The above electron detachment energies from a substance atom are compared with values for detachment of electrons by ionization from the respective bibliography. Those for 11 elements are shown in Table 3, column 7 and refer to kmol of substance.
For the comparison (6) is transformed to:
 (7)
(7)
We observe that the values of column 7 in Table 1 are reflected with extreme accuracy by the relationship:
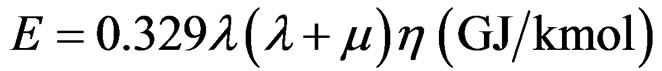 (8)
(8)
where: μ number of neutrons in the atom, η number of atoms in the molecule (single atoms are counted as dual atoms)
N Avogadro’s constant 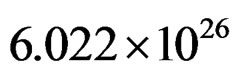 number of atoms/kmol Relationship (3) for the electron of the inner orbital with I = 1 can be written:
number of atoms/kmol Relationship (3) for the electron of the inner orbital with I = 1 can be written:
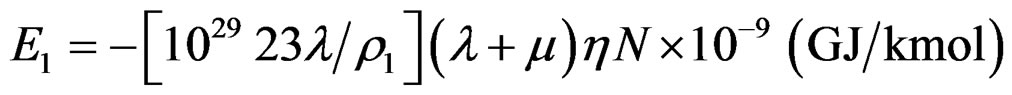 (9)
(9)
Because E = –E1 from (8) and (9) we can derive for all elements:
 (10)
(10)
This means that the distance between the junctions of the primary network of protons of the arranged nucleus according to the proposed bioatomic structure is constant, at least for all the elements that are under consideration in this analysis and are included in Table 1.
The values for the detachment of an electron of the inner orbital that are calculated by (9) are included in column 6 of Τable 3.
The extreme accuracy between theory and experiment (columns 6 and 7) is important for the required detachment energy of the last electron of all the elements that are referred in Τable 3.
With μ = λ and η = 2, something that occurs in all the substances in question, we derive through (8):
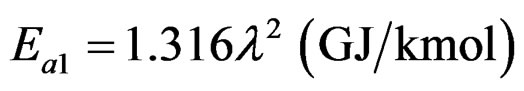 (11)
(11)
Relationships (8) and (9) constitute an analytical statement of the experimental measurements.
The detachment energy of the first valency electron of the outer orbital of the nucleus demands significantly less energy.
As it is derived by (11), the ratio between the maximum and minimum detachment energy of an electron is approximately equal to the square of the number of electrons of the atom of the element; in other words λ2.
The detailed calculation of detachment energy of all the electrons of an atom and its comparison with that measured by ionization, takes into account the oscillation of electrons and therefore the oscillation amplitude αi, apart from the distance ρi from the oscillation channel of electrons. Hence the distance ri that defines the outermost position of electrons from the centre of positive charges in the field of the spherical Coulomb potential is:
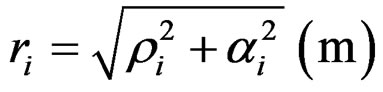 (12)
(12)
With the distances ρi and the oscillation amplitude αi we have calculated in Table 5 the required detachment energies for each electron of oxygen, as an example, and they were compared to the energies that have been derived experimentally. They came out:
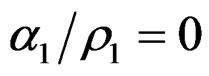 ,
, 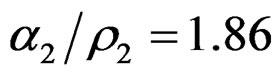 and
and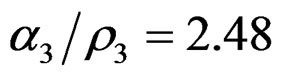 .
.
3. Conclusions
Our proposal is a timely reminder of the importance of the fundamental aspects of subatomic structure. Advances in the field in the past century have been considerable, and have resulted in multidisciplinary research [32-40]. The results of the present study enforce the association of the initial revolutional scientific thought of Rutherford [1,2] to the later stages of the quantum mechanics attempt to explain the stability of matter.
In the present study we went off in quest of the concrete space arrangement of the electrons and protons in bioatoms. We have also, formulated the quantitative and qualitative stability requirements for the bioatomic structure, namely the space arrangement of protons, electrons and neutrons, in a manner that: 1) can ensure a steady equilibrium and 2) confirm the relationship between energy and matter. These two parameters are extremely important.
As each electron and proton is charged with the same quantity of negative or positive energy—respectively— their interaction must equally be affected. In this case distances between them are to be equal and influence their interaction with the same intensity. This is not feasible if electrons are disorderly dispersed around a positively charged massive nucleus and not amenable to ordinary rules. Besides, it is not understandable how the structuring mechanism of the atoms could work properly with the electrons in disarray around the nucleus. This could show an unruly structure of the atoms since in the same time their energy condition shows an absolutely concrete and definite energy upgrading in the course of our structuring model, as shown in Table 1. Moreover, in our model a trinity of proton, electron and neutron is proposed as a structure unit, which justifies the existing order inside the atomic structure. Furthermore, the orderly structure in bioatoms, distinguishes for the first time the master role of the neutrons. The strictly definite energy upgrading of electrons during succession of one atom to the next, substantiates the existence of a structural order, which serves the stability of the proposed model and strengthens its rational.
In conformity with the ionization energy, the distance between protons was estimated as D = 8.42 × 10–10 m. This derives in large part from the realization that the angular momentum of protons must be to the extent of satisfying the estimation of D by measuring the ionization energy.
The magnetic bipolar of two or more protons does not depend on their positive charge, because the relation D/Dp = 1.28 × 10–4 × c/v–1 (where c = 3 × 108 m/s = speed of light) contains only velocity and dimension. Thus, no matter what Q+ is, D = constant and depends exclusively on the angular velocity of protons. This means that the positive charge is able to interact with other protons or electrons without changing the distance between protons. The above observations show that the space arrangement and the geometry of bioatoms (Figure 3) is constant. Electrons of diameter De are attracted by protons of diameter Dp. These forces give a resultant at the level of planning vertical to the constant flow of the magnetic field or parallel to the planning level. Thus, the forces exercised on the electrons are the external vectorial product of the previous ones, vertical to the planning level. In this way the magnetic field creates a channel vertical to the planning level for each electron. Electrons are now in a symmetrical linear oscillation along this channel due to the influence of the electric Coulomb forces.
The results specify and define the geometric and energy characteristics of the subatomic particles with the use of generally accepted laws of physics, in agreement with established experimental observations.
REFERENCES
- E. Rutherford, “The Scattering of α and β Particles by Matter and the Structure of the Atom,” Philosophical Magazine Series 6, Vol. 21, No. 125, 1911, pp. 669-688. doi:10.1080/14786440508637080
- E. Rutherford, “The Stability of Atoms,” Proceedings of the Physical Society of London, Vol. 33, 1920, pp. 389- 394. doi:10.1088/1478-7814/33/1/337
- H. Torres-Silva, “New Interpretation of the Atomic Spectra of the Hydrogen Atom: Amixed Mechanism of Classical LC Circuits and Quantum Wave-Particle Duality. Ingeniare,” Revista Chilena Ingenieria, Vol. 16, No. 1, 2008, pp. 669-688.
- V. Trimble, “The Origin and Abundances of the Chemical Elements,” Reviews of Modern Physics, Vol. 47, No. 877, 1975, pp. 877-976. doi:10.1103/RevModPhys.47.877
- D. R. Lide, “Atomic, Molecular, and Optical Physics; Ionization Potentials of Atoms and Atomic Ions,” 84th Edition, CRC Handbook of Chemistry and Physics, CRC Press, Boca Raton, 2003.
- G. H. Wannier, “The Threshold Law for Single Ionization of Atoms or Ions by Electrons,” Physical Review, Vol. 190, No. 5, 1953, pp. 817-825. doi:10.1103/PhysRev.90.817
- E. P. Wigner, “On the Behavior of Cross Sections Near Thresholds,” Physical Review, Vol. 73, No. 9, 1948, pp. 1002-1009. doi:10.1103/PhysRev.73.1002
- L. Johansson, Ark. Fys, Vol. 31, 1966, p. 489.
- K. B. S. Eriksson and J. E. Pettersson, “New Measurements in the Spectrum of the Neutral Nitrogen Atom,” Physica Scripta, Vol. 3, No. 5, 1971, p. 211. doi:10.1088/0031-8949/3/5/003
- K. B. S. Eriksson and H. B. S. Isberg, Ark. Fys, Vol. 37, No. 17, 1968, p. 221.
- B. Edlen, “On the Identification of Ar x and Ar xiv in the Solar Corona and the Origin of the Unidentified Coronal Lines,” Solar Physics, Vol. 9, No. 2, 1969, pp. 439-445. doi:10.1007/BF02391668
- K. Liden, Ark. Fys, Vol. 1, 1949, pp. 229-267.
- V. Kaufman and L. Minnhagen, “Accurate Ground-Term Combinations in Ne I,” Journal of the Optical Society of America, Vol. 62, No. 1, 1972, pp. 92-95. doi:10.1364/JOSA.62.000092
- J. F. Baugh, C. E. Burkhardt, J. J. Leventhal and T. Bergeman, “Precision Stark Spectroscopy of Sodium 2P and 2D States,” Physical Review A, Vol. 58, No. 2, 1998, pp. 1585-1588. doi:10.1103/PhysRevA.58.1585
- M. Ciocca, C. E. Burkhardt, J. J. Leventhal, and T. Bergeman, “Precision Stark Spectroscopy of Sodium: Improved Values for the Ionization Limit and Bound States,” Physical Review A, Vol. 45, No. 7, 1992, pp. 4720-4730. doi:10.1103/PhysRevA.45.4720
- V. Kaufman and W. C. Martin, “Wavelengths and Energy Level Classifications of Magnesium Spectra for All Stages of Ionization (Mg I through Mg XII),” Journal of Physical and Chemical Reference Data, Vol. 20, No. 1, 1991, pp. 83-153. doi:10.1063/1.555879
- E. S. Chang, “Solar Emission Lines Revisited: Extended Study of Magnesium,” Physica Scripta, Vol. 35, No. 6, 1987, pp. 792-797. doi:10.1088/0031-8949/35/6/006
- V. Kaufman and W. C. Martin, “Wavelengths and Energy Level Classifications for the Spectra of Aluminum (Ali through Alxiii),” Journal of Physical and Chemical Reference Data, Vol. 20, No. 5, 1991, pp. 775-858. doi:10.1063/1.555895
- E. S. Chang, “Energy Levels of Atomic Aluminum with Hyperfine Structure,” Journal of Physical and Chemical Reference Data, Vol. 19, No. 1, 1990, pp. 119-125. doi:10.1063/1.555870
- W. C. Martin and R. Zalubas, “Energy Levels of Silicon, Si I through Si XIV,” Journal of Physical and Chemical Reference Data, Vol. 12, No. 2, 1983, pp. 323-379. doi:10.1063/1.555685
- N. Svendenius, “The Spectrum and Term Analysis of Neutral Phosphorus, Part I,” Physica Scripta, Vol. 22, No. 3, 1980, pp. 240-287. doi:10.1088/0031-8949/22/3/010
- W. C. Martin, R. Zalubas and A. Musgrove, “Energy Levels of Sulfur, S I Through S XVI,” Journal of Physical and Chemical Reference Data, Vol. 19, No. 4, 1990, pp. 821-881. doi:10.1063/1.555862
- L. J. Radziemski and V. Kaufman, “Wavelengths, Energy Levels, and Analysis of Neutral Atomic Chlorine (Cl I),” Journal of the Optical Society of America, Vol. 59, No. 4, 1969, pp. 424-443. doi:10.1364/JOSA.59.000424
- I. Velchev, W. Hogervorst and W. Ubachs, “Precision VUV spectroscopy of Ar I at 105 nm,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 32, No. 17, 1999, p. L511. doi:10.1088/0953-4075/32/17/105
- J. Sugar and C. Corliss, “Thermodynamic Properties of Key Organic Oxygen Compounds in the Carbon Range C1 to C4. Part 1. Properties of Condensed Phases,” Journal of Physical and Chemical Reference Data, Vol. 14, No. 1, 1985, pp. 1-664. doi:10.1063/1.555747
- C.J. Lorenzen and K. Niemax, “Quantum Defects of the n2P1/2,3/2 Levels in 39K I and 85Rb I,” Physica Scripta, Vol. 27, No. 4, 1983, pp. 300-305. doi:10.1088/0031-8949/27/4/012
- V. Appendix, “Dubbel Taschenbuch fur den Masckinenbau,” Auflage Springer-Verlag, Berlin, 1990.
- W. N. Cottingham and D. A. Greenwood, “Introduction to Nuclear Physics,” 2nd Edition, Cambridge University Press, Cambridge, 2001.
- D. W. Oxtoby, H. P. Gilis and A. Campion, “Principles of Modern Chemistry,” 6th Edition, Thomson, Madrid, 2008.
- A. Landé, Phys. Ge., Vol. 21, No. 2, 1919, pp. 644-653.
- L. Zeit, Physik, Vol. 83, No. 2, 1920, p. 380.
- L. Parson, Smithsonian Institute Publication Miscel, Collections, Vol. 65, No. 11, 1915.
- J. Thomson, “XXIV. On the Structure of the Atom: An Investigation of the Stability and Periods of Oscillation of a Number of Corpuscles Arranged at Equal Intervals around the Circumference of a Circle; with Application of the Results to the Theory of Atomic Structure,” Philosophical Magazine Series 6, Vol. 7, No. 39, 1904, pp. 237- 265. doi:10.1080/14786440409463107
- P. Lenard, “Uber Die Absorption der Kathodenstrahlen Verschiedener Geschwindigkeit,” Annalen der Physik, Vol. 317, No. 12, 1903, pp. 714-744. doi:10.1002/andp.19033171203
- H. Nagaoka, “Kinetics of a System of Particles Illustrating the Line and the Band Spectrum and the Phenomena of Radioactivity,” Philosophical Magazine Series 6, Vol. 7, No. 41, 1904, pp. 445-455. doi:10.1080/14786440409463141
- L. Rayleigh, “On Electrical Vibration and the Constitution of the Atom,” Philosophical Magazine Series 6, Vol. 11, No. 61, 1906, pp. 117-123. doi:10.1080/14786440609463428
- J. H. Jeans, “On the Constitution of the Atom,” Philosophical Magazine Series 6, Vol. 11, 1906, pp. 604-607.
- G. A. Schott, “On the Electron Theory of Matter and Explanation of the Fine Spectrum Lines of Gravitation,” Philosophical Magazine Series 6, Vol. 12, No. 67, 1906, pp. 21-29. doi:10.1080/14786440609463507
- J. Stark, “Prinzipien der Atomdynami: Die Electrishen Quanten,” Verlag Von S. Hirsel, Leipzig, 1910.
- R. Hofstadter, “Structure of Nuclei and Nucleons,” Science, Vol. 136, No. 3521, 1962, pp. 1013-1022. doi:10.1126/science.136.3521.1013

