Open Journal of Physical Chemistry
Vol. 2 No. 1 (2012) , Article ID: 17543 , 6 pages DOI:10.4236/ojpc.2012.21009
The Physics of the Phenomena of Electrical Induced Elements Separation in Solution of Salts in Liquid Polar Dielectric
1National Academy of Sciences of Republic Armenia, Yerevan, Armenia
2Tomsk Polytechnic University, Tomsk, Russia
Email: *shiva@tpu.ru
Received October 28, 2011; revised November 29, 2011; accepted December 28, 2011
Keywords: Electromagnetic Field; Solution; Polar Liquid Dielectric; Solvation; Aqua Complex; Solvated Ion; Hydration Shell; Over-Molecular Cluster; Polarization; Polarized Charge; Directed Drift; Separation; Oscillations; Own Frequencies
ABSTRACT
In the work [1] is shown the possibility of the use the phenomena of the electrical-induced selective drift of cationic aquacomplexes in the water solution of the salts for creating of the new, non-electrode, power-saving technology of the solution enrichment by desired element. The development of the naturally-scientific basis of this technology has showed that inertial properties of formed in the solution over-molecular structural units—clusters depends from that’s dimensions. Dimensions of these clusters are in limits from scores of angstrom to fractions of micron, at the same time liquid mediums are the base of functioning both biological and technological systems. Thus, water solution of salt contains nanoparticles and biological and many technological systems are functioning with the assistance of nanoparticles. For example, the ordinary blood circulatory system or many of chemical processing. The casual or intentional action of aperiodic electric field on systems containing salts solutions produces some positive or negative effects. This work shows new approach for theoretical describing of salts solution in dielectric liquids and contains some data on the realized experiments.
1. Condition of the Problem
At dissolution occurs complex formation therefore is formed supermolecular structure—in water solutions of hydrated aquacomplexes. Aquacomplex may be considered as nanoparticle, formed from central ion and molecules of water.
At action of the external periodic electric field the solvated ions-clusters are drifting [1]. The oriented drift of the polarized solvated ions allows organizing the technological process of element enrichment of water solutions of salts [2]. Experimental researches have shown, that it not the sole appendix of the found out phenomenon (effect). In particular, the solutions of salts of metals in the polar, liquid dielectrics (water, spirits, ketones) show interesting properties at action of the magnetic fields.
As show theoretical and experimental researches, the size of cluster is the quantity determining the majority of physical and technological properties of solutions. Nowadays, two approaches were developed for definition of properties of solutions. The opportunity of use of the plasma concept of a condition of solutions of electrolytes is noted in the works of M. M. Baldanov [3]. The second approach assumes the modeling of processes of solvation on the basis of the incorporated quantum-classical theory of the functional of density [4].
Both in that, and in other case, for the obvious reasons, properties of solutions are defined mainly by energy of multiparty interactions of ions in the dielectric medium. And it uniquely assumes attraction of such individual characteristics, experimental definition of which is impossible (a condition of an electroneutrality), are probable only theoretical estimations, or semiempirical processing of an experimental material on the basis of some plausible, but arbitrary assumptions.
The validity of the assumptions can be certain experimentally, for example, at comparison of observable and theoretical values of any parameter which value directly depends on the solution characteristic of the defined within the limits of this or that approach. Such works have been begun in 30th years of the last century [5].
In the works [3,4] were received the radiuses values of the solvated ions, which compound units of angstroms. Use of such values at a theoretical explanation of the found out phenomenon (effect) of the selective drift of solvated cations under action of an asymmetric electric field [1] leads to estimated values of frequencies of the field (about 100 megahertz) at which it is necessary to expect display of the effect. Nevertheless, the phenomenon takes place at the frequencies which are not exceeding units of kilohertz, and at the certain concentration of salt in water—tens of hertz. Besides there are the experimental data specifying that clusters represent submicron formations [6].
In the work the solution is shown as quasi-neutral system of polarized charges which interacting with external electric field and among themselves. Consideration is spent with the purpose of definition of the geometrical sizes solvated ions—clusters and general characteristics of process of influence on the solution of an external electromagnetic field. Results will allow defining opportunities of various appendices of the found out phenomenon (effect).
2. The Self-Consistent Field in the Solution of Salt in the Liquid Polar Dielectric
Let’ consider, that each cation (anion) causes the polarization of surrounded solvent (water): the “atmosphere” is forming around each cation (anion) with abundance of polarized molecules of the water. This “atmosphere” is shielding cation’s (anion’s) field. The generalized electronic shell of each polarized molecules of water is deformed concerning unperturbed configuration, when full spin of the molecule is a zero. The perturbation is caused by the action of the cation’s (anion’s) electric field. The deformation of the shell is cause that the part of nucleus’ charge or electrons in the water’s molecule will be uncompensated. This uncompensated part of a charge represents a polarizing charge of a molecule of water in a non-uniform electric field of the charged particle—cation (anion). According to representation about the self-coordinated field [7] there is such distribution of an electric field in system of the cooperating charged particles which creates the distribution of particles exciting a field. Salt solution is possible to consider as system of cooperating cations, anions, it is positive and negatively polarized molecules of water. For a finding of the self-coordinated field we shall use Poisson equation:
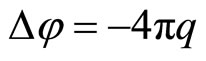 (1)
(1)
and Boltzman distribution:
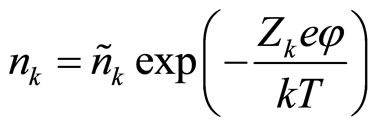 (2)
(2)
where nk—concentration of particles with charging number Zk in a point with potential j. For electrons, for example, Z = –1. But in a solution are not present free electrons. For cations Z = m, and for anions Z = –m, where mvalency of metal which salt is dissolved. nk in distribution (2) is a concentration of particles with charging number Zk in a point with the zero potential, equal to average concentration of these particles on all volume of a solution.
Further an index “i” we shall designate cations, an index “a” – anions, “p+”—polarized and being around of anions molecules of water, “p–”—molecules of water around cations.
Average concentration nk satisfies to a condition of quasi-neutrality:
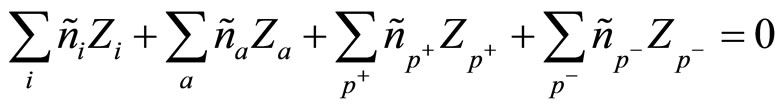 (3)
(3)
which show the fact, that the solution as a whole (from outside) is neutral.
Also following conditions take place:
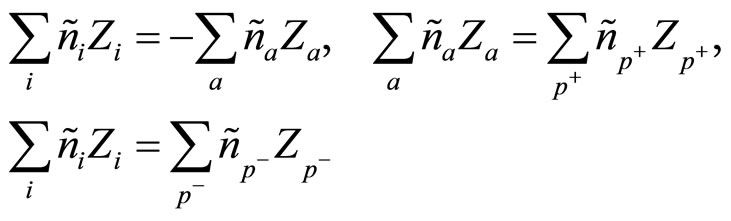 (4)
(4)
In which it is considered, that charging numbers of cation and anion are equal on absolute value, but opposite, and charging numbers of the polarized molecules of water are determined by around of what they associated: around anions , and around cations
, and around cations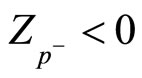 .
.
Thus,
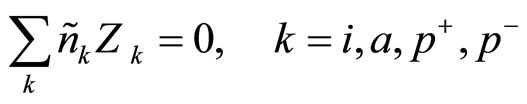 (5)
(5)
Also following connections take place:
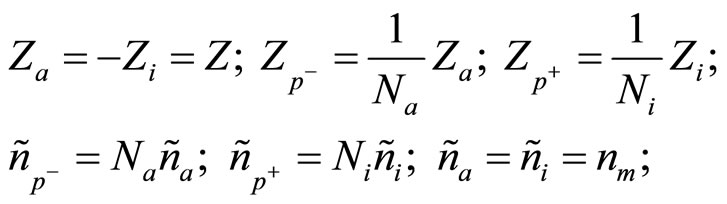 (6)
(6)
where Na—number of molecules of water, associated around of one anion; Ni—number of molecules of water, associated around of one cation; Z—valency of metal, which salt is dissolved; nm—concentration of molecules of salt in a solution, if to consider they are not dissociated.
Volume charge thus,
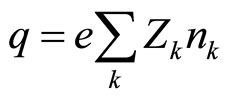 (7)
(7)
where e—the module of a charge of electron (in system SI 1.6∙10–19 C). The correlation (7) is very similar to expression (5) with that essential difference, which in it there is a value of concentration of particles in that point in which the potential of the self-coordinated field is determined.
Equation of Poisson will copy in the form of:
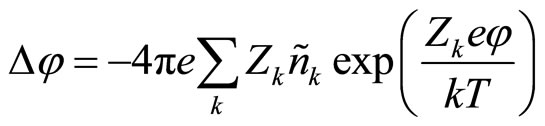 (8)
(8)
Using series expansion and considering connections (4) and (6), it is possible to receive function:
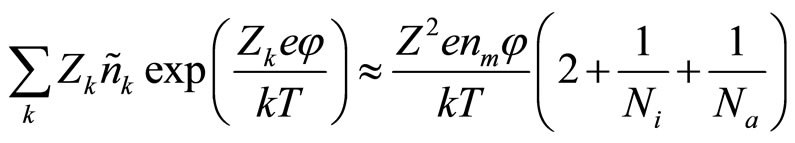 (9)
(9)
Even if takes place no more, than secondary hydration, in hydrate shell it will be concentrated more than 10 molecules of water. Therefore it is possible to considerthat  and
and . In view of this, equation of Poisson will become:
. In view of this, equation of Poisson will become:
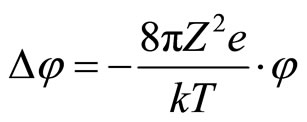 . (10)
. (10)
The decision (10) for spherical symmetric distribution of potential (cation or anion) looks like:
 , (11)
, (11)
where constant of insulation is:
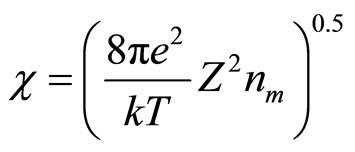 (12)
(12)
The inverse value 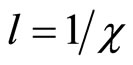 refers to as length of insulation and it is possible to consider, that its value defines radius of solvation sphere within the limits of which the polarized molecules of water are built. They also insulate a field of cation (anion). Thus, value of cluster radius (solvated cation or anion) can be estimated, using:
refers to as length of insulation and it is possible to consider, that its value defines radius of solvation sphere within the limits of which the polarized molecules of water are built. They also insulate a field of cation (anion). Thus, value of cluster radius (solvated cation or anion) can be estimated, using:
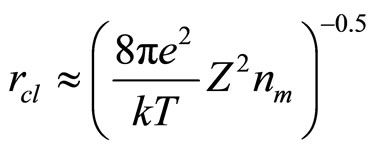 (13)
(13)
3. The Characteristic Values of Frequencies of Excitation of Effect of Oriented Drift of the Solvated Ions
The own frequency of solvated ion (cluster) can be expressed of following equation: 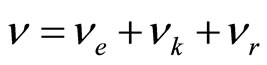 , where items correspond of frequencies of excitation of electron shells (e), oscillation an ion and solvated groups (k) and rotations solvated groups concerning an ion (r). It is supposed, that excitation of electronic shells or oscillation of ion and solvated groups can be initiated only after deformation solvated shell (screen), which inhibits influence of an electric field. Deformations (rotation solvated groups concerning an ion) correspond to item
, where items correspond of frequencies of excitation of electron shells (e), oscillation an ion and solvated groups (k) and rotations solvated groups concerning an ion (r). It is supposed, that excitation of electronic shells or oscillation of ion and solvated groups can be initiated only after deformation solvated shell (screen), which inhibits influence of an electric field. Deformations (rotation solvated groups concerning an ion) correspond to item 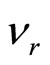 .
.
Frequencies of transition of oscillatory motions in rotary are defined by equation:
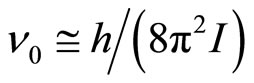 (14)
(14)
where h—Planck’s constant, I—the moment of inertia of system of the connected particles. The given equation is valid if cluster it is possible to consider as linear system of two rigidly connected particles (an ion and solvated shell), and oscillatory movement of any of particles causes rotation of cluster as the whole. These frequencies in conditions of the achievement of relative mobility of clusters, which is required for activation of process of the selective drift under influence of field, is possible to considered as the minimum frequencies of own free movements clusters. Broader range of frequencies of own motions of clusters, which is connected with free rotaryonward motions, can be presented in the form of set of the frequencies of the allowed quantum levels of free rotation by analogy to a spherical top (all of its three principal of the moment of inertia are equal):
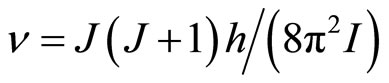 (15)
(15)
and frequencies of onward moving:
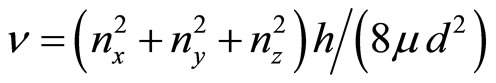 (16)
(16)
where J—quantum number, nx,y,z—the projections of the vector of the rotation to coordinate axes, d—the size of cluster, μ—the brought weight of cluster. The frequency of onward moving is meant frequency of rotation of all clusters (an ion together with the solvated shell) as the whole when sets of all three main directions of the fluctuations will be transformed in each other If in Formulae (15)-(16) the form of cluster take as spherical—“zero” approach, it is possible to consider, that J = 1,  . The number of the molecules of water (the solvated groups) in the cluster, having radius rcl, is g, d = 2rcl,
. The number of the molecules of water (the solvated groups) in the cluster, having radius rcl, is g, d = 2rcl, 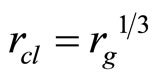 ,
, 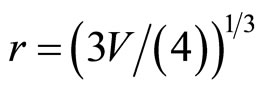 , where r, V—radius and volume of the solvated groups, respectively. Thus
, where r, V—radius and volume of the solvated groups, respectively. Thus  , where Kr—the factor equal to the relation of the moment of inertia, corresponding rotation solvated shell around of an ion, to average of value of the projection of the oscillatory moment on the axis of rotation. This factor characterizes intensity of the Carioles interactions (the analogy to Carioles forces in the classical mechanics). It have value 0.4 for the rotation the solvated shell around cation (anion) and 1.4—for the rotation around axis, passing regarding to surface cluster. As the weight of the solvated shell considerably surpasses weight of the ion, positions of the centre of gravity (the center of inertia) and the ion practically coincide. The values of the frequencies received in the Formulae (14)-(16) for J = 1 (the minimal values), correspond to a case when only one aquacomplex is formed, and allow to estimate only values of the frequencies which should be expected in the experiments.
, where Kr—the factor equal to the relation of the moment of inertia, corresponding rotation solvated shell around of an ion, to average of value of the projection of the oscillatory moment on the axis of rotation. This factor characterizes intensity of the Carioles interactions (the analogy to Carioles forces in the classical mechanics). It have value 0.4 for the rotation the solvated shell around cation (anion) and 1.4—for the rotation around axis, passing regarding to surface cluster. As the weight of the solvated shell considerably surpasses weight of the ion, positions of the centre of gravity (the center of inertia) and the ion practically coincide. The values of the frequencies received in the Formulae (14)-(16) for J = 1 (the minimal values), correspond to a case when only one aquacomplex is formed, and allow to estimate only values of the frequencies which should be expected in the experiments.
As follows from the ratio (13), the value of dimension of the cluster is inversely to a square root from value of concentration of salt in water. Values of the frequencies are inversely to the value of the moment of inertia of the cluster. The moment of inertia is proportional to the equivalent mass of the cluster, that is the quantity of molecules of water in the solvated shell 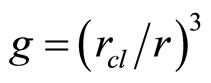 , and the square of radius of cluster rcl2. It turns out, that the moment of inertia I ~ rcl 5 and values of the frequencies of excitation of various components of motions
, and the square of radius of cluster rcl2. It turns out, that the moment of inertia I ~ rcl 5 and values of the frequencies of excitation of various components of motions 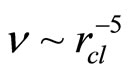 . Thus, values of the frequencies
. Thus, values of the frequencies  .
.
At present time there are several used approaches but only two forms that are checked in experiments. One of them was investigated for concentration of the salts in water solution, providing performing the condition 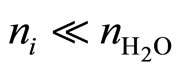 , where
, where 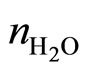 —an amount of the molecules of water in unit of the volume,
—an amount of the molecules of water in unit of the volume,  —for amount ion ditto, it is possible to expect that: potential becomes too small on distances, smaller distances between most close located ions [1]. Values of frequencies, corresponding to different components of the rotary-onward motion of cationic aquacomplexes, and values of the frequencies, corresponding to the turning of the oscillatory motion in rotary, are in limits from several hundreds Hertz to several kiloHertz. If the solution is considered as quasi-neutral system of polarized charges which interacting with external electric field and among them, frequencies of oscillations are much less (no more than 100 Hertz).
—for amount ion ditto, it is possible to expect that: potential becomes too small on distances, smaller distances between most close located ions [1]. Values of frequencies, corresponding to different components of the rotary-onward motion of cationic aquacomplexes, and values of the frequencies, corresponding to the turning of the oscillatory motion in rotary, are in limits from several hundreds Hertz to several kiloHertz. If the solution is considered as quasi-neutral system of polarized charges which interacting with external electric field and among them, frequencies of oscillations are much less (no more than 100 Hertz).
4. The Fluctuations of the Polarized Charge in the Solution
In external electric field polarized due to deformation of the aquation shell of aquacomplexes are displaced. As a result there is a division of the aquacomplexes, displaced to a greater or lesser extent. Polarized charges of the divided aquacomplexes differ, at least, on absolute value. Thus, there is a division of charges and electrostatic forces in volume of a solution. Electrostatic forces should lead to excitation of own electrostatic fluctuations in volume on the average neutral (in an enough great volumes or for enough greater time intervals) a solution.
Let as a result of division of the polarized aquacomplexes in a solution there is a polarized charge q. Thus
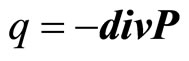 (17)
(17)
where 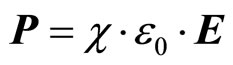 —a vector of polarization;
—a vector of polarization;  —a dielectric susceptibility of a solution;
—a dielectric susceptibility of a solution;  —an electric constant of vacuum; E—a vector of intensity of the electric field acting on a solution. We shall remind that it is a question of solutions of salts of metals in polar dielectric liquids. Thus
—an electric constant of vacuum; E—a vector of intensity of the electric field acting on a solution. We shall remind that it is a question of solutions of salts of metals in polar dielectric liquids. Thus
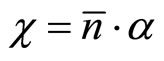 (18)
(18)
where  —factor of polarizability of the solvated ion— cluster;
—factor of polarizability of the solvated ion— cluster; 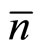 —average number of clusters in unit of volume of a solution, and
—average number of clusters in unit of volume of a solution, and 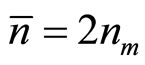 , where nm—number of dissociating molecules of salt in unit of volume of a solution.
, where nm—number of dissociating molecules of salt in unit of volume of a solution.
The polarized charge of one cluster 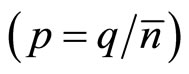 will be defined, thus, by expression:
will be defined, thus, by expression:
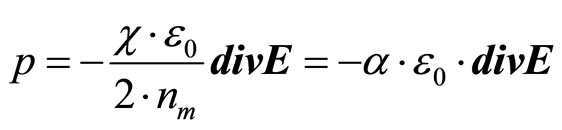 (19)
(19)
The According to the law of preservation of a charge
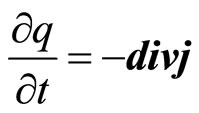 (20)
(20)
where j—density of a current. Thus the current is carried by the polarized aquacomplexes. Then
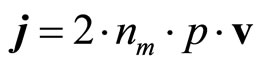 (21)
(21)
where v—speed of the aquacomplexes, carrying a current. The equation of movement polarized aquacomplex, having weight m, will enter the name in the form of
 (22)
(22)
Differentiating the Equations (20) and (21) and substituting (21) in (20), we shall receive
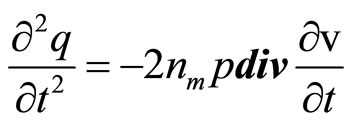 (23)
(23)
Substituting in (23) expression for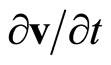 , received of (22), and considering, that
, received of (22), and considering, that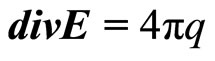 , we shall receive
, we shall receive
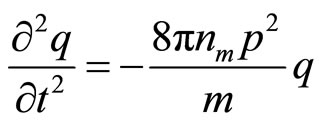 (24)
(24)
The received equation describes simple harmonious fluctuation with circular frequency
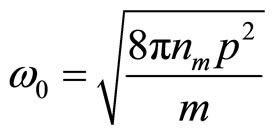 (25)
(25)
If the solution is placed between two flat electrodes, the distance between which is not great, consideration of process can be spent in one-dimensional geometry. We shall designate through  absolute value of intensity of the electric field acting on a solution. Then
absolute value of intensity of the electric field acting on a solution. Then
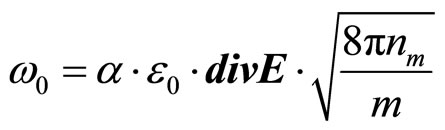 (26)
(26)
or
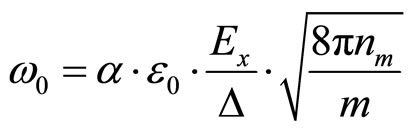 (27)
(27)
where ∆—thickness of a layer of a solution between the potential and earthed flat electrodes.
Thus, the density of a volumetric polarized charge in a solution will change with circular frequency 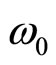
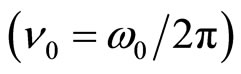 after action on a solution of an external electric field. Thus frequency of fluctuations is defined not by amplitude of intensity of this field, and divergence of intensity of a field in volume of a solution.
after action on a solution of an external electric field. Thus frequency of fluctuations is defined not by amplitude of intensity of this field, and divergence of intensity of a field in volume of a solution.
5. Electromagnetic Wave Action on the Solution
As well as in plasma, any separation of charges in a solution of salt in liquid polar dielectric leads to fluctuations of density of a charge. On the average for many periods of fluctuations the solution behaves as quasi-neutral medium. Separation of polarizing charges is possible only on temporary intervals, smaller in comparison with temporary scale of separation of charges 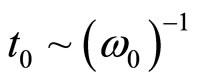 . For spatial scale of separation of the charges d it is possible to accept distance which solvated the ion at the thermal movement migrate in time t0, that is
. For spatial scale of separation of the charges d it is possible to accept distance which solvated the ion at the thermal movement migrate in time t0, that is 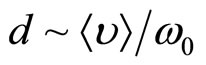 , where
, where 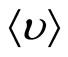 —the average speed of thermal movement of solvated ions (clusters), having weight m. In spatial scales, greater in comparison with d, it is observed quasi-neutral the solution.
—the average speed of thermal movement of solvated ions (clusters), having weight m. In spatial scales, greater in comparison with d, it is observed quasi-neutral the solution.
By definition the dielectric constant of the continuous environment e is the relation of intensity of external electric field Е to intensity of the weakened field inside of this medium  (dielectric). Thus e always is more than 1.
(dielectric). Thus e always is more than 1.
In a solution 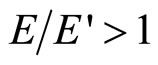 . Hence for a solution e < 1. Thus the smaller frequency of an external electric field w,
. Hence for a solution e < 1. Thus the smaller frequency of an external electric field w,  , the more “range” of fluctuations polarized solvated ions, that is amplitude of their displacement. It turns out, that with diminution of w the dielectric constant of a solution e decreases also.
, the more “range” of fluctuations polarized solvated ions, that is amplitude of their displacement. It turns out, that with diminution of w the dielectric constant of a solution e decreases also.
Also behave also free electrons in plasma that is used in techniques of sounding of plasma by radiowaves. In case of plasma is critical value of frequency wk of radiowaves, at which dielectric constant of plasma e = 0. Value of this frequency coincides with value the Longmuir frequencies of plasma.
In our case the analogue of Longmuir frequencies is frequency of fluctuations of the polarized charge in volume of a solution w0.
The dielectric constant of plasma is defined by the ratio:
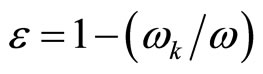 (28)
(28)
where w—frequency of an external radio emission. If this frequency w < wk, then e < 0.
In Maxwell’s works it is established, that factor of refraction of an electromagnetic wave in substance  . At e < 0 electromagnetic waves cannot extend in substance and should be reflected completely from it. Therefore in relation to waves with frequency w < wk plasma is an ideal reflector. By analogy it is possible to assume, that a solution salt in liquid, polar dielectric will be a reflector for waves with frequency
. At e < 0 electromagnetic waves cannot extend in substance and should be reflected completely from it. Therefore in relation to waves with frequency w < wk plasma is an ideal reflector. By analogy it is possible to assume, that a solution salt in liquid, polar dielectric will be a reflector for waves with frequency
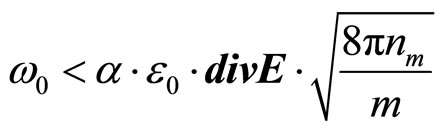 (29)
(29)
where Е—intensity of an electric field in a wave.
6. Conclusions
The solvation process of ions in solutions of salts in liquid, polar dielectrics provides an opportunity of development of essentially new technologies and techniques. The conditions providing use of process mass transfer for the decision of various applied problems, first of all are defined by the sizes of solvated ions (clusters).
In particular, action of periodic electric fields with various combinations of frequency, intensity and the attitude of amplitudes of intensity in half-cycles on solutions of salts in polar dielectrics causes excitation of rotary-forward motion solvated ions (clusters) and, hence, mass transfer.
On the Figure 1 is shown the scheme of experimental cell which was constructed for separation of solvated ions of cerium and lanthanum.
At submission on the input of the separating element on the basis of a technological cell of the base mixture of two component (a water solution of the mix of salts Ce(NO3)3 and Y(NO3)3 with concentration 3.5 and 3 g/l, accordingly) the separation factor in an element without circulation of the solution after 4 hours of influence of the field with intensity Е+ = 14.3 V/cm, factor of asymmetry A–/A+ = 0,66, with frequency 1.6 kHz have made: in the selection 1.00499; in the dump 1.00179; full 1.00679. In a solution there was an enrichment on the cations Ce3+.
Checking of the condition of water in the solutions of sugars (a-methyl-D-glucopyranoside, a-methyl-D-mannopyranoside, a-methyl-D-glucopyranoside, Lactose and
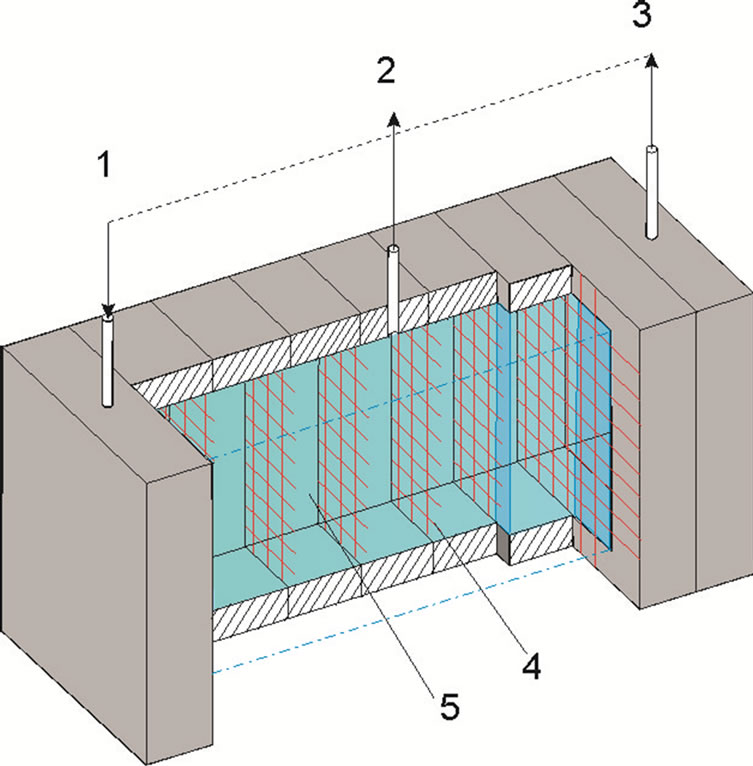
Figure 1. Technological cell: 1—nipple for the solution inlet; 2—nipple for the solution selection; 3—nipple for the solution selection and circulation; 4—insulated potential hightransparent nets; 5—solution.
saccharine) by means Spectrophotometer Perkin-Elmer Model 180 have showed, that a marked difference occurs between spectrums of light absorption by solution before and after asymmetrical electric field action. The received facts confirm that action of field on the solution causes either changes of certain conditions of water in the solution or changes of biological active compounds concentrations in the gap between potential and neutral electrodes.
Action of an electromagnetic wave on a solution salt in liquid, polar dielectric causes division of charges and leads to fluctuations of density of a charge. At the certain combinations of parameters of an electromagnetic wave and a solution it is possible to expect partial or its full reflection from the medium formed by a solution that allows considering the problem opportunities of use of electromagnetic waves for definition of parameters of solutions.
REFERENCES
- M. A. Kazarjan, I. V. Lomov and I. V. Shamanin, “Тhе Physical Models and Applications of the Solvation Process in Salts Solution in Polar Dielectric,” International Scientific Journal for Alternative Energy and Ecology, Vol. 11, No. 55, 2007, pp. 145-154.
- A. L. Gusev, M. A. Kazarjan, Yu. A. Trutnev, I. V. Shamanin and I. V. Lomov, “The Non-Electrode Technology of the Water Solution Enrichment by Desired Element in the Complex Conversion of Nucleus Raw Material,” International Scientific Journal for Alternative Energy and Ecology, Vol. 3, No. 47, 2007, pp. 49-52.
- M. M. Baldanov, B. B. Tanganov and M. V. Mohoseev, “Conduction of Water Solution of the Weak Acids,” Doklady Akademii Nauk SSSR, Vol. 299, No. 4, 1988, pp. 899-904.
- M. V. Fedorov and A. A. Kornishev, “Unravelling Solvent Response to Neutral Charged Solutes,” Molecular Physics, Vol. 105, No. 1, 2007, pp. 1-7. doi:10.1080/00268970601110316
- A. N. Terenin, “Spectrums of the Absorption of Electrolytic Solutions,” Uspekhi Phyzicheskikh Nauk, Vol. 17, No. 1, 1937, pp. 2-54.
- Yu. K. Stishkov and A. V. Steblianko, “The Breach of Homogeneity of the Weakly Conducting Liquids in Strong Electric Fields,” Zhurnal Tekhnicheskoi Fiziki, Vol. 67, No. 10, 1997, pp.105-111.
- D. A. Frank-Kamenetskiy, “Lekcii po Phyzike Plazmi,” Atomizdat, Moskow, 1968.
NOTES
*Corresponding author.

