Received 10 April 2015; accepted 27 June 2015; published 30 June 2015

ABSTRACT

Given the scientific progresses as well as the invention of new methods in exploration, it is necessary to conduct some re-investigations in several exploration zones. So, in the present research, geochemical data on Tanurjeh exploration zone, (located in Northern Neishaboor, Khorasane Razavi province) is studied by using some modern statistical methods. Fractal methods are appropriated to study and separate the grades societies in deposits. In this article, litho-geochemical analysis results (ICP) are processed by concentration area fractal method (CA). The distribution diagrams related to the statistical populations are drawn, and anomaly populations of Copper, Gold and Molybdenum are determined besides previous studies (petrography and alteration), the results of statistic methods (CA) and aid presence of the porphyry system in depth.

Keywords:

Concentration Fractal Method, Litho-Geochemical Data, Tanurjeh Area

1. Introduction

The study area is located in Khorasan Razavi province, in south of Neyshabour city and Tanurjeh village (longitude 58˚35'23"E to 58˚39'13"E east and latitude 35˚23'75"N to 35˚21'38"N north).

From tectonically point of view, this area is located in Khaaf-Doruneh belt at the northern part of the Daruneh fault. Tectonic conditions of this belt and Tertiary magmatic activities form different mineralization in the area in comparison with other places (Figure 1).

2. Lithology

According to the field and microscopic studies, lithology of the area was distinguished as follows (Figure 2) [1] :

1) Acidic volcanic rocks such as Rhyolite to Rhyodacitic tuffs and lavas, which has main dispersion especially in western part of the study area.

2) Eocene sub-volcanic rocks in small stocks and dykes form. These rocks were introduced as two major groups: Monzonite porphyry and Diorite porphyry. By thin section studies, the following variety was distinguished:

Quartz-alkali-monzonite, Quartz-monzonite-porphyry, Biotite-quartz-monzonite porphyry, Hornblende-bio- tite-quartz-monzonite porphyry, Diorite to monzo-diorite porphyry, Hornblende monzo-diorite porphyry.

According to the field studies, lithology and alteration types and its pattern, a small porphyry system was recognized in depth [1] . Applying, using fractal method (CA) and distribution pattern of copper, gold and molybdenum have been also confirmed the aim.

3. Fractal Concentration Area Method

Cheng et al. (1994) [2] proposed the fractal concentration-area (C-A) model for separating geochemical anomalies from background in order to characterize the distribution of major, minor and trace element concentrations in relation to the Mitchell-Sulphurets porphyry system in British Columbia (Canada). This model has the general form:

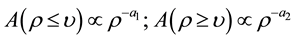
where A(ρ ≤ υ) and A(ρ ≥ υ) denote areas (A) with concentration values ρ that are, respectively, smaller and greater than contour value ρ defining that areas (υ represents the threshold), which define those areas and a₁ and a₂ are characteristic exponents for both criteria. In log-log plots of concentration contours versus areas, certain concentration contours representing breakpoints in the plots are considered threshold values separating geochemical populations in the data. Zou et al. (2009) [3] applied the fractal C-A method to characterize the vertical distribution of element concentrations in the Qulong copper deposit, Tibet, western China. Fractal models have

been used to identify the vertical distribution properties of Cu concentration values in mineralized and non-mi- neralized zones. Cheng (2008) [4] described hydrothermal processes in the Earth’s crust associated with ore deposits, such as porphyry ore deposits, which are characterized by high metal concentrations of metals with having fractal or multifractal properties.

Plotting the log-log graph of changes versus grade, it will be possible to calculate the dimension of each population by the slope of the corresponding fitted line. Breakpoints (change in the slope of the fitted line) in this diagram represent statistical population changes, so that it is possible to separate the possible and definite anomalies for an element and even, in some cases, major and minor mineralization. If the fractal curve represents only two statistical populations, that is to say there is only one breakpoint, it will be said that the element has one-fractal behavior in the study area. But this case happens rarely, and there is always more than two separate statistical populations. This is a fact which was named multi-fractalcharacteristic of data by mandelbort (1983) [5] . Being multi-fractal means having more than two breakpoints on the grade versus cumulative area log-log plot. So, in terms of geology and geochemistry, more than two separate statistical populations will be seen of the region [6] .

Changes of statistical populations in this method is a function of changes in geological conditions such as mineralization, alteration, mineralogy, lithology, sedimentation, tectonic and metamorphism [2] [7] and even factors such surface weathering and surface distribution of elements in the region [6] .

This fact is well observed in the multi-fractal data behavior. In addition to separating background from anomaly, another important help is separating anomalies of different degrees from each other, that is to say it will be possible to separate possible, potential, and certain anomalies, in addition to the cutoff grades [8] .

Considering the aforementioned potentials and parameters, today, CA fractal method is one of the most widely used tools in surface exploration for separating geochemical and geophysical anomalies. After the method was introduced, it became the basis for a lot of newer used-in-exploration fractal methods. Overall, the method has many advantages compared to those methods that are similarly used in classic statistic. In this method, all the data is used, and no special adjustment related to classic statistic methods such as omitting out of raw or normalization is made to the existing data. In methods which are based upon classic statistic, data are considered as being separated from each other, and no geologic conditions are applied while distributing the data. Also, use of mathematic formulae in classic statistic methods depends on whether or not the data is normalized [9] .

4. Evaluation of the Geochemical Data

Among the geochemical data related to this area [1] , copper, molybdenum, and gold, which are the main elements in porphyry deposits, have been evaluated and studied.

The results of these evaluations are as follows:

5. Determination of Copper Anomalies

Four statistical populations were specified for copper by using the CA fractal method (Figure 3). The values less than 14.12 ppm, were considered for first population which are equal to the background cutoff in this area. For the second population, the copper grade was deemed to range from 14.12 to 100 ppm which are equal to the first anomaly population. The copper grade in the third statistical population has the values ranging from 100 to 501.18 ppm. These values are equal to the second anomaly population. Finally, the fourth population included the values larger than 501.18 ppm which are equal to the main anomaly of copper within the area.

After specifying the statistical populations, the anomaly map of the area was plotted. It was determined that Cu is mainly concentrated in the western part of the area where concludes monzo-diorite to diorite intrusive bodies and Eocene pyroclastic rocks (Figure 4).

6. Determination of Gold Anomalies

Similar to Cu, four statistical populations were also specified for Au (Figure 5). The values less than 47.76 ppb, were considered for the first population which are equal to the background cutoff in this area. For the second population, it was deemed to range from 47.76 to 125.89 ppb which are equal to the first anomaly population. Au grade in the third statistical population has the values ranging from 125.89 to 398.1 ppb. These values are equal to the second anomaly population. Finally, the fourth population included the values larger than 398.1 ppb which are equal to the main anomaly.

After plotting the anomaly map, some concentrations of Au were distinguished in north, northwestern, western, and southern part of the area (Figure 6). It is remarkable that the presence of these anomalies is along with the intrusive and sub-volcanic bodies.

7. Determination of Molybdenum Anomalies

Four statistical populations were specified for molybdenum (Mo) by using the CA fractal method. For the first population, Mo grade was considered the values less than 5.75 ppm. These values are equal to the background cutoff. For the second population, Mo grade was deemed to range from 5.75 to 10.9 ppm which are equal to the first anomaly population. Mo grade in the third statistical population has the values ranging from 10.9 to 30.1 ppm which is equal to the second anomaly population. Finally, the fourth population included the values larger than 30.1 ppm which are equal to the main anomaly of Mo (Figure 7).

After plotting the anomaly map of Mo, some concentrations were distinguished in southern, western, and northwestern part of the area (Figure 8). As shown in this figure, distribution of molybdenum is different from those of copper and gold. So, it can be concluded that the accumulation of this element is inconsistent with that of copper indicating the presence of a copper-gold porphyry system and not a copper-molybdenum one in the study area.

8. Conclusion

Geochemical studies on copper, molybdenum and gold by using the concentration-area fractal method in Tanurjeh show the main accumulation of copper in the western part, which is consistent with the second priority of gold. In terms of lithology, the area contains sub-volcanic intrusive bodies composed of Monzonite and Diorite

porphyry, which have intruded in Eocene tuffs. The alteration variety (propylitic, phyllic and argillic) and its pattern in the first priority strengthen the hypothesis of presence in the center of porphyry system in depth. Also, the second and third priorities of gold may be due to the hydrothermal activities happened in the mentioned area. In the other hand, in the southern part where concentration of molybdenum is increased, we are faced with reduction of copper and gold concentration. These evidences lead us to conclude presence of a dioritic porphyry system in depth.

References

NOTES

^*Corresponding author.