Open Journal of Geology
Vol. 2 No. 3 (2012) , Article ID: 21391 , 5 pages DOI:10.4236/ojg.2012.23020
Macroscopic Young’s Elastic Modulus Model of Particle Packing Rock Layers
1State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum, Beijing, China
2the College of Geosciences and Resources, China University of Geosciences, Beijing, China
3Institute of Disaster Prevention, Sanhe, China
Email: *gcywww@126.com
Received May 21, 2012; revised June 15, 2012; accepted June 23, 2012
Keywords: particle contact; Macroscopic Young’s Modulus; arrangements of particle
ABSTRACT
Based on the Hertzian granular contact mechanics model, the paper built up a Macroscopic Young’s Elastic Modulus of particle/granular packing rock layers, and built up a ties to connecting Young’s Elastic Modulus of sand particle in Meso and the Macroscopic Young’s Modulus of granular packing rock layers. The Macroscopic Young’s Modulus of granular packing rock layers is far less than the Young’s Modulus of sand particle. The Macroscopic Young’s Modulus of granular packing rock layers is proportioned to the powers of 1/3 of the vertical contact force of sand particles. The Macroscopic Young’s Modulus is inversely proportional to particle diameter. The paper calculated the vertical contact force of five types aligning mode of the particles. When equal stress, the increased of the coordination number lead to the decrease of the contact force fn, this lead to the coordination number is an inverse proportion to Macroscopic Young’s Modulus. But the larger coordination number change only means very little Macroscopic Young’s Modulus change.
1. Introduction
Young’s Modulus of rocks or soil is the important parameters in calculating seismic velocity, liquefaction of sand-soil, seismic exploration and hydrocarbon prediction, earthquake engineering, tunnel excavating, deformation of sand body, dynamic diagenesis of sandstone. Scholars always study the macroscopic structure of porous media used the relation of wave velocity and density of material experientially. But there was a positive correlation between wave velocity and Young’s Modulus theoretically and this logical accords with the principle of wave propagation. The difference between experiential methods and theoretical methods make the engineering application method and entirely pure research model each go its own way. Young’s Modulus obtained by experiment mostly. But few studies focused on Young’s Modulus of granular mixtures or granular packing rock layers. Liu Xu (2002) [1] used multi-phase medium micromechanical model to educe out some macroscopic elastic parameter. But Liu’s method was based on most hypothesis on factor of porosity [2]. Zhong Xiao-xiong (1992) [3] set up the relationship between fabric tensor and contact density distribution functions, and the relationship between fabric tensor and stress tensor are analyzed. Those model on stress tensor and arrangements of particle is too fussy to used on geologic and macroscopic mechanics of rocks and soils.
The Macroscopic Young’s Modulus of dry particle or granular packing rock layers is an important method to distinguish elastic deformation and plastic deformation of sedimentary rock layer. “From a grain sand can we find a world?”. The paper effort to set up a ties model between the macroscopic elastic parameter of granular packing rock layers and the elastic parameter of those sand particles. And effort to make out a series of simple theoretical logics and catch hold of those dominant factors of those logics. Maybe this can help those investigators and engineers to qualitatively and semi-quantitatively grasp the macroscopic elastic parameter of unconsolidated sandstone.
2. Model of Elastic Contact
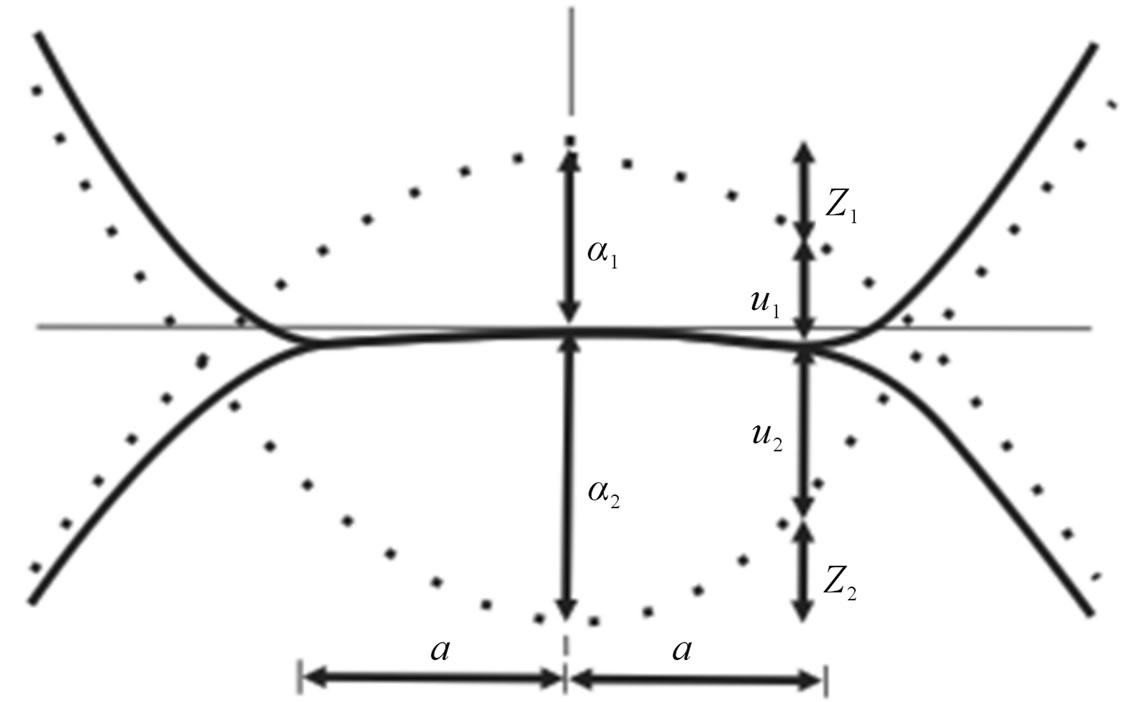
Based on the mechanics of spherical particles contact, classical Hertzian contact theory (Johnson, 1985 [4]; Oda, 1999 [5]; Sun Qi-cheng, 2009) [6] consider that the contact points transformed into interface after the elastic deformation. As Figure 1(a) shows.
The Hertzian contact theory as formula 1 to 7 shows.
Among Figure 1, a is the round radius of the contact interface and its distribution as Figure 1(b) shows. The 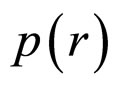 leads to normal displacements u over the contact area. The distribution of normal deformation amounts u of different spherical particles after the normal contact force fn. So, the deformation amounts of v of different points in a contact interface as formula 3 shows. The
leads to normal displacements u over the contact area. The distribution of normal deformation amounts u of different spherical particles after the normal contact force fn. So, the deformation amounts of v of different points in a contact interface as formula 3 shows. The  is the relative approach of the centroids of the two sphere in contact.
is the relative approach of the centroids of the two sphere in contact.
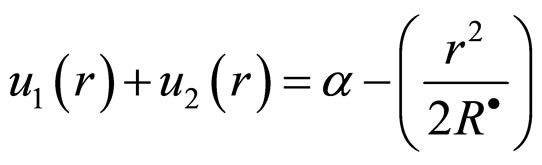 (1)
(1)
Among them,
 (2)
(2)
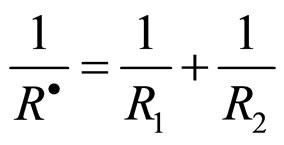 (3)
(3)
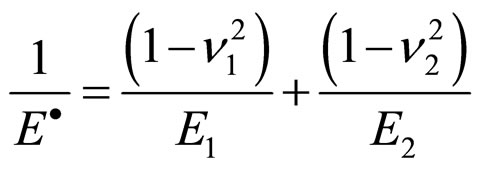 (4)
(4)
 (a)
(a)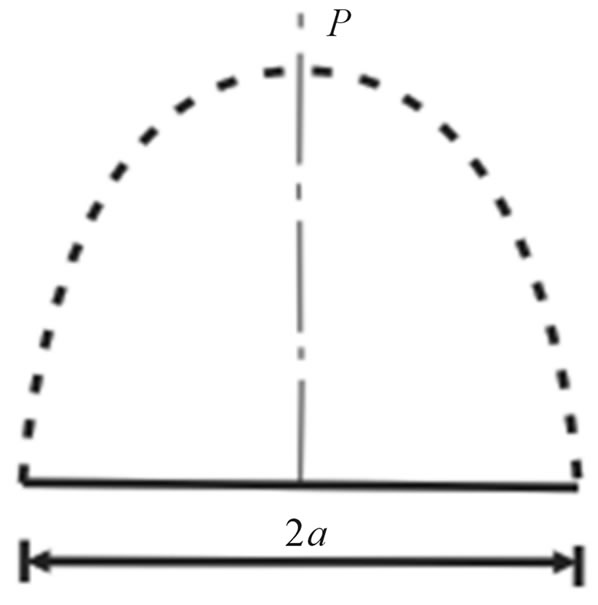 (b)
(b)
Figure 1. Hertzian contact model [5]. (a) Geometry of hertzian contact between two dissimilar, unequal sized elatstic spheres subjected to an applied normal force; (b) Normal contact force distribution of Hertzian contact.
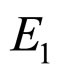 and
and  is the material’s Young’s Modulus of spherical particles.
is the material’s Young’s Modulus of spherical particles. 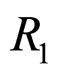 and
and 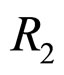 is the radius of particles 1 and particles 2,
is the radius of particles 1 and particles 2,  and
and 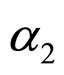 is the Max normal deformation amount of particles 1 and 2. So, the total normal force is defined as formula 5.
is the Max normal deformation amount of particles 1 and 2. So, the total normal force is defined as formula 5.
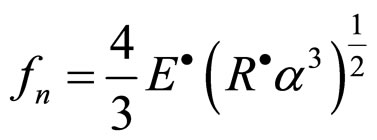 (5)
(5)
The inverse ratios of Normal Contact Stiffness 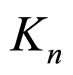 can express the normal direction deformation amount between two particles center by unit normal direction force.
can express the normal direction deformation amount between two particles center by unit normal direction force.
 (6)
(6)
Sun Qi-cheng [6] thought that if the normal deformation amount 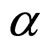 is little, according to as formula 9, the force may be calculated by Hooke’s Law. And some studies looks the
is little, according to as formula 9, the force may be calculated by Hooke’s Law. And some studies looks the 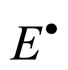 in formula 6 as the Shearing Young’s Modulus also mean a great errors.
in formula 6 as the Shearing Young’s Modulus also mean a great errors.
3. Macroscopic Young’s Modulus
The Macroscopic Young’s Modulus is the Young’s Modulus of particle packing rock layers. It is smaller than the material’s Young’s Modulus of spherical particles. Because of the different of material’s and rock layer’s, the wave velocity of various depth or petrofabric of rock layers is different. The percentage of sedimentary rock of the rock cover the earth surface was 75% and formed in sand particle packing layer. The compaction and diagenesis in particle packing layer is also the process of pore evolution and change of Macroscopic Young’s Modulus. Liu Yu (2010) [7] and Xia Tang-dai (2011) [2] put forward the concept of “effective shear modulus” and expression the relation between the material’s Young’s Modulus of spherical particles and the Macroscopic Young’s Modulus of particle packing layers. The “effective shear modulus” has expression the macroscopic modulus partially but not considered the affect of diameters of the spherical particles in those papers. When we study the sand and soil then looks them as granular mixtures, the “force chain” often as a important mechanism. The affect of the “force chain” is used in the lower stress and we should neglects it in the higher tension. We should attend to that the 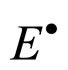 in formula 6 is only a process parameters and a constant, not the real Young’s Modulus of particle packing rock layers and no some good application meaning. In fact the Normal Contact Stiffness Kn is proportional to Macroscopic Young’s Modulus
in formula 6 is only a process parameters and a constant, not the real Young’s Modulus of particle packing rock layers and no some good application meaning. In fact the Normal Contact Stiffness Kn is proportional to Macroscopic Young’s Modulus 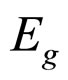 when only single contact point. The formula 5 be transformed into formula 7.
when only single contact point. The formula 5 be transformed into formula 7.
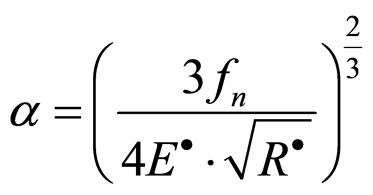 (7)
(7)
When we know the stress of external force which the particle packing rock layers suffered, calculating the derivative of the formula 7, My paper get the formula 8.
 (8)
(8)
The Macroscopic Young’s Modulus 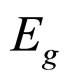 as formula 9 shows.
as formula 9 shows.
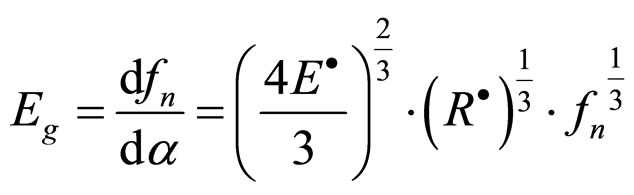 (9)
(9)
The formula 9 is the theoretical Macroscopic Young’s Modulus for arbitrary spherical particles contact for small deformation respectively. If that is equal diameter, equal Young’s Modulus, equal Poisson’s Ratio spherical particles, formula 9 can be transformed into formula 10.
 (10)
(10)
From those component in formula 10, we can find that the theoretical Macroscopic Young’s Modulus of particle packing rock layers mainly be effected by following parameters:
1) The material’s Young’s Modulus of spherical particles. The theoretical Macroscopic Young’s Modulus of particle packing rock layers is proportional to the material’s Young’s Modulus of spherical particles and inversely proportional to the material’s Poisson’s Ratio of spherical particles.
2) 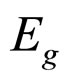 is proportional to
is proportional to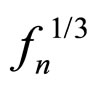 , so proportional to the depth and stress and can not be calculated by Hooke’s Law.
, so proportional to the depth and stress and can not be calculated by Hooke’s Law.
3) The material’s Young’s Modulus of spherical particles also be affected by temperature and pressure. Such as the material’s Young’s Modulus of sand particles (quartz) in the sandstone will decrease with higher temperature.
4. How the Arrangements of Particle Affected
In the unconsolidated sandstone formation, the normal contact external force fn of equal diameter spherical particles is related to the corresponding depth, principal stress, diameter of particles. The fn is the forces be decomposed by f in the Figure 2. Their has five types familiar arrangements modes of particles [6,8], their names and coordination number as table 1 shows and their figures of modes shows as Figure 2. The particle packing rock layers tend to transform to make the direction of Max ability of resistance contact force consistent with the direction of the maximum principal stress  (parallel to Z-axis in Figure 2). We may begins with the example that the
(parallel to Z-axis in Figure 2). We may begins with the example that the  is the maximum principal stress
is the maximum principal stress 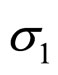 in a rock layer in a fault basin. The
in a rock layer in a fault basin. The 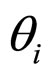 is the angle of force-decomposition. The force-decomposition of five types familiar arrangements modes as Figure 2 shows.
is the angle of force-decomposition. The force-decomposition of five types familiar arrangements modes as Figure 2 shows.
The relations between corresponding total normal contact force fn and 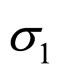 (parallel to Z-axis) of the particles arrangements modes i as formula 11 shows.
(parallel to Z-axis) of the particles arrangements modes i as formula 11 shows.
 (11)
(11)
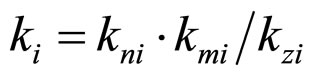 (12)
(12)
That the relations between the Macroscopic Young’s Modulus Eg and  of the particles arrangements modes i as formula 13 shows.
of the particles arrangements modes i as formula 13 shows.
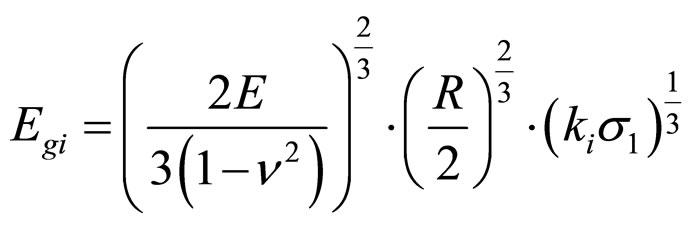 (13)
(13)
The 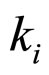 is the coefficient that can tell the relations between maximum principal stress
is the coefficient that can tell the relations between maximum principal stress 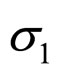 and its corresponding normal contact force fni of a single particle under the affect of the particles arrangements modes i.
and its corresponding normal contact force fni of a single particle under the affect of the particles arrangements modes i.
The kn is the area coefficient which express a single particle undertake the stress/theoretical area. kni is the area coefficient kn of the particles arrangements modes .
.
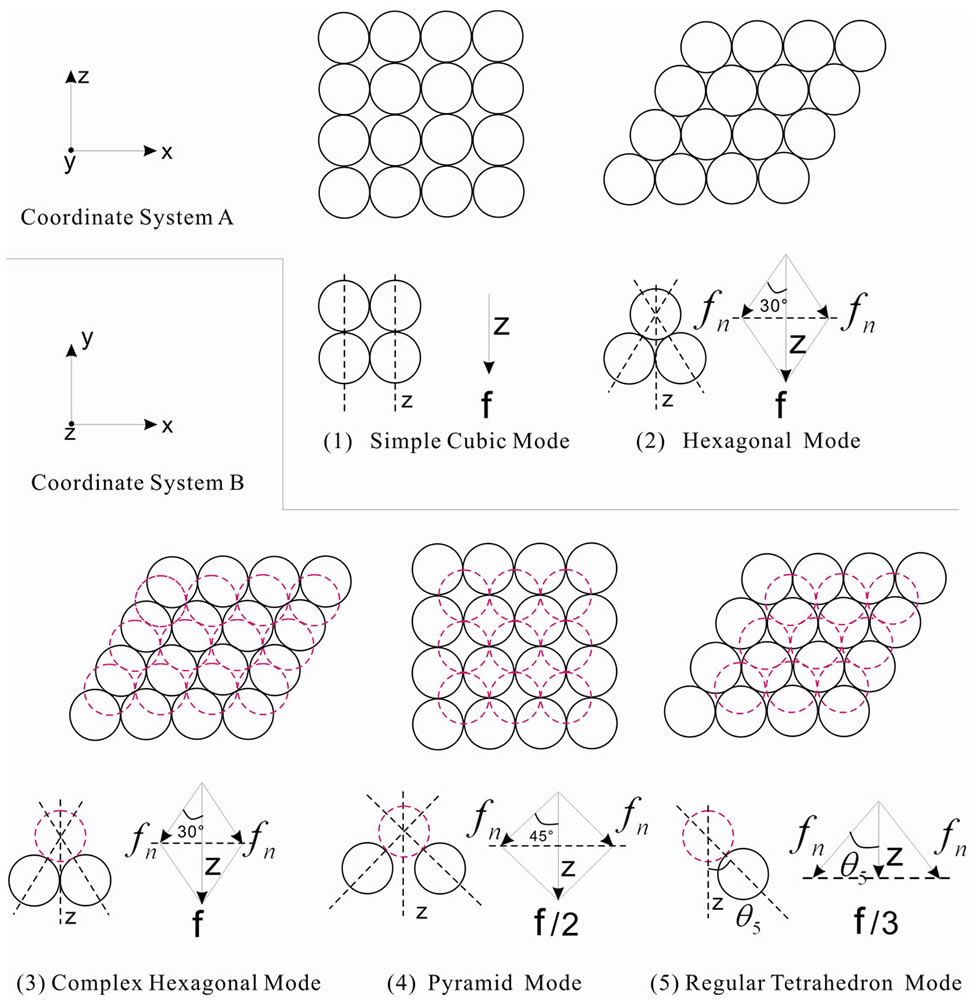
Figure 2. Five types familiar arrangements modes of particles (coordinate system B: The Z-axis perpendicular to the paper surface, 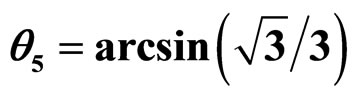 , (1) and (2) accord with the coordinate system A and the (3-5) accord with the coordinate system B, f is the force of σ1).
, (1) and (2) accord with the coordinate system A and the (3-5) accord with the coordinate system B, f is the force of σ1).

Table 1. coefficients of the five types familiar particles arrangements modes (the data of n, hi, vrh was come from reference [6]).
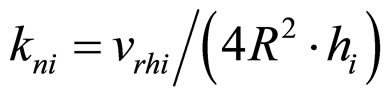 (14)
(14)
We can find that the f in Figure 2 accord with formula 15.
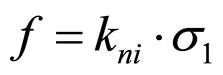 (15)
(15)
The km is the coefficient which express contact angle between the two layers particles, The kmi is the coefficient km of the particles arrangements modes i. The kz is a coefficient which relate to the coordination numbers N. The 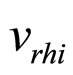 is the undertake volume of a single particle of the particles arrangements modes i. The hi is the layer height of the particles arrangements modes i.
is the undertake volume of a single particle of the particles arrangements modes i. The hi is the layer height of the particles arrangements modes i.
The kmi should be calculated according to the force decomposition angles 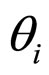 which based on the decomposition principle for the forces. The decomposition angles
which based on the decomposition principle for the forces. The decomposition angles 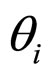 shows as Figure 2.
shows as Figure 2.
Besides the particles arrangements mode 1—the Simple Cubic Mode, the  (
( ) should be calculated according to the effective coordination number
) should be calculated according to the effective coordination number 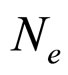 (
(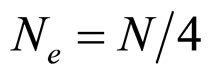 ).
).
Those coefficients of the 5 types familiar particles arrangements modes as the table 1 shows. If we sum and average the five types familiar particles arrangements modes simply. The sum and average can not representative the fact on the particle packing rock layers. But in a larger scale, the five familiar particles arrangements modes must all exist and closer to the average. The sum and average not means a bigger error. From the table 1, the coordination number 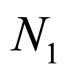 and vertical
and vertical 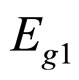 (
(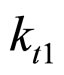 ) of the Simple Cubic Mode is smallest and the biggest of the Regular Tetrahedron Mode. Not all the coordination number undertake the maximum principal stress
) of the Simple Cubic Mode is smallest and the biggest of the Regular Tetrahedron Mode. Not all the coordination number undertake the maximum principal stress 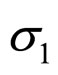 and the change of vertical
and the change of vertical 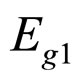 (
(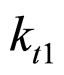 ) mild than the change of the coordination number
) mild than the change of the coordination number .
.
The model has not finished. Because model in above paragraphs focused on the contact force fni which parallel to the maximum principal stress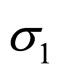 . When the normal contact force fni not parallel to the maximum principal stress
. When the normal contact force fni not parallel to the maximum principal stress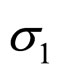 , we need to convert the normal displacements
, we need to convert the normal displacements  to parallel to the maximum principal stress
to parallel to the maximum principal stress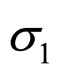 . So the
. So the 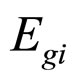 transform into the formula 16.
transform into the formula 16.
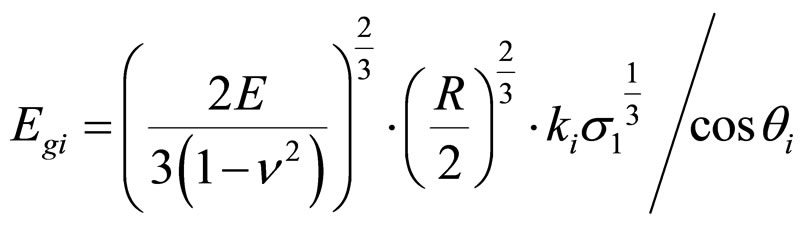 (16)
(16)
So, if look the 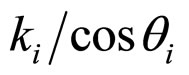 in formula 16 as a total coefficient kt, then the kti shows as table 1. If we sum and average the five familiar particles arrangements modes simply. Then the average kt must be (
in formula 16 as a total coefficient kt, then the kti shows as table 1. If we sum and average the five familiar particles arrangements modes simply. Then the average kt must be ( = 0.63538).
= 0.63538).
The formula 10 and the formula 16 is respectively the Eg that expressed by normal contact force fni and maximum principal stress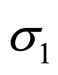 . The formula 16 tell us that the Eg is proportional to
. The formula 16 tell us that the Eg is proportional to .
.
Because differentiation of those material’s Young’s Modulus E of spherical particles is often not big, but the differentiation of the radius of particles R is often difference by several magnitudes. So the R is often the principal influencing factors of Eg and maybe lead to the Eg of sandstone bigger than that of mud rock.
In populous sedimentary basin and its most sedimentary stage, for example the loose sand particle packing layers in quaternary, in those layers, the principal stress in vertical direction 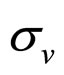 is the Max principal stress
is the Max principal stress , that is say that
, that is say that  parallel to Z-axis, the stress field is express as
parallel to Z-axis, the stress field is express as , the
, the 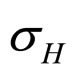 is the Max horizontal principal stress and the
is the Max horizontal principal stress and the 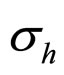 is the Min horizontal principal stress. In those type stress field,
is the Min horizontal principal stress. In those type stress field, 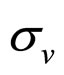 should be provided by the gravity of overlying strata S.
should be provided by the gravity of overlying strata S.
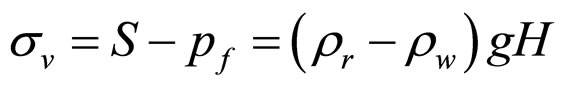 (17)
(17)
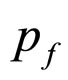 is the pore fluid pressure,
is the pore fluid pressure,  is the bulk density of spherical particles,
is the bulk density of spherical particles, 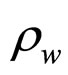 is the bulk density of pore fluid (often is water).
is the bulk density of pore fluid (often is water).
In practice, we can use the formula 17 to estimate the Max principal stress  in depth of H, then can we grasp the relations between the depth of H and the Macroscopic Young’s Modulus roughly.
in depth of H, then can we grasp the relations between the depth of H and the Macroscopic Young’s Modulus roughly.
5. Discussion
Young’s Modulus of quartz bulk parent rock is often 40 GPa - 100 GPa. In fact the quartz bulk parent rocks is also have pore and its Young’s Modulus is less than that of material’s of spherical sand particles. Other material's Young´s Modulus of material’s has hardly been reported before. Because of the existing of some other mineral particles and clay particles, Young’s Modulus of mineral particles maybe less than the quartz mineral particles, but maybe not less than the quartz bulk parent rock. LiuYu (2010) [7] thought that 20 GPa - 80 GPa is a reasonable range of Young’s Modulus of mineral particles E. Some data from Tian Jia-ning (1988) [9] tell that those Young’s Modulus of rocks distributed from 5 GPa - 60 GPa and very discrete. Those Young’s Modulus of some rocks of clay particles is only 0.17 Ga, this less two magnitudes than that of sandstones, and maybe related to the spatial structure of those clay particles. Some shear wave velocity of particles packing rock layers which not deep than 15 m is often only 60 - 200 m/s (Elnashai, 2008) [10] and far less than that of average value of sedimentary rock on the upper crust (2800 m/s - 3500 m/s), also less than the compressional wave velocity of water (1400 m/s). Some data from An-Ou (1992 [11]) also tell that the Young’s Modulus of rocks distributed from 0.1 GPa - 20 GPa and very discrete. Those bigger differentiation of Young’s Modulus and wave velocity verify that the Young’s Modulus tend to approaching to zero when close to earth surface synchronously.
The former model on Macroscopic Young’s Modulus of particle packing rock layers is only suitable for the rock layers not depth than several hundred meters or some loose sandstone with rapid sedimentation. Plastic deformation maybe the dominating mode of the change of Macroscopic Young’s Modulus of particle packing rock layers in a depth or an older stratum of rocks. In this paper, Eg is proportional to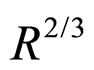 , but some data express that is inverse proportion, for example An-Ou (1992: p. 34) [11], The paper think that because of those data was come from rocks in depth and had undertake long-term plastic deformation and dynamic diagenesis. The plastic deformation velocity of little diameter particles is greater than that of the bigger diameter particles. The plastic deformation velocity model of particle packing rock layers need to be developed. We should also attend to that the instantaneous Young’s Modulus will determine the plastic deformation velocity in a time future .The elastic deformation will runs through modern and the elastic deformation model will be the basement to distinguish the elastic deformation and plastic deformation.
, but some data express that is inverse proportion, for example An-Ou (1992: p. 34) [11], The paper think that because of those data was come from rocks in depth and had undertake long-term plastic deformation and dynamic diagenesis. The plastic deformation velocity of little diameter particles is greater than that of the bigger diameter particles. The plastic deformation velocity model of particle packing rock layers need to be developed. We should also attend to that the instantaneous Young’s Modulus will determine the plastic deformation velocity in a time future .The elastic deformation will runs through modern and the elastic deformation model will be the basement to distinguish the elastic deformation and plastic deformation.
6. Conclusions
1) The paper set up a model to calculate the Macroscopic Young’s Modulus of particle packing rock layers and the model includes the model that can tell how the arrangements of particle affected.
2) 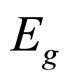 is proportional to
is proportional to  and proportional to
and proportional to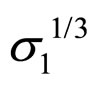 , can not be calculated by Hooke’s Law. The Macroscopic Young’s Modulus of dry sand particle packing rock layers which close to the earth surface is approaching to zero in 0 m depth, and the too little Macroscopic Young’s Modulus is the main cause of earthquake site effect.
, can not be calculated by Hooke’s Law. The Macroscopic Young’s Modulus of dry sand particle packing rock layers which close to the earth surface is approaching to zero in 0 m depth, and the too little Macroscopic Young’s Modulus is the main cause of earthquake site effect.
3)  is proportional to
is proportional to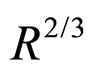 , the differentiation of the radius of particles R is often difference by several magnitudes. So the R is often the principal influencing factors of
, the differentiation of the radius of particles R is often difference by several magnitudes. So the R is often the principal influencing factors of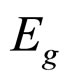 .
.
4) When equal stress, the increased of the coordination number lead to the decrease of the normal contact force , this lead to the coordination number is an inverse proportion to Macroscopic Young’s Modulus. But the larger coordination number change only means very little Macroscopic Young’s Modulus change.
, this lead to the coordination number is an inverse proportion to Macroscopic Young’s Modulus. But the larger coordination number change only means very little Macroscopic Young’s Modulus change.
REFERENCES
- X. Liu, “Elastic Parameters and Velocity Calculation in Multi-Phase Materials,” Ph.D. Thesis, Institute of Geophysics, Beijing, 2002, pp. 1-78.
- T.-D. Xia, Y. Liu, M. Wu, et al., “Shear Wave Velocity in Deep Buried Sand Based on Spheres-Contact Theory,” Journal of Harbin Institute of Technology, Vol. 43, 2011, pp. 99-103.
- X.-X. Zhong and J.-X. Yuan, “Microfabrics and Constitutive Relations of Granular Materials,” Chinese Journal of Geotechnical Engineering, Vol. 14, 1992, pp. 39-48.
- K. L. Johnson, “Contact Mechanics,” Cambridge University Press, Cambridge, 1985, pp. 91-104.
- M. Oda and K. Iwashita, “Mechanics of Granular of Granular Materials: An Introduction,” A. A. Balkema, Rotterdam, 1999, pp. 207-209.
- Q.-C. Sun, M.-Y. Hou, F. Jin, et al., “The Physical and Mechanical of Granular Materials,” Science Press, Beijing, 2011, pp. 191-193.
- Y. Liu, “Research on Sand Shear Wave Velocity Based on Particle Contact Model,” Ph.D. Thesis, Zhejiang University, Hangzhou, 2010, pp. 1-127.
- F. Zeng, et al., “Particle Technology of Mineral Processing,” China University of Mining Press, Xuzhou, 2001, pp. 92-93.
- J.-N. Tian and H.-L. Shi, “Comparison and Experimental Study of Dynamic Elastic Modulus and Tatic Modulus,” Journal of Hydro Electric Power, Vol. 4, 1988, pp. 21-27.
- A. S. Elnashai and L. D. Sarno, “Fundamentals of Earthquake Engineering,” Wiley, Hoboken, 2008, pp. 28-29.
- An-Ou, “Tectonic Stress Field,” Earthquake Publishing House, Beijing, 1992, pp. 1-60.
NOTES
*Corresponding author.

