Optics and Photonics Journal
Vol.2 No.3(2012), Article ID:22504,4 pages DOI:10.4236/opj.2012.23027
Break up of N-Soliton Bound State in a Gradient Refractive Index Waveguide with Nonlocal Nonlinearity
1Department of Mathematics, Faculty of Sciences, Brawijaya University, Malang, Indonesia
2Mathematics and Natural Sciences PhD Program, Airlangga University, Surabaya, Indonesia
3Department of Physics, Faculty of Sciences and Technology, Airlangga University, Surabaya, Indonesia
Email: isnanidarti@ub.ac.id
Received June 28, 2012; revised July 31, 2012; accepted August 10, 2012
Keywords: N-Soliton Bound State; GRIN Waveguide; Nonlocal Nonlinearity; Conserved Implicit Crank-Nicolson Method; Inverse Scattering Technique
ABSTRACT
We study the propagation of N-soliton bound state in a triangular gradient refractive index waveguide with nonlocal nonlinearity. The study is based on the direct numerical solutions of the model and subsequent eigenvalues evolution of the corresponding Zakharov-Shabat spectral problem. In the waveguide with local nonlinearity, the velocity of a single soliton is found to be symmetric around zero and therefore the soliton oscillates periodically inside the waveguide. If the nonlocality is presence in the medium, the periodic motion of soliton is destroyed due to the soliton experiences additional positive acceleration induced by the nonlocality. In the waveguide with the same strength of nonlocality, a higher amplitude soliton experiences higher nonlocality effects, i.e. larger acceleration. Based on this soliton behavior we predict the break up of N-soliton bound state into their single-soliton constituents. We notice that the splitting process does not affect the amplitude of each soliton component.
1. Introduction
The propagation of optical beam in a homogenous Kerr medium is described by the nonlinear Schrodinger (NLS) equation which has a soliton solution. Spatial solitons are self-trapped light beams in which the diffraction is balanced by the self-focusing induced by nonlinearity. In a homogeneous Kerr medium with local nonlinearity, a single soliton propagates with a constant velocity. The velocity of soliton is disturbed as it propagates in an inhomogeneous refractive index medium, i.e., a medium with a transverse gradient refractive index (GRIN) distribution, see e.g. [1,2]. If the nonlinear response of medium is nonlocal then it may significantly affect the properties of soliton [3]. For example, a uniform medium with positive nonlocal nonlinearity may induce a self-bending soliton [4-6]. It has been shown that a nonlocality increases the soliton acceleration. In a medium with the same strength of nonlocality, a higher amplitude soliton experiences much larger nonlocality effects than the lower one and therefore a soliton with higher amplitude will propagate with larger acceleration than that with lower amplitude, see e.g. [7,8].
It is known that the NLS equation has N-soliton bound state solution. Such a bound state contains N single solitons which have different amplitudes but they travel together with the same speed. During the propagation Nsoliton bound state undergoes periodic oscillations in shape with individual solitons remaining localized. It is noticed that N-soliton bound state has no binding energy and therefore under suitable perturbations the N-soliton bound state can break up into their soliton constituents [9]. The break up of spatial N-soliton bound state can be induced e.g. by reflection at material interface [10], refractive index variation [11,12], interaction with periodic lattice [13,14], combination of twoand three-photon absorption [15], linear loss [16], and defect layer [17]. In this paper we study the break up of N-soliton bound state in a triangular GRIN waveguide with nonlocal nonlinearity. The study is based on the direct numerical solutions of the modified nonlinear Schrödinger (m-NLS) equation as well as the evolution of discrete eigenvalues of the corresponding Zakharov-Shabat spectral problem. For that purposes in Section 2 we review the beam propagation equation in non-homogeneous medium with nonlocal nonlinearity as well as the inverse scattering theory. Then we study in Section 3 the propagation of a single soliton in a triangular waveguide. It is shown that when a single soliton is launched in a triangular waveguide then it experiences transverse acceleration which depends on the strength of nonlocality as well as on its amplitude. Using these propagation properties in Section 4 we study the break up of N-soliton bound state into multiple single soliton. Finally conclusion will be given in the last section.
2. Basic Equation and Inverse Scattering Technique
We consider the evolution of beam propagating along the z axis in a slab waveguide with inhomogeneous linear refractive index in a transverse direction and first-order nonlocal contribution to nonlinear respond. Such beam propagation is described by the normalized modified nonlinear Schrödinger (m-NLS) equation, see [18]:
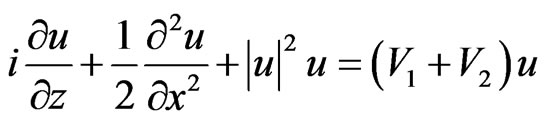 , (1)
, (1)
where  and
and 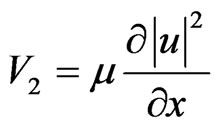 are respectively the contributions of linear refractive index inhomogeneity and nonlocality. Function
are respectively the contributions of linear refractive index inhomogeneity and nonlocality. Function 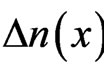 and parameter
and parameter 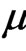 denote the profile of GRIN distribution and the strength of the nonlocal component of nonlinear response, respectively. The GRIN distribution in this paper is considered to have a triangular profile,
denote the profile of GRIN distribution and the strength of the nonlocal component of nonlinear response, respectively. The GRIN distribution in this paper is considered to have a triangular profile,
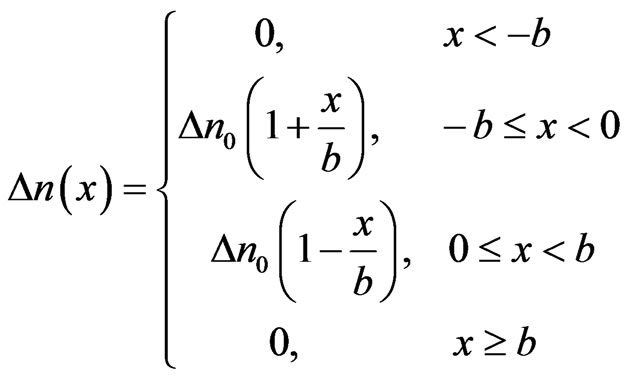 , (2)
, (2)
where 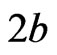 is the total width of the waveguide and
is the total width of the waveguide and 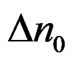 is the maximum index variation. Notice that the waveguide is symmetric where its center is located at
is the maximum index variation. Notice that the waveguide is symmetric where its center is located at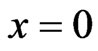 . In the absence of inhomogeneity and nonlocality, i.e.
. In the absence of inhomogeneity and nonlocality, i.e.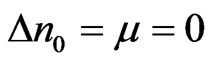 , Equation (1) is known as the NLS equation. The NLS equation is integrable by the inverse scattering technique (IST) [19]. In this approach, the NLSE is associated with the Zakharov-Shabat eigenvalue problem (ZSEP),
, Equation (1) is known as the NLS equation. The NLS equation is integrable by the inverse scattering technique (IST) [19]. In this approach, the NLSE is associated with the Zakharov-Shabat eigenvalue problem (ZSEP),
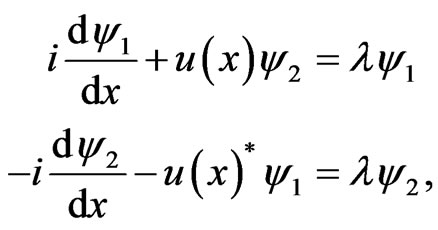 , (3)
, (3)
where u is the beam envelope which acts as potential function and superscript * denotes the complex conjugate. If the linear z-evolution of the auxiliary spectral function  is given then the NLS equation can be resolved from the compatibility condition
is given then the NLS equation can be resolved from the compatibility condition . The continuous spectrum of ZSEP corresponds to waves that are radiated away; whereas a number of discrete eigenvalues
. The continuous spectrum of ZSEP corresponds to waves that are radiated away; whereas a number of discrete eigenvalues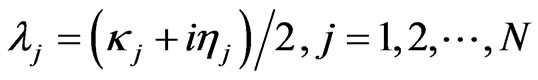 corresponds to N soliton. Here
corresponds to N soliton. Here  and
and 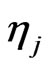 define the velocity and the amplitude of the j-th soliton, respectively [20]. One of particular N-soliton is obtained if we consider an initial scattering potential
define the velocity and the amplitude of the j-th soliton, respectively [20]. One of particular N-soliton is obtained if we consider an initial scattering potential
 . (4)
. (4)
Satsuma and Yajima [21] showed that ZSEP (3) with initial potential (4) has eigenvalues which are purely imaginary
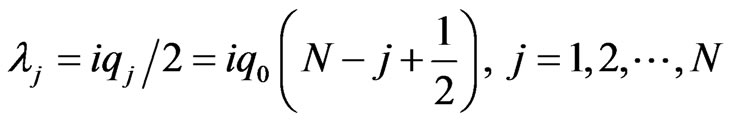 . (5)
. (5)
This solution is called an N-soliton bound state or higher-order soliton because it contains N single soliton components which propagate together and always remain localized in x (the transversal velocity of each single soliton is zero, i.e.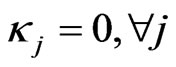 ).
).
In the absence of perturbations (e.g. linear refractive index variation and nonlocality) to the NLS equation, the ZSEP is iso-spectral (all eigenvalues are constant). In other words, the soliton content of a given input remains constant. In the presence of perturbations, the soliton eigenvalues are no longer z-invariant and the m-NLSE is not integrable and therefore the IST cannot be applied. However the ZSEP provide a powerful tool which enables us to monitor the dynamics of the discrete eigenvalues, i.e. the parameters of each individual soliton. In this case, when analyzing a certain potential (beam shape) at a distance z, the obtained discrete eigenvalues gives information about the soliton as if it would further propagate in an unperturbed medium. As long as the perturbations are small, the ZSEP holds likewise in the perturbed medium. In this paper, the soliton eigenvalues of the ZSEP will be determined numerically using procedure given in [22]. For this purpose, the potential 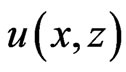 at distance z is obtained by solving the m-NLS equation using the conserved implicit Crank-Nicolson scheme [23].
at distance z is obtained by solving the m-NLS equation using the conserved implicit Crank-Nicolson scheme [23].
3. Propagation of a Single Soliton
We begin with the propagation of a single soliton in a triangular GRIN waveguide by considering an input beam as in Equation (4) with N = 1,  and initial position at
and initial position at . First we use waveguide parameters to be
. First we use waveguide parameters to be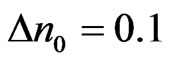 ,
, 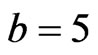 ,
, 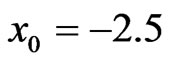 and some values of
and some values of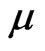 . Figures 1(a)-(c) show the evolution of beam envelope for μ = 0, 0.01, 0.02 respectively. The corresponding eigenvalue evolutions are depicted in Figures 1(d)-(f) (imaginary parts/
. Figures 1(a)-(c) show the evolution of beam envelope for μ = 0, 0.01, 0.02 respectively. The corresponding eigenvalue evolutions are depicted in Figures 1(d)-(f) (imaginary parts/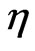 ) and Figures 1(g)-(i) (real parts/
) and Figures 1(g)-(i) (real parts/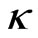 ). It is shown that during the evolution, the imaginary part of eigenvalue (
). It is shown that during the evolution, the imaginary part of eigenvalue (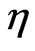 ) in all three cases is almost constant; indicating that the change of soliton amplitude during its
) in all three cases is almost constant; indicating that the change of soliton amplitude during its
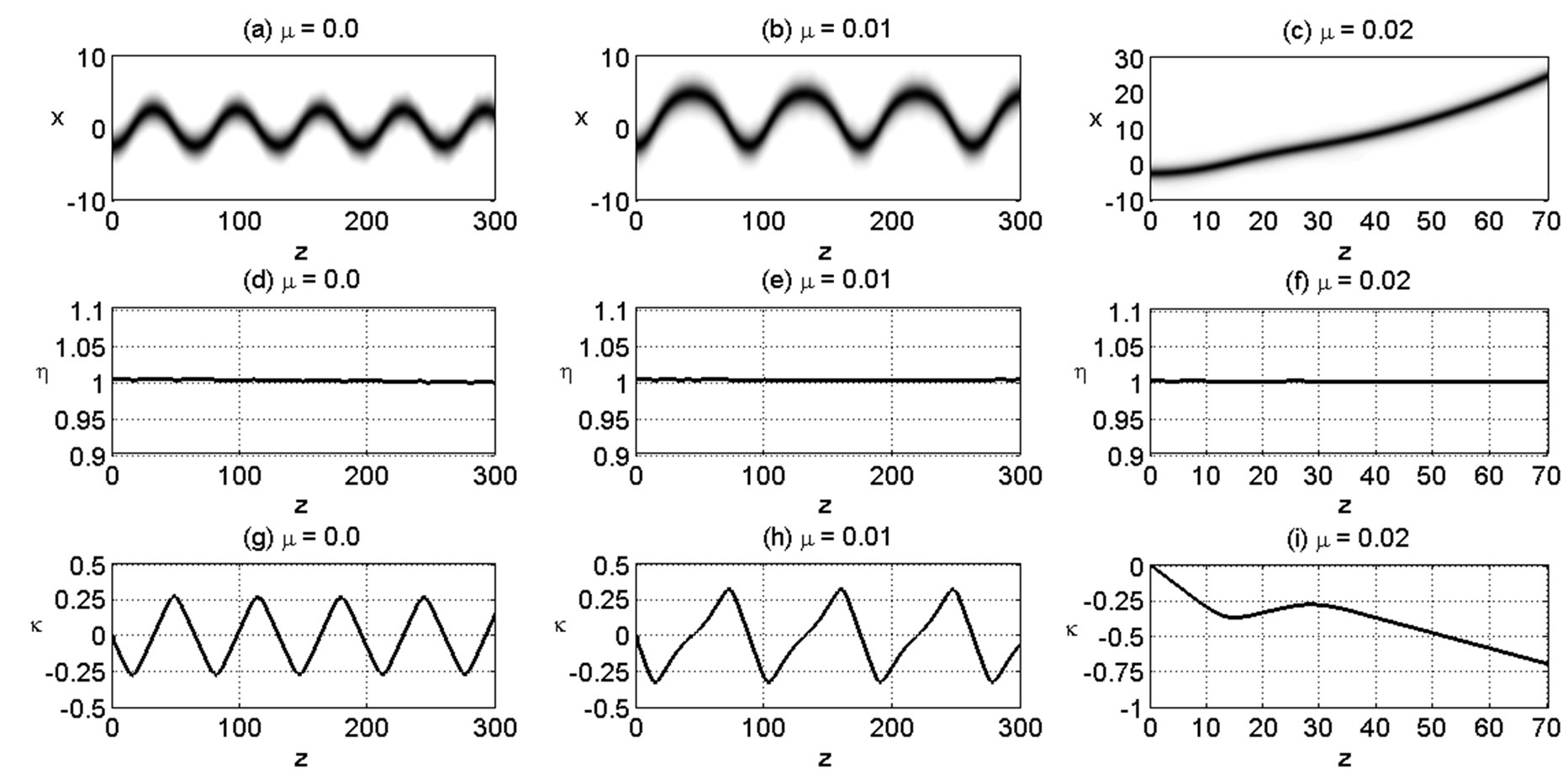
Figure 1. Propagation of a soliton with amplitude  and initial position
and initial position  in a triangular GRIN waveguide with
in a triangular GRIN waveguide with 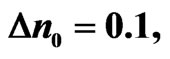
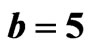 . The first row shows the evolution of beam envelope for (a)
. The first row shows the evolution of beam envelope for (a)  (b)
(b) 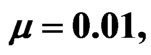 and (c)
and (c)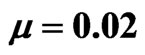 . Dynamics evolution of the corresponding eigenvalue is shown in the second and third rows for the imaginary part and the real part of eigenvalue, respectively.
. Dynamics evolution of the corresponding eigenvalue is shown in the second and third rows for the imaginary part and the real part of eigenvalue, respectively.
propagation is small. However, the real part of the eigenvalue (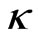 ) is certainly not invariant. If the nonlinearity of medium is local (
) is certainly not invariant. If the nonlinearity of medium is local (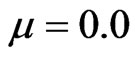 ) then the real part of eigenvalue (
) then the real part of eigenvalue (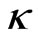 ) is a symmetric function around zero. This behavior shows that during the propagation the soliton oscillates symmetrically around the center of waveguide. In the medium with
) is a symmetric function around zero. This behavior shows that during the propagation the soliton oscillates symmetrically around the center of waveguide. In the medium with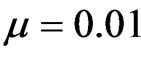 , the changing of
, the changing of 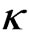 is faster and bigger; meaning that the soliton experiences a larger acceleration. Nevertheless the soliton still oscillates but asymmetrically about the waveguide center. The effect of nonlocality is more pronounced if we further increase the nonlocality. Indeed, by taking
is faster and bigger; meaning that the soliton experiences a larger acceleration. Nevertheless the soliton still oscillates but asymmetrically about the waveguide center. The effect of nonlocality is more pronounced if we further increase the nonlocality. Indeed, by taking , we see that the soliton propagates with much larger acceleration such that
, we see that the soliton propagates with much larger acceleration such that 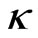 does not oscillate anymore. Here
does not oscillate anymore. Here  is always negative which means that the soliton always experiences positive velocity. It can be said that the waveguide does not support the oscillating soliton. Instead, the soliton is forced to exit the waveguide. Outside the waveguide, i.e. when
is always negative which means that the soliton always experiences positive velocity. It can be said that the waveguide does not support the oscillating soliton. Instead, the soliton is forced to exit the waveguide. Outside the waveguide, i.e. when 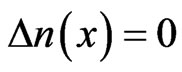 the soliton propagates with a constant acceleration (or linear velocity). We remark that the eigenvalues evolution perfectly matched with the equivalent particle approach in [8].
the soliton propagates with a constant acceleration (or linear velocity). We remark that the eigenvalues evolution perfectly matched with the equivalent particle approach in [8].
Next we study the effect of soliton amplitude on its propagation in nonlocal triangular GRIN waveguide with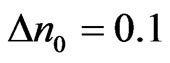 ,
,  ,
,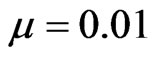 and
and 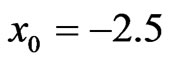 by varying
by varying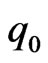 , see Figure 2. In Figure 2(a) we show the propagation of soliton with
, see Figure 2. In Figure 2(a) we show the propagation of soliton with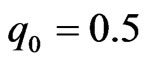 . It is noticed that in this case the waveguide width is narrower than the soliton width and the index variation is sufficiently large. Consequently, part of soliton which is inside the waveguide will move faster to the wave center while another part remains outside the waveguide. Therefore the soliton is distorted and emits some radiation during its propagation. However it is clearly seen that the main part still oscillates in the waveguide. Such radiation is also described by the evolution of imaginary part of its eigenvalue (
. It is noticed that in this case the waveguide width is narrower than the soliton width and the index variation is sufficiently large. Consequently, part of soliton which is inside the waveguide will move faster to the wave center while another part remains outside the waveguide. Therefore the soliton is distorted and emits some radiation during its propagation. However it is clearly seen that the main part still oscillates in the waveguide. Such radiation is also described by the evolution of imaginary part of its eigenvalue (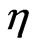 ); see Figure 2(d). Here the value of
); see Figure 2(d). Here the value of 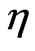 decreases which means that the soliton amplitude is getting smaller due to emitting radiation. The oscillation of the main part of beam is clearly seen from the real part of its eigenvalue (
decreases which means that the soliton amplitude is getting smaller due to emitting radiation. The oscillation of the main part of beam is clearly seen from the real part of its eigenvalue (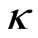 ); see Figure 2(g). We notice that the soliton in this case is not a single entity and therefore the equivalent particle approach presented in [8] cannot be applied. Figures 2(b)-(c) show that if we increase the soliton amplitude and therefore the soliton width is comparable to the width of waveguide then we hardly observe radiation during its propagation. This fact can also be seen from Figures 2(e)-(f) which show that each real part of its eigenvalue is practically speaking constant. However, we observed from Figures 2(h)-(i) that different amplitude soliton experiences different velocity. As mentioned in previous paragraph, the transversal velocity (
); see Figure 2(g). We notice that the soliton in this case is not a single entity and therefore the equivalent particle approach presented in [8] cannot be applied. Figures 2(b)-(c) show that if we increase the soliton amplitude and therefore the soliton width is comparable to the width of waveguide then we hardly observe radiation during its propagation. This fact can also be seen from Figures 2(e)-(f) which show that each real part of its eigenvalue is practically speaking constant. However, we observed from Figures 2(h)-(i) that different amplitude soliton experiences different velocity. As mentioned in previous paragraph, the transversal velocity (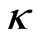 ) of soliton with amplitude
) of soliton with amplitude 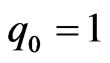 oscillates around zero and therefore the soliton also oscillates around the waveguide center. In the case of larger amplitude (
oscillates around zero and therefore the soliton also oscillates around the waveguide center. In the case of larger amplitude (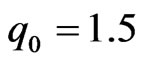 ), the soliton experiences much larger acceleration such that the transversal velocity is always positive (or
), the soliton experiences much larger acceleration such that the transversal velocity is always positive (or 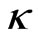 is always negative). Therefore the soliton always moves to the right and exit from the waveguide. This behavior is in accordance with the prediction of equivalent particle theory given in [8].
is always negative). Therefore the soliton always moves to the right and exit from the waveguide. This behavior is in accordance with the prediction of equivalent particle theory given in [8].
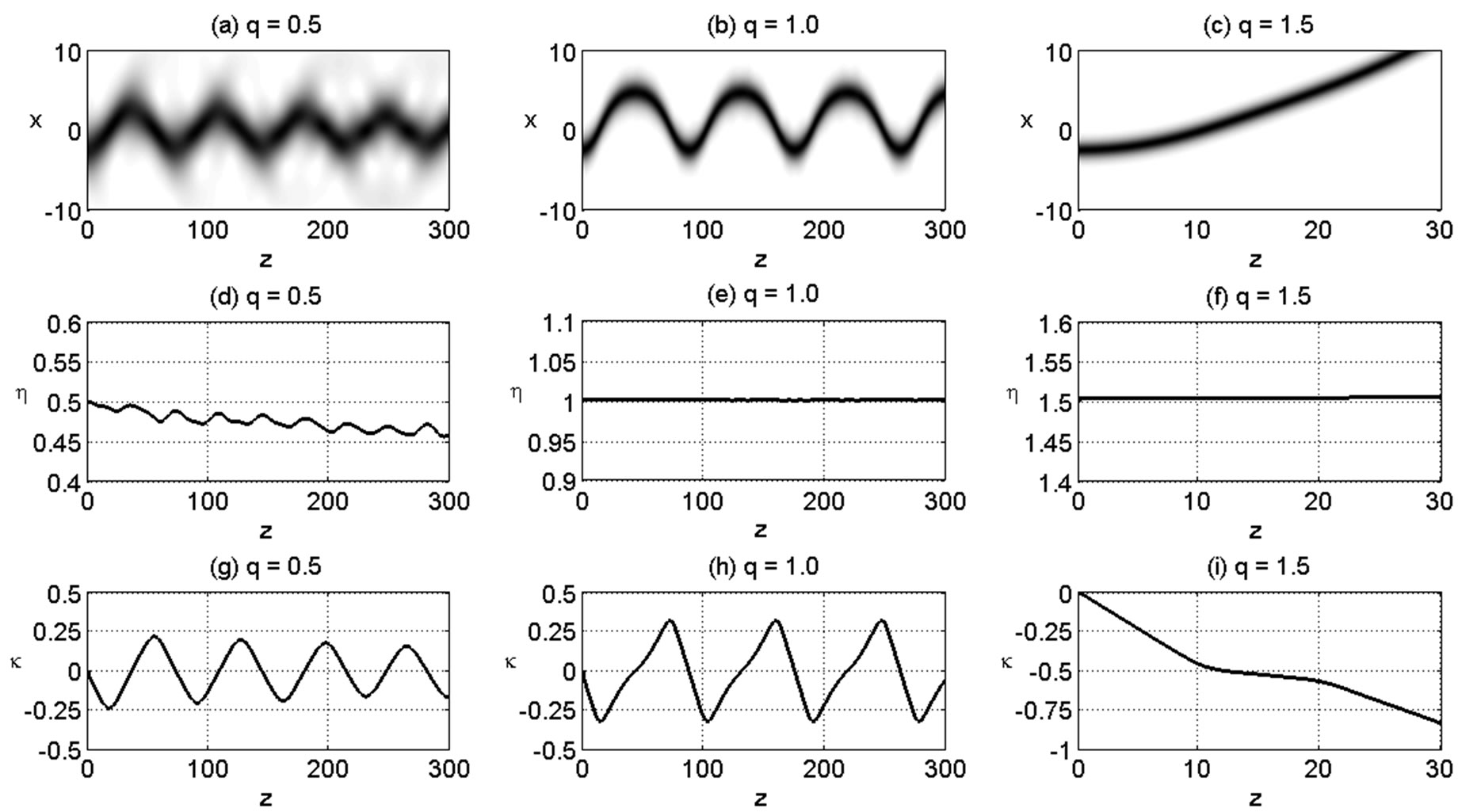
Figure 2. Propagation of a soliton with initial position 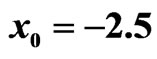 in a nonlocal triangular GRIN waveguide with
in a nonlocal triangular GRIN waveguide with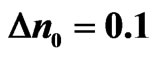 ,
, 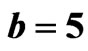 and
and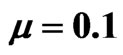 . The first row shows the evolution of beam envelope for (a)
. The first row shows the evolution of beam envelope for (a) 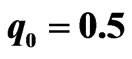 (b)
(b) 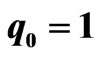 and (c)
and (c)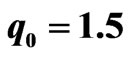 . Dynamics evolution of the corresponding eigenvalue is shown in the second and third rows for the imaginary part and the real part of eigenvalue, respectively.
. Dynamics evolution of the corresponding eigenvalue is shown in the second and third rows for the imaginary part and the real part of eigenvalue, respectively.
4. Break up of N-Soliton Bound State
We continue with the dynamics of the beam evolution when the input contains several single solitons. As discussed in previous section, different strength of nonlocality causes different transversal velocity of soliton. Moreover, in the waveguide with the same strength of nonlocality, a single soliton with different amplitude also experiences different velocity (–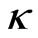 ). Hence, if the input beam is N-soliton bound state which consists of several single soliton with different amplitude then the bound state will certainly be destroyed because each soliton component experience different velocity. In other words the bound N-soliton bound state will break up when it propagates in a triangular GRIN waveguide with nonlocal nonlinearity. To illustrate the break up we perform several numerical experiments using initial condition given by Equation (4) with N = 2. The waveguide parameters are
). Hence, if the input beam is N-soliton bound state which consists of several single soliton with different amplitude then the bound state will certainly be destroyed because each soliton component experience different velocity. In other words the bound N-soliton bound state will break up when it propagates in a triangular GRIN waveguide with nonlocal nonlinearity. To illustrate the break up we perform several numerical experiments using initial condition given by Equation (4) with N = 2. The waveguide parameters are 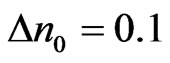 and
and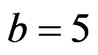 . In Figure 3 we show some numerical results using
. In Figure 3 we show some numerical results using  and
and  for three different values of
for three different values of . Notice that the input beam initially consists of two single solitons of amplitude
. Notice that the input beam initially consists of two single solitons of amplitude 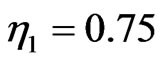 and
and 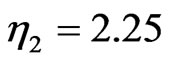 with zero velocity. It is seen from Figure 3 that during the evolution in the waveguide with
with zero velocity. It is seen from Figure 3 that during the evolution in the waveguide with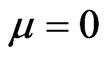 ,
, 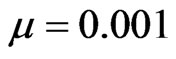 and
and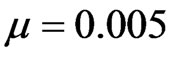 , each imaginary part of eigenvalues (
, each imaginary part of eigenvalues (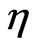 ) which corresponds to the amplitude of single solitons is relatively constant. This fact shows that the break up process almost does not affect the soliton amplitude. But each real part of eigenvalues changes immediately after the bound state enters the waveguide. The break up process can be considered as an interaction of two single solitons moving with different velocity. Due to this interaction, the velocity of each soliton certainly differs from that of a single soliton propagating alone. In the waveguide with local nonlinearity (
) which corresponds to the amplitude of single solitons is relatively constant. This fact shows that the break up process almost does not affect the soliton amplitude. But each real part of eigenvalues changes immediately after the bound state enters the waveguide. The break up process can be considered as an interaction of two single solitons moving with different velocity. Due to this interaction, the velocity of each soliton certainly differs from that of a single soliton propagating alone. In the waveguide with local nonlinearity ( ), after bound state breaks up into two solitons, each soliton constituent oscillates in the waveguide with different period. Since they have different oscillation period, a collision of the two solitons will certainly be predicted. The collision forces the smaller soliton (
), after bound state breaks up into two solitons, each soliton constituent oscillates in the waveguide with different period. Since they have different oscillation period, a collision of the two solitons will certainly be predicted. The collision forces the smaller soliton (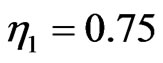 ) to exit the waveguide and then continue to propagate in the left side of waveguide with constant velocity. The higher soliton (
) to exit the waveguide and then continue to propagate in the left side of waveguide with constant velocity. The higher soliton ( ) in this case remains oscillating inside the waveguide. We further observe in Figure 3 that the increasing strength of nonlocality (
) in this case remains oscillating inside the waveguide. We further observe in Figure 3 that the increasing strength of nonlocality (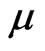 ) leads to much larger velocity of soliton with higher amplitude (
) leads to much larger velocity of soliton with higher amplitude (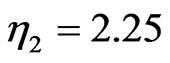 ) and therefore speeds up the splitting process of bound soliton. As a result, the higher amplitude soliton (
) and therefore speeds up the splitting process of bound soliton. As a result, the higher amplitude soliton (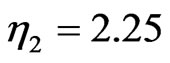 ) exits and propagates to the right part of the waveguide while the lower amplitude soliton (
) exits and propagates to the right part of the waveguide while the lower amplitude soliton (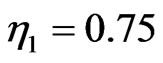 ) oscillates inside the waveguide.
) oscillates inside the waveguide.
To see the effects of amplitude and initial position of soliton, we plot some results of numerical simulations using the same parameters as in Figure 3 except 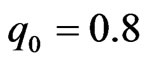 and three different initial positions; see Figure 4. Since N = 2 and
and three different initial positions; see Figure 4. Since N = 2 and , our initial beam consists of two single solitons with amplitude
, our initial beam consists of two single solitons with amplitude 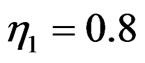 and
and 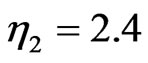
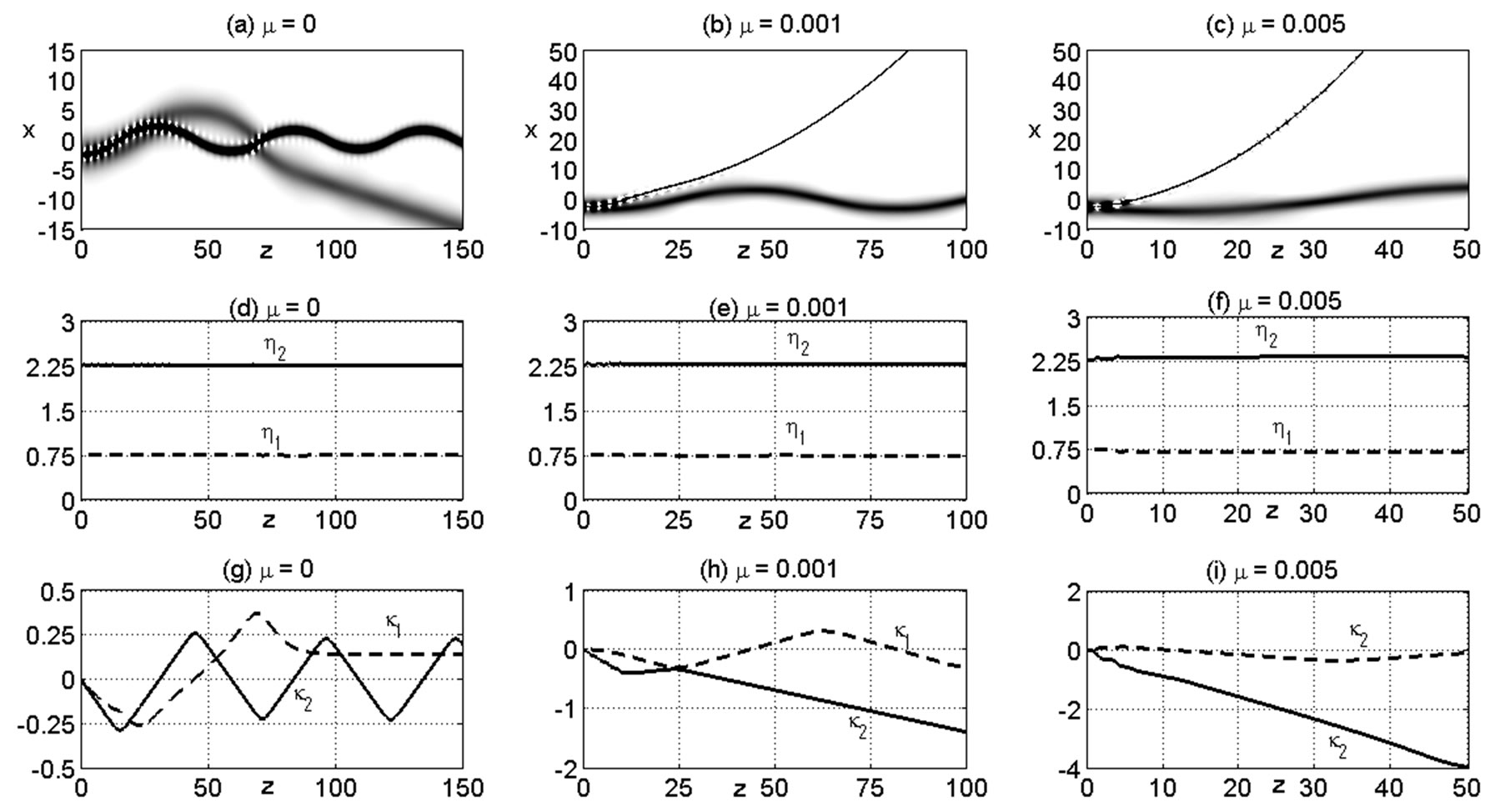
Figure 3. Break up of 2-soliton bound state in a triangular GRIN waveguide with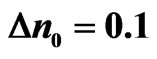 ,
,  , where the initial position of bound state is
, where the initial position of bound state is 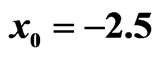 and
and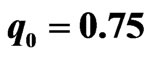 . The first row shows the evolution of beam envelope for (a)
. The first row shows the evolution of beam envelope for (a)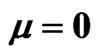 , (b)
, (b) 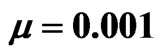 and (c)
and (c)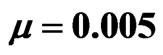 . Dynamics evolution of the corresponding eigenvalue is shown in the second and third rows for the imaginary part and the real part of eigenvalue, respectively.
. Dynamics evolution of the corresponding eigenvalue is shown in the second and third rows for the imaginary part and the real part of eigenvalue, respectively.

Figure 4. Break up of 2-soliton bound state with 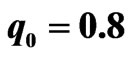 in a triangular GRIN waveguide with
in a triangular GRIN waveguide with ,
,  and
and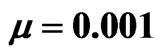 . The first row shows the evolution of beam envelope for three different initial positions, i.e. (a)
. The first row shows the evolution of beam envelope for three different initial positions, i.e. (a) , (b)
, (b) 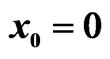 and (c)
and (c)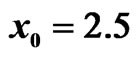 . Dynamics evolution of the corresponding eigenvalue is shown in the second and third rows for the imaginary part and the real part of eigenvalue, respectively.
. Dynamics evolution of the corresponding eigenvalue is shown in the second and third rows for the imaginary part and the real part of eigenvalue, respectively.
respectively, see Equations (3) and (4). Using 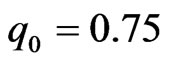 and
and 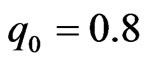 with the same initial position, we observe that these two cases give the same qualitative break up process of N-soliton bound state; see Figures 3(b), (e) and (h) and Figures 4(a), (d) and (g). Here the lower soliton oscillates inside the waveguide while the higher soliton exits from the waveguide. However, detail observation shows that soliton with amplitude
with the same initial position, we observe that these two cases give the same qualitative break up process of N-soliton bound state; see Figures 3(b), (e) and (h) and Figures 4(a), (d) and (g). Here the lower soliton oscillates inside the waveguide while the higher soliton exits from the waveguide. However, detail observation shows that soliton with amplitude 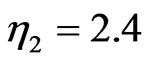 has larger velocity or acceleration (see Figures 4(a)-(g)) than that with amplitude
has larger velocity or acceleration (see Figures 4(a)-(g)) than that with amplitude 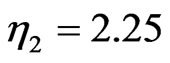 (see Figures 3(b)-(h)). This is caused by the fact that the higher amplitude soliton experiences larger nonlocality effect. If the initial position of bound state is shifted to the waveguide center, i.e. at
(see Figures 3(b)-(h)). This is caused by the fact that the higher amplitude soliton experiences larger nonlocality effect. If the initial position of bound state is shifted to the waveguide center, i.e. at  we see that the break up process is also qualitatively the same as if the bound state is initially placed at
we see that the break up process is also qualitatively the same as if the bound state is initially placed at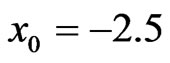 . But the break up process of bound state with initial position
. But the break up process of bound state with initial position 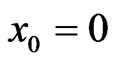 is slower than that with
is slower than that with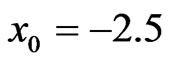 . Different splitting process is obtained if the initially position of bound state is at
. Different splitting process is obtained if the initially position of bound state is at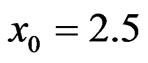 , see Figure 4(c). Although the higher soliton (
, see Figure 4(c). Although the higher soliton (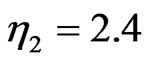 ) experiences larger velocity but it does not exit the triangular GRIN waveguide. In this case both solitons oscillate inside the waveguide with different period and therefore they experience consecutive collisions. We see that the consecutive collisions of two solitons is almost periodically and there is no soliton moving out from the waveguide until the propagation distance z = 200. This behavior can be seen clearly from the evolution of beam envelope in Figure 4(c) as well as from the velocity (–
) experiences larger velocity but it does not exit the triangular GRIN waveguide. In this case both solitons oscillate inside the waveguide with different period and therefore they experience consecutive collisions. We see that the consecutive collisions of two solitons is almost periodically and there is no soliton moving out from the waveguide until the propagation distance z = 200. This behavior can be seen clearly from the evolution of beam envelope in Figure 4(c) as well as from the velocity (–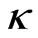 ) in Figure 4(i).
) in Figure 4(i).
5. Conclusion
We have investigated numerically the splitting of N-soliton bound state in a waveguide with nonlocal nonlinearity where the linear refractive index has a triangular profile. The splitting of N-soliton bound state is caused by the fact that each soliton components of the bound state experiences different acceleration induced by both refracttive index variation and nonlocal nonlinearity. It is also found that the splitting process of the N-soliton bound state does not affect the amplitude of all single soliton components.
6. Acknowledgements
This research is supported by Direktorat Penelitian dan Pengabdian kepada Masyarakat, Direktorat Jenderal Pendidikan Tinggi Indonesia (Penelitian Unggulan Perguruan Tinggi—Hibah Doktor via DIPA (RM) Universitas Airlangga SK No. 2613/H3/KR/2012, No. Kontrak 4074/ H3.6/PPd/2012).
REFERENCES
- S. H. Crutcher, A. J. Osei and M. E. Edwards, “Optical Spatial Solitons, the Power Law, and the Swing Effect,” Proceedings of SPIE, Vol. 7056, 2008, Article ID: 70560Q. Udoi:10.1117/12.792007U
- M. Ebnali-Heidari, M. K. Moravvej-Farshi and A. Zarifkar, “Swing Effect of Spatial Solitons Propagating through Gaussian and Triangular Waveguides,” Applied Optics, Vol. 48, No. 26, 2009, pp. 5005-5014. HUdoi:10.1364/AO.48.005005U
- W. Krolikowski and O. Bang, “Solitons in Nonlocal Nonlinear Media: Exact Solutions,” Physical Review E, Vol. 63, No. 1, 2000, Article ID: 016610. HUdoi:10.1103/PhysRevE.63.016610U
- V. Aleshkevich, Y. Kartashov and V. Vysloukh, “SelfBending of the Coupled Spatial Soliton Pairs in a Photorefractive Medium with Drift and Diffusion Nonlinearity,” Physical Review E, Vol. 63, No. 1, 2000, Article ID: 016603. Hdoi:10.1103/PhysRevE.63.016603U
- J. Petter, C. Weilnau, C. Denz, A. Stepken and F. Kaiser, “Self-Bending of Photorefractive Solitons,” Optics Communications, Vol. 170, No. 4, 1999, pp. 291-297. HUdoi:10.1016/S0030-4018(99)00485-XU
- Y. V. Izdebskaya, V. G. Shvedov, A. S. Desyatnikov, W. Krolikowski and Y. S. Kivshar, “Soliton Bending and Routing Induced by Interaction with Curved Surfaces in Nematic Liquid Crystals,” Optics Letters, Vol. 35, No. 10, 2010, pp. 1692-1694. HUdoi:10.1364/OL.35.001692U
- A. Suryanto and I. Darti, “Soliton Steering in a Ramp Waveguide with Nonlocal Nonlinearity,” Journal Nonlinear Optical Physics and Materials, Vol. 20, No. 1, 2011, pp. 33-41. HUdoi:10.1142/S0218863511005826U
- A. Suryanto and I. Darti, “Dynamics of Spatial Soliton in a Gradient Refractive Index Waveguide with Nonlocal Nonlinearity,” International Journal of Applied Mathematics and Statistics, Vol. 28, No. 4, 2012, pp. 23-30. http://www.ceser.in/ceserp/index.php/ijamas/article/view/1337
- S. V. Manakov, S. P. Novikov, L. P. Pitaevskii and V. E. Zakharov, “Theory of Solitons,” Consultants Bureu, New York, 1984.
- V. A. Aleshkevich, Y. V. Kartashov, A. S. Zelenina, V. A. Vysloukh, J. P. Torres and L. Torner, “Eigenvalue Control and Switching by Fission of Multisoliton Bound States in Planar Waveguides,” Optics Letters, Vol. 29, No. 5, 2004, pp. 483-485. HUdoi:10.1364/OL.29.000483U
- A. Suryanto and E. van Groesen, “Break up of Bound-NSpatial-Soliton in a Ramp Waveguide,” Optical Quantum Electronics, Vol. 34, No. 5, 2002, pp. 597-606. HUdoi:10.1023/A:1015685122513U
- A. Suryanto and E. van Groesen, “Self-Splitting of Multisoliton Bound States in Planar Waveguides,” Optics Communications, Vol. 258, No. 2, 2006, pp. 264-274. HUdoi:10.1016/j.optcom.2005.07.063U
- K. Zhou, Z. Guo and S. Liu, “Position Dependent Splitting of Bound States in Periodic Photonic Lattices,” Journal of the Optical Society of America B, Vol. 27, No. 5, 2010, pp. 1099-1103. HUdoi:10.1364/JOSAB.27.001099U
- Y. V. Kartashov, L. C. Crasovan, A. S. Zelenina, V. A. Vysloukh, A. Sanpera, M. Lewenstein and L. Torner, “Soliton Eigenvalue Control in Optical Lattices,” Physical Review Letters, Vol. 93, No. 14, 2004, Article ID: 143902. HUdoi:10.1103/PhysRevLett.93.143902U
- O. Katz, Y. Lahini and Y. Silberberg, “Multiple Break up of High-Order Spatial Soliton,” Optics Letters, Vol. 33, No. 23, 2008, pp. 2830-2832. HUdoi:10.1364/OL.33.002830U
- J. E. Prilepsky and S. A. Derevyanko, “Breakup of a Multisoliton State of the Linearly Damped Nonlinear Schrodinger Equation,” Physical Review E, Vol. 75, No. 3, 2007, Article ID: 036616. HUdoi:10.1103/PhysRevE.75.036616U
- S. Pu, C. Hou, K. Zhan, C. Yuan and Y. Du, “Spatial Solitons in Nonlocal Materials with Defocusing Effects,” Optics Communications, Vol. 285, No. 6, 2012, pp. 1456- 1460. HUdoi:10.1016/j.optcom.2011.11.037U
- Y. V. Kartashov, V. A. Vysloukh and L. Torner, “Tunable Soliton Self-Bending in Optical Lattices with Nonlocal Nonlinearity,” Physical Review Letter, Vol. 93, No. 15, 2004, Article ID: 153903. HUdoi:10.1103/PhysRevLett.93.153903U
- V. E. Zakharov and A. B. Shabat, “Exact Theory of TwoDimensional Self-Focusing and One-Dimensional Self-Modulation of Waves in Nonlinear Media,” Journal of Experimental and Theoretical Physics, Vol. 34, No. 1, 1972, pp. 62-69. http://www.jetp.ac.ru/cgi-bin/e/index/e/34/1/p62?a=list
- A. Hasegawa and Y. Kodama, “Solitons in Optical Communications,” Clarendon Press, Oxford, 1995.
- J. Satsuma and N. Yajima, “Initial Value Problems of One-Dimensional Self-Modulation of Nonlinear Waves in Dispersive Media,” Progress of Theoretical Physics Supplement, No. 55, 1974, pp. 284-306.
- P. Chamorro-Posada, G. S. McDonald, G. H. C. New and F. J. Fraile-Pelaez, “Fast Algorithm for the Evolution of Optical Solitons under Perturbations,” IEEE Transactions on Magnetics, Vol. 35, No. 3, 1999, pp. 1558-1561. HUdoi:10.1109/20.767268U
- I. Darti, Suhariningsih, Marjono and A. Suryanto, “A Conservative Finite Difference Scheme for Simulation of Soliton in Inhomogeneous Medium with Nonlocal Nonlinearity,” International Journal of Mathematics and Computation, Vol. 13. No. D11, 2011, pp. 69-77. www.ceser.in/ceserp/index.php/ijmc/article/view/1153

