Journal of Surface Engineered Materials and Advanced Technology
Vol.2 No.1(2012), Article ID:16999,6 pages DOI:10.4236/jsemat.2012.21009
Analytical Solution of Vibration Analysis on Fixed-Free Single-Walled Carbon Nanotube-Based Mass Sensor
![]()
Department of Mechanical Engineering, Kun-Shan University, Tainan, Chinese Taipei.
Email: hortl@mail.ksu.edu.tw
Received September 12th, 2011; revised October 13th, 2011; accepted October 25th, 2011
Keywords: Mass Sensor; Single-Walled Carbon Nanotube (SWCNT); Flexural Vibration Problem; Resonant Frequency Shift; Mass Sensor Mode Analysis
ABSTRACT
Fixed-free single-walled carbon nanotubes (SWCNTs) have attracted a lot of interest in recent years due to their suitability for a wide range of applications, such as field emission and vacuum microelectronic devices, nanosensors, and nanoactuators. Based on a cantilever beam-bending model with a rigid mass at the free end and mode analysis, an analytical solution is developed in the present study to deal with the resonant frequency and mode shapes of a SWCNTbased mass sensor. The resonant frequency shift and mode shape of the fixed-free SWCNTs caused by the addition of a nanoscale particle to the beam tip are examined in order to explore the suitability of SWCNTs as a mass detector device. The simulation results reveal that the volume of the added particle has little effect on the first resonant frequency. In contrast, the second resonant frequency decreases with increasing the volume of the added particle. Furthermore, the resonant frequency shift of the first mode is very obvious for the amount of added mass, and the second resonant frequency decreases rapidly with increasing volume of added particle. Therefore, the first and second resonant frequencies can be used in the measurement of the mass of added particle and its volume, respectively.
1. Introduction
Since their discovery in 1991 by Ijima, carbon nanotubes (CNTs) have demonstrated potential for use in a diverse range of applications, such as nanobiological devices and nanomechanical systems. Due to their remarkable mechanical, physical, and chemical properties, carbon nanotubes may be used as fluid conveyers or potential reinforcements in nanocomposite materials [1-3]. Since experiments at the nanoscale are extremely difficult to conduct, theoretical modeling of the mechanical response of CNTs has been carried out [4,5]. CNTs have been utilized as nanoactuators [6] and as nanosensors [7]. CNTs are extremely thin tubes whose diameters are on the order of a few nanometers, but whose lengths may be thousands of times larger. The use of vertically aligned single-walled CNTs (SWCNTs) for field emission and vacuum microelectronic devices, and as nanosensors and nanoactuators, is being actively explored [8,9]. Furthermore, Chen et al. [10] studied the effects of the geometric structure and an electric field on the electronic and optical properties of quasi-zero-dimensional finite CNTs using the tight-binding model coupled with curvature effects. Hsu et al. [11] developed a model that analyzes the resonant frequency of chiral SWCNTs subjected to a thermal vibration using the Timoshenko beam model that includes the effect of rotary inertia and shear deformation.
Several studies have investigated the use of CNTs as a mass sensor [7,12,13]. Compared to piezoelectric sensors, nanotubes provide better precision [12]. Wu et al. [13] simulated the mechanical responses of individual CNTs treated as cylindrical beams or thin shells using the continuum mechanics method with commercial FEM software. However, these studies adopted either experimental or numerical approaches, which are inherently time consuming and expensive. Saether et al. [14] proposed a simple formula of the resonant frequency of the fixedfree beam that uses its spring constant, and found that a change in the mass of the CNT resonator is indicated by a shift in the resonant frequency. The sensitivity and spatial resolution of the device can be varied by changing the dimensions of the resonator. In previous studies [15, 16], the current authors obtained accurate analytical solutions of vibration responses of atomic force microscope (AFM) and nanoscale processing using the modal superposition method. In the present study, a fixed-free SWCNT-based mass sensor is simulated as a cantilever beam-bending model with a rigid mass at the free end.The continuum mechanics method is used to obtain analytical solutions of vibration analysis, including the resonant frequency and mode shapes. The results show that the volume of the added particle has little effect on the first resonant frequency. In contrast, the second resonant frequency decreases with increasing the volume of the added particle. Furthermore, the resonant frequency shift of the first mode is very obvious for the amount of added mass, and the second resonant frequency decreases rapidly with increasing volume of added particle. Therefore, the first and second resonant frequencies can be used in the measurement of attached mass of added mass and its volume, respectively.
2. Analysis
Resonant frequency shift-based mass sensors are explored using a tip mass in the form of a nanoscale particle, which is attached to fixed-free SWCNTs. Techniques that facilitate the development of smaller, faster, cheaper, and more sensitive mass sensor devices are required. Using a hierarchical modeling scheme, the equivalentcontinuum modeling technique [17,18] can be used to predict the bulk mechanical behavior of nanostructured materials, such as the beam shown in Figure 1. A previous study [12] presented a cantilever-type CNT-based mass sensor. The present study considers the case of a fixed-free SWCNT with a nanoscale particle attached to its tip, as shown in Figure 2. The operation of a cantilever-based mass sensor is based on the fact that mass added to the tip causes a measurable shift in the resonant frequency of the fixed-free beam.
 (a)
(a) (b)
(b)
Figure 1. Computation model of SWCNT: (a) discrete model and (b) continuum model.
 (a)
(a) (b)
(b)
Figure 2. Fixed-free SWCNT with nanoscale particle at its tip: (a) discrete model and (b) continuum model.
Recently, the continuum mechanics method has been pplied to analyze the dynamic responses of individual CNTs. Based on the Euler-Bernoulli beam model [19], it is well known that the equation of motion of a free-vibration rod in the limited to a small amplitude is governed by the fourth-order wave equation:
 (1)
(1)
where 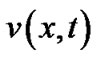 is the transversal displacement response,
is the transversal displacement response, 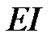 is the flexural stiffness, and
is the flexural stiffness, and 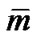 is the mass per unit length. The natural mechanical resonant frequency is induced in a cantilever carbon nanotube when the applied frequency approaches the resonant frequency. In this study, a SWCNT-based mass sensor is simulated as a cantilever beam with a rigid mass at the free end. The continuum mechanics method is used to obtain the resonant frequency and the mode shapes of a sensor analytically by mode analysis method. One form of solution of Equation (1) can be obtained easily by the separation of variables:
is the mass per unit length. The natural mechanical resonant frequency is induced in a cantilever carbon nanotube when the applied frequency approaches the resonant frequency. In this study, a SWCNT-based mass sensor is simulated as a cantilever beam with a rigid mass at the free end. The continuum mechanics method is used to obtain the resonant frequency and the mode shapes of a sensor analytically by mode analysis method. One form of solution of Equation (1) can be obtained easily by the separation of variables:
 (2)
(2)
where 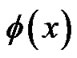 is a specific shape of the free-vibration motion with time-dependent amplitude
is a specific shape of the free-vibration motion with time-dependent amplitude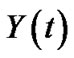 .
. 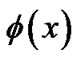 can be expressed as:
can be expressed as:
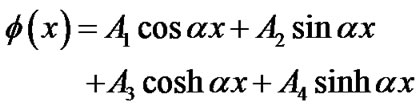 (3)
(3)
where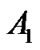 ,
, 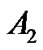 ,
, 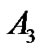 , and
, and 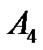 are real constants that can be determined using the boundary condition.
are real constants that can be determined using the boundary condition.
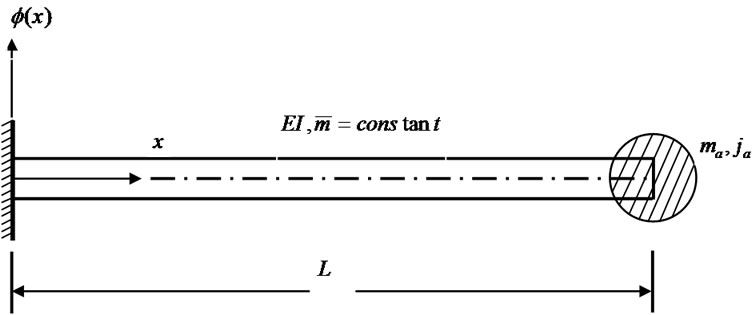
Consider the cantilever beam with a rigid mass at the free end shown in Figure 2 to which a rigid lumped mass 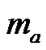 with a rotary moment of inertia
with a rotary moment of inertia 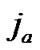 is attached. The moment and shear are no longer equal to zero at the other end due to the presence of the lumped mass. These internal force components are shown on the free-body diagram in Figure 3 along with the translational and rotary inertial force components
is attached. The moment and shear are no longer equal to zero at the other end due to the presence of the lumped mass. These internal force components are shown on the free-body diagram in Figure 3 along with the translational and rotary inertial force components 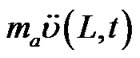 and
and , respectively. Under free-vibration conditions with resonant frequency
, respectively. Under free-vibration conditions with resonant frequency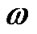 , acceleration
, acceleration 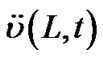 and its derivative are:
and its derivative are:
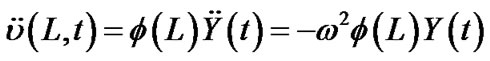 (4)
(4)
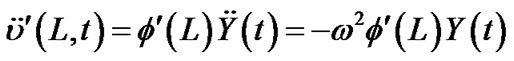 (5)
(5)
where  is the resonant frequency of the SWCNT. Moreover, force and moment equilibrium of the rigid mass requires that the following four boundary conditions be satisfied:
is the resonant frequency of the SWCNT. Moreover, force and moment equilibrium of the rigid mass requires that the following four boundary conditions be satisfied:
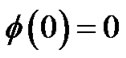 (6)
(6)
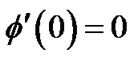 (7)
(7)
 (a)
(a)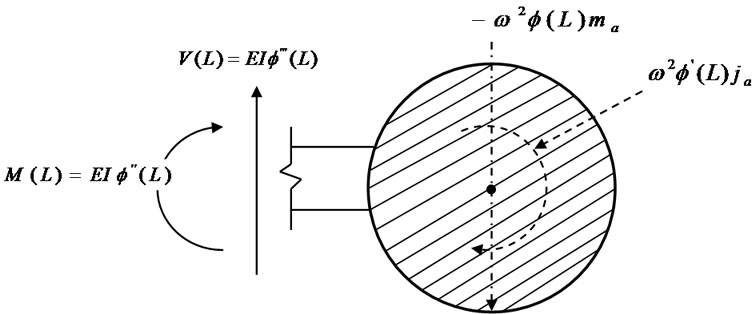 (b)
(b)
Figure 3. Fixed-free SWCNT with nanoscale particle at its tip: (a) SWCNT properties; (b) Forces acting on the nanoscale particle.
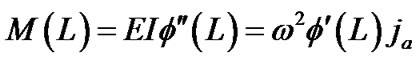 (8)
(8)
 (9)
(9)
Substituting Equation (3) and its derivative expressions into these equations gives
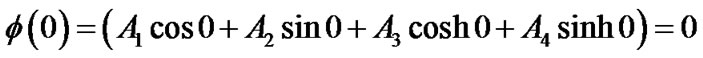 (10)
(10)
 (11)
(11)
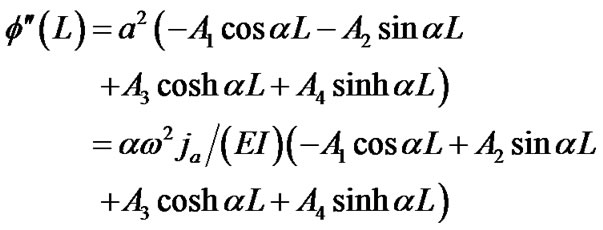 (12)
(12)
 (13)
(13)
Making use of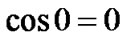 ,
, 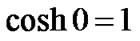 ,
,  , and
, and , Equations (10) and (11) yield
, Equations (10) and (11) yield 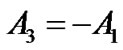 and
and . Substituting these equalities into Equations (12) and (13), changing all signs, and placing the resulting expressions in matrix form, one obtains: (see (14))where
. Substituting these equalities into Equations (12) and (13), changing all signs, and placing the resulting expressions in matrix form, one obtains: (see (14))where 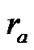 and
and 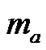 are the radius and the added mass of the particle, respectively.
are the radius and the added mass of the particle, respectively. 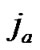 and
and 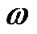 can be defined as followed:
can be defined as followed:
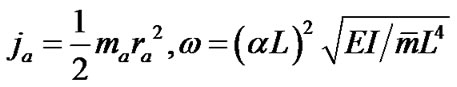 (15)
(15)
For coefficients 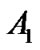 and
and 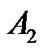 to be nonzero, the determinant of the square matrix in this equation must equal zero, thus giving the frequency equation:
to be nonzero, the determinant of the square matrix in this equation must equal zero, thus giving the frequency equation:
 (16)
(16)
The solution of this transcendental equation provides the values of , which represent the frequencies of vibration of the cantilever beam with a rigid mass at the free end. Either form of Equation (14) can now be employed to express coefficient
, which represent the frequencies of vibration of the cantilever beam with a rigid mass at the free end. Either form of Equation (14) can now be employed to express coefficient 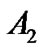 in terms of
in terms of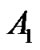 ; the first gives:
; the first gives:
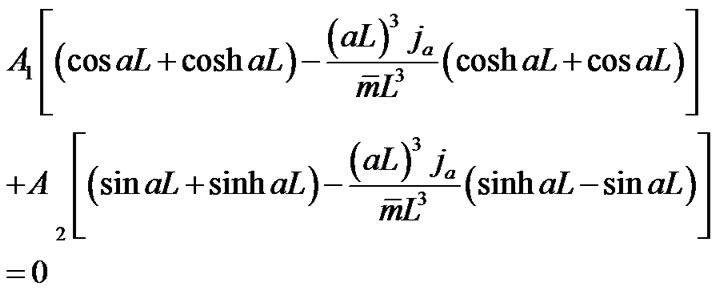 (17)
(17)
or
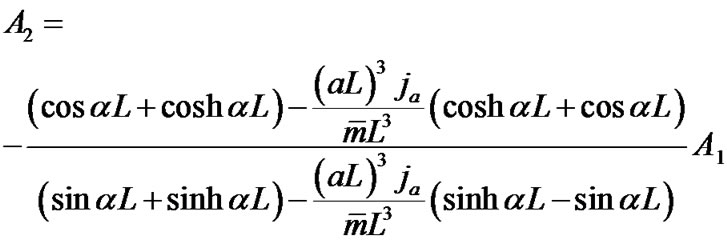 (18)
(18)
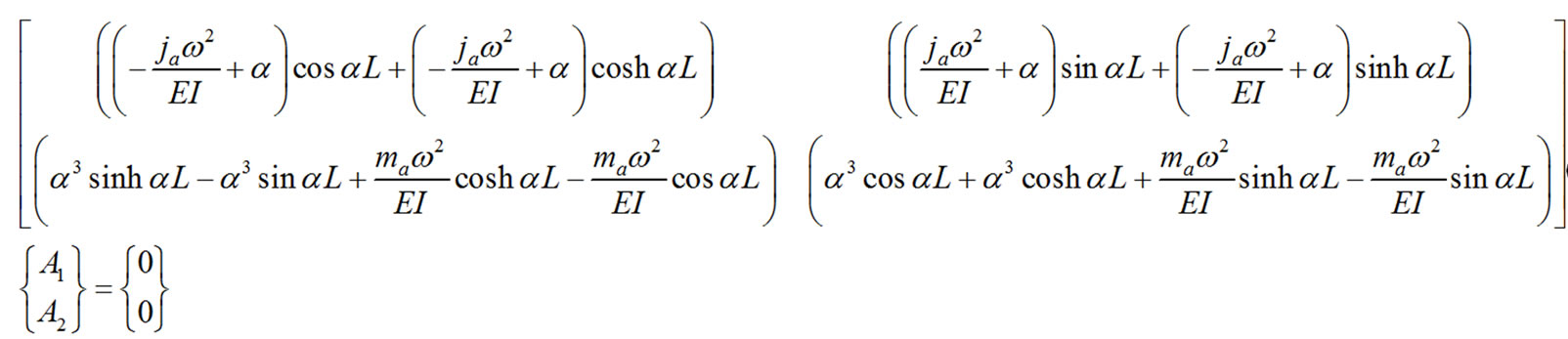 (14)
(14)
This result along with the previously obtained conditions that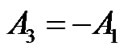 and
and 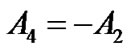 allows the mode-shape expression of Equation (3) to be written in the form of Equation (19).
allows the mode-shape expression of Equation (3) to be written in the form of Equation (19).
Substituting separately the frequency-equation roots for  into this expression, one obtains the corresponding mode-shape functions.
into this expression, one obtains the corresponding mode-shape functions.
3. Results and Discussion
In this study, a tip mass in the form of a nanoscale particle is attached to a fixed-free SWCNT, whose behavior of the nanotube is investigated using mass sensor mode analysis. A resonant frequency shift-based mass sensor is made using the fixed-free SWCNT. The dimensions of the SWCNT are as follows: inner radius 9.9 nm, outer radius 16nm, stiffness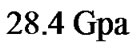 , mass per unit length
, mass per unit length 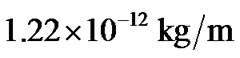 and length 6.8 μm. In order to investigate the effects of attached mass on the resonant frequency,
and length 6.8 μm. In order to investigate the effects of attached mass on the resonant frequency, 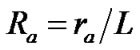 and
and 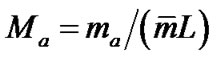 were set as the dimensionless values of radius and added mass, respectively.
were set as the dimensionless values of radius and added mass, respectively.
Figure 4 and Figure 5 show the variation in the first and second resonant frequencies for fixed-free SWCNT with various added mass for various radii, respectively. The simulation results in the two figures indicate that the first and second resonant frequencies decrease with increasing attached mass. Furthermore, for a constant attached mass, Figure 4 reveals that the volume of added mass has little effect on the first resonant frequency. In contrast, Figure 5 shows that the second resonant frequency decreases with increasing the volume of added mass.
Figure 6 and Figure 7 show the variation in the first and second resonant frequencies for a fixed-free SWCNT for various radii and added mass of the particle. The two figures show that added mass significantly affects the first and second resonant frequencies, especially the former. Thus, the first resonant frequency can be used in the measurement of attached mass, Figure 7 shows that the second resonant frequency decreases rapidly with increasing radius of added mass. This is due to the rotating effect having a larger effect on the second resonant frequency. Therefore, the second resonant frequency can be
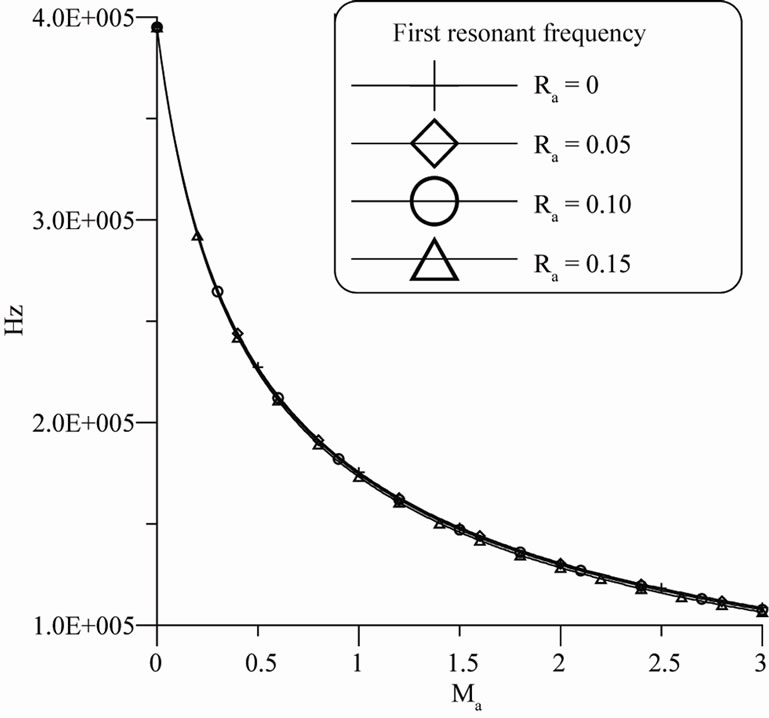
Figure 4. Variation in the first resonant frequency for a fixed-free SWCNT with various added mass for various radii of the particle.
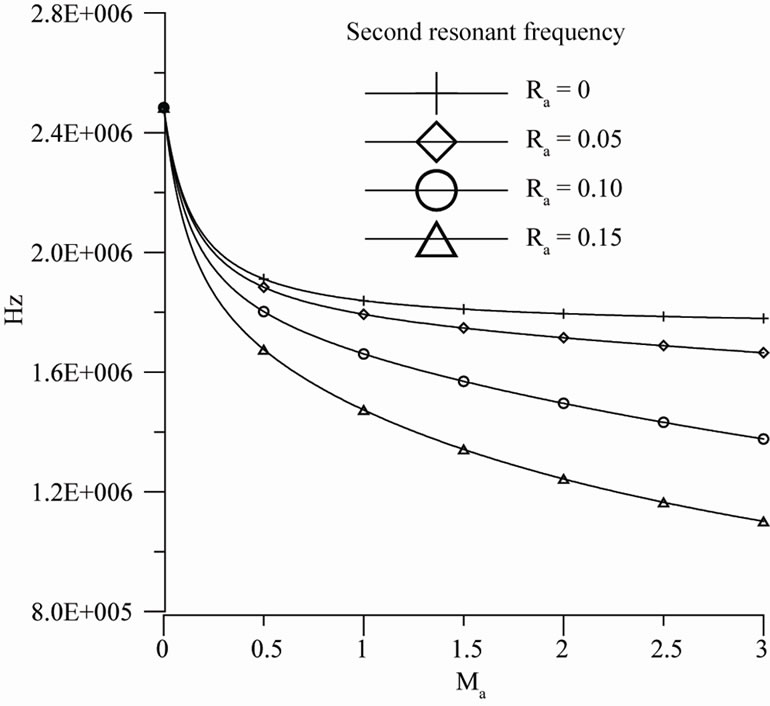
Figure 5. Variation in the second resonant frequency for a fixed-free SWCNT with various added mass for various radii of the particle.
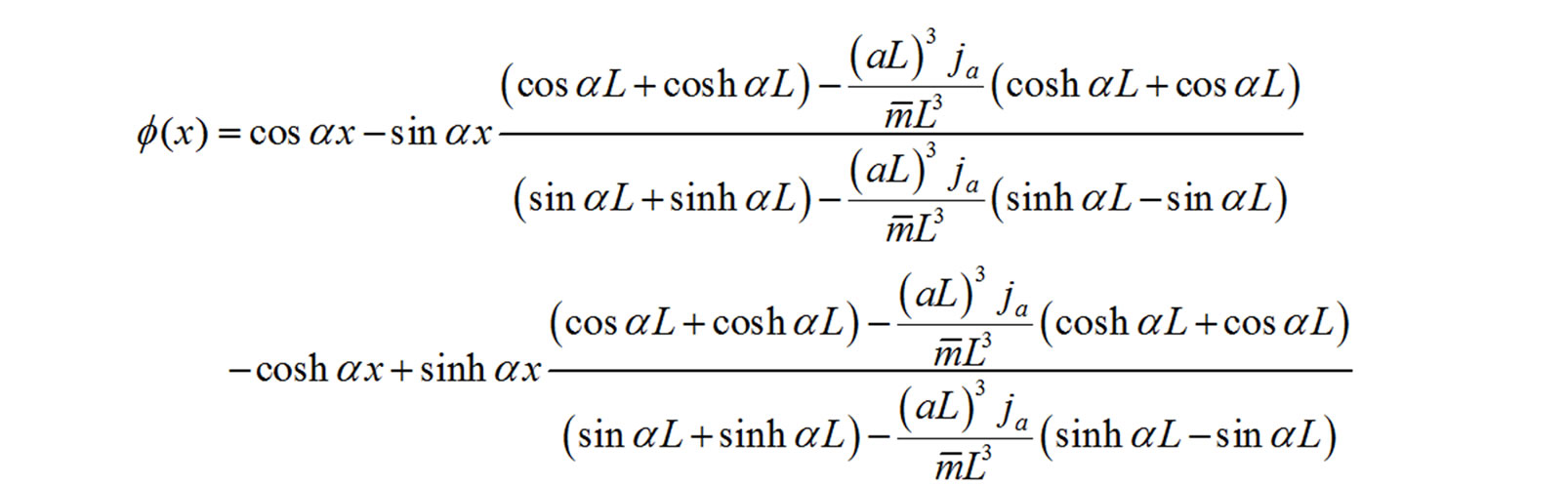 (19)
(19)

Figure 6. Variation in the first resonant frequency for a fixed-free SWCNT with various radii of the particle for various added mass.
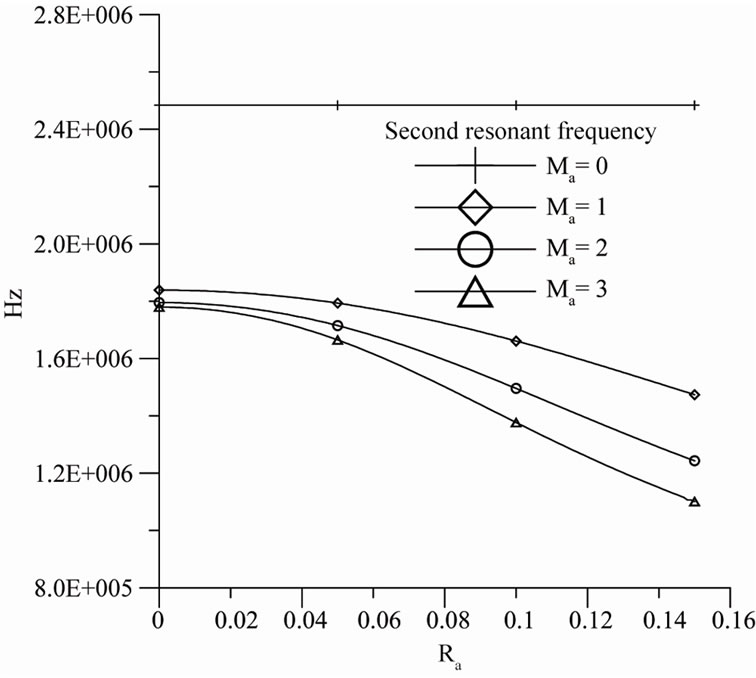
Figure 7. Variation in the second resonant frequency for a fixed-free SWCNT with various radii of the particle for various added mass.
used in the measurement of the radius of added mass.
4. Conclusion
The mass sensor mode analysis method was applied to an SWCNT-based mass sensor to determine the mass and volume of an attached nanoparticle. The first and second resonant frequencies decrease with increasing attached mass. It was found that the resonant frequency shift of the first mode is not obvious when the volume of the particle is changed. However, the volume of the added nanoparticle significantly affects the second resonant frequency. Moreover, the resonant frequency shift of first mode is very obvious when the attached mass is changed; it is thus suggested that the first resonant frequency be used in the measurement of attached mass. Furthermore, the second resonant frequency decreases rapidly with increasing volume of additional mass; the measurement of the volume of added mass can be conducted using the second resonant frequency. SWCNTs can thus be used as resonant frequency shift-based mass sensors.
5. Acknowledgements
The authors would like to thank the National Science Council of Taiwan Republic of China, for providing financial support under grant NSC 99-2221-E-168-021.
REFERENCES
- A. Bianco, K. Kostarelos and M. Prato, “Applications of Carbon Nanotubes in Drug Delivery,” Current Opinion in Chemical Biology, Vol. 9, No. 6, 2005, pp. 674-679. doi:10.1016/j.cbpa.2005.10.005
- R. S. Ruoff and D. C. Lorents, “Mechanical and Thermal Properties of Carbon Nanotubes,” Carbon, Vol. 33, No. 7, 1995, pp. 925-930. doi:10.1016/0008-6223(95)00021-5
- D. Srivastava, M. Menon and K. Cho, “Computational Nanotechnology with Carbon Nanotubes and Fullerenes,” Computing in Science and Engineering, Vol. 3, No. 4, 2001, pp. 42-55. doi:10.1109/5992.931903
- R. Saito, G. Dresselhaus and M. S. Dresselhaus, “Physical Properties of Carbon Nanotubes,” Imperial College, London, 1998. doi:10.1142/9781860943799
- P. J. F. Harris, “Carbon Nanotubes and Related Structures,” Cambridge University Press, Cambridge, 1999. doi:10.1017/CBO9780511605819
- H. Dai, J. H. Hafner, A. G. Rinzler, D. T. Colbert and R. E. Smalley, “Nanotubes as Nanoprobes in Scanning Probe Microscopy,” Letters to Nature, Vol. 384, 1996, pp. 147-150. doi:10.1038/384147a0
- P. Poncharal, Z. L. Wang, D. Ugarte and W. A. D. Heer, “Electrostatic Deflections and Electro-Mechanical Resonances of Carbon Nanotubes,” Science, Vol. 283, No. 5407, 1999, pp. 1513-1516. doi:10.1126/science.283.5407.1513
- H. J. Qi, K. B. K. Teo, K. K. S. Lau, M. C. Boyce, W. I. Milne, J. Roberson and K. K. Gleason, “Determination of Mechanical Properties of Carbon Nanotubes and Vertically Aligned Carbon Nanotube Forests Using Nanoindentation,” Journal of the Mechanics and Physics of Solids, Vol. 51, No. 11-12, 2003, pp. 2213-2237. doi:10.1016/j.jmps.2003.09.015
- G. W. Wang, Y. P. Zhao and G. T. Yang, “The Stability of a Vertical Single-Walled Carbon Nanotube under Its Own Weight,” Materials & Design, Vol. 25, No. 6, 2004, pp. 453-457. doi:10.1016/j.matdes.2004.01.003
- R. B. Chen, C. H. Lee, C. P. Chang and M. F. Lin, “Electronic and Optical Properties of Finite Carbon Nanotubes in an Electric Field,” Nanotechnology, Vol. 18, No. 7, 2007, Article ID 075704. doi:10.1088/0957-4484/18/7/075704
- J. C. Hsu, R. P. Chang and W. J. Chang, “Resonance Frequency of Chiral Single-Walled Carbon Nanotubes Using Timoshenko Beam Theory,” Physics Letters A, Vol. 372, No. 16, 2008, pp. 2757-2759. doi:10.1016/j.physleta.2008.01.007
- R. Mateiu, Z. J. Davis, D. N. Madsen, K. Mølhave, P. Bøggild, A. M. Rassmusen, M. Brorson, C. J. H. Jacobsen and A. Boisen, “An Approach to a Multi-Walled Carbon Nanotube-Based Mass Sensor,” Microelectronic Engineering, Vol. 73-74, 2004, pp. 670-674. doi:10.1016/S0167-9317(04)00181-9
- D. H. Wu, W. T. Chien, C. S. Chen and H. H. Chen, “Resonant Frequency Analysis of Fixed-Free SingleWalled Carbon Nanotube-Based Mass Sensor,” Sensors and Actuators A: Physical, Vol. 126, No. 1, 2006, pp. 117-121. doi:10.1016/j.sna.2005.10.005
- E. Saether, S. J. V. Frankland and R. B. Pipes, “Transverse Mechanical Properties of Single-Walled Carbon Nanotube Crystals. Part I. Determination of Elastic Moduli,” Composites Science and Technology, Vol. 63, No. 11, 2003, pp. 1543-1550. doi:10.1016/S0266-3538(03)00056-3
- T.-L. Horng, “Analytical Solution of Flexural Vibration Responses on Nanoscale Processing Using Atomic Force Microscopy,” Journal of Materials Processing Technology, Vol. 209, No. 6, 2009, pp. 2940-2945. doi:10.1016/j.jmatprotec.2008.06.059
- T.-L. Horng, “Analyses of Vibration Responses on Nanoscale Processing in a Liquid Using Tapping-Mode Atomic Force Microscopy,” Applied Surface Science, Vol. 256, No. 1, 2009, pp. 311-317. doi:10.1016/j.apsusc.2009.08.021
- K. Sohlberg, B. G. Sumpter, R. E. Tuzun and D. W. Noid, “Continuum Methods of Mechanics as a Simplified Approach to Structural Engineering of Nanostructures,” Nanotechnology, Vol. 9, No. 1, 1998, pp. 30-36. doi:10.1088/0957-4484/9/1/004
- Y. J. Liu and X. L. Chen, “Continuum Models of Carbon Nanotube-Based Composites Using the Boundary Element Method,” Electronic Journal of Boundary Elements, Vol. 1, No. 2, 2003, pp. 316-335.
- S. P. Timoshenko and J. M. Gere, “Theory of Elastic Stability,” McGraw-Hill, New York, 1961.

