American Journal of Computational Mathematics
Vol.06 No.02(2016), Article ID:67729,12 pages
10.4236/ajcm.2016.62015
Approximate Solutions for a Class of Fractional-Order Model of HIV Infection via Linear Programming Problem
Samaneh Soradi Zeid1, Mostafa Yousefi2, Ali Vahidian Kamyad3
1Department of Mathematics, Faculty of Mathematics, University of Sistan and Baluchestan, Zahedan, Iran
2National Iranian Oil Products Distribution Company (NIOPDC), Zahedan Region, Zahedan, Iran
3Department of Mathematics, Ferdowsi University of Mashhad, Mashhad, Iran

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 May 2016; accepted 24 June 2016; published 27 June 2016
ABSTRACT
In this paper, we provide a new approach to solve approximately a system of fractional differential equations (FDEs). We extend this approach for approximately solving a fractional-order differential equation model of HIV infection of CD4+T cells with therapy effect. The fractional derivative in our approach is in the sense of Riemann-Liouville. To solve the problem, we reduce the system of FDE to a discrete optimization problem. By obtaining the optimal solutions of new problem by minimization the total errors, we obtain the approximate solution of the original problem. The numerical solutions obtained from the proposed approach indicate that our approximation is easy to implement and accurate when it is applied to a systems of FDEs.
Keywords:
Riemann-Liouville Derivative, Fractional HIV Model, Optimization Linear Programming, Discritezation

1. Introduction
In recent years, scientists have been interested in studying the fractional calculus and the FDEs in different fields of engineering, physics, mathematics, biology, finance, biomechanics and electrochemical processes (see [1] - [8] , for more details). Also, it has been shown that modelling the behavior of many biological systems that governed by FDEs has more advantages than classical integer-order modelling [9] . Readers interested in FDEs are referred to [10] - [17] . Although great efforts have been made to find numerical and analytical techniques for solving FDE, for example, predictor-corrector method [18] , the Adomian decomposition [19] , the variational iteration method [20] , collocation using spline functions [21] and matrix expression given by [22] [23] , but most of these FDEs do not have analytic solutions.
In this paper, at first, we approximate the fractional derivative by a finite difference method and then use the AVK approach [24] to obtain a new approximate solution for the FDEs. This approach substitutes the FDEs with an equivalent minimization problem in which the optimal solution of this problem is the approximate solution of the original FDE. Moreover, since the error of this approach is minimized, the approximate solutions are the best solutions for the original problem. We employ this approximation to get numerical solution of a system of FDEs which has been used for modelling HIV infection of CD4+T cells.
The discussion of paper will be as follows: in the next section, we express the fractional HIV model and introduce the notations that used in the rest of this paper. In Section 3, we design an efficient approach to approximate the fractional derivative and use it in our numerical method for solving FDEs. Some numerical examples are displayed in Section 4. Finally, conclusions are included in the last section.
2. The Problem
Consider the following fractional-order differential equation model of HIV infection of CD4+T cells [25] :
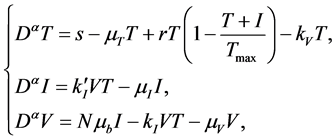 (1)
(1)
with the initial conditions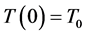 ,
, 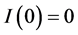 and
and , in which the parameter values reported by Table 1.
, in which the parameter values reported by Table 1.
Following Theorem 1 of [25] , we note that (1) along with its initial conditions possesses a unique solution which is non-negative. Throughout this paper, we set  (
(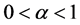 ) as the Riemann-Liouville derivative of order
) as the Riemann-Liouville derivative of order  defined by [26] :
defined by [26] :
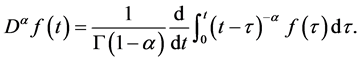 (2)
(2)
The aim of this paper is to extend the application of the AVK approach to solve a fractional order model for this HIV infection model of CD4+T cells. So, in the next section, at first we convert the original FDE to an
Table 1. Variables and parameters for HIV infection model.
optimization problem based on minimization of error. By discretizing the new problem and approximating the Riemann-Liouville fractional derivative by a finite difference method, we obtaine the best approximate solution of the original FDE.
3. AVK Approach for Solving Approximately FDEs
Consider a general system of FDEs as follows:
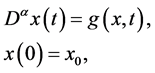 (3)
(3)
where 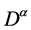 (
( ) is the Riemann-Liouville derivative of order
) is the Riemann-Liouville derivative of order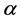 , g is an riemann integrable time varying function,
, g is an riemann integrable time varying function,  ,
, 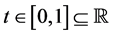 and A is a compact subset in
and A is a compact subset in

Definition 1. For problem (3) we define the following functional 

where 




Here, we convert the problem (4) to a nonlinear programming (NLP) as follow:

Now, to reach the approximating solution for the original problem (3) it is sufficient to solve the minimization problem (6). Hence, we need the following mean theorem [27] and corollary.
Theorem 1. Let h be a nonnegative continuous function on



Corollary 1. Necessary and sufficient condition for the trajectory 
To develop the numerical solution of problem (6) approximately, we defined the grid size in time by
for some positive integer m, so the grid points in the time interval 


By the above notations, problem (6) is now approximated by the following optimization problem:

By using the ending point in any subinterval for approximating integrals, problem (7) is now approximated by the following optimization problem:

Now, we approximate fractional derivative 

Define

In order to better illustrate the numerical approach, we also introduce the following difference operator:

Then,

Hence 
suppose



Thus, we simply get problem (8) in the following form:

in which, 

We solved this optimization problem by linear programming (LP) formulation which is done in what follows.
Lemma 1. Let pairs

where I is a compact set. Then

Proof. Since, 















So
Now, by lemma 1, problem (14) can be converted to the following equivalent LP problem:

By obtaining the solution of this problem, we recognize the value of unknown admissible


4. Numerical Examples
In this section, we give some numerical examples and apply the method presented in the last sections for solving them. Moreover, we extend this approach for approximately solving a model of HIV infection of CD4+T cells with therapy effect including a system of FDEs. These test problems demonstrate the validity and efficiency of this approximation.
Example 1. As first example, we compute


derivatives are derived from
Figure 1 shows the results by using approximation (10)-(13) for 
Now, assume that




In this example, the maximum absolute errors computed by Equation (16) for 
Example 2. Consider the following initial value problem:

with initial condition
We know that


Figure 1. Analytic solution and numerical approximation (10), with various choices of m and
Table 2. Maximum absolute error for Example 1.
In the case of
From numerical results we can indicate that the solution of FDE approaches to the solution of integer order differential equation, whenever 
Example 3. Consider the following FDE:

where 

The exact solution of this equation is

Table 4 shows the exact solution and the approximate solution for equation (18) by solving problem (15) for 

Example 4. Now we want to solve the fractional-order differential equation model of HIV infection of CD4+T cells (1) For the parameter values given in Table 1. The system (1) can be expressed in a vector form as follows:
Figure 2. Exact and approximation solutions for problem in Example 2 with 
Figure 3. Exact and approximation solutions for problem in Example 2 with 

where 

For numerical simulations we assumed 350 days for treatment period. With the change of variables
Figure 4. Exact and approximation solutions for problem in Example 2 with 
Table 3. Maximum absolute error for different values of 
Table 4. Numerical values with 

Figure 5. Analytic solution and numerical approximation (15) for Example 3 for
Figure 6. Analytic solution and numerical approximation (15) for Example 3 for
we converted period 


Table 5. Maximum absolute error for 

with the initial condition (20). To solve this optimization problem, by approximating integrals as before, we transformed (21) to a discretized problem in the following form:

In problem (21) and (22), the factor 350 is omitted because of having no effect on the solution of it. Then, the minimum problem (22) converted to a linear programming problem with the following change of variables:

Now, we approximate fractional derivatives from (10)-(13). Our approach introduces an approximate solution for the fractional HIV model based on minimization the total error. The maximum absolute errors (16) with m = 100 and different values of 
5. Conclusions
In this paper, the finite difference method discrete time AVK approach has been successfully used for finding the solutions of a system of FDEs such as a model for HIV infection of CD4+T cells. Our approach introduces an approximate solution for the FDEs based on the minimization of the total error. In the suggested method, the original problem reduces to an optimization problem. By discretizing the new problem and solving it, we obtain the best approximate solution of the original problem. Results represent a unifying approach for numerical approximation of differential equations of fractional order. Since this method is not based on point to point error, but according to its results, it is clear that there is no difference between the exact and approximate solutions in point to point case.
Three numerical examples are given and the results are compared with the exact solutions and with the other methods. It is shown that, as the order of fractional derivatives approaches to 1, the numerical solutions for the FDEs approach the clasicall solutions of the problem. Then we use this technique for finding approximate solutions of FDEs system of a model for HIV infection of CD4+T cells. The result demonstrates the validity of the approach.
Cite this paper
Samaneh Soradi Zeid,Mostafa Yousefi,Ali Vahidian Kamyad, (2016) Approximate Solutions for a Class of Fractional-Order Model of HIV Infection via Linear Programming Problem. American Journal of Computational Mathematics,06,141-152. doi: 10.4236/ajcm.2016.62015
References
- 1. Barkai, E., Metzler, R. and Klafter, J. (2000) From Continuous Time Random Walks to the Fractional Fokker-Planck Equation. Physical Review E, 61, 132.
http://dx.doi.org/10.1103/PhysRevE.61.132 - 2. Bhrawy, A.H., Doha, E.H., Tenreiro Machado, J.A. and Ezz-Eldien, S.S. (2015) An Efficient Numerical Scheme for Solving Multi-Dimensional Fractional Optimal Control Problems with a Quadratic Performance Index. Asian Journal of Control, 17, 2389-2402.
http://dx.doi.org/10.1002/asjc.1109 - 3. Podlubny, I. (1998) Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Vol. 198, Academic Press, Mathematics in Science and Engineering, 366.
- 4. Magin, R.L. (2006) Fractional Calculus in Bioengineering. Vol. 149, Begell House Publishers, Redding.
- 5. Raberto, M., Scalas, E. and Mainardi, F. (2002) Waiting-Times and Returns in High-Frequency Financial Data: An Empirical Study. Physica A: Statistical Mechanics and its Applications, 314, 749-755.
- 6. Tricaud, C. and Chen, Y.Q. (2010) An Approximate Method for Numerically Solving Fractional Order Optimal Control Problems of General Form. Computers & Mathematics with Applications, 59, 1644-1655.
http://dx.doi.org/10.1016/j.camwa.2009.08.006 - 7. Zamani, M., Karimi, G. and Sadati, N. (2007) Fopid Controller Design for Robust Performance Using Particle Swarm Optimization. Fractional Calculus and Applied Analysis, 10, 169-188.
- 8. Bagley, R.L. and Torvik, P.J. (1983) A Theoretical Basis for the Application of Fractional Calculus to Viscoelasticity. Journal of Rheology, 27, 201-210.
http://dx.doi.org/10.1122/1.549724 - 9. Anastasio, T.J. (1994) The Fractional-Order Dynamics of Bainstem Vestibulo-Oculomotor Neurons. Biological Cybernetics, 72, 69-79.
http://dx.doi.org/10.1007/BF00206239 - 10. Liu, F., Anh, V. and Turner, I. (2004) Numerical Solution of the Space Fractional Fokker-Planck Equation. Journal of Computational and Applied Mathematics, 166, 209-219.
http://dx.doi.org/10.1016/j.cam.2003.09.028 - 11. Shen, S., Liu, F., Anh, V. and Turner, I. (2008) The Fundamental Solution and Numerical Solution of the Riesz Fractional Advection-Dispersion Equation. IMA Journal of Applied Mathematics, 73, 850-872.
http://dx.doi.org/10.1093/imamat/hxn033 - 12. Bhrawy, A.H., Baleanu, D. and Assas, L.M. (2013) Efficient Generalized Laguerre-Spectral Methods for Solving Multi-Term Fractional Differential Equations on the Half Line. Journal of Vibration and Control, 20, 973-985.
- 13. Pooseh, S., Almeida, R. and Torres, D. (2013) Numerical Approximations of Fractional Derivatives with Applications. Asian Journal of Control, 15.3, 698-712.
http://dx.doi.org/10.1002/asjc.617 - 14. Grahovac, N.M. and Spasic, D.T. (2013) Multivalued Fractional Differential Equations as a Model for an Impact of Two Bodies. Journal of Vibration and Control, 20, 1017-1032.
- 15. Saadatmandi, A. and Dehghan, M. (2011) A Legendre Collocation Method for Fractional Integro-Differential Equations. Journal of Vibration and Control, 17, 2050-2058.
http://dx.doi.org/10.1177/1077546310395977 - 16. Kayedi-Bardeh, A., Eslahchi, M.R. and Dehghan, M. (2014) A Method for Obtaining the Operational Matrix of Fractional Jacobi Functions and Applications. Journal of Vibration and Control, 20, 736-748.
http://dx.doi.org/10.1177/1077546312467049 - 17. Dhabale, A.S., Dive, R., Aware, M.V. and Das, S. (2015) A New Method for Getting Rational Approximation for Fractional Order Differ Integrals. Asian Journal of Control, 17, 2143-2152.
- 18. Zhao, L. and Deng, W. (2014) Jacobian-Predictor-Corrector Approach for Fractional Differential Equations. Advances in Computational Mathematics, 40, 137-165.
http://dx.doi.org/10.1007/s10444-013-9302-7 - 19. Momani, S. and Odibat, Z. (2006) Analytical Solution of a Time-Fractional Navier-Stokes Equation by Adomian Decomposition Method. Applied Mathematics and Computation, 177, 488-494.
http://dx.doi.org/10.1016/j.amc.2005.11.025 - 20. Odibat, Z.M. and Momani, S. (2006) Application of Variational Iteration Method to Nonlinear Differential Equations of Fractional Order. International Journal of Nonlinear Sciences and Numerical Simulation, 7, 27-34.
http://dx.doi.org/10.1515/IJNSNS.2006.7.1.27 - 21. Blank, L. (1996) Numerical Treatment of Differential Equations of Fractional Order. Department of Mathematics, University of Manchester.
- 22. Podlubny, I. (2000) Matrix Approach to Discrete Fractional Calculus. Fractional Calculus and Applied Analysis, 3, 359-386.
- 23. Podlubny, I., Chechkin, A., Skovranek, T., Chen, Y. and Jara, B.M.V. (2009) Matrix Approach to Discrete Fractional Calculus II: Partial Fractional Differential Equations. Journal of Computational Physics, 228, 3137-3153.
http://dx.doi.org/10.1016/j.jcp.2009.01.014 - 24. Badakhshan, K.P. and Kamyad, A.V. (2007) Using AVK Method to Solve Nonlinear Problems with Uncertain Parameters. Applied Mathematics and Computation, 189, 27-34.
http://dx.doi.org/10.1016/j.amc.2006.11.172 - 25. Ding, Y. and Ye, H. (2009) A Fractional-Order Differential Equation Model of HIV Infection of CD4+T-Cells. Mathematical and Computer Modelling, 50, 386-392.
http://dx.doi.org/10.1016/j.mcm.2009.04.019 - 26. Podlubny, I. (1999) Fractional Differential Equations. Academic Press, San Diego.
- 27. Badakhshan, K.P. and Kamyad, A.V. (2007) Numerical Solution of Nonlinear Optimal Control Problems Using Nonlinear Programming. Applied Mathematics and Computation, 187, 1511-1519.
http://dx.doi.org/10.1016/j.amc.2006.09.074 - 28. Zeid, S.S. and Kamyad, A.V. (2014) On Generalized High Order Derivatives of Nonsmooth Functions. American Journal of Computational Mathematics, 4, 317-328.
http://dx.doi.org/10.4236/ajcm.2014.44028 - 29. Odibat, Z. and Momani, S. (2008) An Algorithm for the Numerical Solution of Differential Equations of Fractional Order. Journal of Applied Mathematics & Informatics, 26, 15-27.














