American Journal of Computational Mathematics
Vol.05 No.03(2015), Article ID:59430,12 pages
10.4236/ajcm.2015.53028
Peristaltic Pumping of a Conducting Sisko Fluid through Porous Medium with Heat and Mass Transfer
Nabit Tawfiq Mohamed El-Dabe, Ahmed Younis Ghaly, Sallam Nagy Sallam, Khaled Elagamy, Yasmeen Mohamed Younis
Department of Mathematics, Faculty of Education, Ain Shams University, Cairo, Egypt
Email: mastermath2003@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 July 2015; accepted 4 September 2015; published 7 September 2015
ABSTRACT
The mathematical model is presented for the flow of peristaltic pumping of a conducting non- Newtonian fluid obeying Sisko model through a porous medium under the effect of magnetic field with heat and mass transfer. The solutions of the system of equations which represent this motion are obtained analytically using perturbation technique after considering the approximation of long wave length. The formula of the velocity with temperature and concentration of the fluid is obtained as a function of the physical parameters of the problem. The effects of these parameters on these solutions are discussed numerically and illustrated graphically through some graphs.
Keywords:
Peristaltic, Sisko Fluid, MHD, Heat and Mass Transfer, Chemical Reaction

1. Introduction
Peristalsis is a form of fluid transport induced by a progressive wave of area contraction or expansion along the walls of distensible duct containing a liquid or mixture. A peristaltic pump is a device for pumping fluids, generally from a region of lower to higher pressure, by means of a contraction wave traveling along a tube like structure. Shapiro et al. [1] explained the basic principles and brought out clearly the significances of the various parameters governing the flow. The non-Newtonian effects in peristaltic motion were included in Kaimal [2] . Later several mathematical and experimental models have been developed to understand the fluid mechanical aspects of peristaltic motion. A large body of work already exists on mathematical and experimental models containing a Newtonian or non-Newtonian fluid in a channel.
Peristalsis also have industrial and biological applications like sanitary fluid transport blood pumps in heart lungs machines and peristaltic transport of toxic liquid is used in nuclear industries. Some recent investigations made to discuss the mechanism of peristalsis include the works. Radhakrishnamacharya and Srinivasulu [3] studied the influence of wall properties on peristaltic transport with heat transfer. Mekheimer and Abd Elmaboud [4] analyzed the influence of heat transfer and magnetic field on peristaltic transport of Newtonian fluid in a vertical annulus. Hayat et al. [5] studied the effect of heat transfer on the peristaltic flow of an electrically conducting fluid in a porous space. Krishna Kumari et al. [6] studied the peristaltic pumping of a magnetohydrodynamic Casson fluid in an inclined channel. Ravi Kumar et al. [7] considered power-law fluid in the study of peristaltic transport.
The effect of porous medium on the motion of the fluid has been studied by many authors. Elshehawey et al. [8] studied the effect of porous medium on peristaltic motion of a Newtonian fluid. Eldabe [9] studied magnetohydrodynamic flow through a porous medium fluid at a rear stagnation point. Eldabe et al. [8] studied MHD flow and heat transfer in a viscoelastic incompressible fluid confined between a horizontal stretching sheet and a parallel porous wall. Elshehawey et al. [9] studied the peristaltic motion of a Generalized Newtonian fluid through a porous medium. El-Dabe et al. [10] studied the magnetohydrodynamic flow and heat transfer for a peristaltic motion of Carreau fluid through a porous medium.
The study of the influence of mass and heat transfer on Newtonian and non-Newtonian fluids has become important in the last few years. This importance is due to a number of industrial processes. Examples are food-processing, biochemical operations and transport in polymers. Eldabe et al. [11] studied the heat and mass transfer in hydromagnetic flow of the non-Newtonian fluid with heat source over an accelerating surface through a porous medium. Srinivas and Kothandapani [12] dealt with peristalsis and heat transfer. Hayat et al. [13] - [15] analyzed the peristaltic mechanism with heat transfer. Eldabe et al. [16] studied the effect of couple stresses on the MHD of a non-Newtonian unsteady flow between two parallel porous plates. The main aim of this study is to investigate the problem of the peristaltic flow of a conducting Sisko fluid in a porous channel with heat and mass transfer; the system of non-linear partial differential equations which describe this motion with heat and mass transfer subjected to the appropriate boundary conditions is solved analytically by using perturbation method. The expressions of the velocity, the temperature and the concentration are determined. The effects of different parameters on these expressions are discussed through graphs.
2. Basic Equations
The basic equations governing the flow of an incompressible fluid are expressed as follows:
The continuity equation
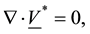 (1)
(1)
The momentum equation
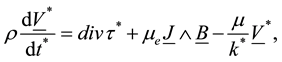 (2)
(2)
where 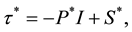 and
and
 , (3)
, (3)
where  and
and 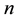 are the material parameters of the fluid. Note that for
are the material parameters of the fluid. Note that for  the fluid describes shear thinning, for
the fluid describes shear thinning, for 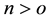 the fluid describes shear thicking, for
the fluid describes shear thicking, for 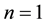 the Newtonian fluid is recovered and for
the Newtonian fluid is recovered and for 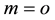 the generalized power-law model can be obtained.
the generalized power-law model can be obtained.
The temperature equation
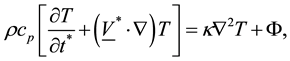 (4)
(4)
The concentration equation
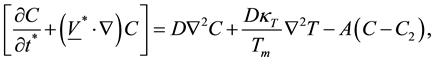 (5)
(5)
The dissipation function 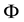
 (6)
(6)
Maxwell s equations
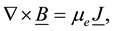 (7)
(7)
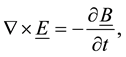
Ohm’s equation

where 



bility, 


is the electric field and 




3. Mathematical Formulation
Consider the two-dimensional motion of an incompressible Sisko fluid in an infinite channel of width


where b is the wave amplitude, 

Now, Equations (2)-(6) can be written in two-dimensional 


Figure 1. Sketch of the problem.



where




Subjected to the following appropriate boundary conditions:

Choose the wave frame 

In which 
Then, the Equations (10)-(19) can be written as:





where



The boundary conditions are:

In order to simplify the governing equations of the motion, we may introduce the following dimensionless transformations:

where, 



Substituting (30) into Equations (21)-(29) we obtain the following non-dimensional equations after dropping the star mark:








The boundary conditions are:

where, the dimensionless parameters are defined by:










By using the following definition of stream function 

The system of Equations (3.30)-(3.38) can be written as:






The boundary conditions for the dimensionless stream function in the moving frame are given by:

The dimensionless form of the surface of the peristaltic wall can be written as:
where 

4. Solution of the Problem
According to long wavelength approximation 






In order to solve the Equations (49)-(51) subjected to the boundary conditions, we suppose the following perturbation for small non-Newtonian parameter

Substituting (55) into (49)-(54) and comparing the coefficient of zero and first order of 
4.1. Zero Order System of h



With the respective boundary conditions

4.2. First Order System of h
We shall consider the case of Dielatent fluids when n > 1, and we choose (n = 3), then we have the following system of first order of



with the respective boundary conditions

4.3. Solution for System of Zero Order



4.4. Solution for System of First Order



5. Results and Discussions
The problem of the peristaltic flow of a Sisko fluid through a porous medium with heat and mass transfer has been discussed. The effects of non-Newtonian dissipation and chemical reaction on the fluid flow have been considered. We obtained the solutions of the momentum, heat and mass equations analytically by using the perturbation technique for small non-Newtonian parameter 
Figure 2 illustrates the relation between the value of stream function 



In Figure 4, the relation between the value of stream function 



Figure 5, illustrates the relation between the value of temperature 

In Figure 6, we can observe that the value of temperature increases with increasing the Prandtle number parameter




Figure 2. Stream function profiles 

Figure 3. Stream function profiles 

Figure 4. Stream function profiles 

Figure 5. Temperature profiles 

Figure 6. Temperature profiles 

Figure 7. Temperature profiles 

In Figure 8, the relation between the value of concentration 








6. Conclusion and Applications
In this work, we study the peristaltic motion of magneto-hydrodynamics flow with heat and mass transfer for incompressible non-Newtonian fluid through a porous medium. The governing partial differential equations of this problem, subjected to the boundary conditions are solved analytically by using perturbation technique. The
Figure 8. Concentration profiles 

Figure 9. Concentration profiles 

Figure 10. Concentration profiles 

Figure 11. Concentration profiles 

analytical forms for the stream distribution







The study of this phenomenon is very important, because the study of flow through porous medium has many applications. It has an important role in agricultural, extracting pure petrol from crude oil and chemical engineering. There are examples of natural porous media such as wood, filter paper, cotton, leather and plastics. As a good biological example on the porous medium, the human lung galls bladder and the walls of vessels. The peristaltic motion has been found to involve in many biological organs such as esophagus, small and large intestine, stomach, the human ureter, lymphatic vessels and small blood vessels. Also, peristaltic transport occurs in many practical applications involving biomechanical systems such as finger pumps.
Cite this paper
Nabit Tawfiq MohamedEl-Dabe,Ahmed YounisGhaly,Sallam NagySallam,KhaledElagamy,Yasmeen MohamedYounis, (2015) Peristaltic Pumping of a Conducting Sisko Fluid through Porous Medium with Heat and Mass Transfer. American Journal of Computational Mathematics,05,304-316. doi: 10.4236/ajcm.2015.53028
References
- 1. Shapiro, A.H., Jafferin, M.Y. and Weinberg, S.L. (1969) Peristaltic Pumping with Long Wave Lengths at Low Reynolds Number. Journal Fluid Mechanics, 35, 669-675.
- 2. Kaimal, M.R. (1978) Peristaltic Pumping of Non-Newtonian Fluid at Low Reynolds Number under Long Wave Approximation. Journal of Applied Mechanics, 45, 32.
http://dx.doi.org/10.1115/1.3424270 - 3. Radhakrishnamacharya, G. and Srinivasulu, C. (2007) Influence of Wall Properties on Peristaltic Transport with Heat Transfer. Comptes Rendus Mecanique, 335, 369-373.
http://dx.doi.org/10.1016/j.crme.2007.05.002 - 4. Hayat, T., Qureshi, M.U. and Hussain, Q. (2009) Effect of Heat Transfer on the Peristaltic Flow of an Electrically Conducting Fluid in a Porous Space. Applied Mathematical Modelling, 33, 1862-1873.
http://dx.doi.org/10.1016/j.apm.2008.03.024 - 5. Abd Elmaboud, Y. and Mekheimer, Kh.S. (2008) Peristaltic Flow of a Couple Stress Fluid in an Annulus: Application of an Endoscope. Physica A: Statistical Mechanics and Its Applications, 387, 2403-2415.
http://dx.doi.org/10.1016/j.physa.2007.12.017 - 6. Krishna Kumari.P, S.V.H.N., Ramana Murthy, M.V., Chenna Krishna Reddy, M. and Ravi Kumar, Y.V.K. (2011) Peristaltic Pumping of a Magnetohydrodynamic Casson Fluid in an Inclined Channel. Advances in Applied Science Research, 2, 428-436.
- 7. Ravi Kumar, Y.V.K., Krishna Kumari.P, S.V.H.N., Ramana Murthy, M.V. and Sreenadh, S. (2011) Peristaltic Transport of a Power-Law Fluid in an Assymmetric Channel Bounded by Permeable Walls. Advances in Applied Sciences, 2, 396-340.
- 8. Eldabe, N.T. and Sallam, S.N. (1998) Magenetohydrodynamic Flow and Heat Transfer in a Viscoelastic Incompressible Fluid Confined between a Horizontal Stretching Sheet and a Parallel Porous Wall. Canadian Journal of Physics, 76, 98.
http://dx.doi.org/10.1139/cjp-76-12-949 - 9. El Shehawey, E.F. and El Sebaei, W. (2000) Peristaltic Transport in a Cylindrical Tube through a Porous Medium. International Journal of Mathematics and Mathematical Sciences, 26, 217-230.
http://dx.doi.org/10.1155/S0161171200004737 - 10. El-Dabe, N.T.M., Fouad, A. and Hussein, M.M. (2010) Magnetohydrodynamic Flow and Heat Transfer for a Peristaltic Motion of Carreau Fluid through a Porous Medium. Punjab University Journal of Mathematics, 42, 1-16.
- 11. Eldabe, N.T. and Mohamed, M.A.A. (2002) Heat and Mass Transfer in Hydromagnetic Flow of the Non-Newtonian Fluid with Heat Source over an Accelerating Surface through a Porous Medium. Chaos, Solitons and Fractals, 13, 907-917.
http://dx.doi.org/10.1016/S0960-0779(01)00066-2 - 12. Srinivas, S. and Kothandapani, M. (2008) Peristaltic Transport in an Asymmetric Channel with Heat Transfer—A Note. International Communications in Heat and Mass Transfer, 35, 514-522.
http://dx.doi.org/10.1016/j.icheatmasstransfer.2007.08.011 - 13. Hayat, T., Abbasi, F.M. and Alsaedi, A. (2014a) Soret and Dufour Effects on Peristaltic Flow in an Asymmetric Channel. Arabian Journal for Science and Engineering, 39, 4341-4349.
http://dx.doi.org/10.1007/s13369-014-1163-y - 14. Hayat, T., Hina, S., Hendi, A.A. and Asghar, S. (2011) Effect of Wall Properties on the Peristaltic Flow of a Third Grade Fluid in a Curved Channel with Heat and Mass Transfer. International Journal of Heat and Mass Transfer, 54, 5126-5136.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2011.07.036 - 15. Hayat, T., Noreen, S., Alhothuali, M.S., Asghar, S. and Alhomaidan, A. (2012) Peristaltic Flow under the Effects of an Induced Magnetic Field and Heat and Mass Transfer. International Journal of Heat and Mass Transfer, 55, 443-452.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2011.09.044 - 16. Eldabe, N.T., Hassan, A.A. and Mohamed, M.A.A. (2003) Effect of Couple Stresses on the MHD of a Non-Newtonian Unsteady Flow between Two Parallel Porous Plates. Zeitschrift für Naturforschung, 58, 204-210.
http://dx.doi.org/10.1515/zna-2003-0405
Appendix






















