Finite Element Method for a Kind of Two-Dimensional Space-Fractional Diffusion Equation with Its Implementation

doi:10.4236/ajcm.2015.52012

American Journal of Computational Mathematics
Vol.05 No.02(2015), Article ID:57027,22 pages
10.4236/ajcm.2015.52012

Beiping Duan, Zhoushun Zheng^*, Wen Cao

●How to Cite this Article

School of Mathematics and Statistics, Central South University, Changsha, China

Email: ^*zheng@163.com

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

Received 6 May 2015; accepted 5 June 2015; published 10 June 2015

ABSTRACT

In this article, we consider a two-dimensional symmetric space-fractional diffusion equation in which the space fractional derivatives are defined in Riesz potential sense. The well-posed feature is guaranteed by energy inequality. To solve the diffusion equation, a fully discrete form is established by employing Crank-Nicolson technique in time and Galerkin finite element method in space. The stability and convergence are proved and the stiffness matrix is given analytically. Three numerical examples are given to confirm our theoretical analysis in which we find that even with the same initial condition, the classical and fractional diffusion equations perform differently but tend to be uniform diffusion at last.

Keywords:

Galerkin Finite Element Method, Symmetric Space-Fractional Diffusion Equation, Stability, Convergence, Implementation

1. Introduction

Fractional convection-diffusion equations are generalizations of classical convection-diffusion equations, which have come to be applied in Physics [1] -[4] , hydrology [5] [6] and many other fields. As it is difficult to get the analytic solutions of these equations, numerical approaches to different type of fractional convection-diffusion equations are proposed in recent years. Tadjeran et al. [7] considered one-dimensional space-fractional diffusion equation with variable coefficient by fractional Crank-Nicholson method based on the shifted Grünwald formula, and obtained an unconditional stable second-order accurate numerical approximation by extrapolation. Later, Tadjeran and Meerschaert [8] utilized the classical alternating directions implicit (ADI) approach with a Crank- Nicholson discretization and a Richardson extrapolation to solve two-dimensional space-fractional diffusion equation, and proved it is unconditional stable second-order accurate. Sousa [9] derived an implicit second-order accurate numerical method which used a spline approximation for space-fractional diffusion equation and the consistency and stability were examined. A space-time spectral method for time fractional diffusion equation was developed by Li and Xu [10] , in which the convergence was proven and priori error estimate was given. Xu [11] proposed a discontinuous Galerkin method for one-dimensional convection-subdiffusion equations with fractional Laplace operator and derived stability analysis and optimal convergence rate. Jin et al. [12] gave a full discretization scheme for multi-term time-fractional diffusion equation by using finite difference method in time and finite element method in space, and discussed its stability and error estimate.

The symmetric space-fractional convection-diffusion equation (including both left and right derivatives) was firstly proposed by Chaves [13] to investigate the mechanism of super-diffusion and was later generalized by Benson et al. [14] [15] . It is a powerful approach for a description of transport dynamics in complex systems governed by anomalous diffusion. Zhang [16] et al. considered one-dimensional symmetric space-fractional partial differential equations with Galerkin finite element method in space and a backward difference technique in time, and the stability and convergency were proven. Sousa [17] derived a second order numerical method for one-dimensional symmetric space-fractional convection-diffusion equation and studied its convergence.

Recently, numerical methods for multi-dimensional problems of fractional differential equational are studied. For example, in [18] , a semi-alternating direction method for a 2-D fractional reaction diffusion equation are proposed to solve FitzHugh-Nagumo model on an approximate irregular domain. In [19] , Crank-Nicolson ADI spectral method is presented to approximate the two-dimensional Riesz space fractional nonlinear reaction- diffusion equation. In [20] [21] , Wang and Du proposed fast finite difference methods to compute three-dimen- sional space-fractional diffusion equations, which reduce the computational cost a lot.

In this paper, we consider the following two-dimensional symmetric space-fractional diffusion equation (SSFDE)

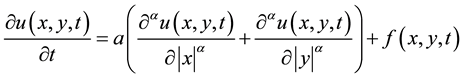(1)

where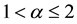, 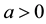is a constant, 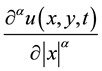and 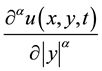are Riesz fractional derivatives defined as follows

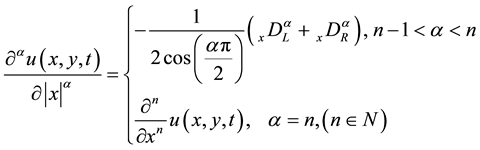
Remark: In this paper, the default fractional derivative is Riemann-Liouville derivative.

This article is organized as follows. In Section 2, we introduce some functional spaces. In Section 3 and Section 4, we prove existence and uniqueness of the variational solution. The full discretization of SSFDE is given in Section 5, where we apply Crank-Nicolson technique in time and Galerkin finite element method in space. Moreover, a detailed stability and convergence analysis is carried out. In section 6, we present the imple- mentation of how to get the stiffness matrix. Finally, some numerical examples are given in Section 7 to confirm our theretical analysis and to compare the difference between fractional diffusion and integer order diffusion system.

2. Two-Dimensional Fractional Derivative Spaces

Ervin and Roop [22] had given the definitions of one-dimensional fractional derivative spaces, and later were generalized to via fractional directional integral and derivative in [23] . Here we present some definitions and theorems needed in this paper.

Definition 2.1 (Directional Integral [23] ). Let, be given. The mth order fractional integral in the direction of 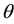is given by

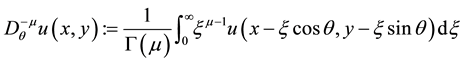(2)

Definition 2.2 ([23] ). Let, 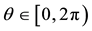be given. The nth order derivative in the direction of is given by

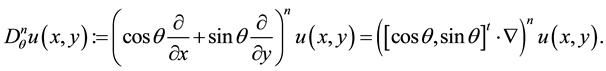(3)

Definition 2.3 (Directional Derivative [23] ). Let, be given. Let n be the smallest integer then, , and define. Then the mth order directional derivative in the direction of is defined by

(4)

Definition 2.4 ([23] ). Let, be given. Define the semi-norm

and norm

(5)

and let denote the closure of with respect to

Definition 2.5 ([23] ). Let, , , be given as before. Define the semi-norm

and norm

(6)

and let denote the closure of with respect to

Theorem 2.1 ([23] ). Let, , , be given. Then the spaces and are equal, with equivalent semi-norms and norms.

Theorem 2.2 ([23] ). For, we have

(7)

Definition 2.6 ([23] ). Let and. Define the semi-norm

and norm

(8)

where denotes the Fourier tansform of u with variable. Also let denote the closure of with respect to.

In the following, a semi-norm is defined by integral with respect to the probability measure. And

(9)

holds independent of the value of.

Remark: The condition holds if is atomic with at least two atoms, , such that. In this case, (9) reduces to [23]

which is positive for all such if and only if for some i and j.

Definition 2.7 ([23] ) For, define the semi-norm

and norm

(10)

and let denote the closure of with respect to.

Theorem 2.3 ([23] ). Let M satisfy (9). Then the spaces and are equivalent with equivalent semi-norms and norms.

Theorem 2.4 (Fractional Poincarà Friedrichs Inequality [23] ). For, we have

(11)

The definitions and theorems above are basic frame of multi-dimensional fractional derivative spaces. In terms of Equation (1), we let M be atomic with atoms or, then the semi- norm and norm of can be defined in the following way:

Definition 2.8 Let, define the semi-norm

(12)

(13)

and norm

(14)

It is easy to derive that (12) is equivalent to (13) with using theorem 2.1 and Parseval equality.

Lemma 2.1 (The relationship between R-L and Caputo fractional order derivatives [24] ). Assume that the derivatives are continuous in the closed interval and, then

(15)

where denotes Caputo fractional order derivative, which is defined as

So when for, the two kinds of derivates is equivalent, i.e.

(16)

And if for, there have.

Lemma 2.2 ([24] ). If and, then

(17)

So, if for, associating with Lemma 2.1 and the definition of Caputo fractional derivative, it is easy to obtain that

(18)

Lemma 2.3 (Adjoint Property). The left and right Riemann-Liouville fractional integral operator are adjoints in the sense, i.e., for all,

(19)

Theorem 2.5 Let, , and if for, for , then

(20)

Proof. Let, combining Lemma 2.2 and Lemma 2.3 we have

From Lemma 2.1, we know if for, then. So we have

(21)

For convenience, we denote

(22)

then Equation (1) can be written in the following form

(23)

where, is an open convex subset.

To derive the variational form of (23), we introduce two properties of firstly.

Property 1 (Fourier Transform of) If, then the Fourier Transform of is

(24)

where denotes the Fourier Transform of v,

(25)

Proof. In view of Theorem 2.1, we can derive the Fourier Transform

Therefore, we have

Remark: Here, we use to make difference from the fractional Laplace operator, which defined as [25] [26] and its Fourier Transform is, where.

Property 2 If, , then

(26)

where

In fact, when, the formula is the classical Green formula.

Proof. Using Theorem 2.5 and taking notice that and, , we have

3. Variational Formulation

In order to derive the variational form of (23), we assume u is a sufficiently smooth solution of (23), and multiply by arbitrary to obtain

(27)

The weak formulation of the equation is to find the which can make the following equation established

(28)

With using property 2, the above formula could be written as

Thus we define the associated bilinear form as

(29)

Theorem 3.1 The form defined by (29) is continuous and coercive.

Proof. According to the definition of,

Using Cauchy-Schwarz inequality we can obtain

Associating the definition of the semi-norm of and using Young’s inequality it follows

So we have

Combining the equivalence of and, we have

i.e., the form is continuous on. Replacing v with u in (29), we have

According to the equivalence of and, and combining Theorem 2.4 we can obtain

(30)

i.e., the form is coercive on.

Theorem 3.2 (Energy Inequality). If, , and

, where. Then, we can obtain the energy estimate

(31)

i.e. the solution of (23) is well posed.

Proof. Multiply the first formula of (23) by u and integrate both sides of the equation in, then we have

As the coercivity of the form and Young’s inequality, we obtain

Take and integrating over, to the above inequality we get

Corollary. The solution of variational formulation (28) exists and is unique.

Proof. The existence can be derived directly from Theorem 3.6 with Lax-Milgram theorem and Theorem 3.7 ensure the uniqueness.

4. Crank-Nicolson-Galerkin Finite Element Fully Discrete System

Let denote a uniform of partition of, with grid parameter h, and. denote the continuous functions on G. We define the finite dimensional subspace

with the piecewise polynomials of order or less then k. Taking a uniform mesh for the time variable t and let

where being the time step, and. Then by the Galerkin finite element method and Crank- Nicolson technique, (23) is transformed into the following problem: find such that

(32)

hold for each, where is a suitable approximation of initial data.

Theorem 4.1 For and, the fully discrete scheme (32) has a unique solution.

Proof. Assume that. Then the first formula of (32) can be written as

(33)

In view of Theorem 4.1, we have

and

Therefore, the bilinear form is continuous over and coercive over. Furthermore,

i.e., the right side of (33) is continuous. According to Lax-Milgram theorem, the fully discrete approximating system (32) has unique solution.

Theorem 4.2 (Energy Inequality). If then the fully discrete approximating system (32) is unconditionally stable and satisfies

(34)

Proof. Taking in (32), noticing the coercivity of the bilinear form and employing Hölder inequality, we have

Then we can obtain

So the result is valid.

Lemma 4.1 (Approximation Property [27] ) Let, then there exists a constant depending only on such that

(35)

where is a projection operator.

Theorem 4.3 (Convergence). Assume that, , and u satisfies, , Then satisfies

(36)

Proof. Let

where is the elliptic projection operator from into which is defined as follows for each:

(37)

Define, then

Looking back to the first formula of (32), we can derive

Noting that

holds for, and with using (37), we can obtain

Taking, noting and combining Cauchy-Schwarz inequality, we can obtain

So we have

In the following we will estimate the three parts of the above inequality respectively. The first part

satisfies

The second part satisfies

The third part satisfies

Hence we can obtain a recursive inequality

Summing up from 1 to then

(38)

Take in (35), then we can obtain

(39)

From (38) and (39), we can derive the following error estimate

(40)

Finally, the formula (40) leads to (36).

5. Computational Implementation

Since the fractional derivative is a non-local operator, the implementation of finite element method for fractional differential equations is very complex. The main problem is how to obtain the stiffness matrix. In [28] , Roop investigated the computational aspects of the Galerkin approximating using continuous piecewise polynomial basis functions on a regular triangulation of the domain. In this section we give the computational details, in which the bilinear functions are chosen as the basis functions. The computational domain is and the number of computational grid is.

First of all, we consider the problem of finding the fractional derivative of each of the basis function. The support set of the ith basis function is (see Figure 1). It is defined as

Figure 1. Sketch for the element and node number.

where are the centers of the blocks, and,. Assume the coordinate of the ith node (see Figure 1) is, then we can derive

(41)

If, we have

If, taking notice that, we can get

If, we have

For, and, replacing by in the three cases above respectively, we can get in the corresponding region.

Secondly, we consider the problem of calculating the inner product for a fixed i and

, where is the number of inner points. Denote

(42)

then the coordinate of the jth node is.

It is easy to know when or,. For the other cases, we present the results here. Please see the appendix for the expatiation.

Case 1:, or, i.e. or

Case 2:, or, i.e. or

Case 3:, or, i.e. or

Case 4:, or, i.e. or

Case 5:, i.e.

Case 6:, i.e.

Case 7:, i.e.

Case 8:, i.e.

Finally, we consider the problem of calculating the stiffness matrix A via the inner product obtained. Form Equation (29) we can see that A can be decomposed into four parts. With ignoring the coefficient

we denote

then it is obvious that, , namely,.

In fact, for and, if we start numbering these nodes along the direction of y axis and rename the two basis functions to and, then we have

(43)

where are defined in (41) and (42).

(44)

which means can be derived from case 1 to case 8 we have presented above with exchanging and, and. And if, Equation (44) will reduce to

(45)

6. Numerical Experiments

Example 1. Consider the following problem:

Which has exact solution, and

Obviously,. We take and 1.9 respectively, then present corresponding experimental error and convergence rate in norm in Table 1 with, ,. To display the numerical solution and error visually, we present the surfaces of and at in Figure 2 and Figure 3 with.

Remark: The trial function in all of the numerical experiments is bilinear function.

We can see that the results support our error estimate and ensure the numerical approximation is effective. In the following, we take fixed initial value and source term independent of to try to describe the character of the solution with the change of.

Example 2. Consider the following problem

Table 1. Experimental error and convergence rate in norm.

Figure 2. Numerical solution (left) and error (right) for α = 1:6 at t = 0.5.

Figure 3. Numerical solution (left) and error (right) for α = 1:9 at t = 0.5.

Let and we know if the equation reduces to classical diffusion equation which has exact solution. Now, we take, , , and respectively to show the character of the system in Figure 4 and Figure 5. From the numerical experiments we conclude that the bigger is, the smaller is. I.e., the process of diffusion becomes faster on the whole.

Example 3. In order to compare the difference between fractional diffusion and classical diffusion, consider the following equation with homogeneous boundary condition:

Figure 4. Numerical solution for α = 1:1 (left) and α = 1:4 (right).

Figure 5. Numerical solution for α = 1:7 (left) and α = 1:99 (right).

where u represents concentration and the diffusion coefficient is. The initial value of u satisfies

which means the initial concentration concentrates in a rhombus. We take and in the above equation respectively, then plot isolines at and in the fol- lowing images of Figure 6 (on the left side and on the right side).

Figure 6. Contour maps of α = 1:4 (left) and α = 2 (right) at specified time.

We note that the initial condition in the fractional system affect wider area than integer order in a short period of time by comparing the first two contour maps. Moreover, the diffusion under the influence of initial condition last longer in the fractional system. So at, the diffusion in classical system is almost uniform in every direction but this state needs more time to reach in the fractional system (see the left map at).

7. Conclusion

Many different numerical methods for fractional convection-diffusion equation have been discussed by researchers in recent 10 years. In this paper, we discussed one kind of space-fractional diffusion equation which could be derived through replacing the second order derivative of x and y by corresponding Riesz fractional derivative in the classical diffusion equation. A numerical approximation for the equation was presented by using C-N tech- nique in time direction and Galerkin finite method in space. Furthermore, a detailed stability and convergence analysis was carried out for the fully discrete system. Then, some numerical examples were given and the dif- ferences between fractional and classical diffusion were presented. It is known that the stiffness matrix of frac- tional differential equation is rather complex, so to make the approach applicatory. We give the implementation of computational aspect. However, because of the non-local property of fractional derivative, the stiffness matrix is not sparse (almost dense) which challenges the computational resources.

Acknowledgements

The authors were supported by the National Natural Science Foundation of China under Project 51174236, and the National Basic Research Program of China under Project 2011CB606306.

References

Metzler, R. and Klafter, J. (2004) The Restaurant at the End of the Random Walk: Recent Developments in the Description of Anomalous Transport by Fractional Dynamics. Journal of Physics A: Mathematical and General, 37, R161- R208. http://dx.doi.org/10.1088/0305-4470/37/31/R01
Zaslavsky, G.M., Stevens, D. and Weitzner, H. (1993) Self-Similar Transport in Incomplete Chaos. Physical Review E, 48, 1683-1694. http://dx.doi.org/10.1103/PhysRevE.48.1683
Metzler, R. and Klafter, J. (2000) The Random Walk’s Guide to Anomalous Diffusion: A Fractional Dynamics Approach. Physics Reports, 339, 1-77. http://dx.doi.org/10.1016/S0370-1573(00)00070-3
Zaslavsky, G.M. (2002) Chaos, Fractional Kinetics, and Anomalous Transport. Physics Reports, 371, 461-580. http://dx.doi.org/10.1016/S0370-1573(02)00331-9
Schumer, R., Benson, D.A., Meerschaert, M.M. and Baeumer, B. (2003) Multiscaling Fractional Advection-Dispersion Equations and Their Solutions. Water Resources Research, 39, 1022-1032. http://dx.doi.org/10.1029/2001WR001229
Schumer, R., Benson, D.A., Meerschaert, M.M. and Wheatcraft, S.W. (2001) Eulerian Derivation of the Fractional Advection-Dispersion Equation. Journal of Contaminant Hydrology, 48, 69-88. http://dx.doi.org/10.1016/S0169-7722(00)00170-4
Tadjeran, C., Meerschaert, M.M. and Scheffler, H.P. (2006) A Second-Order Accurate Numerical Approximation for the Fractional Diffusion Equation. Journal of Computational Physics, 213, 205-213. http://dx.doi.org/10.1016/j.jcp.2005.08.008
Tadjeran, C. and Meerschaert, M.M. (2007) A Second-Order Accurate Numerical Method for the Two-Dimensional Fractional Diffusion Equation. Journal of Computational Physics, 220, 813-823. http://dx.doi.org/10.1016/j.jcp.2006.05.030
Sousa, E. (2011) Numerical Approximations for Fractional Diffusion Equations via Splines. Computers and Mathematics with Applications, 62, 938-944. http://dx.doi.org/10.1016/j.camwa.2011.04.015
Li, X. and Xu, C. (2009) A Space-Time Spectral Method for the Time Fractional Diffusion Equation. SIAM Journal on Numerical Analysis, 47, 2108-2131.
Xu, Q. and Hesthaven, J.S. (2013) Discontinuous Galerkin Method for Fractional Convection-Diffusion Equations. http://arxiv.org/abs/1304.6047
Jin, B., Lazarov, R., Liu, Y. and Zhou, Z. (2015) The Galerkin Finite Element Method for a Multi-Term Time-Fractional Diffusion Equation. Journal of Computational Physics, 281, 825-843. http://dx.doi.org/10.1016/j.jcp.2014.10.051
Chaves, A.S. (1998) A Fractional Diffusion Equation to Describe Lévy Flight. Physics Letters A, 239, 13-16. http://dx.doi.org/10.1016/S0375-9601(97)00947-X
Benson, D.A., Wheatcraft, S.W. and Meerschaert, M.M. (2000) Application of a Fractional Advection-Dispersion Equation. Water Resources Research, 36, 1403-1412. http://dx.doi.org/10.1029/2000WR900031
Benson, D.A., Wheatcraft, S.W. and Meerschaert, M.M. (2000) The Fractional Order Governing Equation of Lévy Motion. Water Resources Research, 36, 1413-1423. http://dx.doi.org/10.1029/2000WR900032
Zhang, H., Liu, F. and Anh, V. (2010) Galerkin Finite Element Approximation of Symmetric Space-Fractional Partial Differential Equations. Applied Mathematics and Computation, 217, 2534-2545. http://dx.doi.org/10.1016/j.amc.2010.07.066
Sousa, E. (2012) A Second Order Explicit Finite Difference Method for the Fractional Advection Diffusion Equation. Computers and Mathematics with Applications, 64, 3141-3152. http://dx.doi.org/10.1016/j.camwa.2012.03.002
Liu, F., Zhuang, P., Turner, I., Anh, V. and Burrage, K. (2015) A Semi-Alternating Direction Method for a 2-D Fractional FitzHugh-Nagumo Monodomain Model on an Approximate Irregular Domain. Journal of Computational Physics, 293, 252-263.
Zeng, F., Liu, F., Li, C., Burrage, K., Turner, I. and Anh, V. (2014) Crank-Nicolson ADI Spectral Method for the Two- Dimensional Riesz Space Fractional Nonlinear Reaction-Diffusion Equation. SIAM Journal on Numerical Analysis, 52, 2599-2622. http://dx.doi.org/10.1137/130934192
Wang, H. and Du, N. (2013) A Fast Finite Difference Method for Three-Dimensional Time-Dependent Space-Fractional Diffusion Equations and Its Efficient Implementation. Journal of Computational Physics, 253, 50-63. http://dx.doi.org/10.1016/j.jcp.2013.06.040
Wang, H. and Du, N. (2014) Fast Alternating-Direction Finite Difference Methods for Three-Dimensional Space- Fractional Diffusion Equations. Journal of Computational Physics, 258, 305-318. http://dx.doi.org/10.1016/j.jcp.2013.10.040
Ervin, V.J. and Roop, J.P. (2006) Variational Formulation for the Stationary Fractional Advection Dispersion Equation. Numerical Methods for Partial Differential Equations, 22, 558-576. http://dx.doi.org/10.1002/num.20112
Ervin, V.J. and Roop, J.P. (2007) Variational Solution of Fractional Advection Dispersion Equations on Bounded Domains in R^d. Numerical Methods for partial Differential Equations, 23, 256-281. http://dx.doi.org/10.1002/num.20169
Podlubny, I. (1999) Fractional Differential Equations. Academic Press, Waltham.
Muslih, S.I. and Agrawal, O.P. (2010) Riesz Fractional Derivatives and Fractional Dimensional Space. International Journal of Theoretical Physics, 49, 270-275. http://dx.doi.org/10.1007/s10773-009-0200-1
El-Sayed, A.M.A. and Gaber, M. (2006) On the Finite Caputo and Finite Riesz Derivatives. Electronic Journal of Theoretical Physics, 3, 81-95.
Brenner, S. and Scott, L.R. (1994) The Mathematical Theory of Finite Element Methods. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4757-4338-8
Roop, J.P. (2006) Computational Aspects of FEM Approximation of Fractional Advection Dispersion Equations on Bounded Domains in R². Journal of Computational and Applied Mathematics, 193, 243-268.

Appendix

Here, we give the computational details of case 5 to case 8. It is analogous for case 1 to case 4. To begin with, we introduce one formula which is used frequently in the procedure of computing the inner product and can be derived directly from the definition of beta function by integral transformation: