American Journal of Computational Mathematics
Vol.3 No.4(2013), Article ID:40965,7 pages DOI:10.4236/ajcm.2013.34044
Dispersion Effect on Traveling Wave Solution of K-dV Equation
1Department of Mathematics, Jagannath University, Dhaka, Bangladesh
2Department of Mathematics, BUET, Dhaka, Bangladesh
3Department of Mathematics, Jahangirnagar University, Savar, Bangladesh
Email: rrezaul@yahoo.com, maalim@math.buet.ac.bd, andallahls@gmail.com
Copyright © 2013 Rezaul Karim et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received October 13, 2013; revised November 13, 2013; accepted November 20, 2013
Keywords: Dispersion; Temporal Independent; Propagate; Solitary Wave; Nonhydrostatic
ABSTRACT
All solutions of the Korteweg-de Vries(K-dV) equation that are bounded on the real line are physically relevant, depending on the application area of interest. Usually, both analytical and numerical approaches consider solution profiles that are either spatially localized or (quasi) periodic. The development of numerical techniques for obtaining approximate solution of partial differential equations has very much increased in the finite element and finite difference methods. Recently, new auxiliary equation method introduced by PANG, BIAN and CHAO is applied to the analytical solution of K-dV equation and wavelet methods are applied to the numerical solution of partial differential equations. Pioneer works in this direction are those of Beylkin, Dahmen, Jaffard and Glowinski, among others. In this research we employ the new auxiliary equation method to obtain the effect of dispersion term on travelling wave solution of K-dV and their numerical estimation as well. Our approach views the limit behavior as an invariant measure of the fast motion drifted by the slow component, where the known constants of motion of the fast system are employed as slowly evolving observables; averaging equations for the latter lead to computation of the characteristic features of the motion.
1. Introduction
The Korteweg-de Vries (K-dV) equation is one of the most studied nonlinear partial differential equations. It can be written as
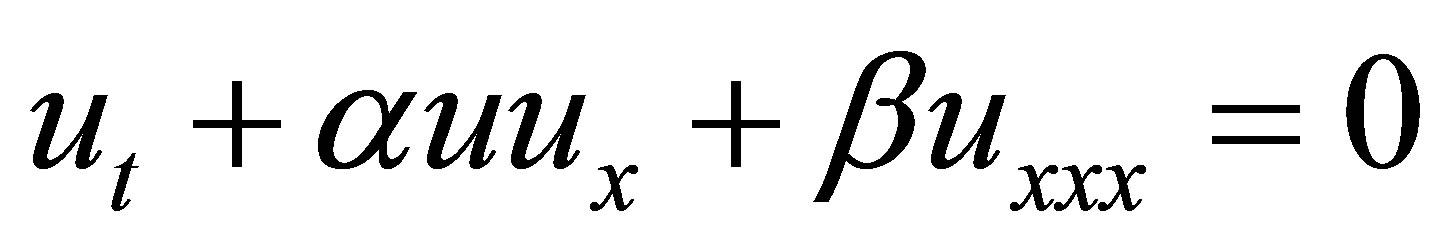 (1)
(1)
where x and t represent a scaled spatial and temporal independent variable respectively; u(x, t) is the function to be determined and for some constants α and β. The K-dV equation arises in the study of long water waves in shallow water, ion-acoustic waves in plasmas, and in general, describes the slow evolution of long waves in dispersive media [1]. The governing equation appears in the study of waves in shallow water in the fluid dynamics [2-4]. K-dV equation satisfies the property that the nonlinear term 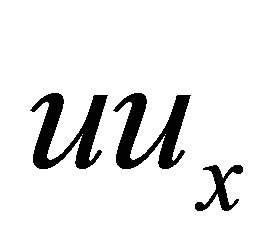 and the dispersion term
and the dispersion term 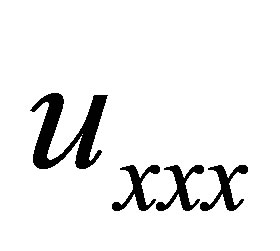 balance each other thereby generating wave solution which propagates maintaining same form throughout. The term soliton was coined by Zabusky and Kruskal to describe this solitary wave, solution of the K-dV equation [2,5,6].
balance each other thereby generating wave solution which propagates maintaining same form throughout. The term soliton was coined by Zabusky and Kruskal to describe this solitary wave, solution of the K-dV equation [2,5,6].
The importance of the equation partially derives from how well its solutions match experimental observations [7-9]. Recent work on the numerical evaluation of solutions other than solitons has allowed for the detailed study of other important classes of solutions, such as dispersive tails [10] or (quasi-) periodic multi-phase solutions, the so-called finite-genus solutions. Dispersion, a characteristic of nonlinear or nonhydrostatic waves, occurs when the wave speed is a non-constant function of the wave amplitude or wave frequency (or similarly wavelength) [11]. Distinction is sometimes made between these two types of dispersion, namely amplitude dispersion and frequency dispersion, respectively [12]. The two are synonymous with nonlinearity and nonhydrostasy in studies of gravity waves, and hence are typically called nonlinearity and dispersion. Interesting wave phenomena exist when both nonlinearity and dispersion occur together and with approximately equal magnitude. Under such circumstances, nonlinear steepening balances dispersive spreading, and propagating waves of constant form known as “solitary” wave are possible [13]. The most common equation satisfying the balanced motion includes the Boussinesq equation [14-16] and the K-dV equation. These equations represent the depth-averaged conservation of mass and momentum and include dispersive effects due to nonhydrostasy by retaining the lowest-order effects of integrating the nonhydrostatic pressure over the depth. The K-dV equation reduces conservation of mass and momentum to a single equation which is valid only for unidirectional wave propagation. Although not as computationally expensive, the primitive equation do not resolve physical dispersion resulting from nonhydrostatic effects. However, this may not be a problem when physical dispersion is negligible. As we will show, it is not only the lack of physical dispersion that adversely influences model results of internal waves, but the presence of numerical dispersion. The concept of numerical dispersion is not particularly new. The effects of numerical dispersion have received limited attention in the literature on gravity waves. One instance is from Burwell’s work [17], who examines the numerically diffusive and dispersive properties of tsunami models and finds out that the horizontal grid resolution is critical to accurately simulate the dispersive behavior. Schroeder and Schlunzen [18] drive a numerical dispersion relation for an atmospheric internal gravity wave model. Their relation naturally tends toward the true dispersion relation as the horizontal grid spacing approaches zero. In simulations of internal waves, numerical dispersion is particularly adverse because it may create an artificial balance with the nonlinear steepening tendency of the wave and produce solitary-like waves that are physically unrealistic or impossible. The goal of this research is computational investigation of dispersion term for K-dV equation analytically and numerically. In this research, we determine the auxiliary equation method to obtain the effect of dispersion term on travelling wave solution of K-dV and their numerical estimation as well. Such analyses would be of limited use without, as a point of comparison, the physical dispersion coefficient.
2. The Physical Configuration of K-dV Equation
Traveling wave flow on a channel of depth h0 of long water wave in two dimensional third order K-dV equation. In presence of acceleration due to gravity g, dispersion of wave, symmetry property and water wave theory have been investigated. (x, t) are the dispersion and water wave components along (X, Y) axes, u(x, t) represents the displacement of water wave against time and displacement. The physical configuration is as shown in Figure 1.
3. Dispersion Term Analysis
In the early days of mathematical modeling of water

Figure 1. Physical Configuration of K-dV Equation.
waves, it was assumed that the wave height was small compared to the water depth, which leads to linear dispersive equations a representative model of which is
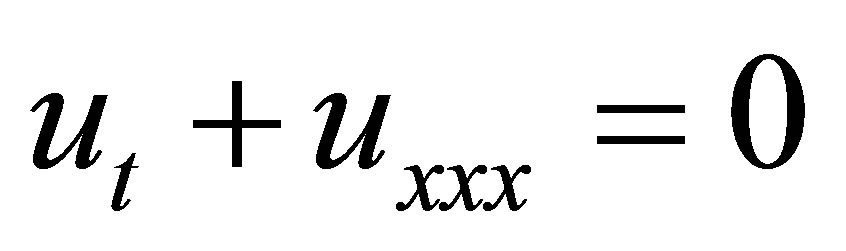 (2)
(2)
Such equations are somewhat satisfying in this regard because they have solutions that resemble waves traveling along with constant speed and fixed profile along the water surface, just like one sees in nature. To find them, we go into a moving frame with speed c by introducing new variables ξ = x − ct and τ = t, and then we seek solutions of the resulting equation that are independent of τ:

Therefore,
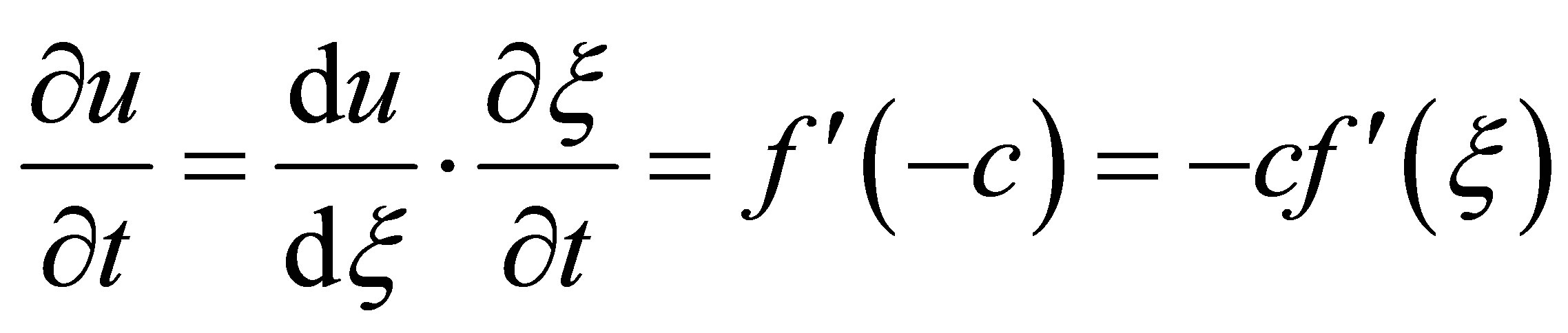
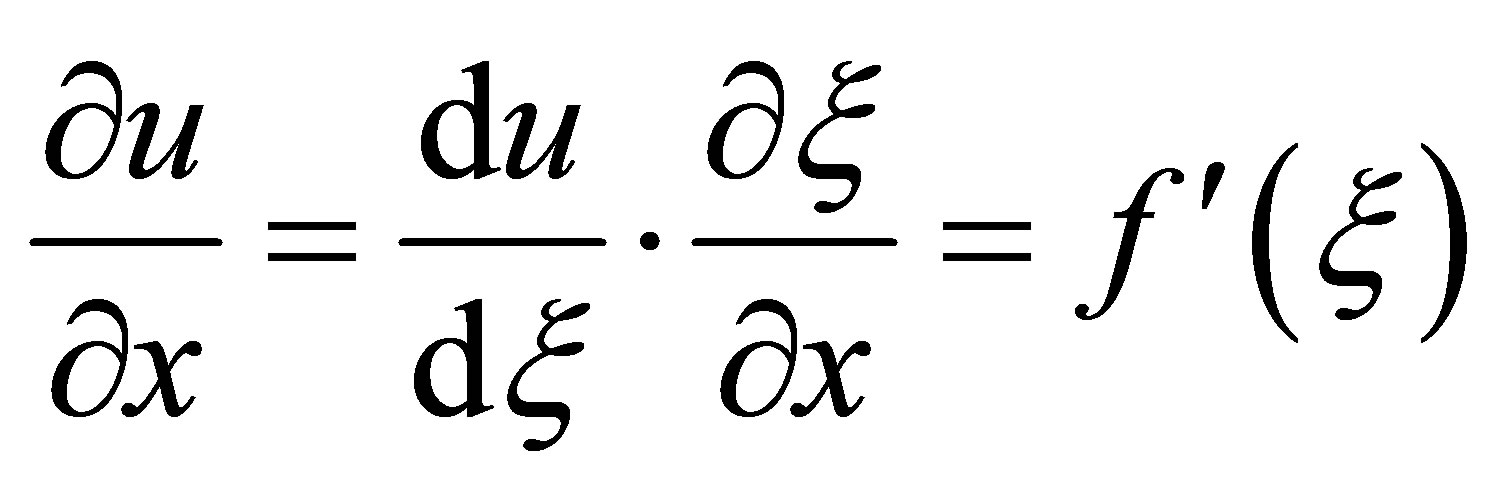

Now from the Equation (2) we get-

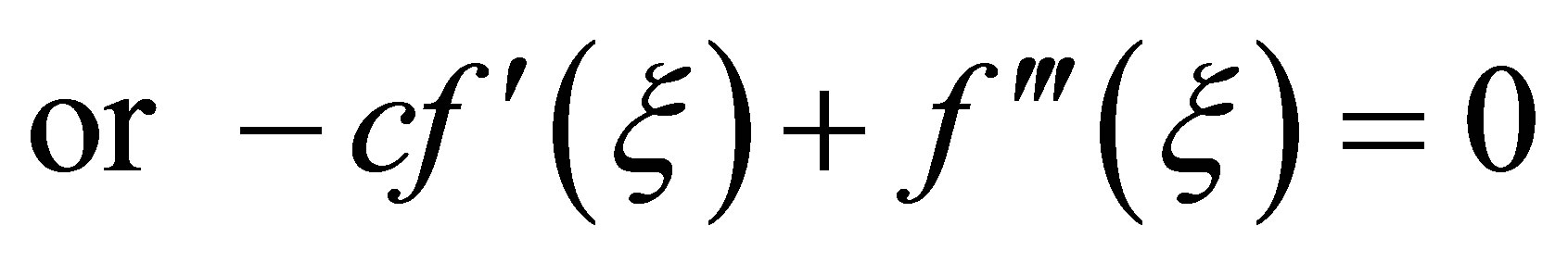
Integrating once, 
where B is an integration constant. If , then f will be bounded as a function of ξ. Then
, then f will be bounded as a function of ξ. Then
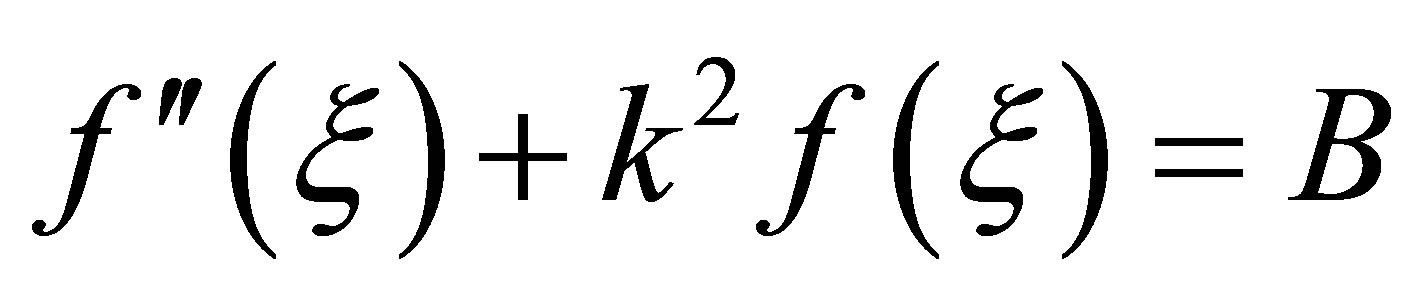 (3)
(3)
Let , therefore the auxiliary equation of the homogeneous part of the differential Equation (2) is
, therefore the auxiliary equation of the homogeneous part of the differential Equation (2) is 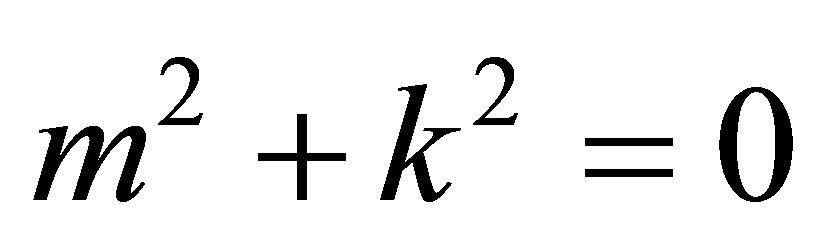 and hence the complementary function of the differential Equation (3) is as follows-
and hence the complementary function of the differential Equation (3) is as follows-
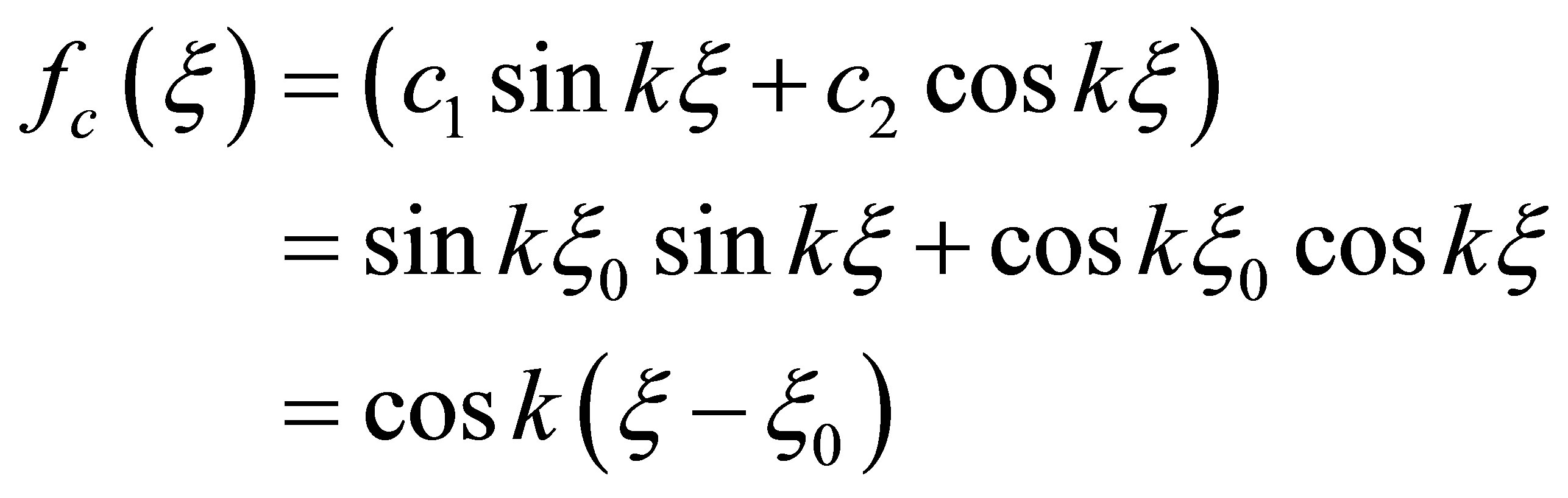
Where 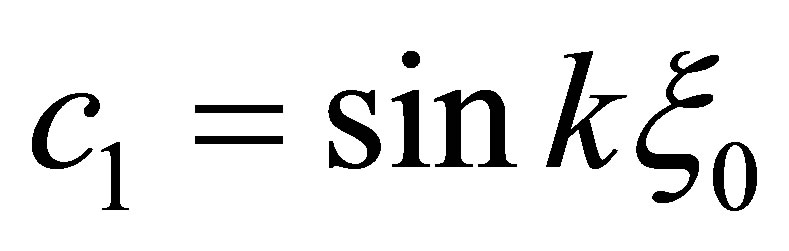 and
and 
Particular integral of the differential equation is
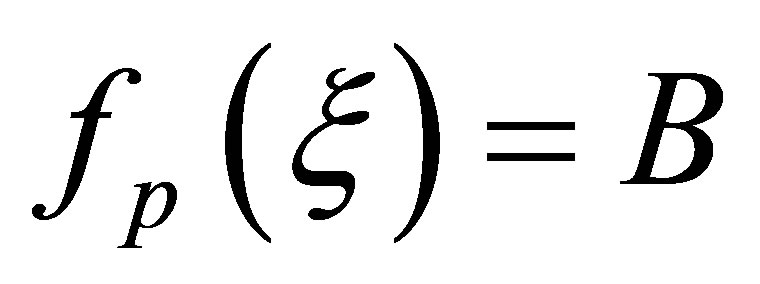 , which implies that from the differential Equation (3) is
, which implies that from the differential Equation (3) is  and hence the general solution of the differential equation is-
and hence the general solution of the differential equation is-
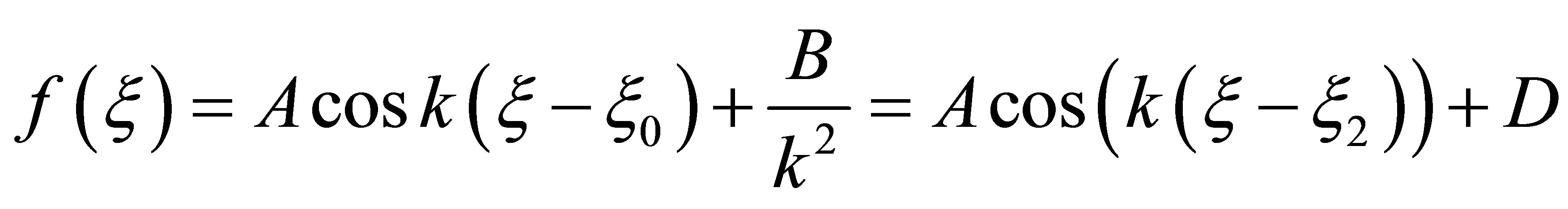
Therefore,
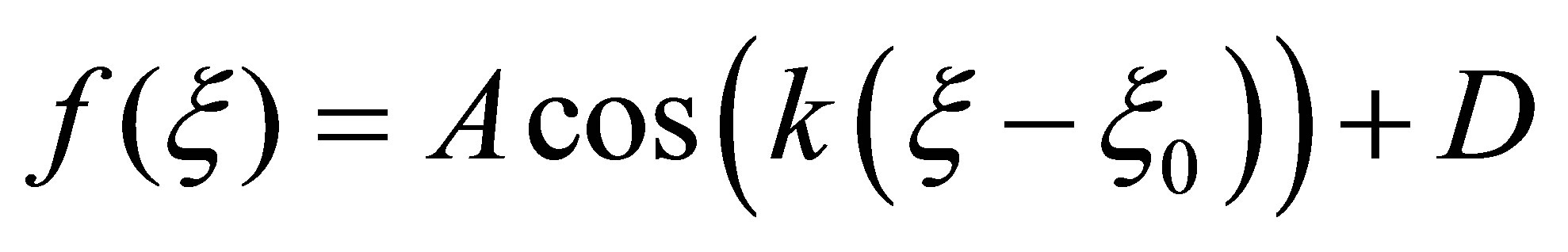 (4)
(4)
where D is another arbitrary constant. Thus, the family of bounded traveling wave solutions to this linear equation is exhausted by periodic sinusoidal wave shapes. The speed of propagation depends on the wave number k, since . (Note that these wave all propagate to the left only.) There is a lot that can be built out of these waves by superposition (it is a linear equation) but the basic point of view at this time in history was that the only waves that travel along at a constant speed without changing their form were periodic trains of waves.
. (Note that these wave all propagate to the left only.) There is a lot that can be built out of these waves by superposition (it is a linear equation) but the basic point of view at this time in history was that the only waves that travel along at a constant speed without changing their form were periodic trains of waves.
4. Results and Discussion
In the following discussion, several aspects of the numerical dispersion will be studied based on group velocity (4). We plot the numerical dispersion at moving frame with speed , and some constants a = 4.0, D = 0.8 and
, and some constants a = 4.0, D = 0.8 and 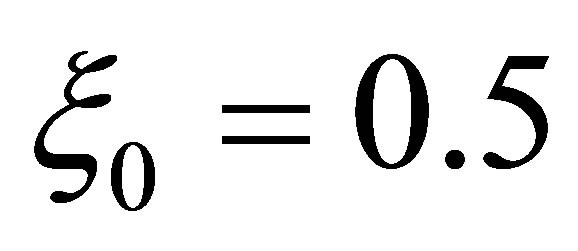 against t for different values of x in Figure 2(a)" target="_self">Figure 2(a). The numerical dispersions are always same at every point of x for a particular wave speed. Figure 2(b)" target="_self">Figure 2(b)shows the numerical dispersion relation f against x for different values of t with same speed and numerical constants. Here we see that the numerical dispersions are same at every point of time against x. Dispersion contour f against x and t shows in Figure 2(c)" target="_self">Figure 2(c). Dispersion contour has a smooth relation against x and t that is every position and moment have the same contour and for a particular speed of travelling wave in the same frame. Next we investigate the dispersion f at different values of x with speed c = −4.0, numerical constants a = 4.0, D = 0.8 and
against t for different values of x in Figure 2(a)" target="_self">Figure 2(a). The numerical dispersions are always same at every point of x for a particular wave speed. Figure 2(b)" target="_self">Figure 2(b)shows the numerical dispersion relation f against x for different values of t with same speed and numerical constants. Here we see that the numerical dispersions are same at every point of time against x. Dispersion contour f against x and t shows in Figure 2(c)" target="_self">Figure 2(c). Dispersion contour has a smooth relation against x and t that is every position and moment have the same contour and for a particular speed of travelling wave in the same frame. Next we investigate the dispersion f at different values of x with speed c = −4.0, numerical constants a = 4.0, D = 0.8 and 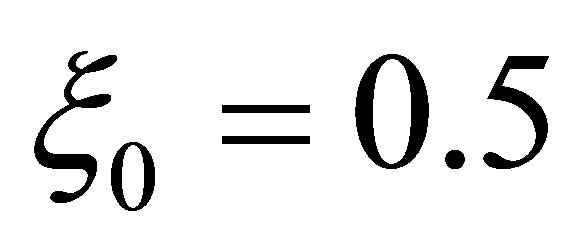 in Figure 3(a)" target="_self">Figure 3(a). Since the time step is the unconditionally stable in the scheme (4), so no longer restricted by the numerical constants, it is important and meaningful to see how a large time step impacts on numerical dispersion. Numerical dispersion f against t for different values of x shows in Figure 3(a)" target="_self">Figure 3(a). Here we investigate the numerical dispersions are same for a specific wave speed c and it moves in the same direction
in Figure 3(a)" target="_self">Figure 3(a). Since the time step is the unconditionally stable in the scheme (4), so no longer restricted by the numerical constants, it is important and meaningful to see how a large time step impacts on numerical dispersion. Numerical dispersion f against t for different values of x shows in Figure 3(a)" target="_self">Figure 3(a). Here we investigate the numerical dispersions are same for a specific wave speed c and it moves in the same direction
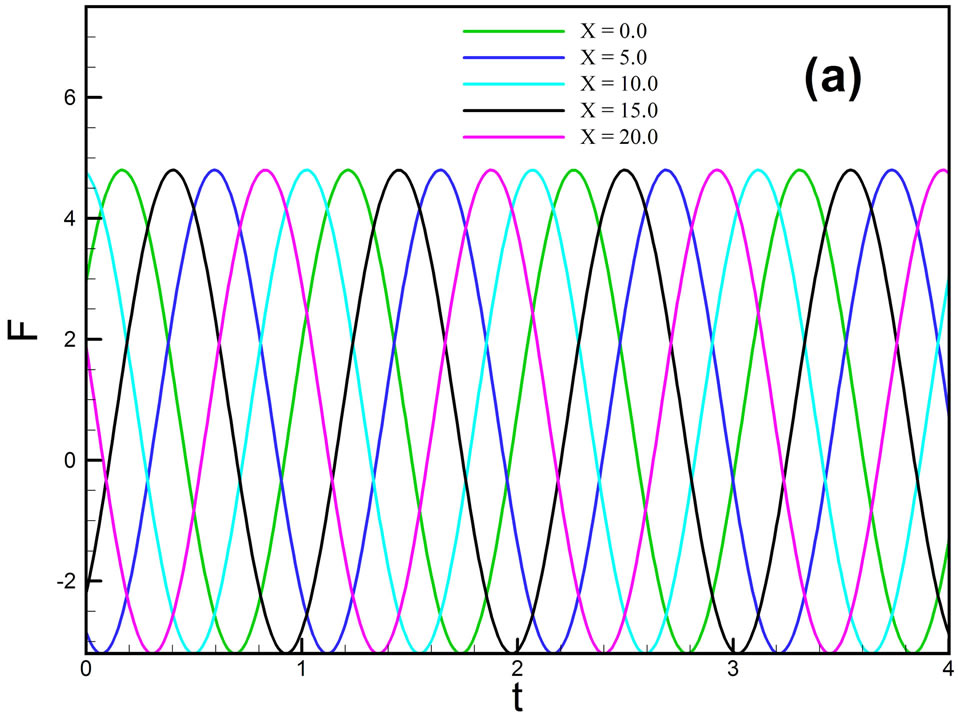

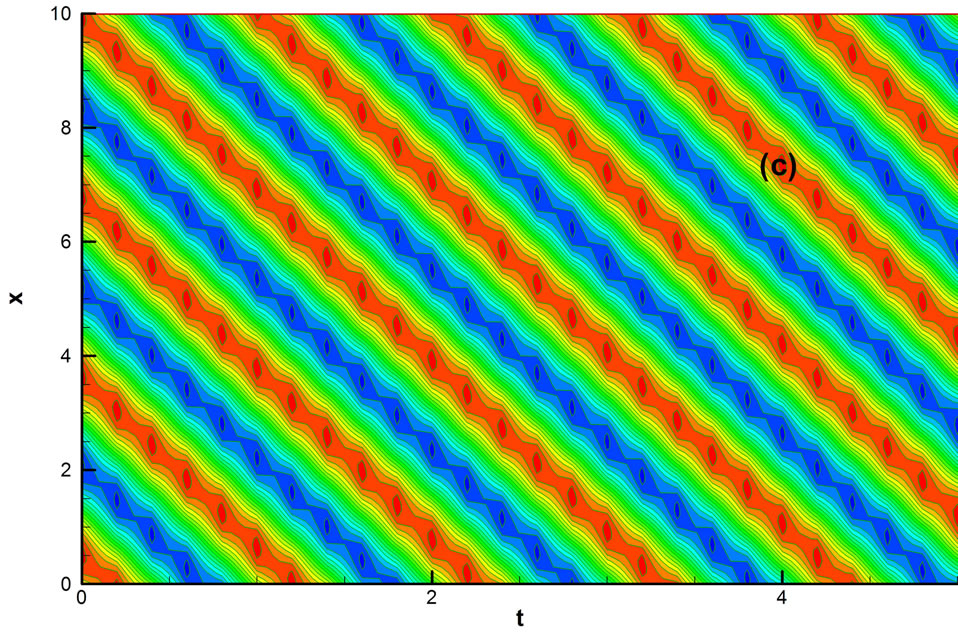
Figure 2. (a) Dispersion F against t for different values of x; (b) Dispersion F against x for different values of t; (c) Dispersion Contour of F against x and t.
against t for increasing values of x. Effect of the time step on dispersion relation shows in Figure 3(b)" target="_self">Figure 3(b) against x. It is very clear that for a particular wave speed c, the numerical dispersions are always same at every point for different moment and moves in the right direction against x for different time t. Numerical dispersion contour f against the position x and time t shows in Figure 3(c)" target="_self">Figure 3(c). For a particular wave against the position and time dis-


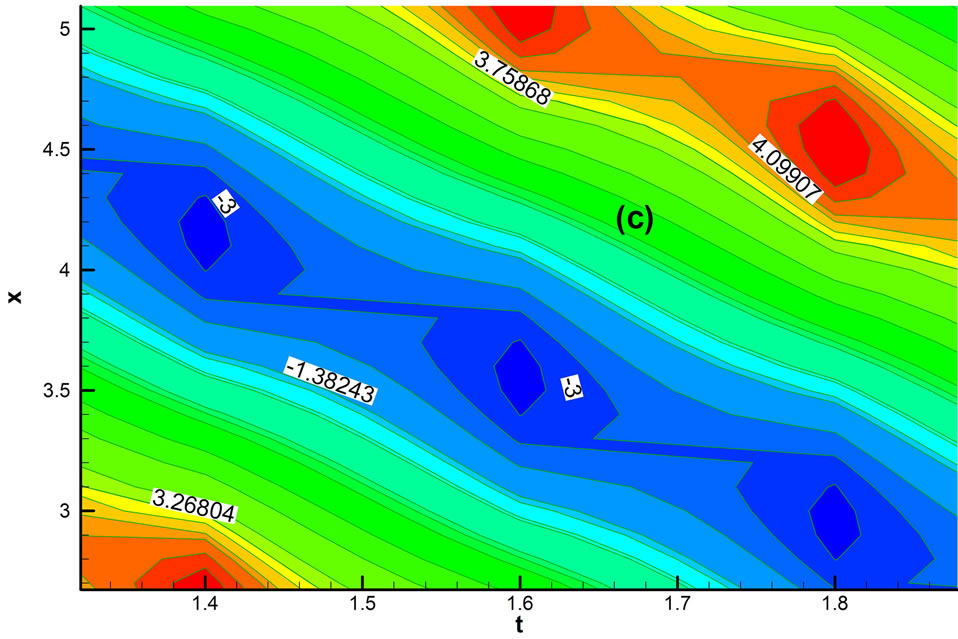
Figure 3. (a) Dispersion F against t for different values of x; (b) Dispersion F against x for different values of t; (c) Dispersion Contour of F against x and t.
persion contour are same. Here we see that dispersion contour is minimum −3.0 against x and t and it increases to a certain level and goes up to the maximum values of 4.09907.
Dispersion f plotted in Figure 4(a)" target="_self">Figure 4(a) with wave speed c = −5.0, numerical constants a = 4.0, D = 0.8 and . Dispersion relation f against t for different values of x is plotted in Figure 4(a)" target="_self">Figure 4(a). In order to view dispersion characteristics more closely and precisely, the dispersion relation of K-dV equation shown on cut of the (t, F) plane for positions x = 0.0, x = 5.0, x = 10.0, x = 15.0 and x = 20.0. At every position for a particular wave velocity c, dispersions are the same against t. Similarly, in Figure 4(b)" target="_self">Figure 4(b) we presents the numerical dispersion relation f against x for different values of t. Numerical dispersion f against x for different values of t like t = 0.1, t = 0.5, t = 0.9, t = 1.3 and t = 1.7 shows every moment for a
. Dispersion relation f against t for different values of x is plotted in Figure 4(a)" target="_self">Figure 4(a). In order to view dispersion characteristics more closely and precisely, the dispersion relation of K-dV equation shown on cut of the (t, F) plane for positions x = 0.0, x = 5.0, x = 10.0, x = 15.0 and x = 20.0. At every position for a particular wave velocity c, dispersions are the same against t. Similarly, in Figure 4(b)" target="_self">Figure 4(b) we presents the numerical dispersion relation f against x for different values of t. Numerical dispersion f against x for different values of t like t = 0.1, t = 0.5, t = 0.9, t = 1.3 and t = 1.7 shows every moment for a
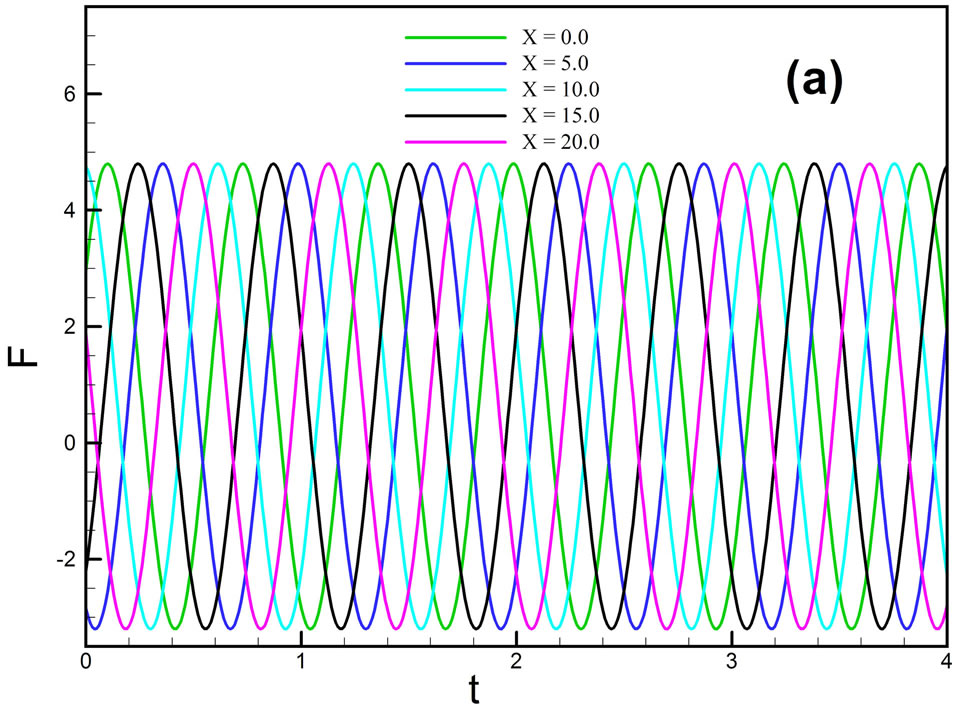
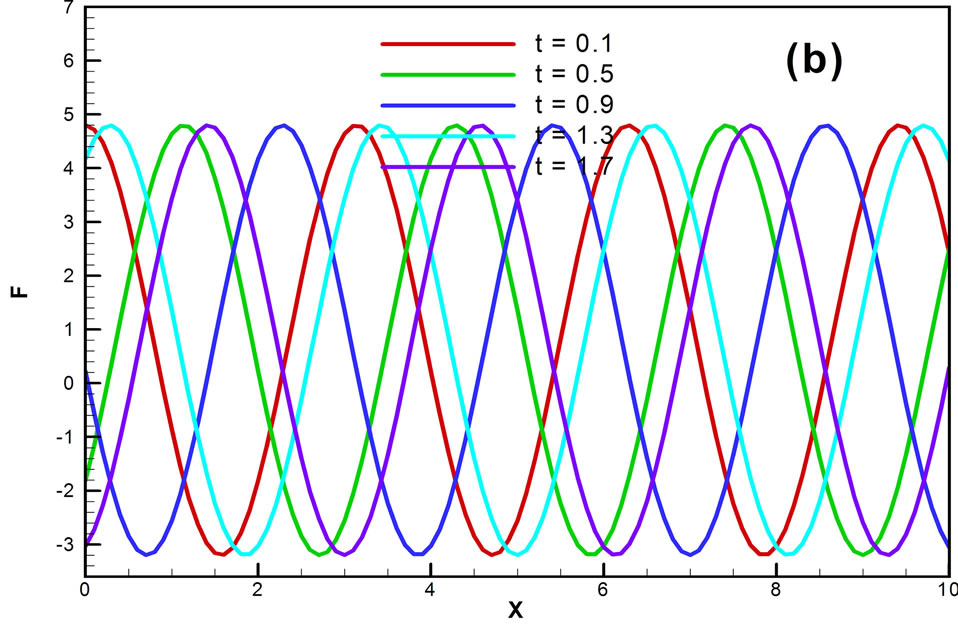
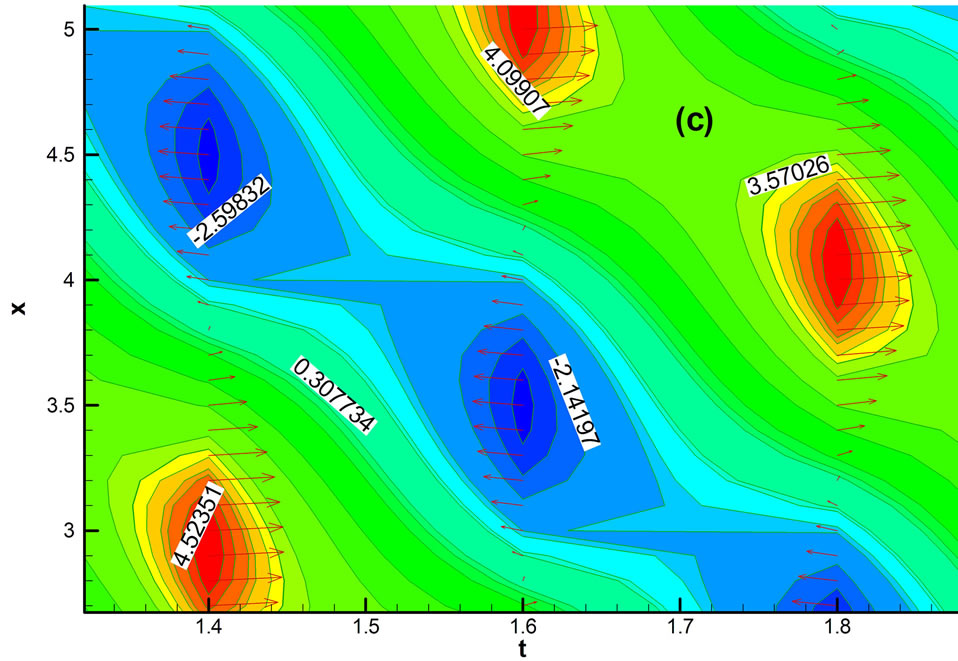
Figure 4. (a) Dispersion F against t for different values of x; (b) Dispersion F against x for different values of t; (c) Dispersion Contour of F against x and t.
specific travelling wave velocities are same at every position. In order to view dispersion characteristics more closely and precisely, the dispersion contour of f against space and time is shown in Figure 4(c). In Figure 4(c) for a particular wave, dispersive length is minimum and from the point wave moves both the direction. Similar analysis is there for dispersive height is maximum and from that point wave moves both the direction. For a particular wave the maximum dispersive length is 4.52351 and minimum is −2.14197 which shows in Figure 4(c).
Figures 5(a) to (c) presents our another interesting discovery. One can observe that the creation of a single dispersive “ripple” which moves to right against t in Figures 5(a) where wave speed c = −6.0, numerical constants a = 4.0, D = 0.8 and 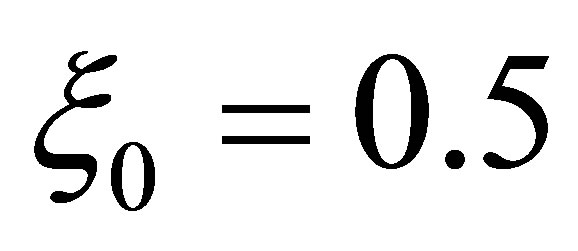 against t for different values of x like x = 0.0, x = 5.0, x = 10.0, x = 15.0 and x = 20.0. This phenomenon is almost same what we know about solutions of dispersive equations (K-dV). There, an infinite dispersive wave-train develops in time t for different values of x. It shows that the solution appears to strongly converge to the analytical solution of K-dV equation subject to the same initial speed of wave Dispersion relation f against x for different values of t shows in Figure 5(b), where wave speed c = −6.0, numerical constants a = 4.0, D = 0.8 and
against t for different values of x like x = 0.0, x = 5.0, x = 10.0, x = 15.0 and x = 20.0. This phenomenon is almost same what we know about solutions of dispersive equations (K-dV). There, an infinite dispersive wave-train develops in time t for different values of x. It shows that the solution appears to strongly converge to the analytical solution of K-dV equation subject to the same initial speed of wave Dispersion relation f against x for different values of t shows in Figure 5(b), where wave speed c = −6.0, numerical constants a = 4.0, D = 0.8 and . Dispersion f against x for different values of t are same for time t like t = 0.1, t = 0.5, t = 0.9, t = 1.3 and t = 1.7 moves in the right direction with same amplitude. In order to view dispersion characteristics more closely and precisely, the dispersion contour f against space and time are shown in Figure 5(c)" target="_self">Figure 5(c). In Figure 5(c)" target="_self">Figure 5(c) for a particular wave, dispersive length is minimum and from that point wave moves both the direction. Similar analysis are there dispersive height is maximum and from that point wave moves both the direction. For a particular wave the maximum dispersive length is 4.52351 and minimum is −2.14197 which shows in Figure 5(c)" target="_self">Figure 5(c). Dispersion against t for different values of x for controlling parameter a = 4.0, D = 0.8,
. Dispersion f against x for different values of t are same for time t like t = 0.1, t = 0.5, t = 0.9, t = 1.3 and t = 1.7 moves in the right direction with same amplitude. In order to view dispersion characteristics more closely and precisely, the dispersion contour f against space and time are shown in Figure 5(c)" target="_self">Figure 5(c). In Figure 5(c)" target="_self">Figure 5(c) for a particular wave, dispersive length is minimum and from that point wave moves both the direction. Similar analysis are there dispersive height is maximum and from that point wave moves both the direction. For a particular wave the maximum dispersive length is 4.52351 and minimum is −2.14197 which shows in Figure 5(c)" target="_self">Figure 5(c). Dispersion against t for different values of x for controlling parameter a = 4.0, D = 0.8, 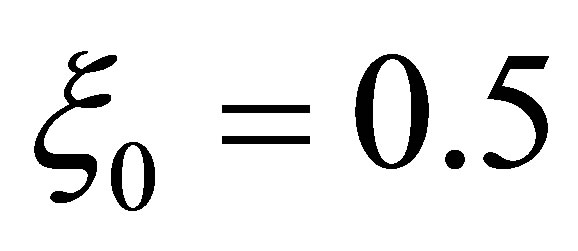 and
and 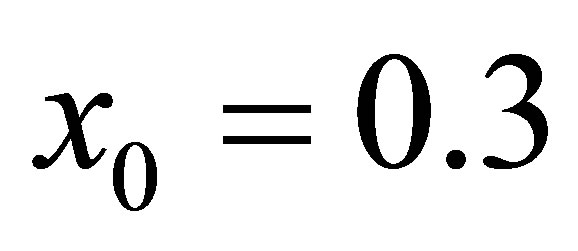 As seen in Table 1, in the initial stage (time t = 0.0) the dispersion of wave is maximum after that the wave gradually decreases and it diminishes with respect to time at x = 0.0. It is interesting that the dispersion of wave is steady state to the surface level at time t = 6.8 and it maintained up to t = 10.0. We observed that for x = 5.0 the dispersion wave is maximum at time t = 1.6 which is 8.966355. Dispersion wave is gradually increases from starting of the wave up to t = 1.6 after that it decreases gradually and diminishes at t = 8.8, it maintained up to t = 10.0. The dispersion wave is maximum at time t = 3.2 for x = 10.0 which is 8.966355. The behavior of the dispersion wave like as previous one. The maximum values of this dispersion for the both cases are 8.966355. Wave is gradually increases from starting of the wave up
As seen in Table 1, in the initial stage (time t = 0.0) the dispersion of wave is maximum after that the wave gradually decreases and it diminishes with respect to time at x = 0.0. It is interesting that the dispersion of wave is steady state to the surface level at time t = 6.8 and it maintained up to t = 10.0. We observed that for x = 5.0 the dispersion wave is maximum at time t = 1.6 which is 8.966355. Dispersion wave is gradually increases from starting of the wave up to t = 1.6 after that it decreases gradually and diminishes at t = 8.8, it maintained up to t = 10.0. The dispersion wave is maximum at time t = 3.2 for x = 10.0 which is 8.966355. The behavior of the dispersion wave like as previous one. The maximum values of this dispersion for the both cases are 8.966355. Wave is gradually increases from starting of the wave up


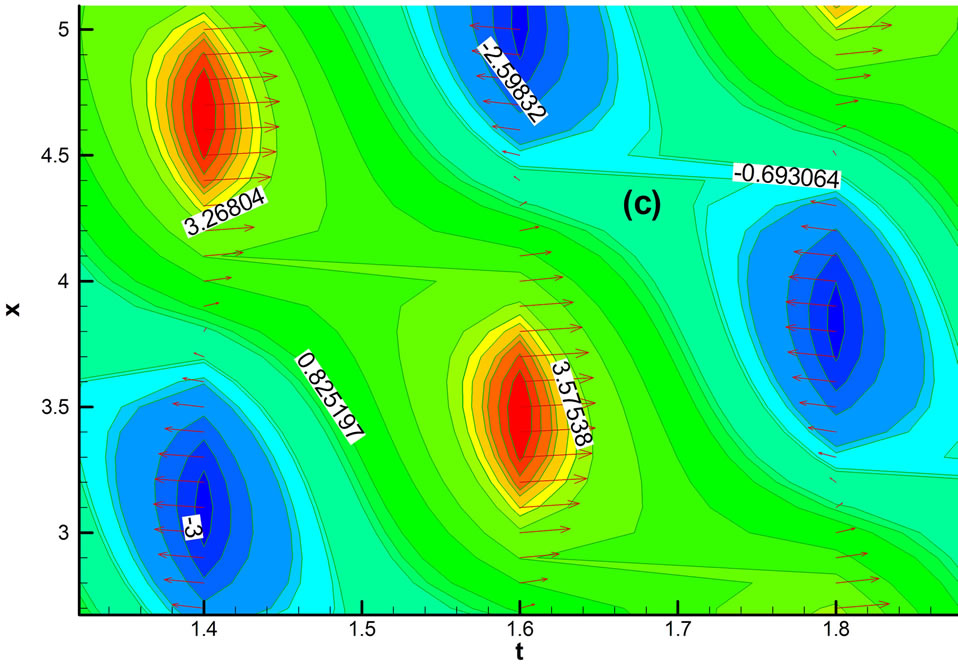
Figure 5. (a) Dispersion F against t for different values of x; (b) Dispersion F against x for different values of t; (c) Dispersion Contour of F against x and t.
to t = 3.2 after that it decreases gradually and diminishes at t = 10.0. We have got the maximum value two cases x = 5.0 and x = 10.0 of dispersion for two different time at t = 1.6 and t = 3.2 respectively. The interesting behavior of the dispersion wave provides the maximum values with respect to time for the different values of x, in that case the time difference maintaining arithmetically. Same analysis of the other cases like x = 15.0 and x = 20.0.
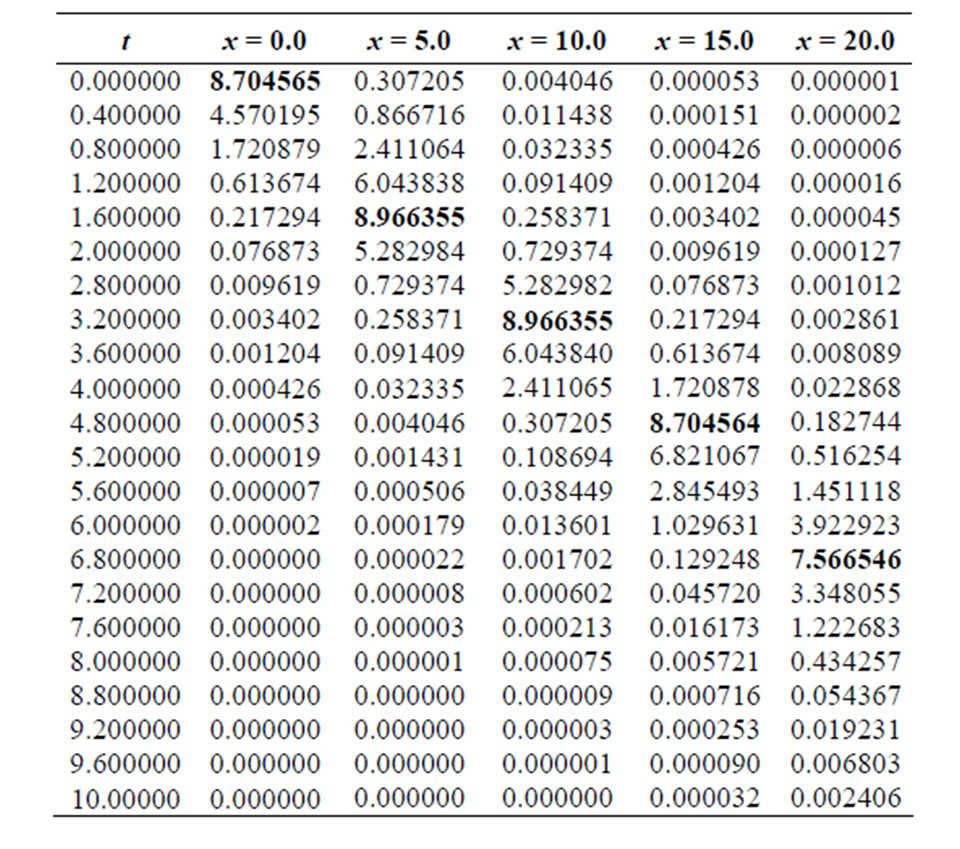
Table 1. Dispersion against t for different values of x for controlling parameter a = 4.0, D = 0.8, 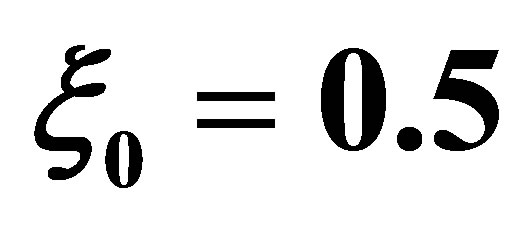 and x0 = 0.3.
and x0 = 0.3.
5. Conclusion
In this research, we have discussed the dispersion term analysis for K-dV equation being studied. Governing KdV equation for the present problem is third order and two-dimensional. It is found that (2) is a dispersive equation for the governing Equation (1). Using a new auxiliary equation method, we get new set of solution of the dispersive equation. It is found that exact dispersive solution (4) of two dimensional equations exists depending on relevant physical parameters. Numerical results of dispersive term for K-dV equation obtained by FORTRAN program have been shown graphically and discussed. We have also found that when employing FortranScheme for the numerical estimation of K-dV equation, it presents graphically for different speed of water wave. Different speed of water makes the different physical interpretation of dispersive term that is clearly shown in our result and discussion section. Non-linear phenomena have the real physical interpretation. There are lots of scopes to investigate different types of higher order nonlinear partial differential equation from the ideas of our method.
REFERENCES
- M. Ablowitz and H. Segur, “Solitons and the Inverse Scattering Transform,” SIAM, Philadelpha, 1981. http://dx.doi.org/10.1137/1.9781611970883
- L. Debnath, “Nonlinear Partial Differential Equations: For Scientists and Engineers,” 2nd Edition, Birkhöuser, Boston, 2005. http://dx.doi.org/10.1007/b138648
- J. Dorea and A. Huerta, “Finite Element Method for Flow Problems,” John Wiley & Sons Ltd., New York, 2003.
- R. W. Lewis, R. W. Nithiarasu and P. Seethanamu, “Fundamentals of the Finite Element Method for Heat and Fluid Flow,” John Wiley & Sons, Inc., New York, 2004. http://dx.doi.org/10.1002/0470014164
- A. Biswas and S. Konar, “Soliton Perturbation Theory for the Compound K-dV Equation,” International Journal of Theoretical Physics, Vol. 46, No. 2, 2007, pp. 237-243. http://dx.doi.org/10.1007/s10773-006-9231-z
- F. G. Drazin and R. S. Johnson, “Solitons: An Introduction,” 2nd Edition, Cambridge University Press, New York, 1989. http://dx.doi.org/10.1017/CBO9781139172059
- H. Segur “The Korteweg-de Vries Equations and Water Waves Solutions of the Equation, Part I,” Journal of Fluid Mechanics, Vol. 59, No. 4, 1973, pp. 721-736. http://dx.doi.org/10.1017/S0022112073001813
- J. L. Hammack and H. Segur, “The Korteweg-de Vries Equation and Water Waves, II. Comparison with Experiments,” Journal of Fluid Mechanics, Vol. 65, No. 2, 1974, pp. 289-313. http://dx.doi.org/10.1017/S002211207400139X
- J. L. Hammack and H. Segur, “The Korteweg-de Vries Equation and Water Waves, III. Oscillatory Waves,” Journal of Fluid Mechanics, Vol. 84, No. 2, 1978, pp. 337-358. http://dx.doi.org/10.1017/S0022112078000208
- T. Trogdon, S. Olver and B. Deconninck “Numerical Inverse Scattering for the Korteweg-de Vries and Modified Korteweg-de Vries Equations,” Physica D, Vol. 241, 2012, pp. 1003-1025.
- G. Whitham, “Linear and Nonlinear Waves,” Wiley-Interscience, New York, 1974.
- P. Le Blond and L. Mysak, “Waves in the Ocean,” El- - sevier, Amsterdam, 1978.
- D. Korteweg and G. de-Vries, “On the Change of Form of Long Waves Advancing in a Rectangular Canal, and on a New Type of Long Stationary Waves,” Philosophical Magazine, Vol. 39, No. 240, 1895, pp. 422-443. http://dx.doi.org/10.1080/14786449508620739
- J. Boussinesq, “Theorie de I’intumescence Liquid, Appleteonde Solitaire au de Translation, se Propageantdansun Canal Rectangulaire,” Les Comptes Rendus de l'Académie des Sciences, Vol. 72, 1871, pp. 755-759.
- J. Boussinesq, “Thorie des Ondes et Des Remous Qui se Propagent le Long d’un Canal Rectangulaire Horizontal, en Communiquant au Liquidecontenudansce Canal des Uitessessensiblementpareilles de la Surface au Fond”, Journal de Mathématiques Pures et Appliquées, Vol. 17, 1872, pp. 55-108.
- D. Peregrine “Long Waves on a Beach,” Journal of Fluid Mechanics, Vol. 27, 1967, pp. 815-827. http://dx.doi.org/10.1017/S0022112067002605
- D. Burwell, E. Tolkova and A. Chawla, “Diffusion and Dispersion Characterization of a Numerical Tsunami Model,” Ocean Modelling, Vol. 19, No. 1-2, 2007, pp. 10-30. http://dx.doi.org/10.1016/j.ocemod.2007.05.003
- G. Schroeder and K. Schlǘnzen, “Numerical Dispersion of Gravity Waves,” Monthly Weather Review, Vol. 137, No. 12, 2009, pp. 4344-4354. http://dx.doi.org/10.1175/2009MWR2890.1

