American Journal of Computational Mathematics
Vol.3 No.1(2013), Article ID:29147,2 pages DOI:10.4236/ajcm.2013.31009
Primality Test
Via Cornelia, Rome, Italy
Email: martino.gabri@gmail.com
Received October 12, 2012; revised November 27, 2012; accepted December 5, 2012
Keywords: Prime Numbers; Equation
ABSTRACT
In this paper we will give an algorithm that in the worst case solve the question about the primality of a number in 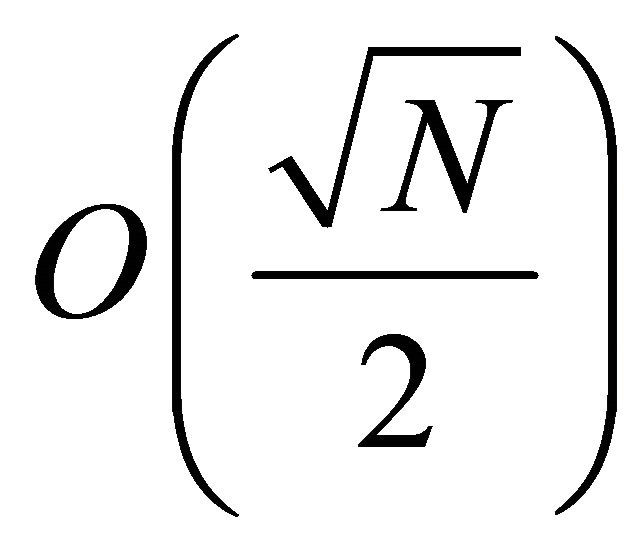 but that gives better result if the number is not prime (constant operation). Firstly, we will introduce an equation on which are based not prime numbers. With this equation it is possible to deduce the prime number that generates a not prime number and to establish an equation in which if exists a certain integer the number is not prime and therefore vice versa to deduce if it is prime.
but that gives better result if the number is not prime (constant operation). Firstly, we will introduce an equation on which are based not prime numbers. With this equation it is possible to deduce the prime number that generates a not prime number and to establish an equation in which if exists a certain integer the number is not prime and therefore vice versa to deduce if it is prime.
1. Introduction
There exist different primality test [1,2]. The most simple is to check all the divisors of a given number N. If the number has some divisor with remainder 0, then the number is not prime. Another method uses the Wilson Theorem, but it is quiets inefficient. Some methods certificate the primality with some probability. Those methods can assure certify always if a number is prime and in some case certify than a number is prime even if it is not. Those methods take a value a from a set previously calculated. One example is the Miller Rabin Test. Given a number n, we choose a number a and state the even number 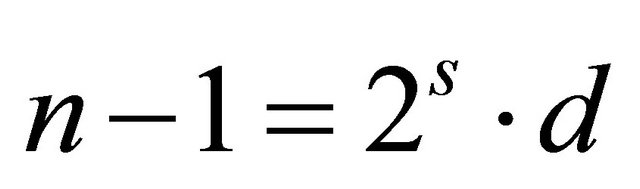 with s positive integer and d positive odd integer. If
with s positive integer and d positive odd integer. If 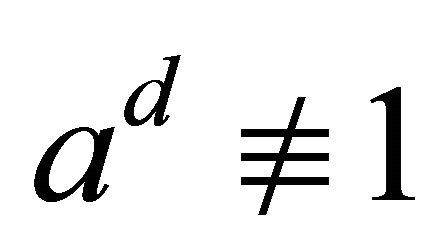 (mod n) and
(mod n) and 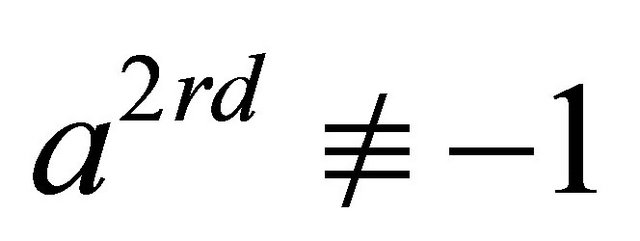 (mod n) the number is composite. As deterministic, the most successful algorithm is the Manindra Agrawal, Neeraj Kayal, and Nitin Saxena Test [3]. The algorithm is based on the equation
(mod n) the number is composite. As deterministic, the most successful algorithm is the Manindra Agrawal, Neeraj Kayal, and Nitin Saxena Test [3]. The algorithm is based on the equation 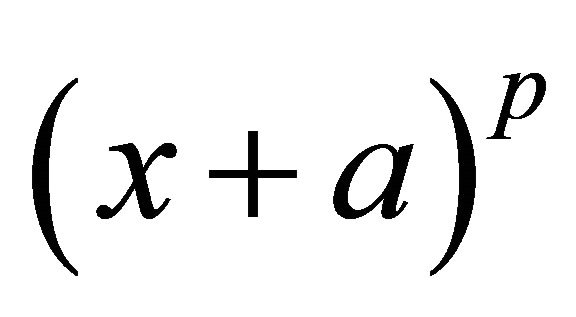 mod
mod 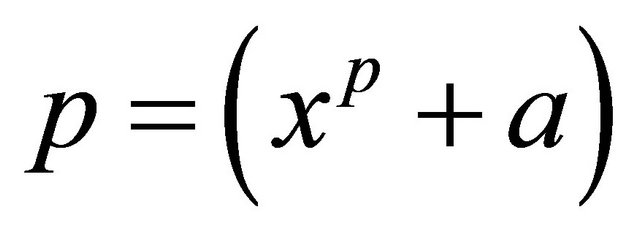 mod p for a, p prime and for each x. They were able to reasonably speed up the expansion of the binomial terms. To do this they state that the formula is valid also for the polynomial divided by
mod p for a, p prime and for each x. They were able to reasonably speed up the expansion of the binomial terms. To do this they state that the formula is valid also for the polynomial divided by 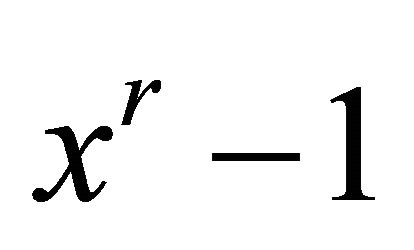 with r small prime:
with r small prime: 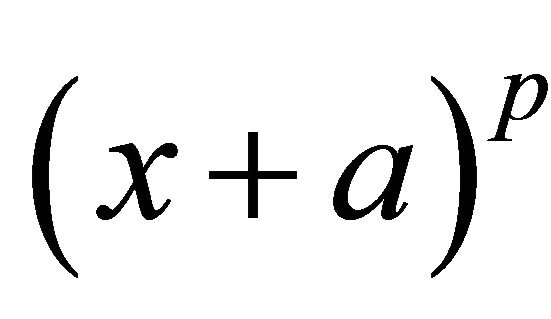 mod
mod 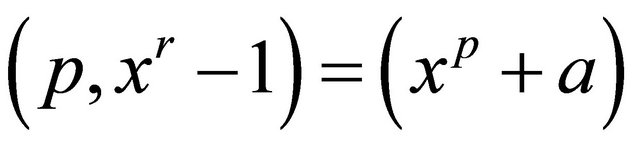 mod
mod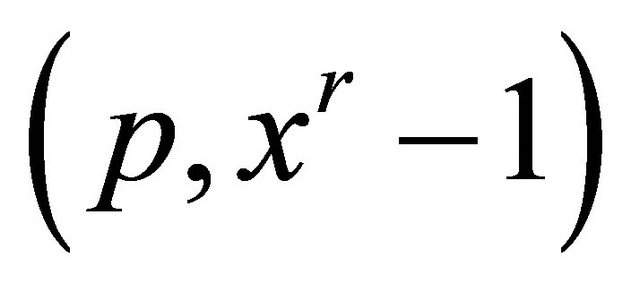 . In this way the remainder has only r + 1 terms.
. In this way the remainder has only r + 1 terms.
An Equation for Not Prime
The algorithm is based on the fact that a number is not prime when is even or when it has a form of the kind 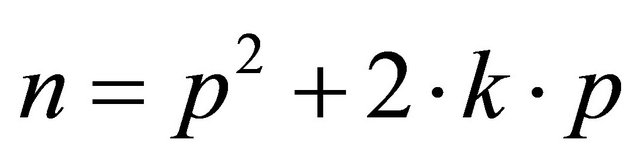 where n is the generated number, p is an integer prime
where n is the generated number, p is an integer prime 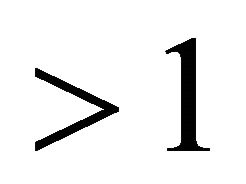 and
and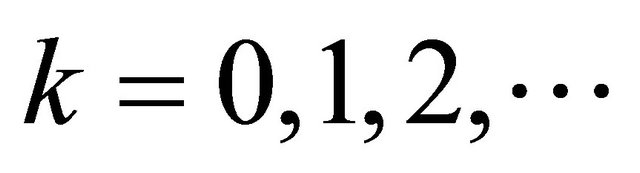 . Therefore it is necessary to solve the equation
. Therefore it is necessary to solve the equation
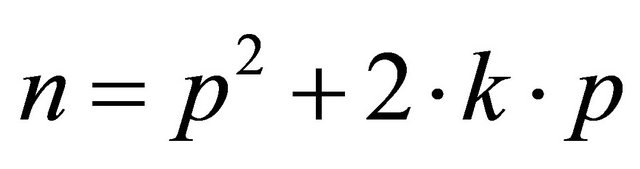 (1)
(1)
with variable p that gives the positive solution
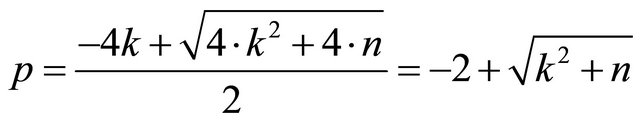 (2)
(2)
In general we have
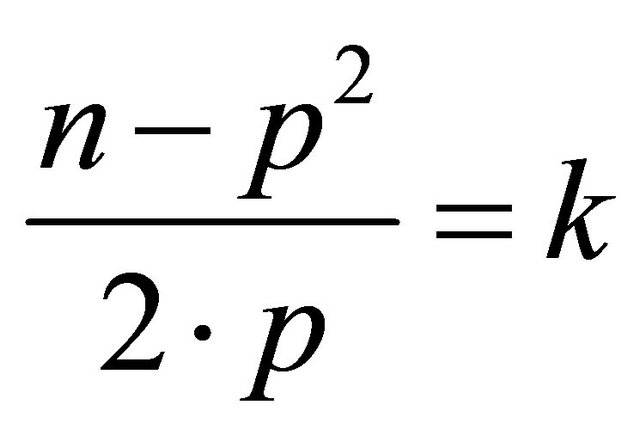 (3)
(3)
If k is an integer for a certain prime the number is generated. The set of primes is in the set of odds. If a condition is valid for the odds we can assert that it is valid for the prime and therefore if k is integer for an odd number is integer for a prime and therefore the number is generated.
2. Method
It is based on statement (3)
number isprime isprime = true if number mod 2 == 0 then isprime = false
end if
for odd = 3, 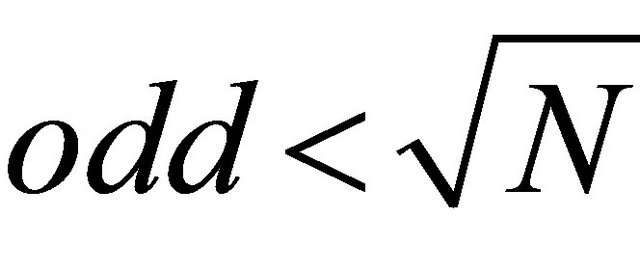 And
And , odd = odd + 2 if
, odd = odd + 2 if 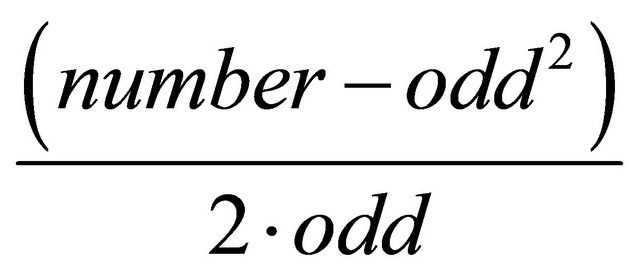 integer then isprime = false
integer then isprime = false
end if
end for
return isprime.
3. Computational Complexity
The method requires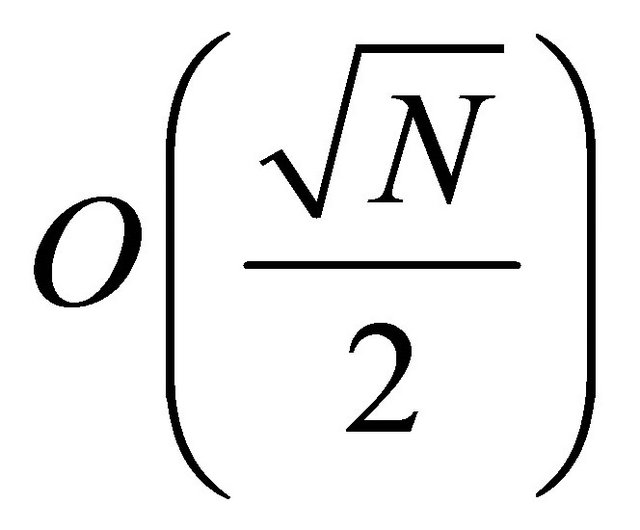 .
.
4. Results
The test has been done with
• Asus notebook
• Intel i7 processor
• 4 GB Ram
• Java Programming Language
• Windows 7 OS For the number 99999989 that is prime the result is run: true BUILD SUCCESSFUL (total time: 0 seconds).
Not counted by the machine as significative.
5. Discussion
If we apply L’Hopital’s rule [4] for the asymptotic analysis with 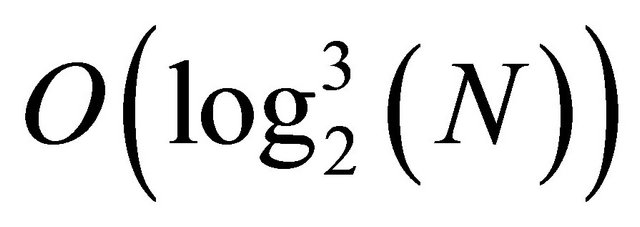 as confront term. We obtain derivative ratio
as confront term. We obtain derivative ratio
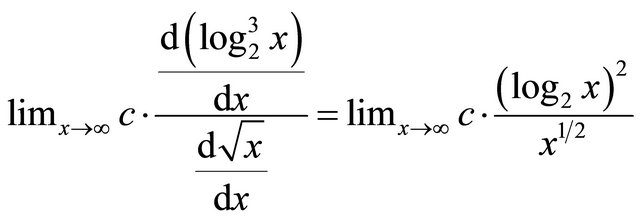 where c is a constant value, so applying again L’Hopital’s rule the ratio became
where c is a constant value, so applying again L’Hopital’s rule the ratio became 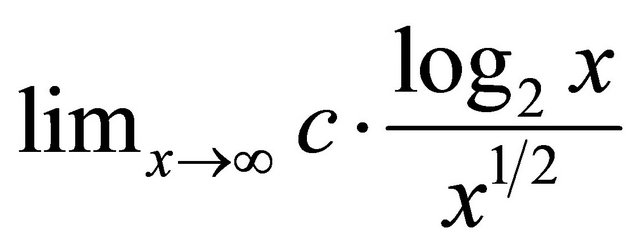 and applying again
and applying again 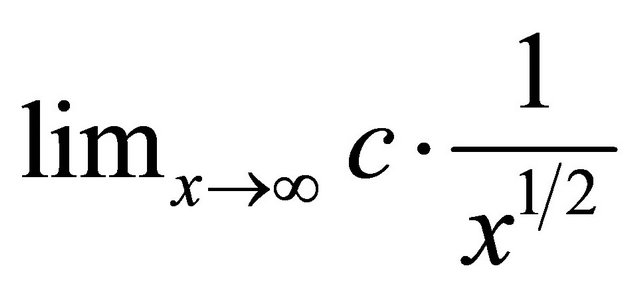 that goes to zero for x that goes to infinity. The result is not asymptotically better than
that goes to zero for x that goes to infinity. The result is not asymptotically better than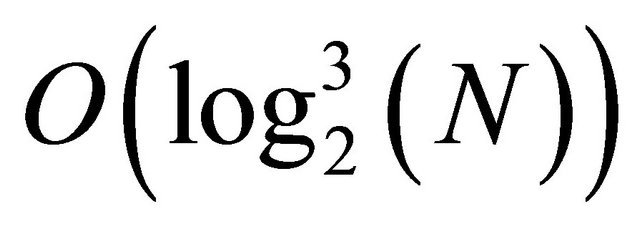 , if we estimate the plot of the two functions we reach the asymptotic cross-over after the interval [2, 192823208].
, if we estimate the plot of the two functions we reach the asymptotic cross-over after the interval [2, 192823208].
REFERENCES
- S. Aaronson, “The Prime Facts: From Euclid to AKS,” Lecture Notes, 2003.
- Wikipedia. http://en.wikipedia.org/wiki/Primality_test
- Wikipedia. http://en.wikipedia.org/wiki/AKS_primality_test
- Wikipedia. http://en.wikipedia.org/wiki/L'Hopital's Rule

