American Journal of Computational Mathematics
Vol.2 No.3(2012), Article ID:23204,7 pages DOI:10.4236/ajcm.2012.23030
Recent Modifications of Adomian Decomposition Method for Initial Value Problem in Ordinary Differential Equations
Department of Mathematics, Science Faculty for Girls, King Abdulaziz University, Jeddah, KSA
Email: malmazmumy@kau.edu.sa, falhendi@kau.edu.sa, hbakodah@kau.edu.sa, hzalzumi@kau.edu.sa
Received May 12, 2012; revised June 20, 2012; accepted July 1, 2012
Keywords: Adomian Decomposition Method; Initial Value Problem; Modified Adomian Decomposition Method
ABSTRACT
In this paper, some modifications of Adomian decomposition method are presented for solving initial value problems in ordinary differential equations. Also, the restarted and two-step methods are applied to the problem. The effectiveness of the each modified is verified by several examples.
1. Introduction
Recently a great deal of interest has been focused on the application of Adomian’s decomposition method to solve a wide variety of linear and nonlinear problems [1]. This method generates a solution in the form of a series whose terms are determined by a recursive relationship using the Adomian polynomials. Researchers who have used the ADM have frequently enumerated on the many advantages that it offers. Since it was first presented in the 1980’s, Adomian decomposition method has led to several modifications on the method made by various researchers in an attempt to improve the accuracy or expand the application of the original method. Adomian and Rach [2] introduced modified Adomian polynomials which converge slightly faster than the original polynomials and are convenient for computer generation. Adomian also introduced accelerated Adomian polynomials [3], despite the various types of Adomian polynomials available, the original Adomian polynomials are more generally used based on the advantage of a convenient algorithm which is easily remembered. Recently, F. A. Hendi et al. [4] presented simple Mathematica program to compute Adomian polynomials. Wazwaz [5] used padé approximants to the solution obtained using a modified decomposition method and found that not only does this improve the result, but also that the error decreases with the increase of the degree of the padé approximants. Another modification to ADM was proposed by Wazwaz [6] a reliable modification of the Adomian decomposition method. In 2005, Wazwaz [7] presented another type of modification to the ADM. New modification was proposed by Luo [8,9], this variation separates the ADM into two steps and therefore is termed the two-step ADM or ( TS ADM ). Another recent modification is termed the restarted Adomian method [10,11], this method involves repeatedly updating the initial term of the series generated.
Several other researchers have developed modifications to the ADM [12-17]. The modifications arise from evaluating difficulties specific for the type of problem under consideration. The modification usually involves only a slight change and is aimed at improving the convergence or accuracy of the series solution. The main goal of this paper is to apply some modifications of Adomian decomposition method to the initial value problem in ordinary differential equation and compare the results of an original ADM to those with the modifications. As we know, we point out that restarted and two-step methods are applied on the initial value problem for the first time. Our numerical examples show which of these methods give best results.
2. A General Description of the ADM
A general nonlinear differential equation will be used for simplicity, we consider
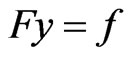
where F is a nonlinear differential operator and y and f are functions of x. Rewriting the equation in the operator form
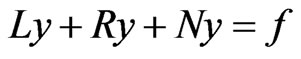 (1)
(1)
where L is an operator representing the linear portion of F which easily invertible, R is a linear operator for the reminder of the linear portion, and N is a nonlinear operator representing the nonlinear term in F.
Applying the inverse operator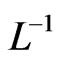 , the equation then becomes
, the equation then becomes
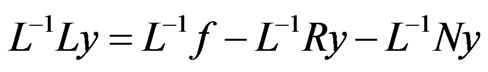
since F was taken to be a differential operator and L is linear,  would represents an integration and with any given initial conditions,
would represents an integration and with any given initial conditions, 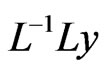 will give an equation for y incorporating these conditions. This gives
will give an equation for y incorporating these conditions. This gives
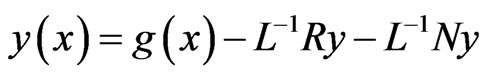 (2)
(2)
where  represents the function generated by integrating f and using the initial conditions.
represents the function generated by integrating f and using the initial conditions.
Adomian decomposition method admits the decomposition into an infinite series of components
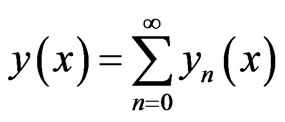 (3)
(3)
The nonlinear term 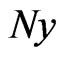 be equated to an infinite series polynomial
be equated to an infinite series polynomial
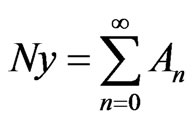 (4)
(4)
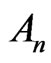 is the Adomian polynomials, which can be determined by
is the Adomian polynomials, which can be determined by
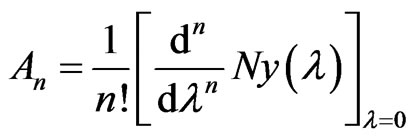 (5)
(5)
substituting (4) and (5) into (2)
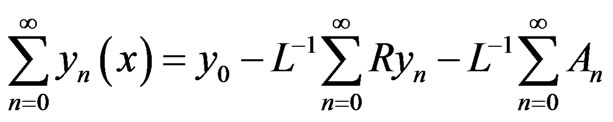
the recursive relationship is found to be
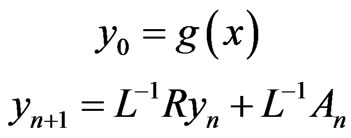 (6)
(6)
Having determined the components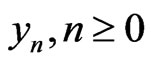 , the solution y in a series form follows immediately. The series may be summed to provide the solution in a closed form. However, for concrete problems, the n-term partial sum may be used to give the approximate solution.
, the solution y in a series form follows immediately. The series may be summed to provide the solution in a closed form. However, for concrete problems, the n-term partial sum may be used to give the approximate solution.
2.1. Convergence Analysis
The concept of convergence of the solution obtained by Adomian decomposition method was addressed by [1,18], and extensively by [19,20]. Convergence of the ADM when applied to initial value problem in ordinary differential equation is discussed by many authors. For example, K. Abbaoui and Y. Cherruault [21,22]. In [23] H. Alzumi et al. discussed the convergence of ADM.
2.2. The Noise Terms Phenomenon
In this section, we will present a useful tool that will accelerate the convergence of the Adomian decomposition method. The noise terms phenomenon provides a major advantage in that it demonstrate a fast convergence of the solution. A useful summary about the noise terms phenomenon can be drawn as follows:
• The noise terms are defined as the identical terms with opposite signs that may appear in the components  and
and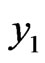 .
.
• The noise terms appear only for specific types of inhomogeneous equations whereas noise terms do not appear for homogeneous equations.
• Noise terms may appear if the exact solution is part of the zeroth component .
.
• Verification that the remaining non-canceled terms satisfy the equation is necessary and essential.
For further reading about the noise terms phenomenon see [24-27].
3. Some Recent Modifications of ADM
Several authors have proposed a variety of modifications to ADM. The modifications arise from evaluating difficulties specific for the type of problem under consideration. We begin with the Adomian’s modification.
3.1. Modified Adomian Method (M1): [1,28]
Power series solutions of linear homogeneous differential equation in initial-value problems yield simple recurrence relations for the coefficient, but they are generally not adequate for nonlinear equations, although applicable to some simple cases such as the Riccati equation. To clarify the procedure, consider the general inhomogeneous nonlinear form (1), where L will be chosen as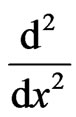 , and operate with
, and operate with  We now have
We now have
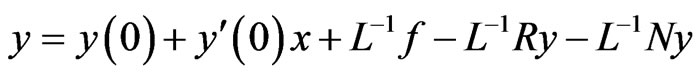 (7)
(7)
Let
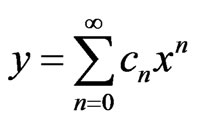 ,
, 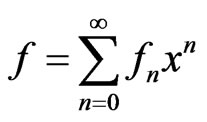 , and
, and 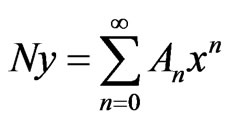 (8)
(8)
Now from (8) in (7), we obtain
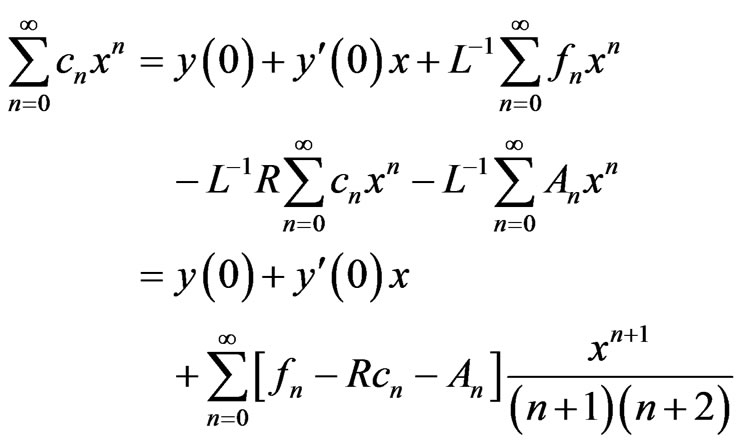
or
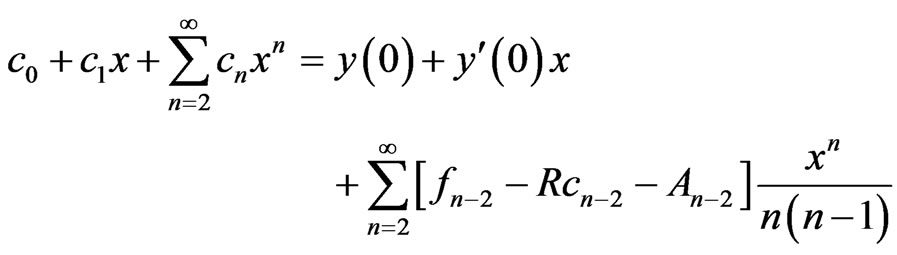
Equating coefficients, leading to:
 (9)
(9)
where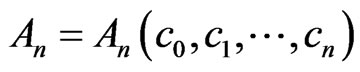 .
.
3.2. Wazwaz Modifications
3.2.1. Reliable Modification (M2): [6,29]
The reliable modification form based on the assumption that the function g in (2) can be divided into two parts, i.e.
 (10)
(10)
Accordingly, a slight variation was proposed only on the components  and
and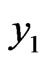 . The suggestion was that only the parts
. The suggestion was that only the parts  be assigned to the component
be assigned to the component , whereas the remaining part
, whereas the remaining part 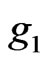 be combined with other terms given in (6) to define
be combined with other terms given in (6) to define . Consequently, the recursive relation,
. Consequently, the recursive relation,
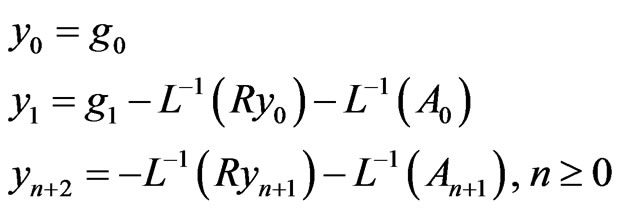 (11)
(11)
Although this variation in the formation of 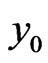 and
and  is slight, however it plays a major role in accelerating the convergence of the solution and in minimizing the size of calculations.
is slight, however it plays a major role in accelerating the convergence of the solution and in minimizing the size of calculations.
Furthermore, there is no need sometimes to evaluate the so-called Adomian polynomials required for nonlinear operators. Two important remarks related to the modified method were made in [6]. First, by proper selection of the function 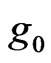 and
and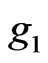 , the exact solution y may be obtained by using very few iterations, and sometimes by evaluating only two components. The success of this modification depends only on the choice of
, the exact solution y may be obtained by using very few iterations, and sometimes by evaluating only two components. The success of this modification depends only on the choice of  and
and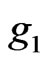 , and this can be made through trials, that are the only criteria which can be applied so far.
, and this can be made through trials, that are the only criteria which can be applied so far.
Second, if g consists of one term only, the standard decomposition method should be employed in this case.
3.2.2. The New Modification (M3): [30]
As indicated earlier, although the modified decomposition method may provide the exact solution by using two iterations only, and sometimes without any need for Adomian polynomials, but its effectiveness depends on the proper choice of  and
and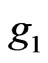 . In the new modification, Wazwaz replaces the process of dividing g into two components by a series of infinite components. He suggests that g be expressed in Taylor series
. In the new modification, Wazwaz replaces the process of dividing g into two components by a series of infinite components. He suggests that g be expressed in Taylor series
 (12)
(12)
Moreover, he suggest a new recursive relationship expressed in the form
 (13)
(13)
It is important to note that if g consists of one term only, then scheme (13) reduces to relation (6). Moreover, if g consists of two terms, then relation (13) reduces to the modified relation (11). It is easily observed that algorithm (13) reduces the number of terms involved in each component, and hence the size of calculations is minimized compared to the standard Adomian decomposition method only. Moreover, this reduction of terms in each component facilitates the construction of Adomian polynomials for nonlinear operators.
3.3. Restarted Adomian Method (M4): [10,11]
The restarted ADM was used in [10] as a new method based on standard ADM for solving algebraic equations. In [11], E. Babolian et al. applied the restarted Adomian method to nonlinear integral equations and nonlinear integro-differential equations. The author in [31] applied the method to solve a system of nonlinear Fredholm integral equations of the second kind.
In this method, we use the modified Adomian method which proposed a slight variation only on the components 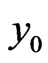 and
and , and restarted Adomian method applied to algebraic equations. The rate of the method is more accelerate than standard adomian method. If we consider a general nonlinear equation of the form (1) and applied ADM to solve it we get the recursive relationship (6), we introduce the algorithm of restarted Adomian method as the following:
, and restarted Adomian method applied to algebraic equations. The rate of the method is more accelerate than standard adomian method. If we consider a general nonlinear equation of the form (1) and applied ADM to solve it we get the recursive relationship (6), we introduce the algorithm of restarted Adomian method as the following:
Choose small natural numbers .
.
Apply the Adomian method on Equations (6) and calculate 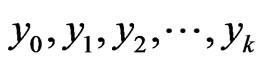
Set 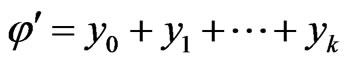
Let Z be the proper function which will be determined next for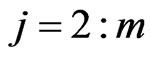 ,
, 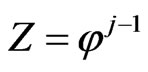

• Remarks:
• 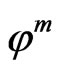 can be considered as an approximation of (1).
can be considered as an approximation of (1).
• The Adomian method usually gives sum of the some first terms as an approximation of y, in this algorithm we can update  in each step, but we don’t calculate the terms with large index, so m and k are considered small.
in each step, but we don’t calculate the terms with large index, so m and k are considered small.
3.4. Two-Step Adomian Method (M5): [8,9]
The Two-step Adomian decomposition method (TSADM) is derived by separate the standard ADM into two steps. The main ideas of two-step Adomian decomposition method for the differential Equation (1), are:
Applying the inverse operator  to f, and using the given conditions, we obtain
to f, and using the given conditions, we obtain
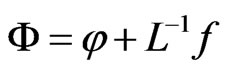
where the function  represents the terms arising from using the given conditions, all are assumed to be prescribed.
represents the terms arising from using the given conditions, all are assumed to be prescribed.
To achieve the objectives of this study, we set

Based on this, we define

where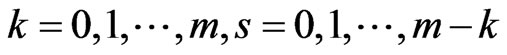 .
.
Then, we verify that 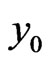 satisfies the original equation and the given conditions by substitution, once the exact solution is obtained we finish. Otherwise, we go to the following step two.
satisfies the original equation and the given conditions by substitution, once the exact solution is obtained we finish. Otherwise, we go to the following step two.
We set 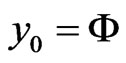 and continue with the standard Adomian recursive relation
and continue with the standard Adomian recursive relation
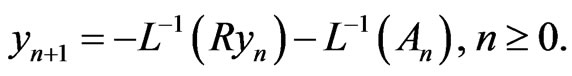
Compared to the standard Adomian method and the modified method, we can see that the two-step Adomian method may provide the solution by using one iteration only. Further, the (TSADM) avoids the difficulties arising in the modified method. Furthermore, the number of the terms in 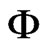 namely m, is small in many practical problems.
namely m, is small in many practical problems.
4. Numerical Examples
In this section, some initial value problems are considered to show the efficiency of each modified.
Example 1
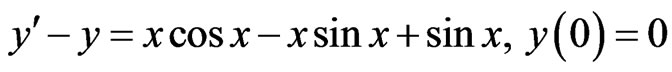
MS (Standard Adomian Method):
Applying 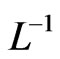 to both sides yields
to both sides yields
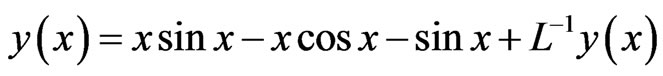
The recursive relationship
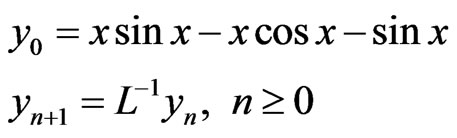
So

Other components can be evaluated in a similar manner. It is easily observed that the noise terms 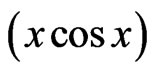 and
and  appear in
appear in 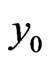 and
and 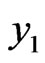 with opposite signs. Canceling these noise terms from
with opposite signs. Canceling these noise terms from 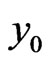 gives the exact solution
gives the exact solution  that can be justified through substitution. It is worth noting that other noise terms that appear in other components vanish in the limit.
that can be justified through substitution. It is worth noting that other noise terms that appear in other components vanish in the limit.
M1: Let
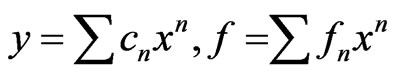
Then
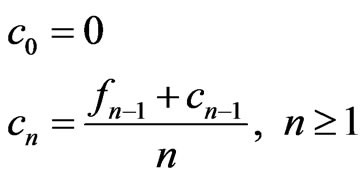
So that
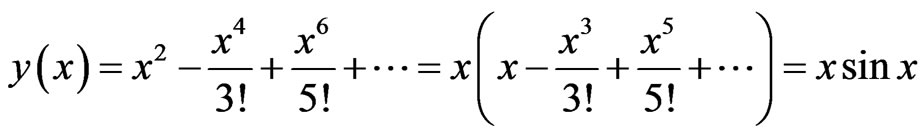
M2:
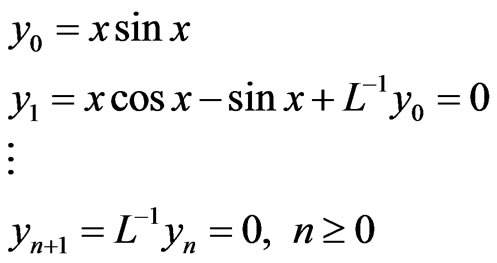
Then the exact solution is 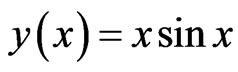
M3: The Taylor expansion for  is given by
is given by
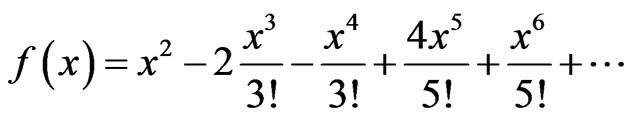
Then the recursive relationship
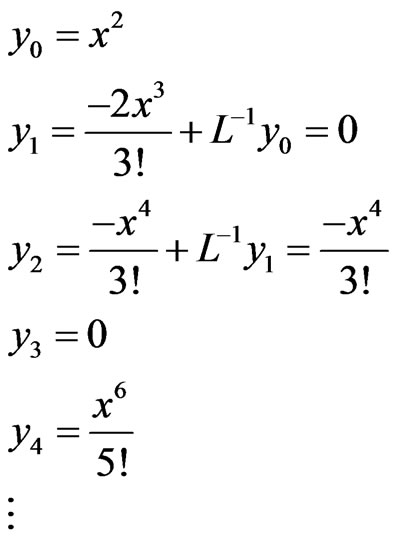
The solution in a series form is given by
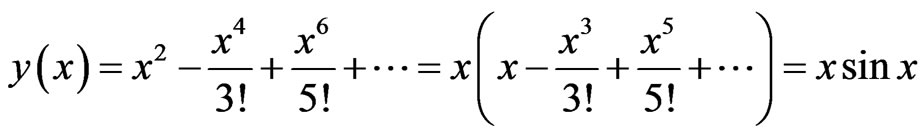
M4: Let
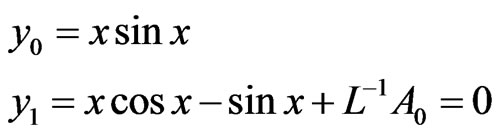
Then
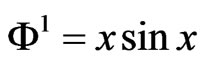
Then the exact solution is .
.
M5: Let
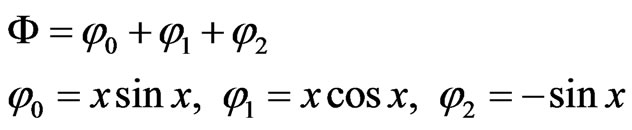
Clearly 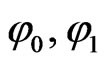 and
and 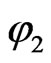 satisfy
satisfy , by selecting
, by selecting 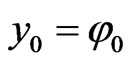 and by verifying that
and by verifying that 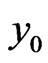 justified the differential equation.
justified the differential equation.
Then, the exact solution is obtained immediately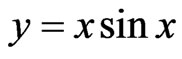 .
.
Example 2
Consider nonlinear initial value problem
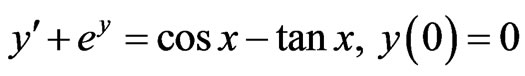
With the exact solution .
.
Ms:
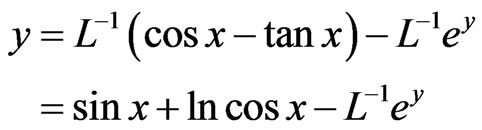
 is Adomian polynomials of nonlinear term
is Adomian polynomials of nonlinear term 
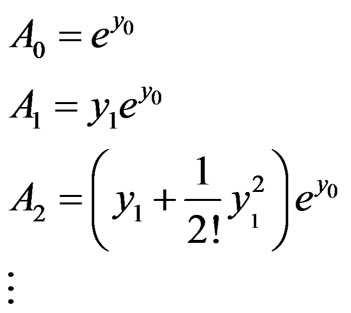
with standard ADM, we obtained the recursive relationship

It is easy to see that the standard Adomian decomposition method converges to the exact solution very slowly, comparison of absolute errors between the exact solution and approximate solutions Ms introduce in Table 1 and Figure 1.
M1: Let
Then
So
From this relation we get
This yield

So the  coefficients
coefficients
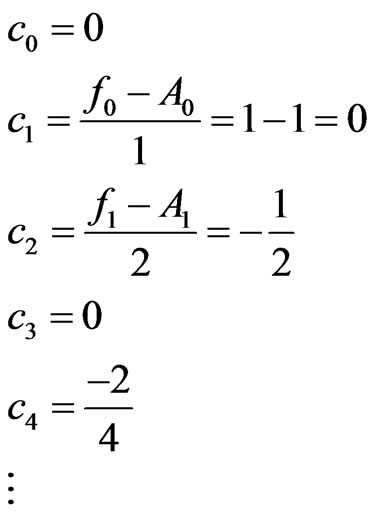
The series solution 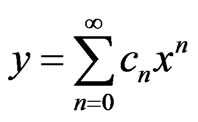 obtained as
obtained as 
M2: 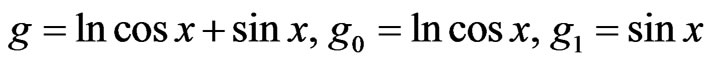
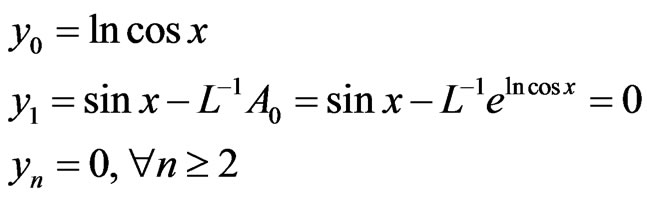
Then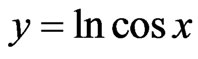 .
.
M3: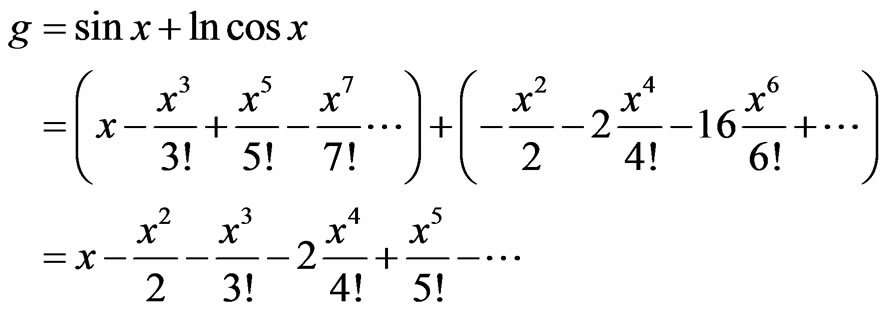
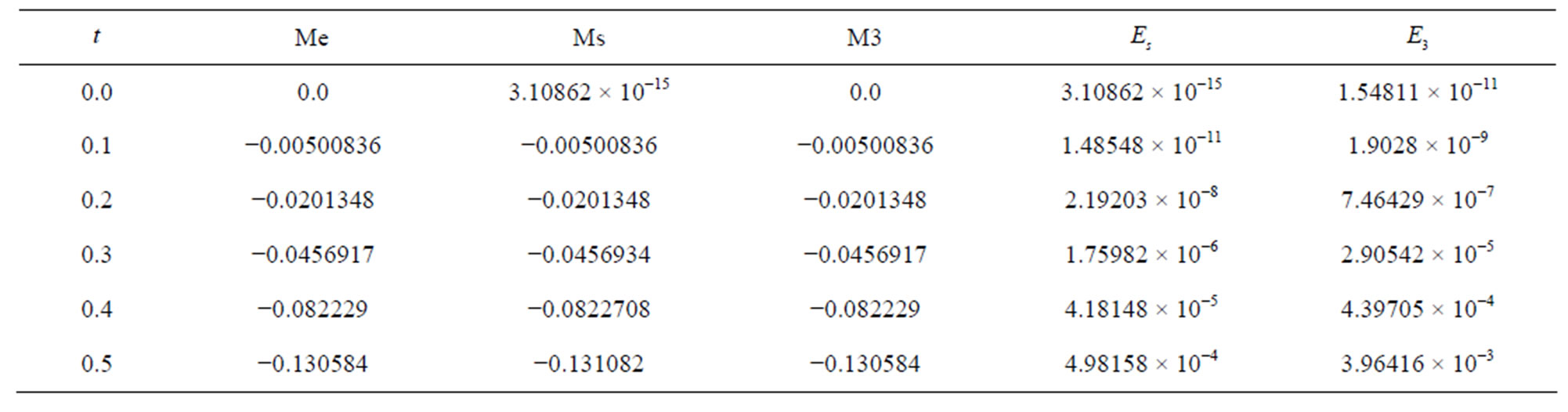
Table 1. comparison of absolute errors between the exact solution and approximate solutions Ms and M3.

Figure 1. comparison between the exact solution and approximate solutions Ms.
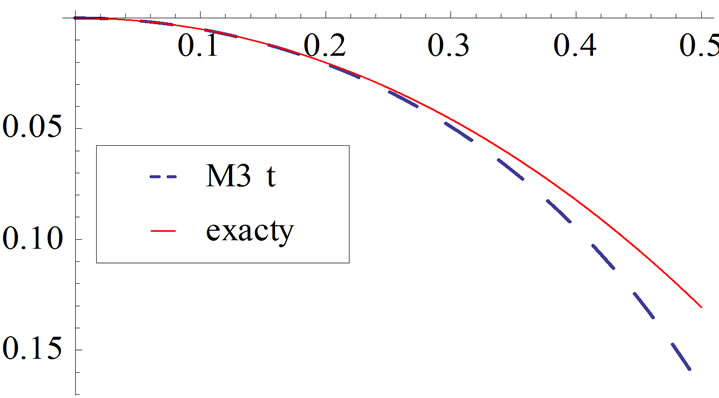
Figure 2. comparison between the exact solution and approximate solutions M3.
Then
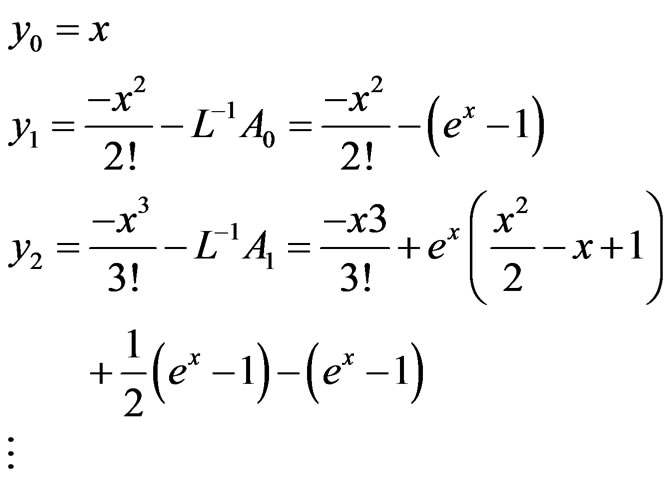
The comparison of absolute errors between the exact solution and approximate solution M3 introduce in Table 1 and Figure 2.
M4: Let
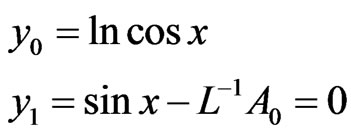
Then
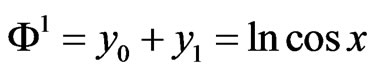
Then the exact solution is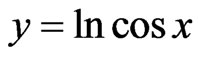 .
.
M5: Let
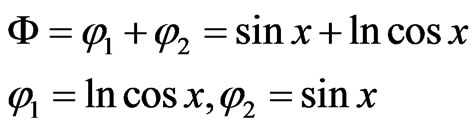
Clearly 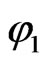 satisfy
satisfy  and by verifying that
and by verifying that 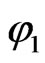 justified the differential equation.
justified the differential equation.
Hence,  is the exact solution.
is the exact solution.
REFERENCES
- G. Adomian, “Solving Frontier Problems of Physics: The Decomposition Method,” Springer, New York, 1993.
- G. Adomian and R. Rach, “Modified Adomian Polynomials,” Mathematical and Computer Modelling, Vol. 24, No. 11, 1996, pp. 39-46.
- Y. Cherruault, G. Adomian, K. Abbaoui and R. Rach, “Further Remarks on Convergence of Decomposition Method,” International Journal of Bio-Medical Computing, Vol. 38, No. 1, 1995, pp. 89-93. doi:10.1016/0020-7101(94)01042-Y
- F. A. Hendi, H. O. Bakodah, M. Almazmumy and H. Alzumi, “A Simple Program for Solving Nonlinear Initial Value Problem Using Adomian Decomposition Method,” International Journal of Research and Reviews in Applied Sciences, Vol. 12, No. 3, 2012.
- A.-M. Wazwaz, “The Modified Decomposition Method and Padé Approximants for Solving the Thomas-Fermi Equation,” Applied Mathematics and Computation, Vol. 105, No. 1, 1999, pp. 11-19. doi:10.1016/S0096-3003(98)10090-5
- A.-M. Wazwaz, “A Reliable Modification of Adomian Decomposition Method,” Applied Mathematics Computation, Vol. 102, No. 1, 1999, pp. 77-86. doi:10.1016/S0096-3003(98)10024-3
- A.-M. Wazwaz, Adomian Decomposition Dethod for a Deliable Dreatment of the Edman-Flower Dquation,” Applied Mathematics and Computation, Vol. 161, No. 2, 2005, pp. 543-560. doi:10.1016/j.amc.2003.12.048
- X.-G. Luo, “A Two-Step Adomian Decomposition Method,” Applied Mathematics and Computation, Vol. 170, No. 1, 2005, pp. 570-583. doi:10.1016/j.amc.2004.12.010
- B.-Q. Zhang, Q.-B. Wu and X.-G. Luo, “Experimentation with Two-Step Adomian Decomposition Method to Solve Evolution Models,” Applied Mathematics and Computation, Vol. 175, No. 2, 2006, pp. 1495-1502. doi:10.1016/j.amc.2005.08.029
- E. Babolian and S. Javadi, “Restarted Adomian Method for Algebraic Equations,” Applied Mathematics and Computation, Vol. 146, No. 2-3, 2003, pp. 533-541. doi:10.1016/S0096-3003(02)00603-3
- E. Babolian, S. Javadi and H. Sadehi, “Restarted Adomian Method for Integral Equations,” Applied Mathematics and Computation, Vol. 153, No. 2, 2004, pp. 353-359. doi:10.1016/S0096-3003(03)00636-2
- C. Jin and M. Liu, “A New Modification of Adomian Decomposition Method for Solving a Kind of Evolution Equations,” Applied Mathematics and Computation, Vol. 169, No. 2, 2005, pp. 953-962. doi:10.1016/j.amc.2004.09.072
- H. Jafari and V. Daftardar-Gejji, “Revised Adomian Decomposition Method for Solving a System of Nonlinear Equations,” Applied Mathematics and Computation, Vol. 175, No. 1, 2006, pp. 1-7. doi:10.1016/j.amc.2005.07.010
- H. Jafari and V. Daftardar-Gejji, “Revised Adomian DeComposition Method for Solving a System of Ordinary and Fractional Differential Equations,” Applied Mathematics and Computation,” Vol. 181, No. 1, 2006, pp. 598-608. doi:10.1016/j.amc.2005.12.049
- M. M. Hosseini and H. Nasabzadeh, “Modified Adomian Decomposition Method for Specific Second Order Ordinary Differential Equations,” Applied Mathematics and Computation, Vol. 186, No.1, 2007, pp. 117-123. doi:10.1016/j.amc.2006.07.094
- Y. Q. Hasan and L. M. Zhu, “Modified Adomian Decomposition Method for Singular Initial Value Problems in the Second Order Ordinary Differential Equations,” Surveys in Mathematics and Its Applications, Vol. 3, 2008, pp. 183-193.
- P. Pue-on and N. Viryapong, “Modified Adomian Decomposition Method for Solving Particular Third-Order Ordinary Differential Equations,” Applied Mathematical Science, Vol. 6, No. 30, 2012, pp. 1463-1469.
- G. Adomian, “Nonlinear Stochastic Operator Equataions,” Academic Press, San Diego, 1986.
- Y. Cherruault, “Convergence of Adomians Method,” Kybernetes, Vol. 18, No. 2, 1989, pp. 31-38. doi:10.1108/eb005812
- Y. Cherruault and G. Adomian, “Decomposition Method: A New Proof of Convergence,” Mathematical and Computer Modelling, Vol. 18, No. 12, 1993, pp.103-106. doi:10.1016/0895-7177(93)90233-O
- K. Abbaoui and Y. Cherruault, “Convergence of Adomian’s Method Applied to Differential Equations,” Computers & Mathematics with Applications, Vol. 28, No. 5, 1994, pp. 103-109. doi:10.1016/0898-1221(94)00144-8
- K. Abbaoui and Y. Cherruault, “Convergence of Adomian Method Applied to Nonlinear Equations,” Mathematical and Computer Modelling, Vol. 20, No. 9, 1994, pp. 69-73. doi:10.1016/0895-7177(94)00163-4
- H. Alzumi, F. A. Hendi, H. O. Bakodah and M. Almazmumy, “Convergence Analysis of Some Decomposition Method for Initial Value Problem of the First Order,” 2012.
- G. Adomian and R. Rach, “Noise Terms in Decomposition Solution Series,” Computers & Mathematics with Applications, Vol. 24, No. 11, 1992, pp. 61-64. doi:10.1016/0898-1221(92)90031-C
- G. Adomian and R. Rach, “The Noisy Convergence Phenomena in Decomposition Method Solutions,” Journal of Computational and Applied Mathematics, Vol. 15, No. 3, 1986, pp. 379-381. doi:10.1016/0377-0427(86)90228-1
- A.-M. Wazwaz, “Necessary Conditions for the Appearance of Noise Terms in Decomposition Solution Series,” Applied Mathematics and Computation, Vol. 81, No. 2-3, 1997, pp. 265-274. doi:10.1016/S0096-3003(95)00327-4
- A.-M. Wazwaz, “The Existence of Noise Terms for Systems of Inhomogeneous Differential and Integral Equations,” Applied Mathematics and Computation, Vol. 146, No. 1, 2003, pp. 81-92. doi:10.1016/S0096-3003(02)00527-1
- R. Rach, G. Adomian and R. E. Meyers, “A Modified Decomposition,” Computers & Mathematics with Applications, Vol. 23, No. 1, 1992, pp. 17-23. doi:10.1016/0898-1221(92)90076-T
- A.-M. Wazwaz, “Partial Differential Equations and Solitary Waves Theory,” Springer, New York, 2009. doi:10.1007/978-3-642-00251-9
- A.-M. Wazwaz and S. M. El-sayed, “A New Modification of the Adomian Decomposition Method for Linear and Nonlinear Operators,” Applied Mathematics and Computation, Vol. 122, No. 3, 2001, pp. 393-405. doi:10.1016/S0096-3003(00)00060-6
- H. O. Bakodah, “Some Modification of Adomian Decomposition Method Applied to Nonlinear System of Fredholm Integral Equations of the Second Kind,” International Journal of Contemporary Mathematical Sciences, Vol. 7, No. 19, 2012, pp. 929-942.

