American Journal of Operations Research
Vol.04 No.04(2014), Article ID:48101,11 pages
10.4236/ajor.2014.44026
Using DEA and AHP for Ratio Analysis
Mohammad Sadegh Pakkar
Faculty of Management, Laurentian University, Sudbury, Canada
Email: ms_pakkar@laurentian.ca
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 May 2014; revised 2 July 2014; accepted 10 July 2014
ABSTRACT
This research proposes an integrated approach to the Data Envelopment Analysis (DEA) and Ana- lytic Hierarchy Process (AHP) methodologies for ratio analysis. According to this, we compute two sets of weights of ratios in the DEA framework. All ratios are treated as outputs without explicit inputs. The first set of weights represents the most attainable efficiency level for each Decision Making Unit (DMU) in comparison to the other DMUs. The second set of weights represents the relative priority of output-ratios using AHP. We assess the performance of each DMU in terms of the relative closeness to the priority weights of output-ratios. For this purpose, we develop a pa- rametric goal programming model to measure the deviations between the two sets of weights. In- creasing the value of a parameter in a defined range of efficiency loss, we explore how much the deviations can be improved to achieve the desired goals of the decision maker. This may result in various ranking positions for each DMU in comparison to the other DMUs. An illustrated example of eight listed companies in the steel industry of China is used to highlight the usefulness of the proposed approach.
Keywords:
Data Envelopment Analysis, Analytic Hierarchy Process, Ratio Analysis, Goal Programming

1. Introduction
Ratio analysis is a commonly used analytical tool for measuring the relative performance of a Decision Making Units (DMUs) by focusing on one input/output at a time [1] . In practical applications, the weighted average of a set of individual ratios is applied in order to produce a single measure of performance from various ratios. How- ever, the appropriate assignment of weights in this approach has been an issue of controversy for researchers. Fortunately, the development of modern Operations Research/Management Science (OR/MS) has provided us with two powerful methods called Data Envelopment Analysis (DEA) and Analytic Hierarchy Process (AHP) which can be used to derive ratio weights.
DEA is a data-oriented approach for assessing the relative efficiency of Decision Making Units (DMUs) that use multiple inputs to produce multiple outputs. The standard DEA models are formulated using absolute nu- merical input and output data [2] . In order to use ratio data in the DEA framework, ratio-based DEA models were developed as a combination of DEA methodology and ratio analysis [3] - [5] .
However, the weights provided by (ratio-based) DEA models are often unrealistic. Assigning the extremely large or small weights to certain (ratio) data may be undesirable for some Decision Makers (DMs) because it may categorize a DMU as efficient for unlikely weight combinations. Hence, there is a point to argue that the relative priority of (ratio) data should be taken into account in efficiency assessments.
On the other hand, AHP is a multi-attribute decision-making method that can reflect a priori information about the relative priority of (ratio) data in efficiency assessments. AHP usually involves three stages for gene- rating weights. These stages are the decomposition into a hierarchy, comparative judgments, and synthesis of priorities [6] . AHP, however, seldom is used as a stand-alone tool in recent years. Rather, it is combined with other OR/MS models [7] . The most common approach is the imposition of weight restrictions in DEA models. Referring to the literature, AHP can estimate the bounds of the following restrictions in DEA:
・ Absolute weight restrictions. These restrictions directly impose upper and (or) lower bounds on the weights of inputs (outputs) using AHP [8] .
・ Relative weight restrictions. These restrictions limit the relationship between the weights of inputs (outputs) using AHP [9] - [13] .
・ Virtual weight restrictions. A single virtual input (output) is defined as the weighted sum of all inputs (out- puts). We refer to the proportion of each component of such sum as the “virtual weight” of an input (output). These restrictions limit virtual weights using AHP [14] [15] .
・ Restrictions on input (output) units. These restrictions impose bounds on changes of inputs (outputs) while the relative importance of such changes is computed using AHP [16] .
There are a number of other methods that do not necessarily apply additional restrictions to a DEA model. Such as converting the qualitative data in DEA to the quantitative data using AHP [17] - [24] , ranking the effi- cient/inefficient units in DEA models using AHP in a two stage process [25] - [27] , weighting the efficiency scores obtained from DEA using AHP [28] , weighting the inputs and outputs in the DEA structure [29] - [31] , constructing a convex combination of weights using AHP and DEA [32] and estimating the missing data in DEA using AHP [33] .
Recently the author has applied AHP weights as weight bounds into a two-level DEA model [34] and a com- mon set of weights (CSW) model [35] . Using a similar approach, this research applies AHP in the ratio-based DEA framework to develop a new integration between DEA, AHP and ratio analysis theory.
2. Methodology
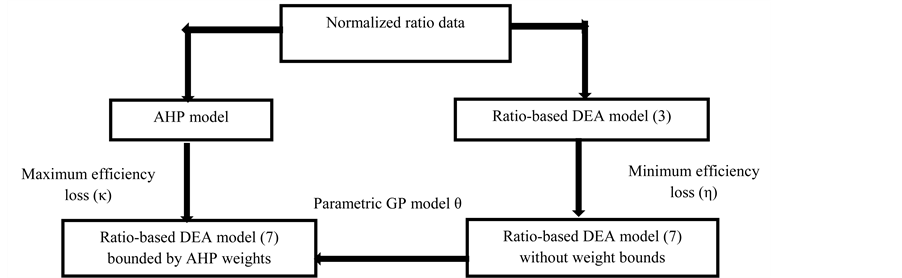
This research has been organized to proceed along the following stages (Figure 1):
1) Computing the efficiency of each DMU using ratio-based DEA Model (3) without explicit inputs. The computed efficiencies are applied in Model (7).
2) Computing the priority weights of output-ratios for all DMUs using AHP, which impose weight bounds into Model (7).
Figure 1. An integrated approach to DEA, AHP and ratio-analysis.
3) Obtaining an optimal set of weights for each DMU using ratio-based DEA Model (7) (minimum efficiency loss η).
4) Obtaining an optimal set of weights for each DMU using Model (7) bounded by AHP (maximum efficiency loss κ). Note that if the AHP weights are added to (7), we obtain Model (9).
5) Measuring the performance of each DMU in terms of the relative closeness to the priority weights of out- put-ratios. For this purpose, we develop a parameter goal programming model. Increasing a parameter in a de- fined range of efficiency loss, we explore how much a DM can achieve its goals. This may result in various ranking positions for a DMU in comparison to the other DMUs.
2.1. A Ratio-Based DEA Model
A ratio-based DEA model can be formulated similar to a classical DEA model without explicit inputs [36] [37] . Since the data in a DEA model are in different units of measurements and some output-ratios are negative, the normalized counterparts of output-ratios are computed as follows [38] :
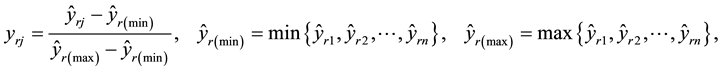 (1)
(1)
where
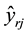 is the output-ratio
is the output-ratio
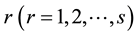 for DMU
for DMU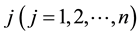 .
.
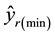 and
and
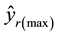 are the mini- mum and maximum output-ratios
are the mini- mum and maximum output-ratios
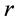 for all DMUs, respectively. Assume now DMUs have the unit input
for all DMUs, respectively. Assume now DMUs have the unit input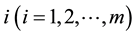 . Then the fractional CCR-DEA model with normalized (ratio) data can be developed as follows [39] :
. Then the fractional CCR-DEA model with normalized (ratio) data can be developed as follows [39] :
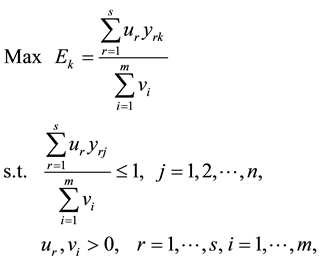 (2)
(2)
where
 is the relative efficiency of DMU under assessment.
is the relative efficiency of DMU under assessment.
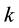 is the index for the DMU under assessment where
is the index for the DMU under assessment where
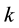 ranges over
ranges over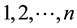 .
.
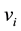 and
and
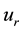 are the weights of input
are the weights of input





Model (3) looks like a DEA model without inputs that combines the standard DEA methodology with ratio analysis.
2.2. The AHP Formulation
There are basically three steps for considering decision problems by AHP namely: 1) Decomposition; 2) Pair- wise Comparisons and Judgment Matrix; and 3) Synthesis [6] .
Step 1: Decomposition. This step includes decomposition of the decision problem into elements according to their common characteristics and the formation of a hierarchical model having different levels. In this study, the AHP hierarchical model has three levels: problem objective, criteria and sub-criteria. The problem objective is to prioritize the output-ratios, the criteria are the categories of output-ratios, and the sub-criteria are various out- put-ratios that are organized into these categories (Figure 2).
Step 2: Pairwise Comparisons and Judgment Matrix. In this step, a decision maker makes a pairwise compari- son matrix of different criteria, denoted by




Step 3: Synthesis. In this step, the AHP method obtains the priority weights of criteria by computing the ei- genvector of matrix




In a similar way, the priority weights of sub-criteria under each criterion is obtained by computing the eigen- vector of matrix



To determine whether or not the inconsistency in a comparison matrix is reasonable the random consistency ratio,


where


2.3. A Ratio-Based DEA Model Using AHP
We develop our formulation based on a simplified version of the generalized distance model (see for example [40] and [41] ) for output-ratios. Let






Figure 2. The AHP hierarchical model for prioritizing ratios.
Model (7) identifies the minimum efficiency loss η (eta) needed to arrive at an optimal set of weights. The first constraint ensures that each DMU loses no more than η of its best attainable efficiency,

To obtain the weight bounds for the weights of output-ratios in Model (7), this study aggregates the priority weights of two different levels in AHP as follows:

where









In order to estimate the maximum efficiency loss


The first set of constraints changes the priority weights of output-ratios to weights for the new system by means of a scaling factor

2.4. A Parametric Goal Programming Model
In this stage, we develop a parametric goal programming model that can be solved repeatedly to generate the various sets of weights for the discrete values of the parameter


where



Because the range of deviations computed by the objective function is different for each DMU, it is necessary to normalize it by using relative deviations rather than absolute ones [43] . Hence, the normalized deviations can be computed by:

where






3. A Numerical Example: The Financial Performance Assessment
In this section we present the application of the proposed approach to assess the financial performance of eight listed companies in the steel industry of China. The companies’ financial ratios, adopted from [44] , is presented in Table 1.
Table 2 depicts the hierarchical structure of financial ratios and the corresponding priority weights in the AHP model as constructed in [44] . There are five categories of financial ratios at the criteria level. Each one includes three different ratios at the sub-criteria level.
Solving Model (7) for the DMU under assessment with normalized ratio data, we obtain an optimal set of weights with minimum efficiency loss,

On the other hand, solving Model (9) for the DMU under assessment, we adjust the priority weights of out- put-ratios obtained from AHP in such a way that they become compatible with the weights’ structure in the ratio- based DEA models.
Table 3 presents the optimal weights of output-ratios as well as its scaling factor for the most efficient per- former, DMU5.
It should be noted that the priority weights of AHP (Table 2) used for incorporating weight bounds on the weights of output-ratios are obtained as


Table 1. Financial market data (ratios) for eight listed companies in China’s steel industry.
Table 2. The AHP hierarchical model*.
*







Table 3. Optimal weights of output-ratios of Model (9) for DMU5.
The maximum efficiency loss for the DMU under assessment to achieve the corresponding weights in Model (9) is equal to


Going one step further to the solution process of the parametric goal programming model in (10) we proceed to the estimation of total deviations from the AHP weights for each DMU while the parameter




Table 5 shows that DMU5 is the best performer in terms of efficiency and the relative closeness to the priority weights of output-ratios in comparison to the other DMUs. Nevertheless, increasing the value of




Table 4. Minimum and maximum efficiency loss.
Table 5. The ranking position of each DMU based on the minimum distance to priority weights of output-ratios.
Figure 3. The relative closeness to the priority weights of ratios [∆(θ)], versus efficiency loss (θ) for each DMU.
4. Conclusion
We develop an integrated approach based on DEA and AHP methodologies for ratio analysis. We define two sets of weights of ratios in the DEA framework. All ratios are treated as outputs without implicit inputs. The first set represents the weights of output-ratios with minimum efficiency loss. The second set represents the correspond- ing priority weights using AHP with maximum efficiency loss. We assess the performance of each DMU in comparison to the other DMUs based on the relative closeness of the first set of weights to the second set of weights. Improving the measure of relative closeness in a defined range of efficiency loss, we explore the vari- ous ranking positions for the DMU under assessment in comparison to the other DMUs.
Cite this paper
Mohammad SadeghPakkar, (2014) Using DEA and AHP for Ratio Analysis. American Journal of Operations Research,04,268-279. doi: 10.4236/ajor.2014.44026
References
- 1. Sigaroudi, S. (2010) Incorporating Ratios in DEA—Applications to Real Data. Master Thesis, University of Toronto, Toronto.
- 2. Cooper, W.W., Seiford, L.M. and Zhu, J. (2004) Handbook on Data Envelopment Analysis. Kluwer Academic Publishers, Norwel.
- 3. Wu, D., Liang, L., Huang, Z. and Li, S. (2005) Aggregated Ratio Analysis in DEA. International Journal of Information Technology & Decision Making, 4, 369-384.
http://dx.doi.org/10.1142/S0219622005001593 - 4. Despic, O., Despic, M. and Paradi, J.C. (2007) DEA-R: Ratio-Based Comparative Efficiency Model, Its Mathematical Relation to DEA and Its Use in Applications. Journal of Productivity Analysis, 28, 33-44.
http://dx.doi.org/10.1007/s11123-007-0050-x - 5. Wei, C.K., Chen, L.C., Li, R.K. and Tsai, C.H. (2011) Using the DEA-R Model in the Hospital Industry to Study the Pseudo-Inefficiency Problem. Expert Systems with Applications, 38, 2172-2176.
http://dx.doi.org/10.1016/j.eswa.2010.08.003 - 6. Saaty, T.S. (1980) The Analytic Hierarchy Process. McGraw-Hill, New York.
- 7. Vaidya, O.S. and Kumar, S. (2006) Analytic Hierarchy Process: An Overview of Applications. European Journal of Operational Research, 169, 1-29.
http://dx.doi.org/10.1016/j.ejor.2004.04.028 - 8. Entani, T., Ichihashi, H. and Tanaka, H. (2004) Evaluation Method Based on Interval AHP and DEA. Central European Journal of Operations Research, 12, 25-34.
- 9. Lee, A.H.I., Lin, C.Y., Kang, H.Y. and Lee, W.H. (2012) An Integrated Performance Evaluation Model for the Photovoltaics Industry. Energies, 5, 1271-1291.
http://dx.doi.org/10.3390/en5041271 - 10. Liu, C.M., Hsu, H.S., Wang, S.T. and Lee, H.K. (2005) A Performance Evaluation Model Based on AHP and DEA, Journal of the Chinese Institute of Industrial Engineers, 22, 243-251.
http://dx.doi.org/10.1080/10170660509509294 - 11. Takamura, Y. and Tone, K. (2003) A Comparative Site Evaluation Study for Relocating Japanese Government Agencies out of Tokyo. Socio-Economic Planning Sciences, 37, 85-102.
http://dx.doi.org/10.1016/S0038-0121(02)00049-6 - 12. Tseng, W., Yang, C. and Wang, D. (2009) Using the DEA and AHP Methods on the Optimal Selection of IT Strategic Alliance Partner. Proceedings of the 2009 International Conference on Business and Information (BAI 2009), 6, 1-15.
- 13. Kong, W. and Fu, T. (2012) Assessing the Performance of Business Colleges in Taiwan Using Data Envelopment Analysis and Student Based Value-Added Performance Indicators. Omega, 40, 541-549.
http://dx.doi.org/10.1016/j.omega.2011.10.004 - 14. Premachandra, I.M. (2001) Controlling factor weights in data envelopment analysis by Incorporating decision maker’s value judgement: An approach based on AHP, Journal of Information and Management Science, 12, 1-12.
- 15. Shang, J. and Sueyoshi, T. (1995) Theory and Methodology—A Unified Framework for the Selection of a Flexible Manufacturing System. European Journal of Operational Research, 85, 297-315.
http://dx.doi.org/10.1016/0377-2217(94)00041-A - 16. Lozano, S. and Villa, G. (2009) Multiobjective Target Setting in Data Envelopment Analysis Using AHP. Computers & Operations Research, 36, 549-564.
http://dx.doi.org/10.1016/j.cor.2007.10.015 - 17. Azadeh, A., Ghaderi, S.F. and Izadbakhsh, H. (2008) Integration of DEA and AHP with Computer Simulation for Railway System Improvement and Optimization. Applied Mathematics & Computation, 195, 775-785.
http://dx.doi.org/10.1016/j.amc.2007.05.023 - 18. Ertay, T., Ruan, D. and Tuzkaya, U.R. (2006) Integrating Data Envelopment Analysis and Analytic Hierarchy for the Facility Layout Design in Manufacturing Systems. Information Sciences, 176, 237-262.
http://dx.doi.org/10.1016/j.ins.2004.12.001 - 19. Jyoti, Banwet, D.K. and Deshmukh, S.G. (2008) Evaluating Performance of National R&D Organizations Using Integrated DEA-AHP Technique. International Journal of Productivity and Performance Management, 57, 370-388.
http://dx.doi.org/10.1108/17410400810881836 - 20. Korpela, J., Lehmusvaara, A. and Nisonen, J. (2007) Warehouse Operator Selection by Combining AHP and DEA Methodologies. International Journal of Production Economics, 108, 135-142.
http://dx.doi.org/10.1016/j.ijpe.2006.12.046 - 21. Lin, M., Lee, Y. and Ho, T. (2011) Applying Integrated DEA/AHP to Evaluate the Economic Performance of Local Governments in China. European Journal of Operational Research, 209, 129-140.
http://dx.doi.org/10.1016/j.ejor.2010.08.006 - 22. Ramanathan, R. (2007) Supplier Selection Problem: Integrating DEA with the Approaches of Total Cost of Ownership and AHP. Supply Chain Management, 12, 258-261.
http://dx.doi.org/10.1108/13598540710759772 - 23. Yang, T. and Kuo, C. (2003) A Hierarchical AHP/DEA Methodology for the Facilities Layout Design Problem. European Journal of Operational Research, 147, 128-136.
http://dx.doi.org/10.1016/S0377-2217(02)00251-5 - 24. Raut, R.D. (2011) Environmental Performance: A Hybrid Method for Supplier Selection Using AHP-DEA. International Journal of Business Insights & Transformation, 5, 16-29.
- 25. Ho, C.B. and Oh, K.B. (2010) Selecting Internet Company Stocks Using a Combined DEA and AHP Approach. International Journal of Systems Science, 41, 325-336.
http://dx.doi.org/10.1080/00207720903326902 - 26. Jablonsky, J. (2007) Measuring the Efficiency of Production Units by AHP Models. Mathematical & Computer Modelling, 46, 1091-1098.
http://dx.doi.org/10.1016/j.mcm.2007.03.007 - 27. Sinuany-Stern, Z., Mehrez, A. and Hadad, Y. (2000) An AHP/DEA Methodology for Ranking Decision Making Units. International Transactions in Operational Research, 7, 109-124.
http://dx.doi.org/10.1111/j.1475-3995.2000.tb00189.x - 28. Chen, T.Y. (2002) Measuring Firm Performance with DEA and Prior Information in Taiwan’s Banks. Applied Economics Letters, 9, 201-204. http://dx.doi.org/10.1080/13504850110057947
- 29. Cai, Y.Z. and Wu, W.J. (2001) Synthetic Financial Evaluation by a Method of Combining DEA with AHP. International Transactions in Operational Research, 8, 603-609.
http://dx.doi.org/10.1111/1475-3995.00336 - 30. Feng, Y.J., Lu, H. and Bi, K. (2004) An AHP/DEA Method for Measurement of the Efficiency of R&D Management Activities in Universities. International Transactions in Operational Research, 11, 181-191.
http://dx.doi.org/10.1111/j.1475-3995.2004.00450.x - 31. Kim, T. (2000) Extended Topics in the Integration of Data Envelopment Analysis and the Analytic Hierarchy Process in Decision Making. Ph.D. Thesis, Agricultural & Mechanical College, Louisiana State University, Baton Rouge.
- 32. Liu, C. and Chen, C. (2004) Incorporating Value Judgments into Data Envelopment Analysis to Improve Decision Quality for Organization. Journal of American Academy of Business, Cambridge, 5, 423-427.
- 33. Saen, R.F., Memariani, A. and Lotfi, F.H. (2005) Determining Relative Efficiency of Slightly Non-Homogeneous Decision Making Units by Data Envelopment Analysis: A Case Study in IROST. Applied Mathematics and Computation, 165, 313-328.
http://dx.doi.org/10.1016/j.amc.2004.04.050 - 34. Pakkar, M.S. (2014) An Integrated Approach Based on DEA and AHP. Computational Management Science.
http://dx.doi.org/10.1007/s10287-014-0207-9 - 35. Pakkar, M.S. (2012) An Integrated Approach to the DEA and AHP Methodologies in Decision Making. In: Charles, V. and Kumar, M., Eds., Data Envelopment Analysis and Its Applications to Management, Cambridge Scholars Publishing, Newcastle upon Tyne, 136-149.
- 36. Liu, W.B., Zhang, D.Q., Meng, W., Li, X.X. and Xu, F. (2011) A Study of DEA Models without Explicit Inputs. Omega, 39, 472-480.
http://dx.doi.org/10.1016/j.omega.2010.10.005 - 37. Mozaffari, M., Gerami, J. and Jablonsky, J. (2014) Relationship between DEA Models without Explicit Inputs and DEA-R Models. Central European Journal of Operations Research, 22, 1-12.
http://dx.doi.org/10.1007/s10100-012-0273-4 - 38. Sahoo, B.K. and Meera, E. (2008) A Comparative Application of Alternative DEA Models in Selecting Efficient Large Cap Market Securities in India. International Journal of Management Perspectives, 1, 62-75.
- 39. Charnes, A., Cooper, W.W. and Rhodes, E. (1978) Measuring the Efficiency of Decision Making Units. European Journal of Operational Research, 2, 429-444.
http://dx.doi.org/10.1016/0377-2217(78)90138-8 - 40. Mavi, R.K., Mavi, N.K. and Mavi, L.K. (2012) Compromise Programming for Common Weight Analysis in Data Envelopment Analysis. American Journal of Scientific Research, Issue 45, 90-109.
- 41. Hashimoto, A. and Wu, D.A. (2004) A DEA-Compromise Programming Model for Comprehensive Ranking. Journal of the Operation Research Society of Japan, 47, 73-81.
- 42. Podinovski, V.V. (2004) Suitability and Redundancy of Non-Homogeneous Weight Restrictions for Measuring the Relative Efficiency in DEA. European Journal of Operational Research, Amsterdam, 154, 380-395.
http://dx.doi.org/10.1016/S0377-2217(03)00176-0 - 43. Romero, C. and Rehman, T. (2003) Multiple Criteria Analysis for Agricultural Decisions. 2nd Edition, Elsevier, Amsterdam.
- 44. Li, H.Y., Zhang, C. and Zhao, D. (2010) Stock Investment Value Analysis Model Based on AHP and Gray Relational Degree. Management Science and Engineering, 4, 1-6.
Appendix A. The Measure of Relative Closeness to the Priority Weights of Ratios [∆(θ)] Verses Efficiency Loss [θ] for Each DMU