American Journal of Operations Research
Vol. 2 No. 2 (2012) , Article ID: 19941 , 8 pages DOI:10.4236/ajor.2012.22025
The MX/M/1 Queue with Multiple Working Vacation
Department of Mathematics Education, College of Education and Human Sciences, Yokohama National University, Yokohama, Japan
Email: yutakab@ynu.ac.jp
Received April 19, 2012; revised May 20, 2012; accepted June 2, 2012
Keywords: MX/M/1 Queue; Multiple Working Vacation; Probability Generating Function; Waiting Time Distribution; Stochastic Decomposition
ABSTRACT
We study a batch arrival MX/M/1 queue with multiple working vacation. The server serves customers at a lower rate rather than completely stopping service during the service period. Using a quasi upper triangular transition probability matrix of two-dimensional Markov chain and matrix analytic method, the probability generating function (PGF) of the stationary system length distribution is obtained, from which we obtain the stochastic decomposition structure of system length which indicates the relationship with that of the MX/M/1 queue without vacation. Some performance indices are derived by using the PGF of the stationary system length distribution. It is important that we obtain the Laplace Stieltjes transform (LST) of the stationary waiting time distribution. Further, we obtain the mean system length and the mean waiting time. Finally, numerical results for some special cases are presented to show the effects of system parameters.
1. Introduction
Vacation queues have been investigated for over two decades as a very useful tool for modeling and analyzing computer systems, communication networks, manufacturing and production systems and many others. The details can be seen in the monographs of Takagi [1] and Tian and Zhang [2], the survey of Doshi [3]. However, in these models, the server stops the original work in the vacation period and can not come back to the regular busy period until the vacation period ends.
Recently, Servi and Finn [4] introduced the working vacation policy, in which the server works at a different rate rather than completely stopping service during the vacation. They studied an M/M/1 queue with working vacations, and obtained the transform formulae for the distribution of the number of customers in the system and sojourn time in steady state, and applied these results to performance analysis of gateway router in fiber communication networks. During the working vacation models, the server can not come back to the regular busy period until the vacation period ends. Subsequently, Wu and Takagi [5] generalized the model in [4] to an M/G/1 queue with general working vacations. Baba [6] studied a GI/M/1 queue with working vacations by using the matrix analytic method. Banik et al. [7] analyzed the GI/ M/1/N queue with working vacations. Liu et al. [8] established a stochastic decomposition result in the M/M/1 queue with working vacations. Li et al. [9] established the conditional stochastic decomposition result in the M/G/1 queue with exponentially working vacations using matrix analytic approach.
For the batch arrival queues, Xu et al. [10] studied a batch arrival MX/M/1 queue with single working vacation. With the matrix analytic method, they derived the PGF of the stationary system length distribution, from which they got the stochastic decomposition result for the PGF of the stationary system length which indicates the evident relationship with that of the classical MX/M/1 queue without vacation. Furthermore, they found the upper bound and lower bound of the stationary waiting time in the Laplace transform order, from which they got the upper bound and lower bound of the waiting time.
In this paper, we study a batch arrival MX/M/1 queue with multiple working vacation. We obtain the PGF of the stationary system length distribution and the stochastic decomposition structure of system length which indicates the relationship with that of MX/M/1 queue without vacation. Although only the upper bound and lower bound of the stationary waiting time in the Laplace transform order are obtained in [10], we can obtain the exact LST of the stationary waiting time distribution.
The rest of this paper is organized as follows. In Section 2, the model of the MX/M/1 queue with multiple working vacation is described. In Section 3, we obtain the PGF of the stationary system length and its decomposition result which indicates the evident relationship with that of the classical MX/M/1 queue without vacation. Furthermore, we obtain the mean system length and several characteristic quantities. In Section 4, we obtain the LST of the stationary waiting time distribution. Numerical results for some special cases are presented in Section 5.
2. Model Description
Consider a batch arrival MX/M/1 queue with multiple working vacation. Customers arrive in batches according to a Poisson process with rate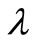 . The batch size
. The batch size 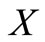 is a random variable and
is a random variable and
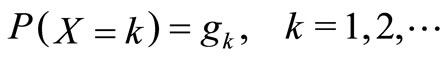
The PGF, the expectation and the second order moment of  are
are
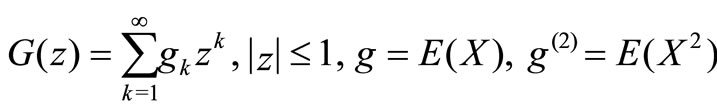 respectively.
respectively.
Service times in the regular busy period follows an exponential distribution with parameter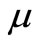 . Upon the completion of a service, if there is no customer in the system, the server begins a vacation and the vacation duration follows an exponential distribution with parameter
. Upon the completion of a service, if there is no customer in the system, the server begins a vacation and the vacation duration follows an exponential distribution with parameter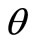 . During a working vacation period, arriving customers are served at a rate of
. During a working vacation period, arriving customers are served at a rate of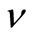 . When a vacation ends, if there are no customers in the queue, another vacation is taken. Otherwise, the server switches service rate from
. When a vacation ends, if there are no customers in the queue, another vacation is taken. Otherwise, the server switches service rate from 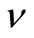 to
to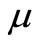 , and a regular busy period starts. The LST’s of the service time distribution in a regular busy period and the service time in a working vacation time are
, and a regular busy period starts. The LST’s of the service time distribution in a regular busy period and the service time in a working vacation time are
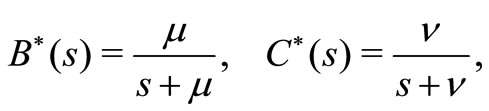 respectively.
respectively.
We assume that inter-arrival times, the service times and the working vacation times are mutually independent. Furthermore, the service discipline is first come first served (FCFS).
Let  be the number of customers in the system at time
be the number of customers in the system at time  and
and

Then the process 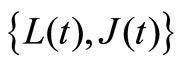 is a two-dimensional Markov chain with the state space
is a two-dimensional Markov chain with the state space
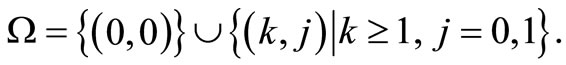
Using the lexicographical order for the states, the infinitesimal generator of the process 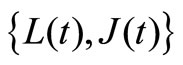 can be written as the Block-Jacobi matrix
can be written as the Block-Jacobi matrix

where

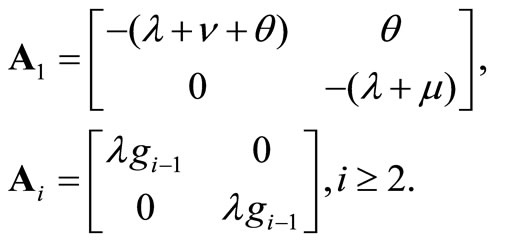
Since 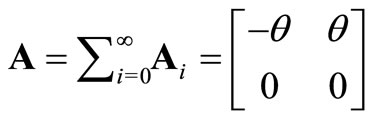 is reducible, it is found from Section 3.5 of Neuts [11] that the Markov chain is positive recurrent if and only if
is reducible, it is found from Section 3.5 of Neuts [11] that the Markov chain is positive recurrent if and only if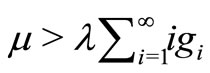 , that is,
, that is,
 .
.
3. Stationary System Length Distribution
In this section, we derive the PGF of stationary distribution for . Let
. Let  be the stationary limit of the process
be the stationary limit of the process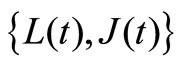 . Assume that
. Assume that
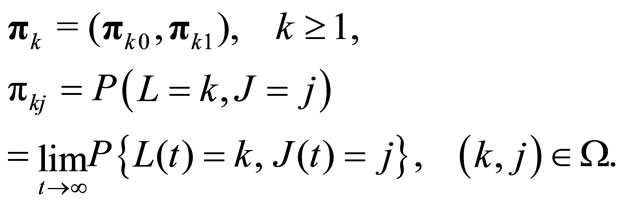
Based on the stationary equations, we have
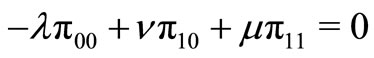 (1)
(1)
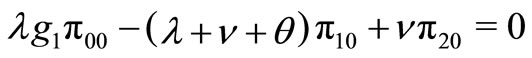 (2)
(2)
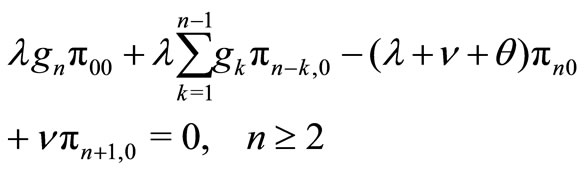 (3)
(3)
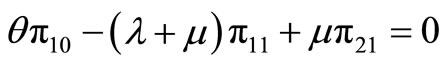 (4)
(4)
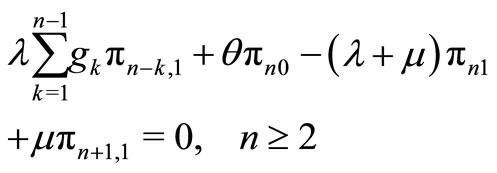 (5)
(5)
Define the probability generating functions (PGF’s)
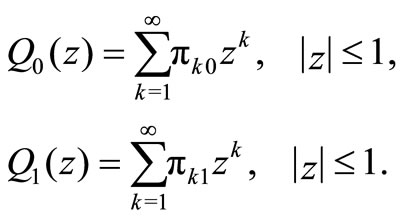
Then the PGF of stationary system length 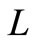 can be written as
can be written as
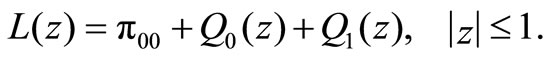
In order to prove Theorem 1 which states the stochastic decomposition structure of system length, the following lemma is necessary.
Lemma 1. The equation
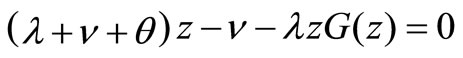
has the unique root  in the interval
in the interval .
.
Proof: We consider the function
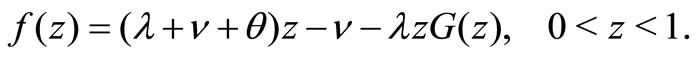
For any , we have
, we have
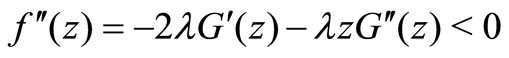 (6)
(6)
Therefore 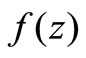 is a concave function in the interval
is a concave function in the interval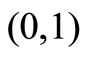 . Further,
. Further,
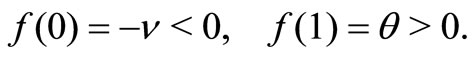 (7)
(7)
(6) and (7) indicate that the equation 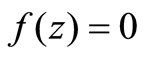 has the unique root
has the unique root 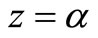 in the interval
in the interval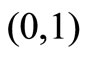 .
.
Remark 1. Lemma 1 in this paper is the same as Lemma 1 in Xu et al. [10]. But the proof in this paper is simpler than the proof in [10].
We have the following Theorem which proves the stochastic decomposition structure of system length.
Theorem 1. If 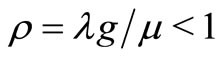 and
and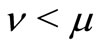 , the stationary system length
, the stationary system length 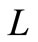 can be decomposed into the sum of two independent random variables,
can be decomposed into the sum of two independent random variables,
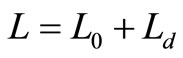
where 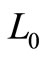 is the stationary system length in corresponding classical MX/M/1 queue without vacation and has the PGF
is the stationary system length in corresponding classical MX/M/1 queue without vacation and has the PGF
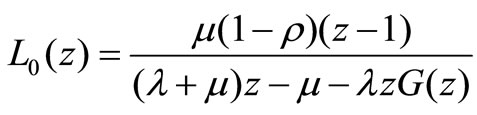 (8)
(8)
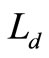 is the additional system length and has the PGF
is the additional system length and has the PGF
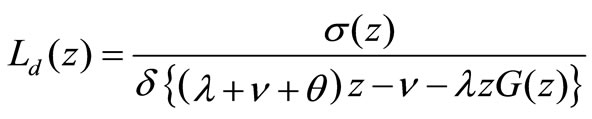 (9)
(9)
where
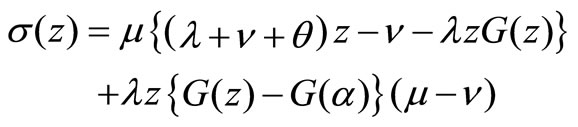
and
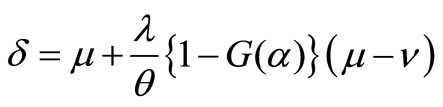
Proof: Multiplying the Equation (2) by 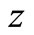 and each equation of (3) by
and each equation of (3) by 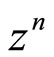 and summing up these equations, we have
and summing up these equations, we have
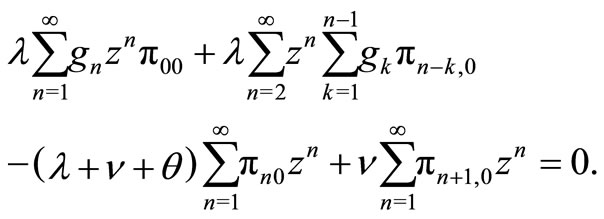
After calculations, we have
Therefore, we obtain
 (10)
(10)
Since  is an analytic function in
is an analytic function in , wherever the right-side of (10) has zeros in
, wherever the right-side of (10) has zeros in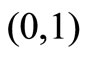 , so must the numerator. From Lemma 1, the denominator of
, so must the numerator. From Lemma 1, the denominator of  is equal to 0 if
is equal to 0 if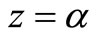 , so does the numerator. Substituting
, so does the numerator. Substituting  into the numerator of the right-hand side of (10), we have
into the numerator of the right-hand side of (10), we have
 (11)
(11)
Substituting (11) into (10), we have
 (12)
(12)
Similarly, multiplying the Equation (4) by 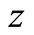 and each equation of (5) by
and each equation of (5) by 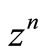 and summing up these equations, we have
and summing up these equations, we have

After calculations, we have
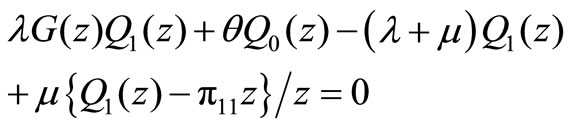
Therefore, we obtain
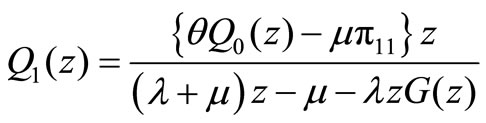 (13)
(13)
Since 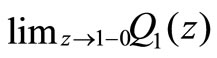 is finite and
is finite and 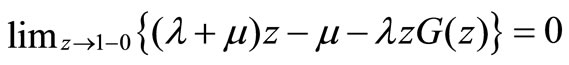 , we have
, we have
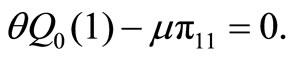 (14)
(14)
Substituting 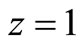 into (12), we have
into (12), we have
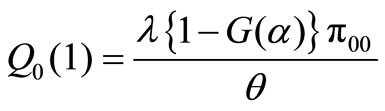 (15)
(15)
Using (14) and (15), we have
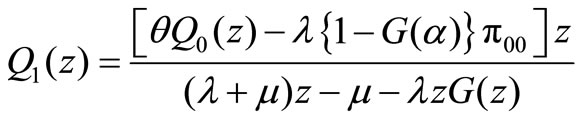 (16)
(16)
Using (10) and (16), we finally obtain
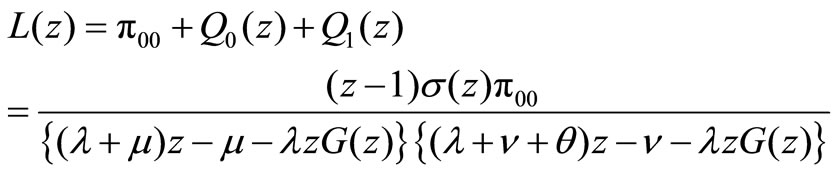 (17)
(17)
where
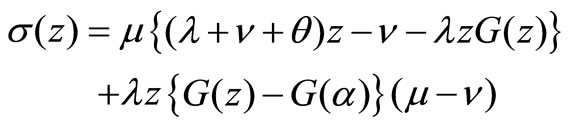
Using the condition that 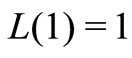 and L’Hospital’s rule, we have
and L’Hospital’s rule, we have
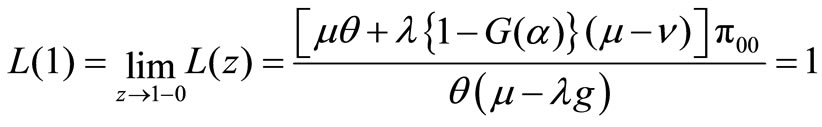
Obviously, the numerator and the denominator of the above expression are both positive since 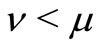 and
and . Furthermore, we have
. Furthermore, we have
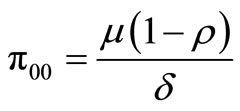 (18)
(18)
where
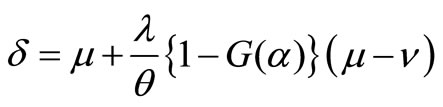
Substituting the expressions of 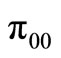 into (17), we finally obtain
into (17), we finally obtain
 (19)
(19)
Since ,
, 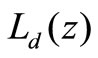 is a PGF. Therefore, we completes the proof of Theorem 1.
is a PGF. Therefore, we completes the proof of Theorem 1.
From Theorem 1, we can obtain two important characteristic quantities in the following two Corollaries.
Corollary 1. The mean of stationary system length 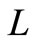 is given by
is given by

Proof: From (8), we have
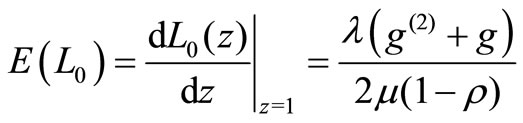
From (9), we have
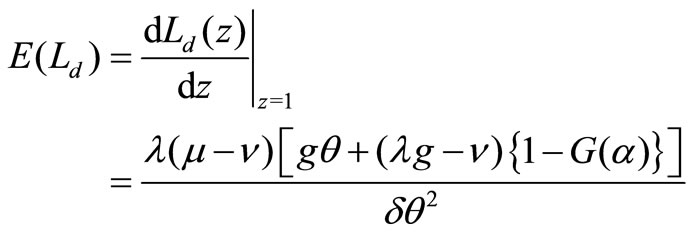
Therefore, we obtain
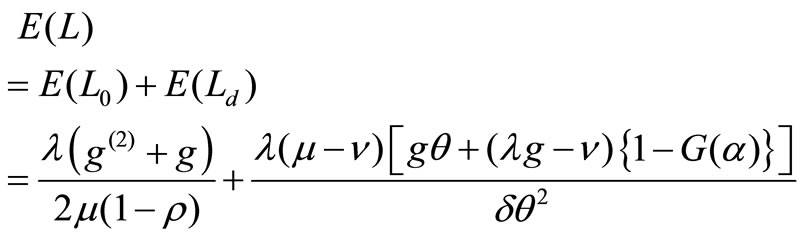
Corollary 2. The probability 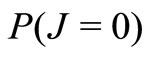 that the system is in a working vacation period and the probability
that the system is in a working vacation period and the probability 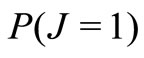 that the system is in a regular busy period are given by
that the system is in a regular busy period are given by

respectively.
Proof: Using (12) and (18), we have
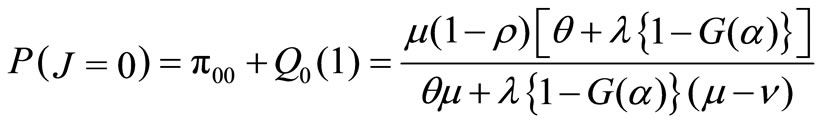
then we have
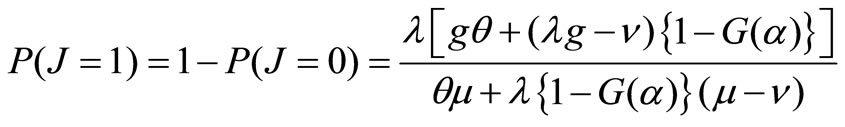
4. Stationary Waiting Time
In this Section, we can obtain the LST of the stationary waiting time of an arbitrary customer. Let 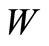 and
and 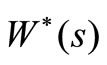 denote the stationary waiting time of an arbitrary customer and its LST, respectively.
denote the stationary waiting time of an arbitrary customer and its LST, respectively.
Theorem 2. If 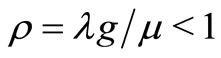 and
and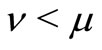 ,
, 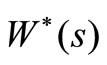 is given by
is given by
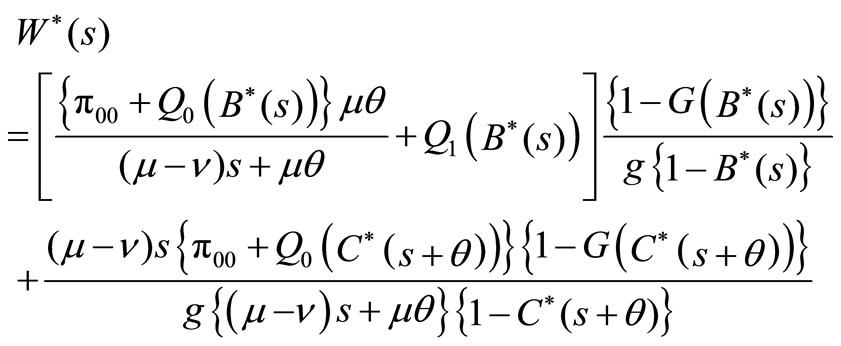 (20)
(20)
Proof: To compute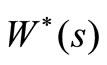 , we consider three possible cases as follows.
, we consider three possible cases as follows.
Case 1: A batch of customers including the tagged customer arrive in the state . There are
. There are 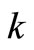 customers in front of this batch of customers in the system. In this case, a tagged customer’s waiting time in this batch is the sum of the service times of
customers in front of this batch of customers in the system. In this case, a tagged customer’s waiting time in this batch is the sum of the service times of 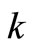 customers outside of his batch and a period of waiting time inside of his batch. Let
customers outside of his batch and a period of waiting time inside of his batch. Let 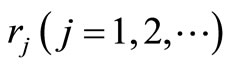 be the probability of the tagged customer being in the jth position of arriving batch. Using the result in renewal theory (Burke [12]), we have
be the probability of the tagged customer being in the jth position of arriving batch. Using the result in renewal theory (Burke [12]), we have
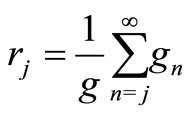
Since all the customers are served at the normal service level, the tagged customer’s waiting time conditioned that a batch of customers arrive in the state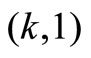 , denoted by
, denoted by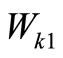 , has the LST
, has the LST
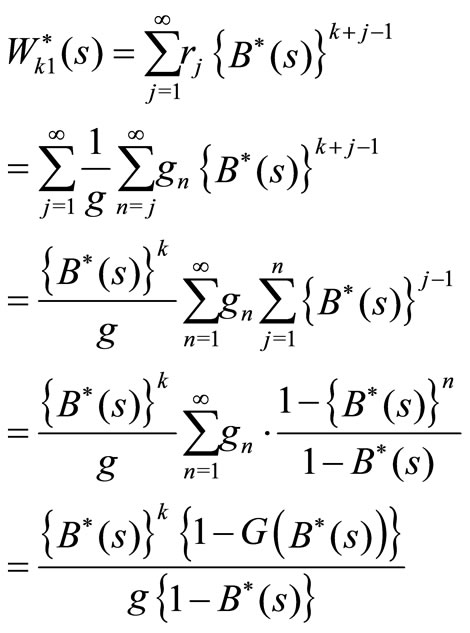
Therefore, we have
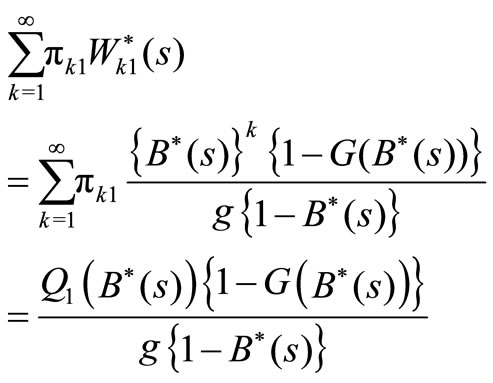 (21)
(21)
Case 2: A batch of customers including the tagged customer arrive in the state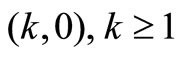 . There are
. There are 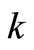 customers in front of this batch of customers in the system. If the tagged customer is the jth position in his batch, the LST of waiting time of the tagged customer is given by
customers in front of this batch of customers in the system. If the tagged customer is the jth position in his batch, the LST of waiting time of the tagged customer is given by
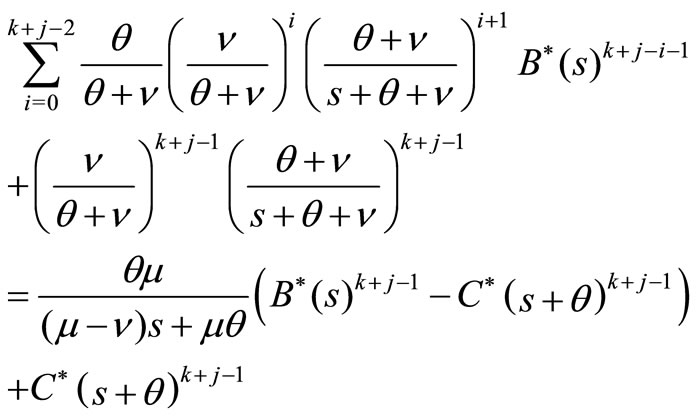
Let 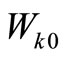 and
and  denote the tagged customer’s waiting time conditioned that a batch of customers arrive in the state
denote the tagged customer’s waiting time conditioned that a batch of customers arrive in the state 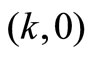 and its LST, respectively. Then we have
and its LST, respectively. Then we have
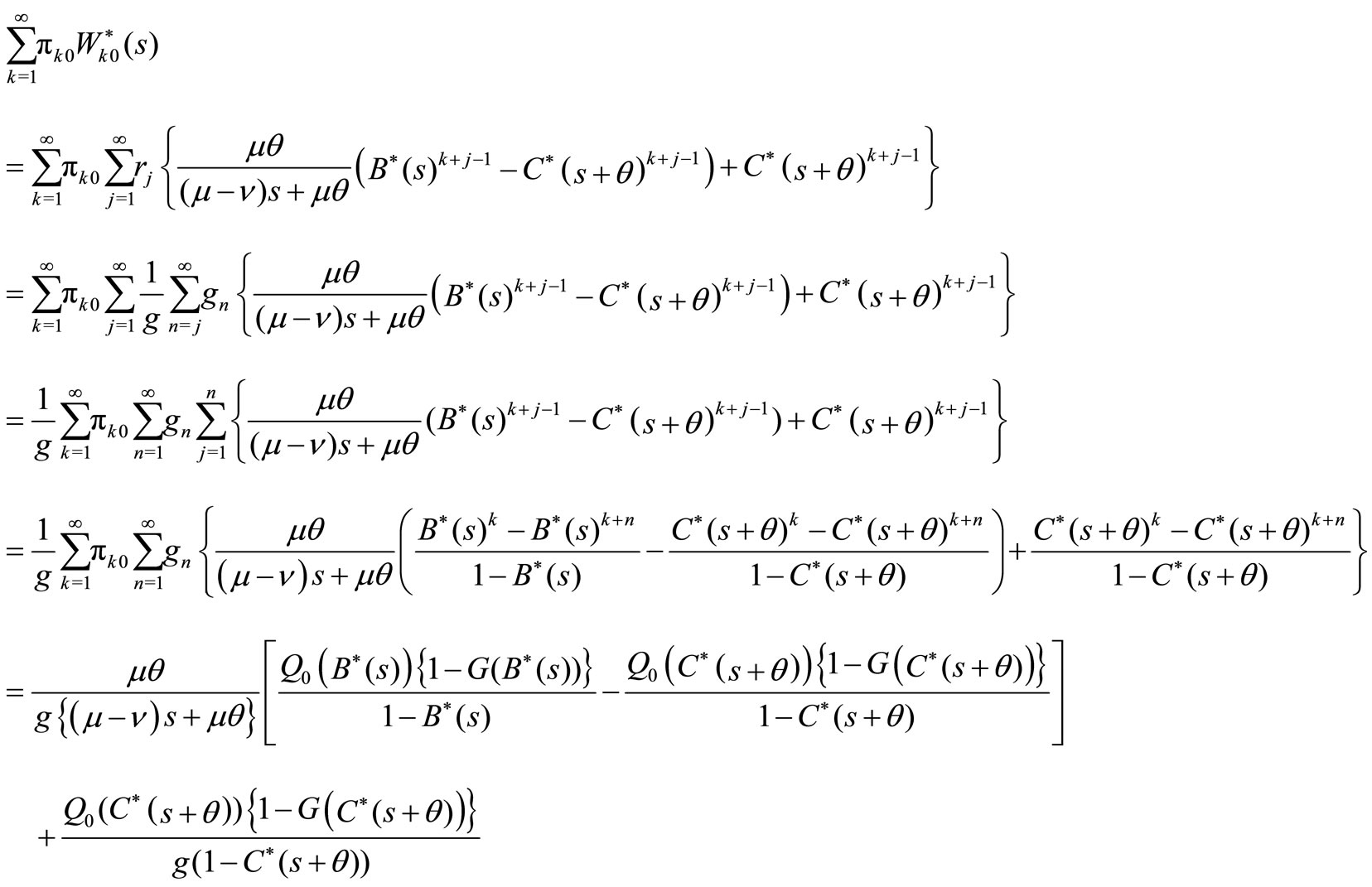 (22)
(22)
Case 3: A batch of customers including the tagged customer arrive in the state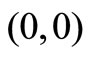 . The tagged customer’s waiting time is equal to the waiting time inside of his batch. Therefore, the tagged customer’s waiting time conditioned that a batch of customers arrive in the state
. The tagged customer’s waiting time is equal to the waiting time inside of his batch. Therefore, the tagged customer’s waiting time conditioned that a batch of customers arrive in the state , denoted by
, denoted by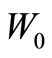 , has the LST
, has the LST

From (21), (22) and (23), we finally obtain
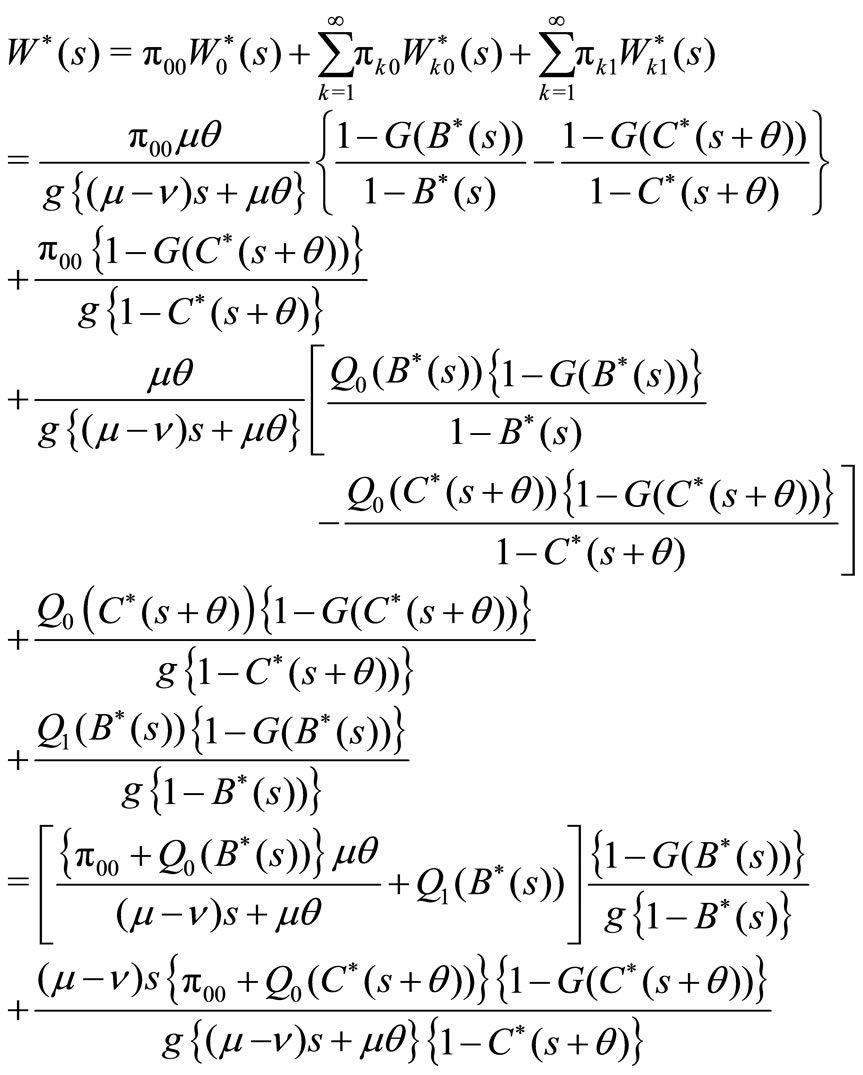
Remark 2. We can obtain the mean waiting time of an arbitrary customer, 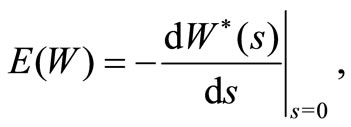 by differentiating (20) and substituting
by differentiating (20) and substituting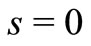 . On the other hand, the mean waiting time of an arbitrary customer,
. On the other hand, the mean waiting time of an arbitrary customer, 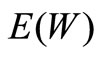 , can also be obtained by Little’s formula, that is,
, can also be obtained by Little’s formula, that is,

However, in order to obtain the higher moments of the waiting time of an arbitrary customer, 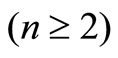
 , we must differentiate (20)
, we must differentiate (20) 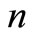 times and substitute
times and substitute 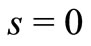 .
.
Remark 3. If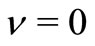 , our model reduces to a batch arrival MX/M/1 queue with multiple vacation. If the batch size of arrivals is always equal to 1, that is,
, our model reduces to a batch arrival MX/M/1 queue with multiple vacation. If the batch size of arrivals is always equal to 1, that is, 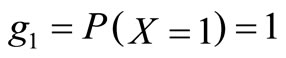 , our model reduces to an M/M/1 queue with multiple working vacation studied in Servi and Finn [4] and Liu et al. [8]. These results correspond to the known results in existing literature.
, our model reduces to an M/M/1 queue with multiple working vacation studied in Servi and Finn [4] and Liu et al. [8]. These results correspond to the known results in existing literature.
5. Numerical Results
In Section 3 and Section 4, we obtain the mean system length and the mean waiting time of an arbitrary customer. In this section, we assume that the arrival batch size 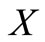 follows a geometric distribution with parameter
follows a geometric distribution with parameter , that is,
, that is, 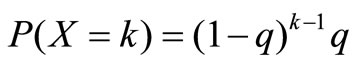
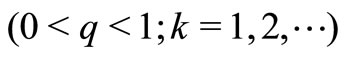 . Then it is easy to verify that
. Then it is easy to verify that
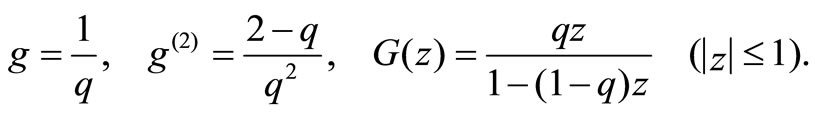
First, we consider an MX/M/1 queue with multiple working vacation where the system parameters are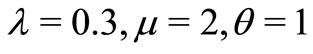 . In Figure 1, we demonstrate the effect of the service rate in the working vacation period
. In Figure 1, we demonstrate the effect of the service rate in the working vacation period  on the mean system length
on the mean system length 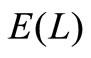 for different
for different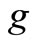 . Figure 1 indicates that
. Figure 1 indicates that 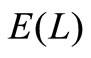 decreases as
decreases as 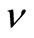 increases when
increases when 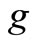 is equal to 2, 3 and 4, respectively. On the other hand, if
is equal to 2, 3 and 4, respectively. On the other hand, if  is fixed,
is fixed, 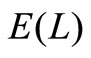 increases as
increases as 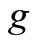 increases, that is,
increases, that is, 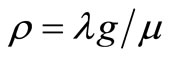 increases.
increases.
Secondly, we assume that . In Figure 2, we demonstrate the effect of
. In Figure 2, we demonstrate the effect of  on
on 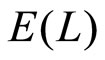 for different vacation rate
for different vacation rate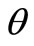 . Figure 2 indicates that
. Figure 2 indicates that 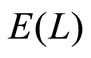 decreases as
decreases as 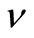 increases when
increases when 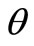 is equal to 0.5, 1.0 and 1.5, respectively. On the other hand, if
is equal to 0.5, 1.0 and 1.5, respectively. On the other hand, if 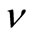 is fixed,
is fixed, 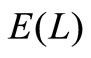 decreases as
decreases as 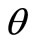 increases.
increases.
Thirdly, in Figure 3, we present the comparison of three queueing model, that is, the MX/M/1 queue without vacation, the MX/M/1 queue with multiple vacation and the MX/M/1 queue with multiple working vacation. Assume that 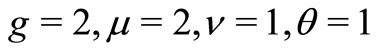 for the MX/M/1 queue with multiple working vacation. Figure 3 indicates that
for the MX/M/1 queue with multiple working vacation. Figure 3 indicates that 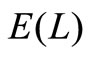 and
and 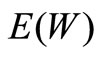 increase as
increase as 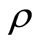 increases. On the other hand,
increases. On the other hand, 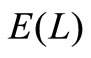 and
and 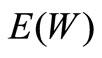 of MX/M/1 queue
of MX/M/1 queue
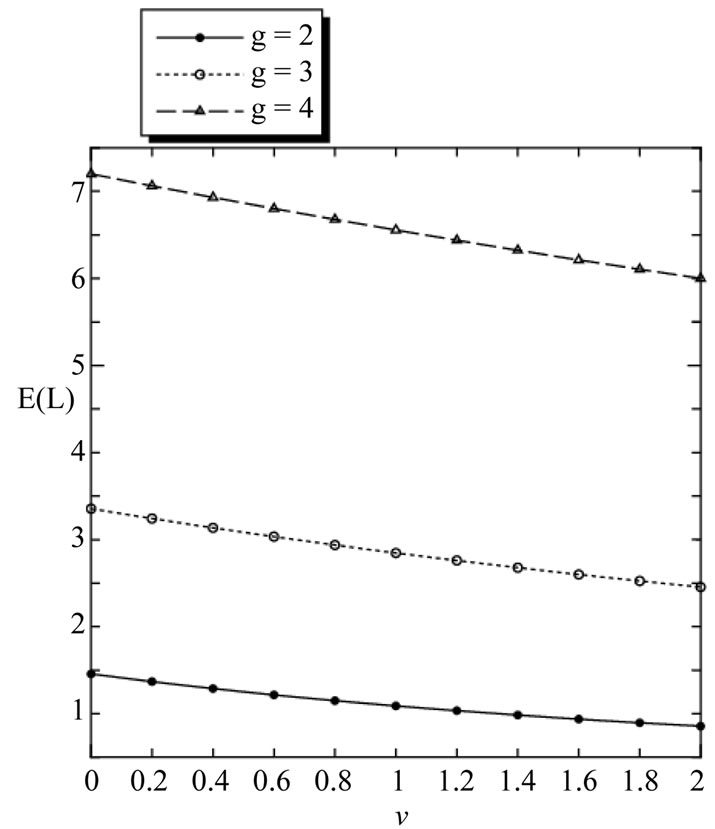
Figure 1. E(L) versus v for different g.
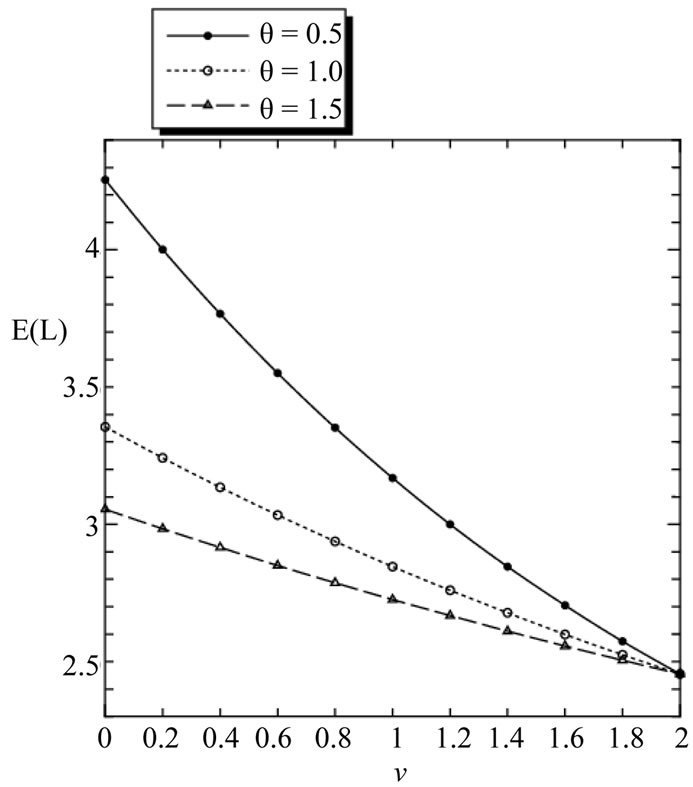
Figure 2. E(L) versus v for different θ.
without vacation are shortest and those of the MX/M/1 queue with multiple vacation are longest, which is identical with the intuition. Furthermore, Figure 3 indicates that 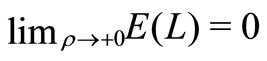 and
and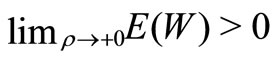 , which is a well known result for batch arrival queues.
, which is a well known result for batch arrival queues.
6. Conclusion
This paper studied the MX/M/1queue with multiple working vacation. We obtained the PGF of the stationary system length distribution and the stochastic decomposition structure of system length which indicates the relationship with that of the MX/M/1 queue without vacation. Performance indices such as the mean of stationary system length, the probability that the system is
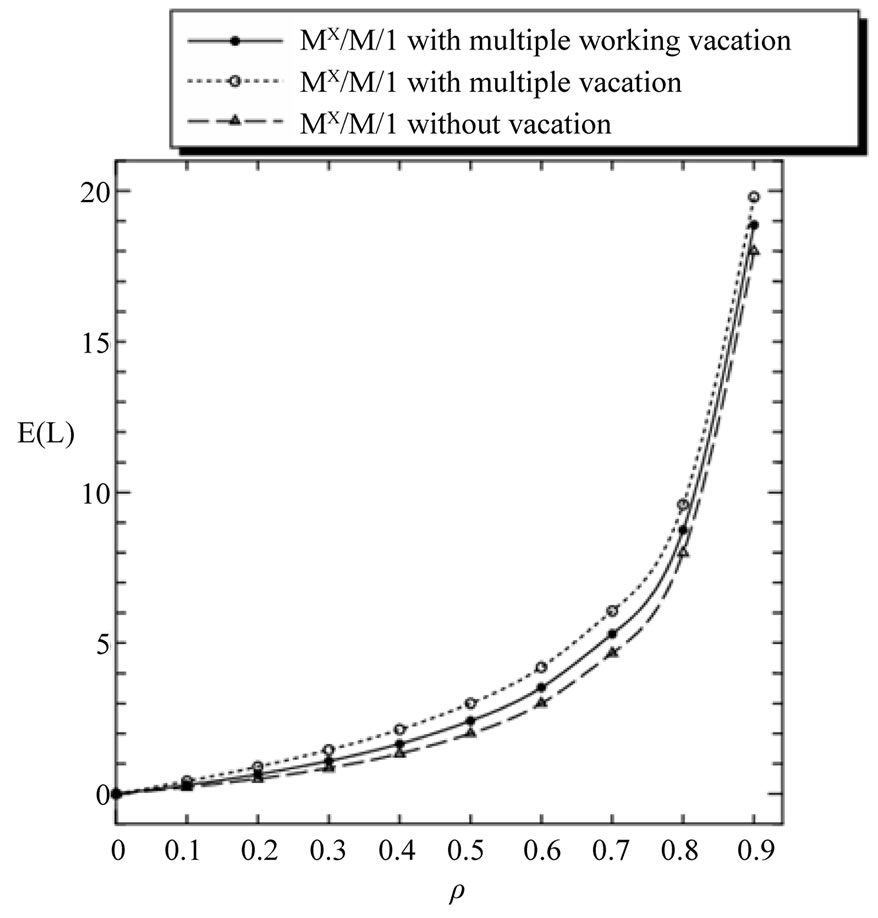
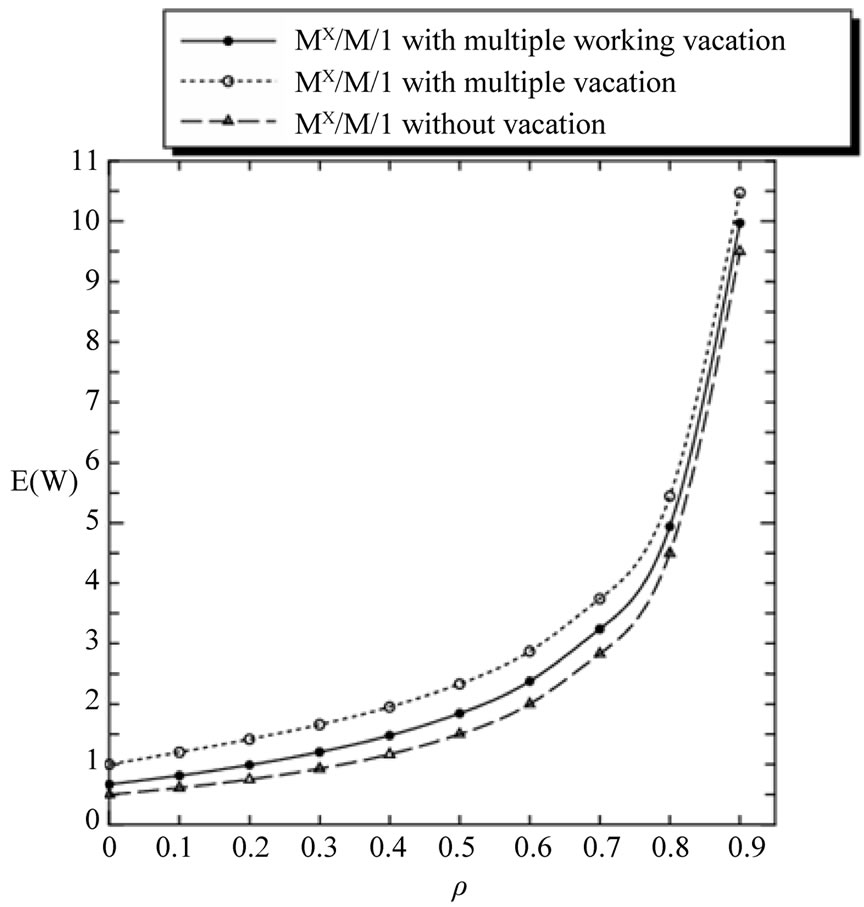
Figure 3. E(L) and E(W) versus ρ for different queueing model.
in a working vacation period and the probability that the system is in a regular busy period were also presented. Further, we obtained the LST of the stationary waiting time distribution of anarbitrary customer.We obtained the mean system length and the mean waiting time. Some numerical results for special cases showed efficiency of service in this multi-purpose batch arrival model.
7. Acknowledgements
We would like to thank the referees for valuable comments.
REFERENCES
- H. Takagi, “Queueing Analysis: A Foundation of Performance Evaluation, Vol. 1: Vacation and Priority Systems, Part 1,” Elsevier Science Publishers, Amsterdam, 1991.
- N. Tianand and G. Zhang, “Vacation Queueing ModelsTheory and Applications,” Springer-Verlag, New York, 2006.
- B. Doshi, “Queueing Systems with Vacations—A Survey,” Queueing Systems, Vol. 1, No. 1, 1986, pp. 29-66. doi:10.1007/BF01149327
- L. Servi and S. Finn, “M/M/1 Queue with Working Vacations (M/M/1/WV),” Performance Evaluation, Vol. 50, No. 1, 2002, pp. 41-52. doi:10.1016/S0166-5316(02)00057-3
- D. Wuand and H. Takagi, “M/G/1 Queue with Multiple Working Vacations,” Performance Evaluation, Vol. 64, 2006, pp. 654-681.
- Y. Baba, “Analysis of a GI/M/1 Queue with Multiple Working Vacations,” Operations Research Letters, Vol. 33, No. 2, 2005, pp. 201-209. doi:10.1016/j.orl.2004.05.006
- A. Banik, U. Gupta and S. Pathak, “On the GI/M/1/N Queue with Multiple Working Vacations-Analytic Analysis and Computation,” Applied Mathematical Modelling, Vol. 31, No. 9, 2007, pp. 1701-1710. doi:10.1016/j.apm.2006.05.010
- W. Liu, X. Xu and N. Tian, “Some Results on the M/M/1 Queue with Working Vacations,” Operations Research Letters, Vol. 35, No. 5, 2007, pp. 595-600. doi:10.1016/j.orl.2006.12.007
- J. Li, N. Tian, Z. G. Zhang and H. P. Lu, “Analysis of the M/G/1 Queue with Exponential Working Vacations-A Matrix Analytic Approach,” Queueing Systems, Vol. 61, No. 2-3, 2009, pp. 139-166. doi:10.1007/s11134-008-9103-8
- X. Xu, Z. Zhang and N. Tian, “Analysis for the M[X]/M/1 Working Vacation Queue,” International Journal of Information and Management Sciences, Vol. 20, 2009, pp. 379-394.
- M. F. Neuts, “Structured Stochastic Matrices of M/G/1 Type and Their Applications,” MarcelDekker Inc., New York, 1989.
- P. J. Burke, “Delay in Single-Server Queues with Batch Arrivals,” Operations Research, Vol. 23, No. 4, 1975, pp. 830-833. doi:10.1287/opre.23.4.830

