Applied Mathematics, 2011, 2, 1425-1431
doi:10.4236/am.2011.212201 Published Online December 2011 (http://www.SciRP.org/journal/am)
The Physical Transient Spectrum for a Multi-Photon
V-Type Three-Level Atom Interacting with a Squeezed
Coherent Field in the Presence of Nonlinearities
Fahmy K. Faramawy1, Abd El-Hameed Abd-Riheem Eied2
1Mathematics Department, Faculty of Science, Al-Azhar University, Cairo, Egypt
2Department of Mat hem at i cs, Faculty of Science, Shaqra University, Shaqra, Saudi Arabia
Received May 24, 2011; revised June 22, 2011; accepted July 1, 2011
Abstract
We study the interaction of a multi-photon three-level atom with a single mode field in a cavity, taking ex-
plicitly into account the existence of forms of nonlinearities of both the field and the intensity-dependent
atom-field coupling. The analytical forms of the emission spectrum is calculated using the dressed states of
the system. The effects of photon multiplicities, mean photon number, detuning, Kerr-like medium and the
intensity-dependent coupling functional on the emission spectrum are analyzed.
Keywords: Emission Spectrum, Nonlinearities, Multi-Photon Process
1. Introduction
The spectrum of spontaneous emission of a V-confi-
guration three-level atom, whose two upper levels are
coupled by a classical field and their energy spacing is
much larger than the spontaneous emission widths has
been investigated [1]. It has been shown that the spon-
taneously generated interference can induce the spectrum
to exhibit six peaks and depend on the phase of the
classical field. The effects of a broadband squeezed
vacuum on three-level atoms at different configurations
(, and configurations) have also been inves-
tigated [2-5]. Further work has also been done to study
the resonance fluorescence spectra of three-level atoms
interacting with two coherent lasers and two independent
squeezed vacuum [3-5]. The fluorescence spectrum for a
strongly driven three-level system in which one of the
two photon transition is coupled to a finite-bandwidth
squeezed vacuum field has been examined [4]. Quantum
interference effects in resonance fluorescence and ab-
sorption spectra of a V-type three-level atom damped by
a broadband squeezed vacuum, studied in [6].
V
In recent years, there has been tremendous progress in
the ability to generate states of the electromagnetic field
with manifestly quantum or nonclassical characteristics
experimentally [7-9]. Squeezed states of light are non-
classical states for which the fluctuations in one of two
quadrature phase amplitudes of the electromagnetic field
drop below the level of fluctuations associated with the
vacuum state of the field. Squeezed states therefore pro-
vide a field which is in some sense quieter than the va-
cuum state and hence can be employed to improve mea-
surement precision beyond the standard quantum limits.
The goal of this paper is to shed some light on the
emission spectrum for a general three-level system. The
model we shall consider is consisting of a single V-type
three level atom interacting with a multi-photon one
mode field in a perfect cavity, including acceptable kinds
of nonlinearities of both the field and the intensity-
dependent atom-field coupling. To reach our goal it is
more convenient to use exact expression for the unitary
operator in the frame of the dressed state for-
malism. This will be considered in Section 2. In Section
3 we employ the analytical results obtained to find an
analytical expression for the emission spectrum by using
the finite double-Fourier transform of the two-time field
correlation function. By a numerical computation, we
examine the influence of photon multiplicities, mean
photon number, detuning parameters,the functional de-
pendence of the coupling as well as the nonlinearity pa-
rameter on the emission spectrum in Section 4. Finally
the conclusions are summarized in Section 5.
()Ut
2. Formulation of the Problem
The Hamiltonian of the system in the rotating-wave app-

F. K. FARAMAWY ET AL. 1426
roximation is of the form (=1)
0
=in
H
HH

(1)
3
0,
=1
ˆˆ
=jjj
j
H
aa 




(2)
The operators and are the boson operators for
the field satisfying . Where
ˆ
aˆ
a
]=

ˆˆ
[, 1aa 12 ,

 and 3

are the atomic levels energies 123
(> )>

 and

is the field frequency, with the detuning parameters 1

and (as shown in Figure 1) given by
2

1132 2
=(),=(kk
3
)

    (3)
The interaction part of the Hamiltonian in the presence
of an arbitrary nonlinear medium, via multi-photon pro-
cess can be written as k


†††
11311 31
††
22322 32
ˆˆˆˆˆˆˆˆ
=( )( )( )
ˆˆˆ ˆˆˆ
()() .
kk
in
kk
Haa faaaafaa
f aaaaf aa


 


 
 (4)
†
ˆˆ
(aa)) and †
ˆˆ
(
f
aa are Hermitian operators func-
tions of photon number operators, such that †
11 ˆˆ
()
f
aa 
and †
ˆˆ
(
22 )
f
aa
ij
 represents an arbitrary intensity-de-
pendent atom-field coupling, while denotes the
one-mode field nonlinearity which can model Kerr-like
medium nonlinearity as will be discussed later. The
operators
†
ˆˆ
(aa)

satisfy the following commutation rela-
tions [,
ij ] l= il j  j il 

   , ˆ a[, ]=0
ij

.
The initial state (0)AF of the combined atom-field
system may be written as
(0)=(0)(0)
AFA F
 (5)
where (0)= 11
A
 the initial state of the atom and
(0) =
F
 is the initial state of the field. The
initial state () =n pn where the probability am-
plitude is defined in the usual manner as
)( n
p
=|
n
pn.
The time evolution between the atom and the field is
defined by the unitary evolution operator generated by
H
. Thus is given by: ()Ut


() exp.Ut iHt
This unitary operator is written as ()Ut
1()() ()
03
=0
3()() ()
==1
()= exp()
exp( )
ksss
s
nnn
jjj
nkj
UtiE t
iE t






(6)
where j = 1, 2, 3 and the eigenvalues
()
03 3
=(),(= 0,1,,1)
s
Esssk   
Figure 1. Energy level diagram for a V-type three-level
atom with k-photon detuning Δ1, Δ2.


() 2 1
12
2
=3
33
ncos()
j
j
X
EXX

  (7)
and

3
12 13 1
3
22
12
9227
12π
=(
cos
33
23
j
XX XXj
XX






 




 


1), (8)
with
1123
22
212121323
22
32112123
11
22
33
1112 22
=( )
=
=
=()
=()
=()()
()! ()
=(),= ()
!!
Xrrr
XVVrrrrrr
XrVrVrrr
rnn
rnn
rnknk
nk nk
VfnV fn
nn




!






 
 
 

(9)
and ()s ,

n
j
 are the dressed states of the system
associated with the eigenvalues ()
03
s
E and (j = 1,
2, 3).
()
,
n
j
E
() =,3,(=0,1, ,1) sssk


() ()()()
=,1 ,2,
nn n n
jj jj
nn n  3k (10)
where



()
() 12
() ()
21
() () ()
12
1
=
n
nj
j
n nj
j
nnn
jjj
Vr E
Vr E
M
rE rE





 
 
 
 

 
 
 
 



(11)

F. K. FARAMAWY ET AL.1427
()2()22()22()
12 1221
=
()()()(
nn n
jjj j
M
rErE VrEVrE
2
)
n
(12)
Having obtained the explicit form of the unitary
operator , the eigenvalues and the eigenfunctions
for the system under consideration, we are therefore in a
position to discuss any property related to the atom or the
field.
()Ut
3. The Physical Transient Spectrum
In this section we derive the physical transient spectrum
()S

by calculating the Fourier transform of the time
averaged dipole-dipole correlation function
 
13 1231312322
()()()()tttt  , The physical spe-
ctrum ()S

of radiation field emitted by a cavity-bound
atom is given by the expression [10].

 

121 2
00
13 1231312322
()=dd exp()()()()
() ()() ().
TT
Stt iTtiT
tttt


 
 
 t

(13)
where is the interaction time and  is the band-
width of the filter. After carrying out the various ope-
rations we get
T
13 22
()()() ()
03
=0 =1
2
()*()()() *()()
33 22 2
()()()() ()
==1=1
22
()*() ()()*()()
()=( ,)
(,
kssss
jj
sj
ssssss
jjjjjj
nnnknk n
jiij
nki j
nnnnnn
jjjjjj
SpEE
pE











 

 




2
)E





(14)
where
22
1exp(2 )2exp()cos()
(, )=()
TTx
xy xy



yT
 

 




(15)
Thus the time averaged spectrum consists of resonant
structures which arise from transitions among different
dressed states. The final structure of the time averaged
spectrum will depend on the form of the input photon
distribution p(n). Due to the quantum interference be-
tween component states the oscillations in the cavity
field become composed of different component states.
4. Results and Discussion
On the basis of the analytical solution presented in a
previous section, we shall study numerically the physical
transient spectrum in a a squeezed coherent initial field.
The photon number distribution for a squeezed coherent
state [11] can be written as
2
2
22
(tanh )
=2!cosh 2cosh sinh
exptanh( ),
n
nn
n
r
Ps H
nr rr
rRe








(16)
where, =coshsinh, =exp()rr i




 and Hn
is the Hermite polynomial. We suppose here the minor
axis of the ellipse, representing the direction of squeez-
ing, parallel to the coordinate of the field oscillator. The
initial phase

of

is the angle between the dire-
ction of coherent excitation and the direction of squeez-
ing. The mean photon number of this field is equal to
22
=.nr
sinh
  Putting we get the photon dis-
tribution for an initial coherent state with
=0r2
=n

whereas for =0

the photon distribution for an initial
squeezed vacuum state with 2 =sinhnr is recovered.
The latter distribution is oscillatory with zeros for odd
. n
By means of dressed atom states, and quantum beats
we know that when the number changes by unit,
this coupling describes the spontaneous emission of
photon with a frequency close to . Since the dressed
nkk

state ()
3
nk
 is totally decoupled from the other dre-
ssed states, it can not be populated [12,13]. Then the
field can only couple such transitions where the final sta-
tes are either 1

or 2

but not 3  [12,14]. So,
there are only six possible allowed spontaneous decays
from the three perturbed states of (where
()n
E


()() () ()
123
=,,
n nnn
E) to lower multiplicities
()nk
j
E

[15,16]. Generally they are asymmetric, because
the intensities of the symmetrically placed sidebands are
not equal. While at exact resonance the spectrum be-
comes symmetric [16]. Due to the non population of the
dressed state 3

the two transitions 31


and 32

 vanish [12-14]. Hence, the emission
spectrum of -type three-level atom for a single cavity
field has four-peak structure. In what follows we shall
consider the effect of men photon number, detuning
parameters 12
V
,

, intensity dependent coupling ()
i
f
n
and the nonlinear Kerr medium parameter

on the
spectrum of the system under consideration.
4.1. Effect of Multiplicity and Mean Photon
Number
For small = 1kn Rabi vacuum peaks dominate the
spectrum see Figure 2.1(a). While by increasing the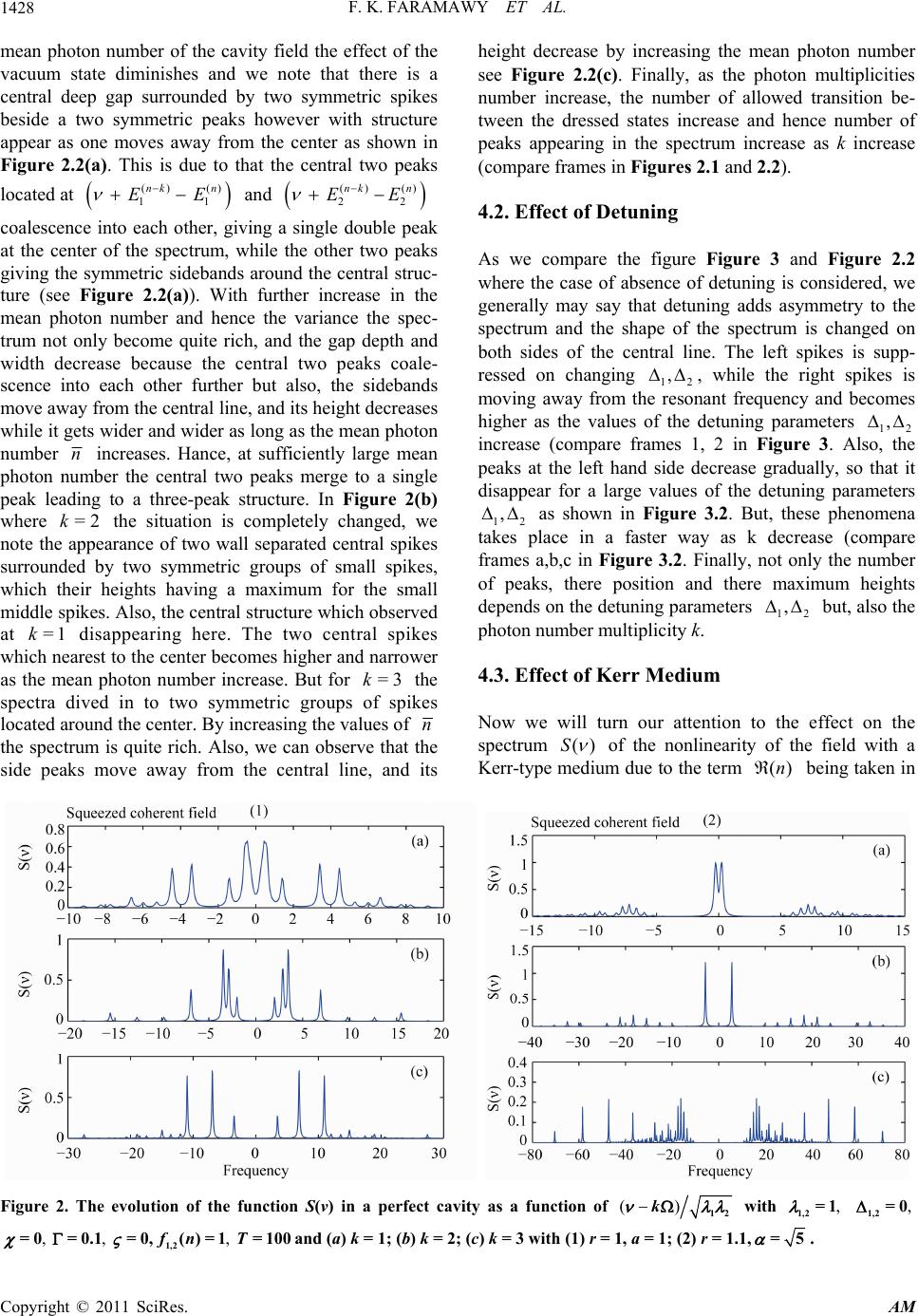

F. K. FARAMAWY ET AL. 1428
mean photon number of the cavity field the effect of the
vacuum state diminishes and we note that there is a
central deep gap surrounded by two symmetric spikes
beside a two symmetric peaks however with structure
appear as one moves away from the center as shown in
Figure 2.2(a). This is due to that the central two peaks
located at and

() ()
11
nk n
EE 



() ()
22
nk n
EE 


height decrease by increasing the mean photon number
see Figure 2.2(c). Finally, as the photon multiplicities
number increase, the number of allowed transition be-
tween the dressed states increase and hence number of
peaks appearing in the spectrum increase as k increase
(compare frames in Figures 2.1 and 2.2).
4.2. Effect of Detuning
coalescence into each other, giving a single double peak
at the center of the spectrum, while the other two peaks
giving the symmetric sidebands around the central struc-
ture (see Figure 2.2(a)). With further increase in the
mean photon number and hence the variance the spec-
trum not only become quite rich, and the gap depth and
width decrease because the central two peaks coale-
scence into each other further but also, the sidebands
move away from the central line, and its height decreases
while it gets wider and wider as long as the mean photon
number n increases. Hance, at sufficiently large mean
photon number the central two peaks merge to a single
peak leading to a three-peak structure. In Figure 2(b)
where the situation is completely changed, we
note the appearance of two wall separated central spikes
surrounded by two symmetric groups of small spikes,
which their heights having a maximum for the small
middle spikes. Also, the central structure which observed
at disappearing here. The two central spikes
which nearest to the center becomes higher and narrower
as the mean photon number increase. But for the
spectra dived in to two symmetric groups of spikes
located around the center. By increasing the values of
=2k
=1k
=3k
n
the spectrum is quite rich. Also, we can observe that the
side peaks move away from the central line, and its
As we compare the figure Figure 3 and Figure 2.2
where the case of absence of detuning is considered, we
generally may say that detuning adds asymmetry to the
spectrum and the shape of the spectrum is changed on
both sides of the central line. The left spikes is supp-
ressed on changing 12
,

, while the right spikes is
moving away from the resonant frequency and becomes
higher as the values of the detuning parameters 12 ,


increase (compare frames 1, 2 in Figure 3. Also, the
peaks at the left hand side decrease gradually, so that it
disappear for a large values of the detuning parameters
12
,

 as shown in Figure 3.2. But, these phenomena
takes place in a faster way as k decrease (compare
frames a,b,c in Figure 3.2. Finally, not only the number
of peaks, there position and there maximum heights
depends on the detuning parameters but, also the
photon number multiplicity k.
12
,
4.3. Effect of Kerr Medium
Now we will turn our attention to the effect on the
spectrum ()S

of the nonlinearity of the field with a
Kerr-type medium due to the term being taken in
()n
Figure 2. The evolution of the function S(v) in a perfect cavity as a function of ()12

 k with ,
1,2 =1

,
1,2 =0

, , ,
1,2
=0=0.1=0,()=1=100

 fn Tand (a) k = 1; (b) k = 2; (c) k = 3 with (1) r = 1, a = 1; (2) r = 1.1,=5  .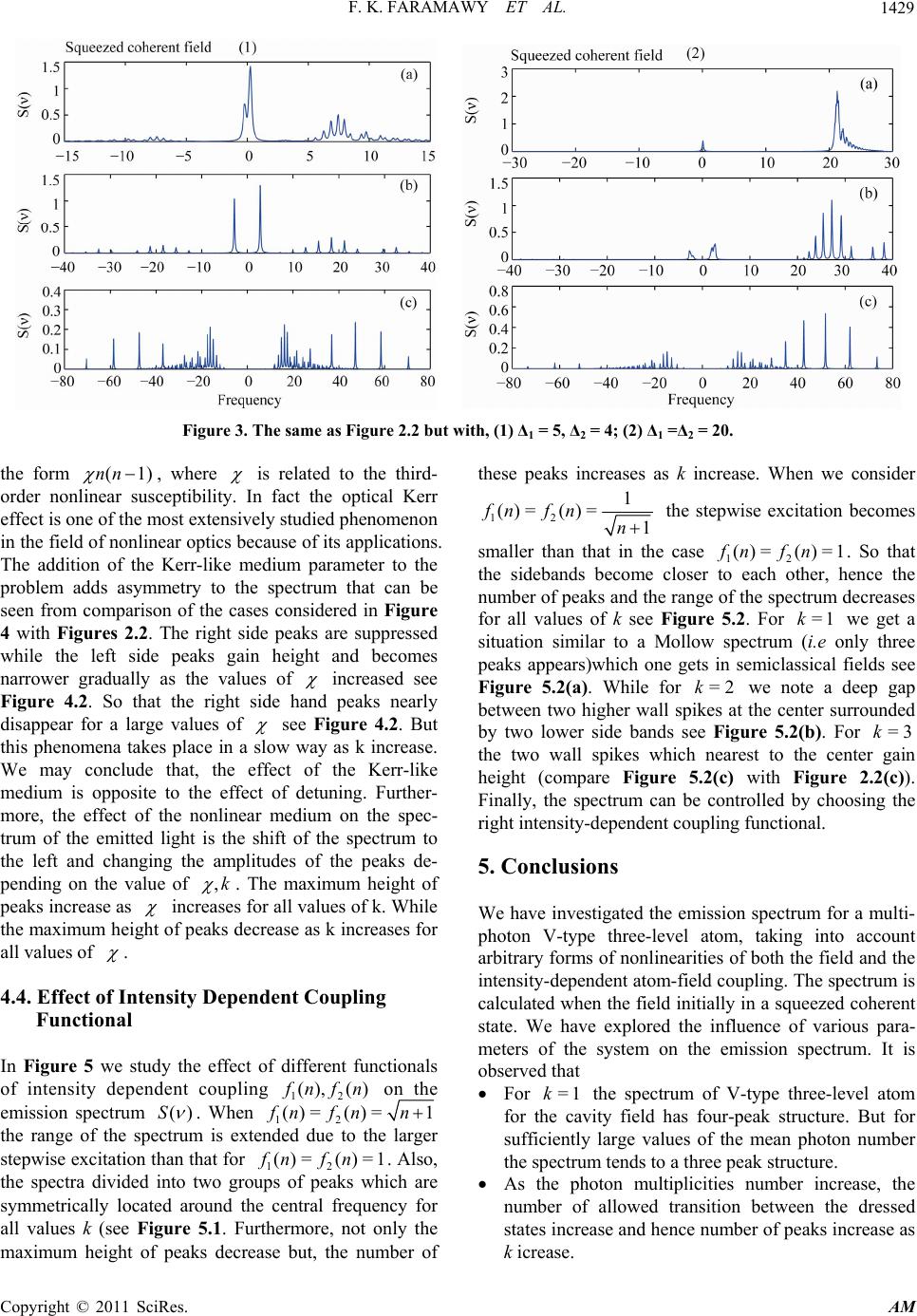

F. K. FARAMAWY ET AL.1429
Figure 3. The same as Figure 2.2 but with, (1) Δ1 = 5, Δ2 = 4; (2) Δ1 =Δ2 = 20.
the form (1)nn

, where

is related to the third-
order nonlinear susceptibility. In fact the optical Kerr
effect is one of the most extensively studied phenomenon
in the field of nonlinear optics because of its applications.
The addition of the Kerr-like medium parameter to the
problem adds asymmetry to the spectrum that can be
seen from comparison of the cases considered in Figure
4 with Figures 2.2. The right side peaks are suppressed
while the left side peaks gain height and becomes
narrower gradually as the values of

increased see
Figure 4.2. So that the right side hand peaks nearly
disappear for a large values of

see Figure 4.2. But
this phenomena takes place in a slow way as k increase.
We may conclude that, the effect of the Kerr-like
medium is opposite to the effect of detuning. Further-
more, the effect of the nonlinear medium on the spec-
trum of the emitted light is the shift of the spectrum to
the left and changing the amplitudes of the peaks de-
pending on the value of ,k

. The maximum height of
peaks increase as

increases for all values of k. While
the maximum height of peaks decrease as k increases for
all values of

.
4.4. Effect of Intensity Dependent Coupling
Functional
In Figure 5 we study the effect of different functionals
of intensity dependent coupling 12
(), ()
f
nfn on the
emission spectrum ()S

. When 12 ()= ()
these peaks increases as k increase. When we consider
12
1
()=()=1 fn fnn

the stepwise excitation becomes
smaller than that in the case 12. So that
the sidebands become closer to each other, hence the
number of peaks and the range of the spectrum decreases
for all values of k see Figure 5.2. For we get a
situation similar to a Mollow spectrum (i.e only three
peaks appears)which one gets in semiclassical fields see
Figure 5.2(a). While for we note a deep gap
between two higher wall spikes at the center surrounded
by two lower side bands see Figure 5.2(b). For
the two wall spikes which nearest to the center gain
height (compare Figure 5.2(c) with Figure 2.2(c)).
Finally, the spectrum can be controlled by choosing the
right intensity-dependent coupling functional.
()= ()=1fn fn
=1k
=2k
=3k
5. Conclusions
We have investigated the emission spectrum for a multi-
photon V-type three-level atom, taking into account
arbitrary forms of nonlinearities of both the field and the
intensity-dependent atom-field coupling. The spectrum is
calculated when the field initially in a squeezed coherent
state. We have explored the influence of various para-
meters of the system on the emission spectrum. It is
observed that
 For =1k the spectrum of V-type three-level atom
for the cavity field has four-peak structure. But for
sufficiently large values of the mean photon number
the spectrum tends to a three peak structure.
= 1
f
nfn n

the range of the spectrum is extended due to the larger
stepwise excitation than that for 12. Also,
the spectra divided into two groups of peaks which are
symmetrically located around the central frequency for
all values k (see Figure 5.1. Furthermore, not only the
maximum height of peaks decrease but, the number of
()=()=fnfn1
 As the photon multiplicities number increase, the
number of allowed transition between the dressed
states increase and hence number of peaks increase as
k icrease.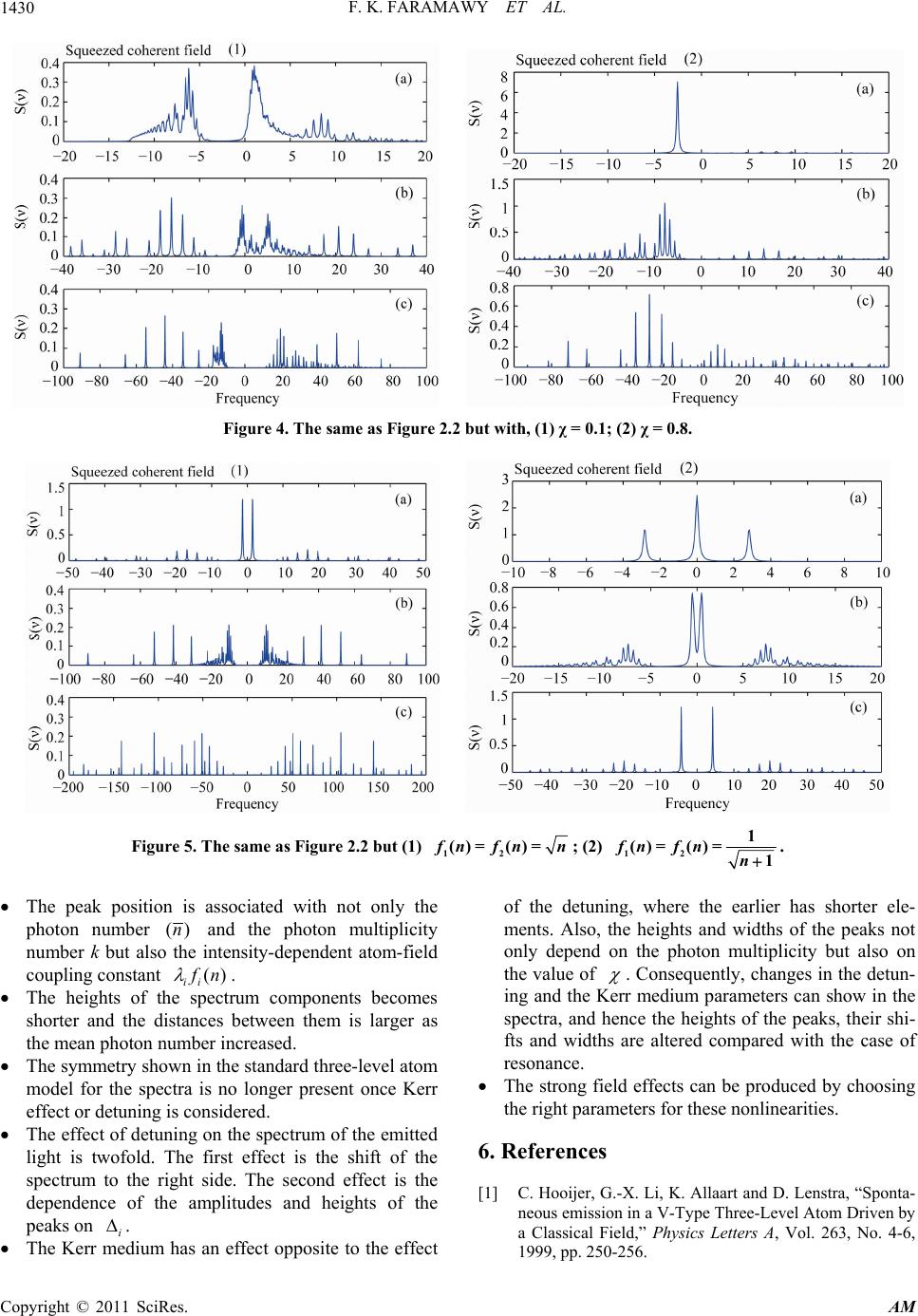

F. K. FARAMAWY ET AL. 1430
Figure 4. The same as Figure 2.2 but with, (1) χ = 0.1; (2) χ = 0.8.
Figure 5. The same as Figure 2.2 but (1) 12 ()=()=
f
n
f
nn; (2) 12
1
()=()=1 fn fnn.
 The peak position is associated with not only the
photon number ()n and the photon multiplicity
number k but also the intensity-dependent atom-field
coupling constant ()fn
ii

.
 The heights of the spectrum components becomes
shorter and the distances between them is larger as
the mean photon number increased.
 The symmetry shown in the standard three-level atom
model for the spectra is no longer present once Kerr
effect or detuning is considered.
 The effect of detuning on the spectrum of the emitted
light is twofold. The first effect is the shift of the
spectrum to the right side. The second effect is the
dependence of the amplitudes and heights of the
peaks on .
i
 The Kerr medium has an effect opposite to the effect
of the detuning, where the earlier has shorter ele-
ments. Also, the heights and widths of the peaks not
only depend on the photon multiplicity but also on
the value of

. Consequently, changes in the detun-
ing and the Kerr medium parameters can show in the
spectra, and hence the heights of the peaks, their shi-
fts and widths are altered compared with the case of
resonance.
 The strong field effects can be produced by choosing
the right parameters for these nonlinearities.
6. References
[1] C. Hooijer, G.-X. Li, K. Allaart and D. Lenstra, “Sponta-
neous emission in a V-Type Three-Level Atom Driven by
a Classical Field,” Physics Letters A, Vol. 263, No. 4-6,
1999, pp. 250-256.

F. K. FARAMAWY ET AL.1431
doi:10.1016/S0375-9601(99)00718-5
[2] Z. Ficek and P. D. Drummond, “Three-Level Atom in a
Broadband Squeezed Vacuum Field. I. General Theory,”
Physical Review A, Vol. 43, No. 11, 1991, pp. 6247-6257.
doi:10.1103/PhysRevA.43.6247
[3] S. Smart and S. Swain, “Three-Level Atom in a Squeezed
Vacuum II. Resonance Fluorescence,” Journal of Modern
Optics, Vol. 41, No. 6, 1994, pp. 1055-1077.
doi:10.1080/09500349414551021
[4] B. J. Dalton, M. R. Ferguson and Z. Ficek, “Resonance
Fluorescence Spectra of Three-Level Atoms in a
Squeezed Vacuum,” Physical Review A, Vol. 54, No. 3,
1996, pp. 2379-2390. doi:10.1103/PhysRevA.54.2379
[5] B. J. Dalton M. Bostick and Z. Fizec, “Probe Absorption
Spectra for Driven Atomic Systems in a Narrow Band-
width Squeezed Vacuum,” Physical Review A, Vol. 53,
No. 6, 1996, pp. 4439-4439.
doi:10.1103/PhysRevA.53.4439
[6] O. G. Calderon, F. Carreno and M. A. Anton, “Quantum
Interference Effects in Resonance Fluorescence and Ab-
sorption Spectra of a-Type Three-Level Atom Damped
by a Broadband Squeezed Vacuum,” Optics Communica-
tions, Vol. 221, No. 4-6, 2003, pp. 365-385.
doi:10.1016/S0030-4018(03)01490-1
[7] D. F. Walls and G. J. Milburn, “Quantum Optics,” Sprin-
ger-Verlag, Berlin, 1994.
[8] C. M. Caves and B. L. Schumaker, “New Formalism for
Two-Photon Quantum Optics. I. Quadrature Phase and
Squeezed States,” Physical Review A, Vol. 31, No. 5,
1985, pp. 3068-3092. doi:10.1103/PhysRevA.31.3068
[9] V. V. Dodonov, “Nonclassical States in Quantum Optics:
A Squeezed Review of the First 75 Years,” Journal of
Optics B, Vol. 4, No. 1, 2002, p. R1.
doi:10.1088/1464-4266/4/1/201
[10] J. H. Eberly and K. Wodkiewicz, “The Time-Dependent
Physical Spectrum of Light,” Journal of the Optical Soci-
ety of America, Vol. 67, No. 9, 1977, pp. 1252-1261.
doi:10.1364/JOSA.67.001252
[11] R. Loudon, “Quantum Statistics of Linear and Nonlinear
Optical Phenomena,” Optica Acta: International Journal
of Optics, Vol. 31, No. 8, 1984, pp. 847-852.
doi:10.1080/713821593
[12] S.-Y. Zhu, R. C. F. Chan and C. P. Lee, “Spontaneous
Emission from a Three-Level Atom,” Physical Review A,
Vol. 52, No. 1, 1995, pp. 710-716.
doi:10.1103/PhysRevA.52.710
[13] G. X. Li, K. Allaart, C. Hooijer and D. Lenstra, “Sponta-
neous Emission in a V-Type Three-Level Atom Driven
by a Classical Field,” Physics Letters A, Vol. 263, No.
4-6, 1999, pp. 250-256.
doi:10.1016/S0375-9601(99)00718-5
[14] P. Dong and S. H. Tang, “Absorption Spectrum of a
V-Type Three-Level Atom Driven by a Coherent Field,”
Physical Review A, Vol. 65, 2002, Article ID 033816, 10
Pages.
[15] C. Cohen-Tannoudji and S. Reynaud, “Dressed-Atom
Description of Resonance Fluorescence and Absorption
Spectra of a Multi-Level Atom in an Intense Laser
Beam,” Journal of Physics B, Vol. 10, No. 3, 1977, p.
345. doi:10.1088/0022-3700/10/3/005
[16] C. Cohen-Tannoudji and S. Reynaud, “Simultaneous
Saturation of Two Atomic Transitions Sharing a Com-
mon Level,” Journal of Physics B, Vol. 10, No. 12, 1977,
p. 2311. doi:10.1088/0022-3700/10/12/010