 Journal of Software Engineering and Applications, 2011, 4, 672-681 doi:10.4 23 6/jse a .20 11 .4 12 07 9 Pu blishe d Onli ne December 2011 (http://www.SciRP.org/journal/jsea) Cop yright © 2011 Sci Res. JSEA Modelling and Wavelet-Based Identification of 3-DOF Vehicle Suspension System Khaled Nouri, Hichem Loussifi, Naceur Benhadj Braiek Laboratoire d’Etude et Commande Automatique des Processus (LECAP), Ecole Polytechnique de Tunisie, Université de Carthage, Tunis, Tunisia. Email: {khaled.nouri, naceur.benhadj}@ept.rnu.t n, hichem.loussifi@gmail. com Received Oct ober 21st, 2011; revised November 29th, 2011; accept ed December 1 0th, 2011. ABSTRACT In this paper, a three Degrees of Freedom (DOF) model of a quarter vehicle suspension system is proposed including the seat driver mass. The modal parameters of this system, which indicate the comfort and the safety of the suspension, are identified using Wavelet analysis. Two applications of wavelet analysis are presented: signal denoising based on the Discrete Wavelet Transform (DWT) and modal identification based on the Continuous Wavelet Transform (CWT). It is shown that the CWT analysis of the system response, initially denoised using DWT, allows the estimation of the natural pulsations and the damping ratios. The usefulness of the DWT in denoising and the accuracy of the CWT in modal iden- tification are tested and confirmed by applying them to the proposed model. The complete modeling and identification of a 3-DOF vehicle suspension system is developed and the simulation results verify these statements and are satisfac- tory. Keywords: Suspension System, Discrete and Continuous Wavelet Transform, Signal Denoising, Modal Identification 1. Introduction The importance of the suspension system of a vehicle is that it is responsible of the comfort of the driver and the sa fety of the vehicle since it i s the part o f the ve hicle which carries the body of the vehicle and which transmits all the forces between this body and the road. For that, the complete physical model of the suspension is often re- duced under investigation of the vertical dynamics estab- lished on a quarter-vehicle model. The study of this model, and like any mechanical system, presents challenge for engineers and researchers. Noise reduction and parame- ters identification from system response are common pro- blems in signal processing and vibrational applications [1-3]. That’s why numerous approaches have been deve- loped recently and applied to denoise signals and to ex- tract modal parameters of systems and structures in time and frequency domains [1]. The wavelet analysis is one of these new approaches that were revealed mainly because it represents an easy way of extracting time varying frequency components. Indeed, the Wavelet Transform technique is shown to be more effective than other denoising methods such the Fourier Transform (FT) or Compressed Sensing technique [1], and more useful than other identification methods such as Hilbert-Huang Transform [4-6]. In noise reduction, wavelets has been successfully used by Giaouris et al. [2] in order to propose a new pseudo- adaptive denoising method based on the Wavelet Trans- form, this method adjust the level of signal decomposi- tion and was applied effectively to an electric drive. In systems identification, resonant pulsations and damp- ing ratios are the most difficul t quantity to deter mine and requires dynamic tests [3,4]. Numerous approaches have been developed and applied to identify modal parameters of systems and structures in time-frequency domain such as the WT [5,6] and the Hilbert-Huang Transform (HHT) [7,8]. The objective of this study is focuses first to propose a model of a quarter vehicle suspense system and then to identify the parameters of the proposed model of the con- sidered system using WT. The different sections of this paper are organized as follows: in section II a complete modeling of a 3-DOF quarter suspension system is proposed with a dynamical study followed by a Simulink diagram of the considered vehicle model. Beginning with some mathematical fun- daments of the discrete and the continuous WT, denois- ing and the identification methods are presented in section III. The simulation results are illustrated and discussed in  Modelling and Wavelet-Based Identification of 3-DOF Vehicle Suspension System673 section IV, and a conclusion is drawn in section V. 2. Proposed 3-DOF Model for the Vehicle Suspension The suspension system has a big role in design and dyna- mic of the vehicle. Indeed its goal is to maintain the com- fort of the passengers and the stability of the vehicle by supporting the weight of the vehicle, by reducing the dis- turbances of road and by avoiding the road excitations experienced by the tires from being transmitted to the pas- sengers. The suspension system is generally reduced to a quar- ter vehicle model and the majority of the suspension studies use a model with two DOF. In our study, we propose a three DOF model including the seat and drive mass ( m), chassis mass (c) and the tire mass (t). The proposed suspension system is modeled by interconnecting three mass-spring-damper systems as shown in Figure 1. m m Assuming that each sub-system is represented b y a mass connected to parallel arrangement of a linear spring and a linear viscous damper, the three DOF are the vertical mo- tions of: the seat, the chassis and the tire. The model shown in Figure 1 includes for each mass a stiffness constant k, a damping constant c and a vertical displacement z. The vertical displacement r denotes the change of road surface elevation. Assuming that the tire does not break away from the road surface and that the displacements are measured for m the static equ ilibrium positio ns, the linear equation of mo- tion for the seat mass is: 0 ss ss css c mzc zzk zz (1) Similarly, the equation of motion of the chassis mass is given as: Figure 1. Proposed 3-DOF model of a quarter-vehicle sus- pension s ystem. cc cc tcc tsscss c mzczz kzzczzkzz (2) and that of the tire mass is : ttttrt trc ctc ct mzczzkzzczzkzz (3) These three differential equations can be written in the matrix form as follows: ZZLU MDS (4) where: 00 0 00; 00 0 0 0 sss cssc tc ss ssc c cct mcc mccc mc kk kkk k kkk MD S ; c ct c cc and 00 ;00; sr cr tt t z Zz LU kc z M is the inertia matrix, D the damping matrix and S the stiffness ma trix. From these dynamical driving equations, we can de- rive the state space representation of the system by as- suming the state space variables are as follows: 1 2 3 4 5 6 c t c t xz xz xz Xxz xz xz (5) As a result, the state space representation of the pro- posed model is: XX YX AB CD U U (6) where A is the state matrix, the input matri x, C the output matrix, the transmission matrix, U the in- pu t of the sys tem and Y its outpu t . 000100 000010 000001 00 00 ss ss ss ss ssc cssc c cc ccc c cct cct tt tt kk cc mm mm kkk kccc c mm mmm m kkk ccc mm mm A Cop yright © 2011 Sci Res. JSEA 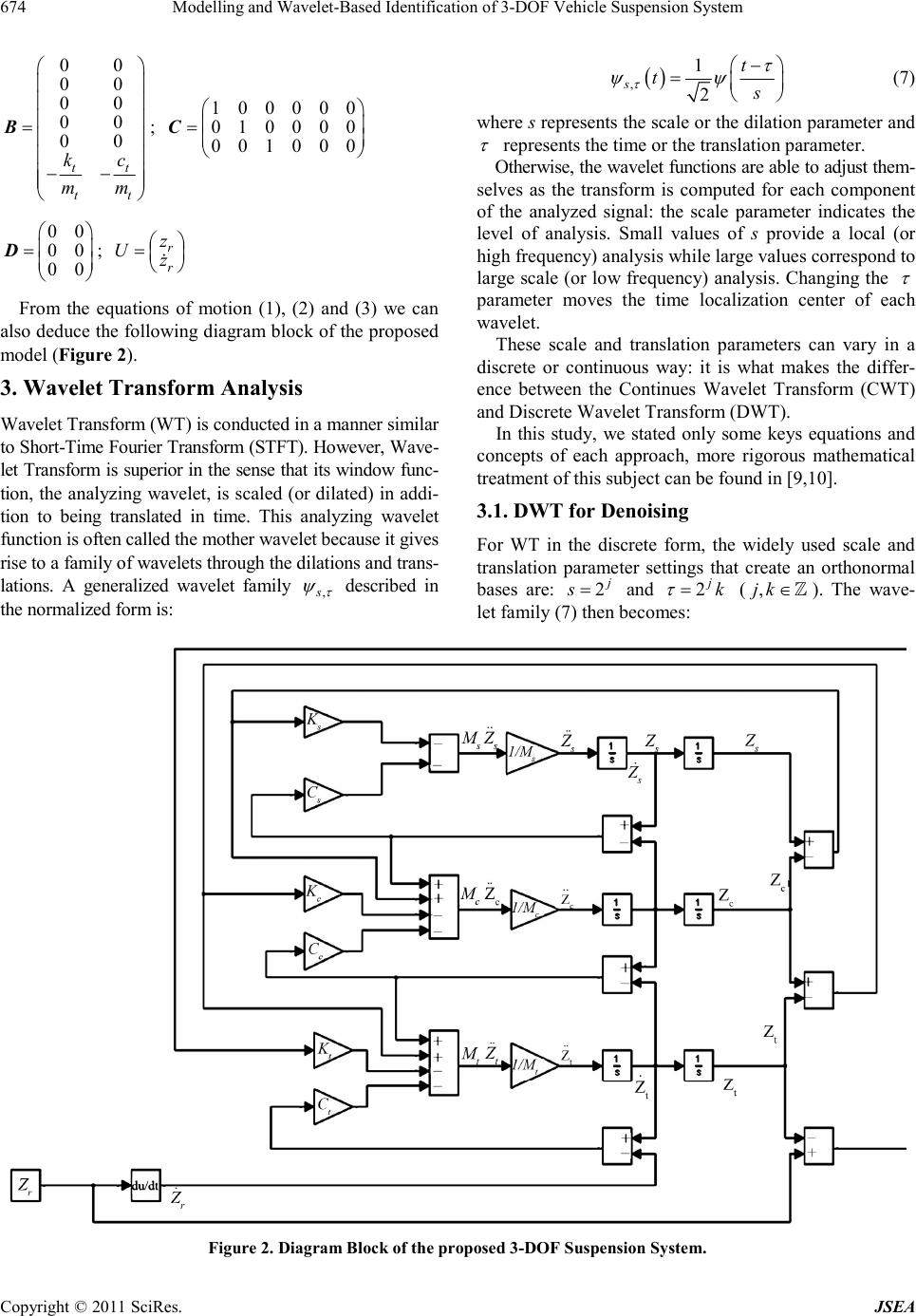 Modelling and Wavelet-Based Identification of 3-DOF Vehicle Suspension System Cop yright © 2011 Sci Res. JSEA 674 ,1 2 s t t 00 00 00 00 00 tt tt kc mm B; (7) 100000 010000 C001000 r r where s represents the scale or the dilation parameter and represents the time or the translation parameter. Other wise, t he wavelet functions are ab le to adj ust them- selves as the transform is computed for each component of the analyzed signal: the scale parameter indicates the level of analysis. Small values of s provide a local (or high frequency) analysis while large values correspond to large scale (or low frequency) analysis. Changing the parameter moves the time localization center of each wavelet. 00 00 00 D; , U From the equations of motion (1), (2) and (3) we can also deduce the following diagram block of the proposed model (Figure 2). These scale and translation parameters can vary in a discrete or continuous way: it is what makes the differ- ence between the Continues Wavelet Transform (CWT) and Discrete Wavelet Transform (DWT). 3. Wavelet Transform Analysis Wavelet Transform (WT) is conducted in a man ner similar to Short-Time Fourier Transform (STFT). However, Wave- let Transform is superior in the sense that its window func- tion, the analyzing wavelet, is scaled (or dilated) in addi- tion to being translated in time. This analyzing wavelet function is often called the mother wavelet because it gives rise to a family of wavelet s through the di lations and trans- lations. A generalized wavelet family In this study, we stated only some keys equations and concepts of each approach, more rigorous mathematical treatment of this subject can be found in [9,10]. 3.1. DWT for Denoising For WT in the discrete form, the widely used scale and translation parameter settings that create an orthonormal bases are: 2 s and 2 k (). The wave- let family (7) then becomes:,jk described in the normalized form is: Figure 2 . Diagram Block of the propose d 3-DOF Suspension System.  Modelling and Wavelet-Based Identification of 3-DOF Vehicle Suspension System675 2 ,22 j j jk x xk (8) Analogous to the FT , the DWT calculates wavelet co- efficients by taking the inner product of an input signal x with a function, that is in this case the wavelet fa- mily , k . DWT is designed to give good time resolu- tion and poor frequency resolution at high frequencies and good frequency resolution and poor time resolution at low frequencies. A signal is decomposed using the DWT into two sets of coefficients called approximations coefficients represent low-frequency signal components defined by Vetterli et al. [11]: 2 ,, ,2 2 jj jk jkd fxfx xk x (9) and details coefficients represent high-frequency signal components defined by: 2 ,, ,2 2 jj jk jkd fxfx xk x 1, (10) This decomposition, recursively repeated through fil- ter ing and d own-sampl ing ope rations us ing lo w-pass and high-pass filters (Figure 3), breaks the signal into lower level coefficient sets. Without manipulating these coeffi- cients, the original signal can be reconstructed exactly through the inverse DWT defined b y: ,21,2 kkmjmkmj m AhAgD m (11) where k and are respectively the high-pass and the low-pass filters (Figure 3). k h Manipulating wavelet coefficients prior to signal recon- struction changes the original signal. The original signal can be modified, enhanced or denoised through various coe- fficient manipulation operations. In our work, the DWT will be used to denoise the response of the system on the road to identify hi s mo d a l p a ram e te rs using th e CWT meth o d. Figure 3. Signal decomposition using DWT and reconstruc- tion using in verse DWT. 3.2. CWT for Modal Identification The Continuous Wavelet Transform (CWT) is defined as the convolution of the signal and the scaled-shifted versions ,ab xt of an analyzing function called the mother wavelet: * ,, , ,d ss s CWTxx ttx ttt (12) where *, is the complex conjugate of the analyzing function , . One of the most widely used mother wavelet for pa- rameter identification is the well-known modified Morlet wavelet defined by [12-14] : 2 0 jt tN tee (13) where 0 is the central pulsation of the Morlet mother wavelet and N is parameter introduced to control the shape of the basic wavelet intend to offer a better compromise in terms of localization, in both time and frequency for a signal. The optimal value of N is deter mined by minimization of the wavelet coefficients entropy [13] defined by: Shannon 1 log m j j WENWC WC (14) where 1 m ji i WC wcwc and is the set of wavelet coefficient energies. ;1,2 i wc im For a linear damped multi-DOF system with real modes, the free-decay response and impulse response can be used for modal identification. Hence, a simulated free- decay response with p modes is employed as the analyti- cal signal to investigate the CWT based time-frequency decompositions. Suppose the signal is given by: 2 00 11 ()cos 1 kk pp t kk kk kk xtxA et k (15) where 0k is the amplitude of th e kt h mode, 0k is the phase lag, k is the damping ratio and k is the natural pulsation. Since the wavelet transforms are linear repre- sentation of the signal, it follows that the CWT of this multi-co mponents si gnal is: 20 ,, , 11 1 *2 0, 1 () 1 2 kkk kk pp ssksk kk pj kskk k CWT xCWTxCWTx sAes e (16) Thus, the CWT works as a time-frequency filter and for a fixed value k of the scale parameter s, which maxi- Cop yright © 2011 Sci Res. JSEA  Modelling and Wavelet-Based Identification of 3-DOF Vehicle Suspension System 676 mizes * ,12 kk s , only the mode associated with k gives a significant contribution in the CWT, while all others are negligible: 20 , 1 *2 01 2 k kkk kk sk j k kkkk CWT x sAe se (17) These regions where the amplitude of the CWT is maximum are called the ridges. By extracting the values of the wavelet coefficients along the ridge yields the skeleton of the CWT. So, the CWT of each separated mode is defined by a skeleton expressed as follows: ,k k i skk CWT xAe (18) which implies that t he CWT is able to decompose a multi- component signal into separated modes and to represent them of a complex-valued signals each one defined by amplitude k A and a phase angle k . Note that the phase angle of this skeleton is: 20 1 kkkk ab (19) where a is the slope of this linear curve, and by ap- plying logarithmic operator to the amplitude of the ske- leto n, we obta i n: * 0 lnln 2 k kkk kkk AA s AA ab Consequently, the natural pulsation k and the damp- ing ratio k can be defined by combining the slopes of k and ln k A as follows: 22 k A k k aa a A (21) A specialized program has been developed on the MATLAB numeric computing environment for estimat- ing these parameters from the system response. This pro- gram includes the following procedures: Step 1: Calculate the wavelet entropy in order to deter- minate the optimal value of N corresponding to the opti- mal Morlet wavelet. Step 2: Transforming the time signal (response of the system) into time-scale domain using the CWT. Step 3: Detecting ridges and extracting corresponding skeletons. Step 4: Calculate modal parameters according to equa- tion (21) by least-square interp olation 4. Simulation s (20) In order to show the usefulness the WT in suspension stu- dy, the proposed 3-DOF suspension system was created using Simscape blockset library of Matlab software and the correspondent Simulink model shown on Figure 4 was implemented with the simple configuration given in Table 1. In the simulation study, the proposed model is exited Figure 4. Simulink model of the proposed 3-DOF suspension system. Cop yright © 2011 Sci Res. JSEA 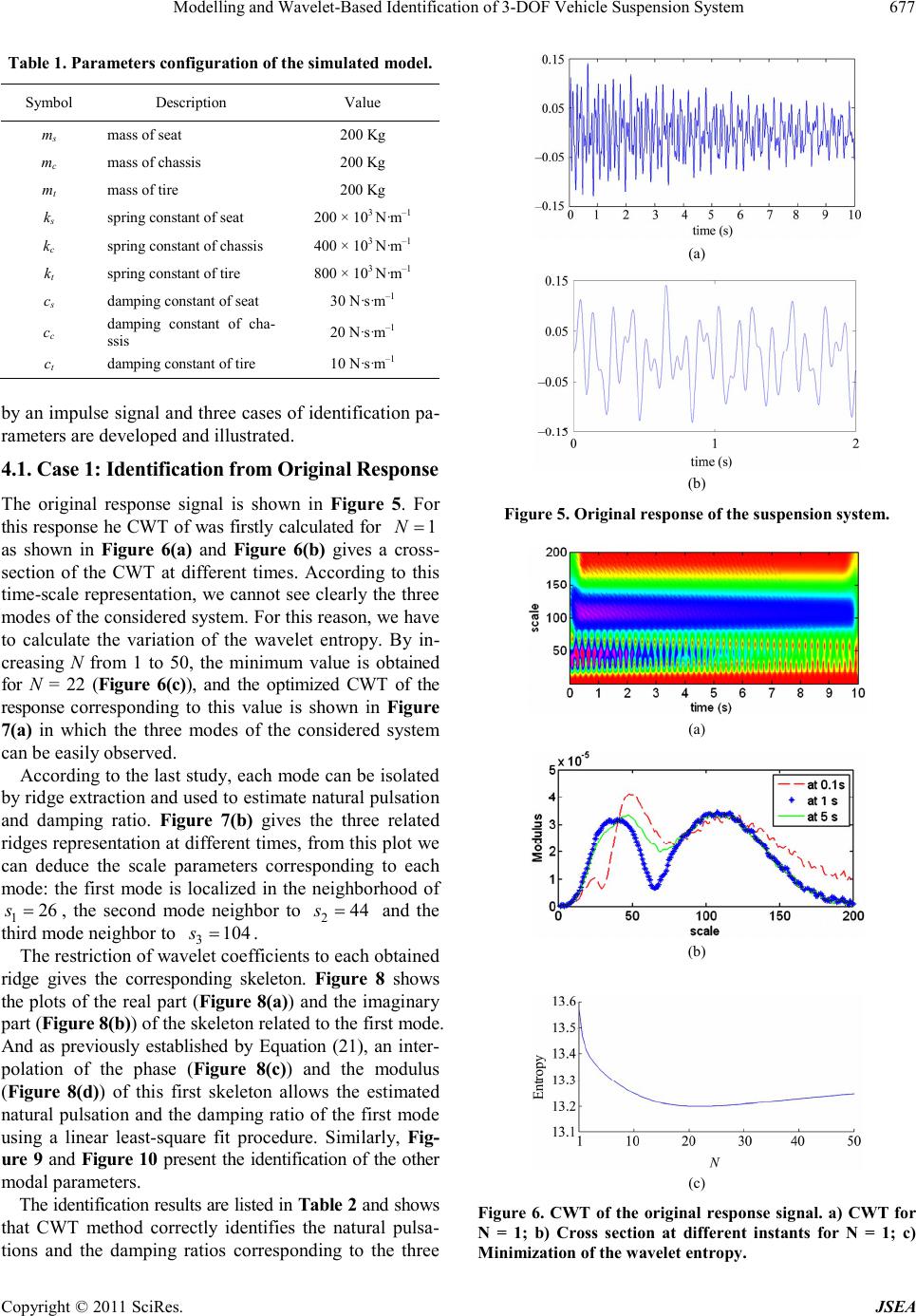 Modelling and Wavelet-Based Identification of 3-DOF Vehicle Suspension System677 Table 1. Parameter s conf iguration of the simulated model. Symbol Description Value ms mass of seat 200 Kg mc mass of chassis 200 Kg mt mass of tire 200 Kg ks spring constant of seat 200 × 103 N·m–1 kc spring constant of chassis 400 × 103 N·m–1 kt spring constant of tire 800 × 103 N·m–1 cs damping constant of seat 3 0 N·s·m–1 cc damping constant of cha- ssis 20 N·s·m–1 ct d amping constant of tire 10 N·s ·m–1 by an impulse signal and three cases of identification pa- rameters are developed and illustrated. 4.1. Case 1: Identification from Original Response The original response signal is shown in Figure 5. For this re sponse he CWT of was fir stly calc ulated fo r 1N as shown in Figure 6(a) and Figure 6(b) gives a cross- section of the CWT at different times. According to this time-scale representation, we cannot see clearly the three modes of the considered system. For this reason, we have to calculate the variation of the wavelet entropy. By in- creasing N from 1 to 50, the minimum value is obtained for N = 22 (Figure 6(c)), and the optimized CWT of the response corresponding to this value is shown in Figure 7(a) in which the three modes of the considered system can be easily observed. According to the last study, each mode can be isolated by ridge extraction and used to esti mate natural pulsation and damping ratio. Figure 7(b) gives the three related ridges representation at different times, from this plot we can deduce the scale parameters corresponding to each mode: the first mode is localized in the neighborhood of 1, the second mode neighbor to and the third mode neighbor to . 26s244s 3 The restriction of wavelet coefficients to each obtained ridge gives the corresponding skeleton. Figure 8 shows the plots of the real part (Figure 8(a)) and the imaginary part (Figu re 8(b)) of the skeleton related to the first mode. And as previously established by Equation (21), an inter- polation of the phase (Figure 8(c)) and the modulus (Figure 8(d)) of this first skeleton allows the estimated natural pulsation and the damping ratio of the first mode using a linear least-square fit procedure. Similarly, Fig- ure 9 and Figure 10 present the identification of the other modal parameters. 104s The ide ntificatio n results are listed i n Table 2 and shows that CWT method correctly identifies the natural pulsa- tions and the damping ratios corresponding to the three (a) (b) Figure 5. Original resp onse of the suspension system. (a) (b) (c) Figure 6. CWT of the original response signal. a) CWT for N = 1; b) Cross section at different instants for N = 1; c) Minimization of t he wavel e t entropy. Cop yright © 2011 Sci Res. JSEA  Modelling and Wavelet-Based Identification of 3-DOF Vehicle Suspension System 678 (a) (b) Figure 7. CWT of the original response signal. a) CWT for N = 22; b) Cross section at different instants. Figure 8. Identification of the skelet on correspo nding to the 1st mode. a) Real part; b) Imaginary part; c) Phase; d) Envelop. Figure 9. Identification of the skeleton corresponding to the 2nd mode. a) Real pa rt; b) Imaginar y part; c ) Phase; d ) Enve lop. Figure 10. Identification of the skeleton corresponding to the 3rd mode. a) Real part; b) Imaginary part; c) Phase; d) En- velop. modes. We note that the damping ratio is slightly less ac- curate than the natural pulsation because its value is es- timated from that previously estimated for the pulsation which causes a propagation of error. 4.2. Case 2: Identification from Noised Response In this case, two white Gaussian noises with Signal-to- Noise Ratio (SNR) equal to 20 dB and 2 dB were added to the original response in order to simulate CWT perfor- mances under noisy conditions. Signals with the two levels of noise are shown on Figure 11 and Figure 12. The same developed identification procedure is applied (Figure 13). By minimization of the wavelet entropy, the optimal value of N is the same as in the first case. The CWT has been applied successfully at the two noise levels. Figure 14 gives the identification of the first mode in the case of SNR equal to 2 dB. The results are not as good as in the case without noise, but they are ac- ceptable as shown in Table 2. 4.3. Ca se 3: I de nt ific at io n f ro m D en oi se d R es pon se In this case, the DWT-based denoising process was ap- plied to the previous two noised signals using Symlet wavelet and the troubles components affecting the signal were deleted as shown in Figure 15. Also in this case the identification was made following the same procedure. The results are similar to the previous and that is why only the identification of the first mode is represented in Figure 16. Table 2 presents a comparison between actual and es- timated parameters. In order to highlight the results ob- tained in each case, it useful to introduce a simple meas- ure of the error estimation for a given modal parameter estimated estimated via the CWT and compared to the exact value actual . Therefore, the Mean Absolute Error (MAE) which is an average of the absolute errors actual estimatedi deduced in a case with the three modal parameters of the system. This MAE is given by (22) and is introduced at the last column Table 2 . Cop yright © 2011 Sci Res. JSEA 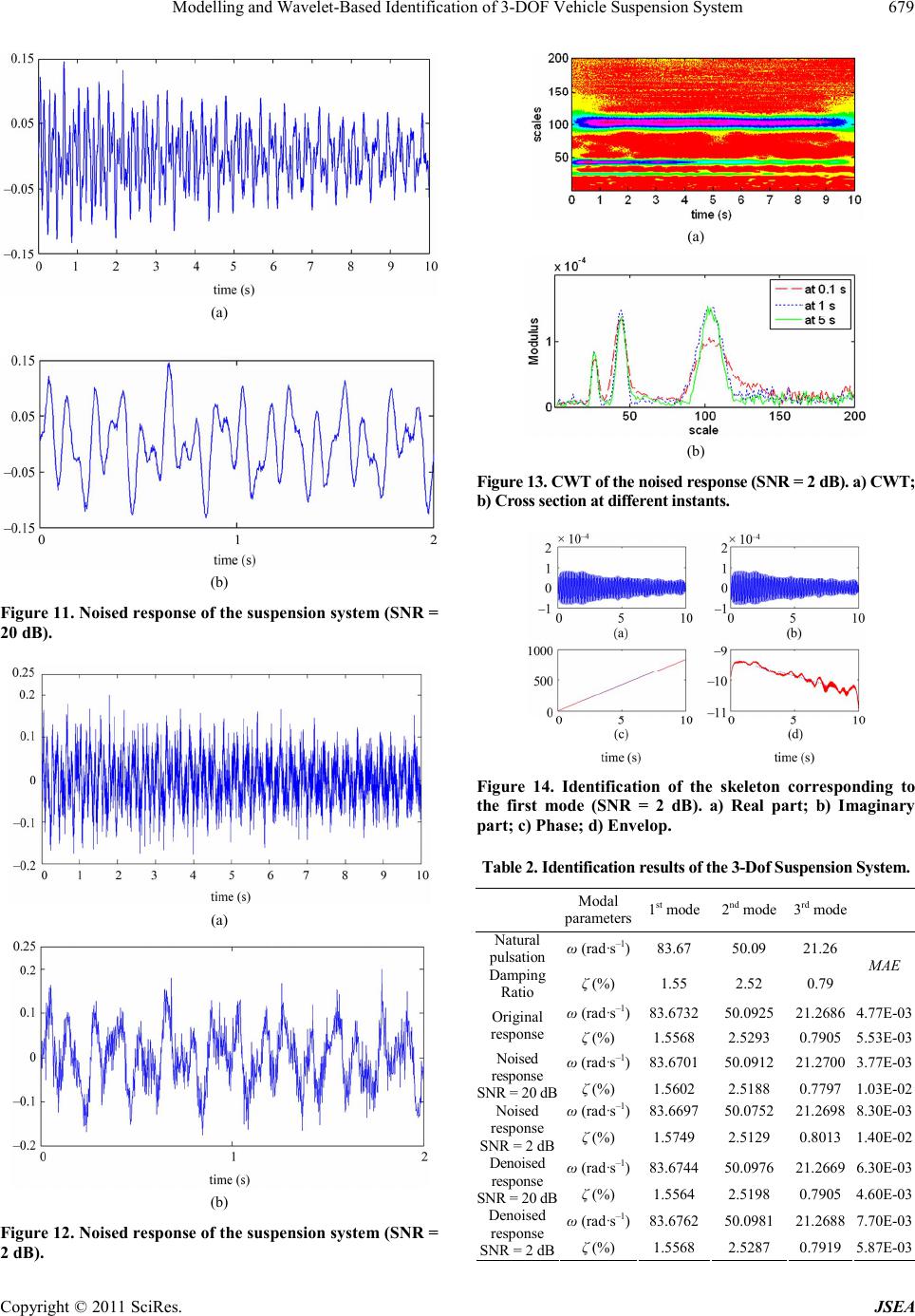 Modelling and Wavelet-Based Identification of 3-DOF Vehicle Suspension System679 (a) (b) Figure 11. Noised re spo nse of the sus pension system (SNR = 20 dB). (a) (b) Figure 12. Noised re spo nse of the sus pension system (SNR = 2 dB). (a) (b) Figure 13. CW T of the noised response (SNR = 2 dB). a) CWT ; b) Cr os s section at d if f eren t instan ts . Figure 14. Identification of the skeleton corresponding to the first mode (SNR = 2 dB). a) Real part; b) Imaginary part ; c) Phase; d) Envelop. Table 2. Identification results of the 3-Dof Suspension System. Modal parameters 1st mode 2nd mode 3rd mode Natural pulsation ω (rad·s–1)83.67 50.09 21.26 Damping Ratio ζ (%) 1.55 2.52 0.79 MAE ω (rad·s–1 )83.6732 50.0925 21.26864.77E-03 Original response ζ (%) 1.5568 2.5293 0.79055.53E-03 ω (rad·s–1 )83.6701 50.0912 21.27003.77E-03 Noised response SNR = 20 dBζ (%) 1.5602 2.5188 0.77971.03E-02 ω (rad·s–1 )83.6697 50.0752 21.26988.30E-03Noised response SNR = 2 dBζ (%) 1.5749 2.5129 0.80131.40E-02 ω (rad·s–1 )83.6744 50.0976 21.26696.30E-03 Denoised response SNR = 20 dBζ (%) 1.5564 2.5198 0.79054.60E-03 ω (rad·s–1 )83.6762 50.0981 21.26887.70E-03 Denoised response SNR = 2 dBζ (%) 1.5568 2.5287 0.79195.87E-03 Cop yright © 2011 Sci Res. JSEA  Modelling and Wavelet-Based Identification of 3-DOF Vehicle Suspension System 680 Figure 15. Denoising of the noisy response (SNR = 2) using DWT wi th Symlet w avelet. a) Nois y signal; b) Denoise d sig- nal; c) Dele ted noise. Figure 16. Identification of the skeleton corresponding to the first mode of the denoised response (SNR = 2 dB). a) Real part; b) I maginary part; c ) Phase; d) Envelop. 3 actual estimated 1 1 3 MAE (22) The simulation results obtained give a very accurate estimation of the actual parameters. This verifies the ef- fectiveness of the denoising and identification method based on DWT and CWT for the proposed model of sus- pension system. 5. Conclusions We have proposed in this paper a 3-DOF model of a quar- ter-vehicle suspension. After a dynamic study and the mo- deling of the system, we have investigated the perform- ances of the Wavelet analysis in the identification of pul- sation and da mping para meters of the s ystem. Due to its time-scale representation of signals, and the location of a mode by a ridge and the corresponding ske- leton, the CWT was able to identify the three modes of suspension syste m in all case s. In the case of poor resolution, the first two modes were not distinguishable, for this a compromise between fre- quency and temporal resolutions has been established by calculating the entropy of wavelet coefficients, and was able to optimize the CWT to better locate these particular modes. The important advantage of this approach is that it is not too sensitive to noise. Indeed, for all different noise levels, the modal identification was made with low error rates. The simulation results obtained underlined the ac- curacy and the efficiency of the developed method in the cases wher e the respo nse signal s are denoi sed by the DW T, and even in the presence of noise. Finally, we can conclude that wavelets are a powerful tool for the modal analysis in vibration applications es- pecially for suspension system s. REFERENCES [1] L. Zhu, Y. Zhu, M. Mao and M. Gu, “A New Method for Sparse Signal Denoising Based on Compressed Sensing, Second International Symposium on Knowledge Acquisi- tion and Modeling,” Second International Symposium on Knowledge Acquisition and Modeling, Wuhan, 30 Novem- ber-1 D e cember 2009, pp. 3 5-38. [2] D. Giaouris, J. W. Finch, O. C. Ferreira, R. M. Kennel and G. M. El-Murr, “Wavelet Denoising for Electric Dri- ves,” IEEE Transactions on Industrial Electronics, Vol. 5, No. 2, 2008, p p. 5 43-550. doi:10.1109/TIE.2007.911943 [3] H. S. Hu, J. Wang, S. X. Qian and X. Z. Jiang, “Test Modeling and Parameter Identification of a Gun Magnetor- heological Recoil Damper,” International Conference on Mechatronics and Automation, Changchun, 9-12 August 2009, pp. 3431-343 6. [4] N. Amann, J. Böcker and F. Prenner, “Active Damping of Drive Train Oscillations for an Electrically Driven Vehi- cle,” IEEE/ASME Transactions on Mechatronics, Vol. 9, No. 4, 2004, pp. 697-700. do i:10.1109/TMECH.2004.839036 [5] S.-L. Chen, J.-J. Liua and H.-C. Laia, “Wavelet Analysis for Identification of Damping Ratios and Natural Frequen- cies,” Journal of Sound and Vibration, Vol. 323, No. 1-2, 2009, pp . 130-147. doi:10.1016/j.jsv.2009.01.029 [6] J. Slavic, I. Simonovski and M. Boltezar, “Damping Iden- tification Using a Continuous Wavelet Transform: Applica- tion to Real Data,” Journal of Sound and Vibration, Vol. 262, No. 2, 20 03, pp. 2 91- 3 07. doi:10.1016/S0022-460X(02)01032-5 [7] D. S. Laila, A. R. Messina and B. C. Pal, “A Refined Hilbert-Huang Transform with Applications to Interarea Cop yright © 2011 Sci Res. JSEA  Modelling and Wavelet-Based Identification of 3-DOF Vehicle Suspension System Cop yright © 2011 Sci Res. JSEA 681 Oscillation Monitoring,” IEEE Transactions on Power Sys- tems, Vol. 24, 2009, pp. 610-620. doi:10.1109/TPWRS.2009.2016478 [8] M. Zheng, F. Shen, Y. Dou and X. Yan , “Modal Identifi- cation Based on Hilbert-Huang Transform of Structural Response with SVD Preprocessing,” Acta Mechanica Si- nica, Vol. 25, No. 6, 2009, pp. 883-888. [9] I. Daubenchies, “The Wavelet Transform, Time-Frequen- cy Locali sation and Signal Anal ysis,” IEEE Transactions on Information Theory, Vol. 36, No. 5, 1990, pp. 961-1005. doi:10.1109/18.57199 [10] O. Rioul and M. Vetterli, “Wavelets and Signal Process- ing,” IEEE Signal Processing Magazine, Vol. 8, No. 4, 1991, pp. 14- 3 8. doi:10.1109/79.91217 [11] M. Vetterli and C. Herley, “Wavelets and Filter Banks: The- ory and Design,” IEEE Transaction on Signal Processing, Vol. 40, No. 9, 1992, pp. 2207-2232. doi:10.1109/78.157221 [12] W. J. Staszewski, “Wavel et Based Compression and Fea- ture Selection for Vibration Analysis,” Journal of Sound and Vibration, Vol. 211, No. 5, 1998, pp. 735-760. doi:10.1006/jsvi.1997.1380 [13] J. Lardies and S. Gouttebroze, “Identification of Modal Parameters Using the Wavelet Transform,” International Journal of Mechanical Sciences, Vol. 44, No. 11, 2002, pp. 2263-2283. doi:10.1016/S0020-7403(02)00175-3 [14] J. Lardies, “Identification of a Dynamical Model for an Acoustic Enclosure Using the Wavelet Transform,” Ap- plied Acoustics, Vol. 68, No. 4, 2007, pp. 473-490. doi:10.1016/j.apacoust.2006.03.010
|