 Journal of High Energy Physics, Gravitation and Cosmology, 2019, 5, 140-148 http://www.scirp.org/journal/jhepgc ISSN Online: 2380-4335 ISSN Print: 2380-4327 10.4236/jhepgc.2019.51006 Dec. 20, 2018 140 Journal of High Energy Physics, G Generation Model of Particle Physics with Excited Rishon States Brian Albert Robson Department of Theoretical Physics, Research School of Physics and Engineering, The Australian National University, Canberra, Australia It is proposed that the Generation Model (GM) of particle physics, which de- scribes the elementary particles, the six leptons, the six quarks and the three weak bosons, of the Standard Model (SM) as composite particles in terms of three kinds of rishons and their antiparticles may be mimicking a simple model, employing only two kinds of rishons and their antiparticles. Keywords Generation Model, Rishon, Excited Rishon State 1. Introduction The Standard Model (SM) [1] of particle physics assumes that the six leptons: electron neutrino ( ), electron ( ), muon neutrino ( ), muon ( ), tau neutrino ( ), tau ( ) and the six quarks: up ( u ), down ( d ), charmed ( c ), strange ( s ), top ( t ) and bottom ( b ), which are the building blocks of matter, are elementary particles. This assumes that the leptons and quarks have no sub- structure, although there exists considerable indirect evidence to the contrary [2]. This indicates that the leptons and quarks possess no internal energy content to provide their mass, contrary to the 1905 conclusion of Einstein [3]: the mass of a body m is a measure of its energy content E and is given by , where c is the speed of light in a vacuum. Although in the SM, the mass of a hadron, e.g. a proton, arises essentially (≈99%) from the energy content of its constituent quarks and gluons, in agreement with Einstein’s conclusion, the masses of the elementary leptons and quarks are assumed [4] to arise in a completely different manner, involving the so-called Higgs mechanism [5] [6]. Thus the SM does not provide a unified Robson, B.A. 9) Generation Model of Particle Phys- ics with Excited Rishon States . Journal of High Energy Physics , Gravitation and Cos , , 140-148. //doi.org/10.4236/jhepgc.2019.51006 October 22, 2018 December 17, 2018 December 20, 2018 9 by author and Research Publishing Inc. work is licensed under the Creative Commons Attribution International 4.0). http://creativecommons.org/licenses/by/4.0/  B. A. Robson 10.4236/jhepgc.2019.51006 141 Journal of High Energy Physics, G origin of mass, contrary to Einstein’s conclusion. Furthermore, the SM does not provide any physical explanation, as distinct from the purely mathematical Higgs mechanism, for the origin of the masses of the leptons and quarks, as discussed by Lyre [7]. The Generation Model (GM) [2] [8] of particle physics, which was developed primarily to describe the three generations of leptons and quarks of the SM, [9] led to a composite model of all the elementary particles of the SM: the six leptons, the six quarks and the weak bosons, W and Z , mediating the weak interactions. The composite nature of these elementary particles of the SM, provided their constituents are massless , allows their masses to arise in agreement with Einstein’s conclusion so that the GM provides a unified description of the origin of all mass and hence has no need for the Higgs mechanism to generate the mass of any particle. The substructure of leptons and quarks in the GM is described in terms of three kinds of spin- massless elementary particles called “rishons”, T , V and U and their antiparticles, , and . The T -rishon carries electric charge , while both the V -rishon and U -rishon are electrically neutral. Both the T -rishon and the V -rishon were initially introduced by Harari [10] in a schematic composite model of leptons and quarks in 1979. Harari named these two elementary particles of his schematic composite model “rishons” after the Hebrew word for first or primary. Also independently in 1979, Shupe [11] introduced a very similar schematic composite model of leptons and quarks in which the spin- massless elementary particles were called “quips” (quark inner parts). Again the first generation of composite leptons and quarks were described in terms of only two quips: with charge and with charge . The and quips are equivalent to the T and V rishons of Harari, respectively. Shupe assumed that there was no mixing of quip and antiquip fields in forming lepton and quark composites and that both the quip particles and antiquip antiparticles existed in an s state. With these assumptions, the number of possible charge states is eight and these may be associated with the first generation of fermions and their antiparticles. Harari’s model essentially made the same assumptions. The GM [2] [8] is based upon a unified classification scheme of composite leptons and quarks that employs only three conserved additive quantum numbers: electric charge Q , particle number p and generation quantum number g . Table 1 gives these three additive quantum numbers allotted in the GM to the three kinds of rishons. For each rishon additive quantum number N , the corresponding antirishon has the additive quantum number - N . For each composite lepton or quark, the electric charge is related to the number of T -rishons and the number of -antirishons; the particle number 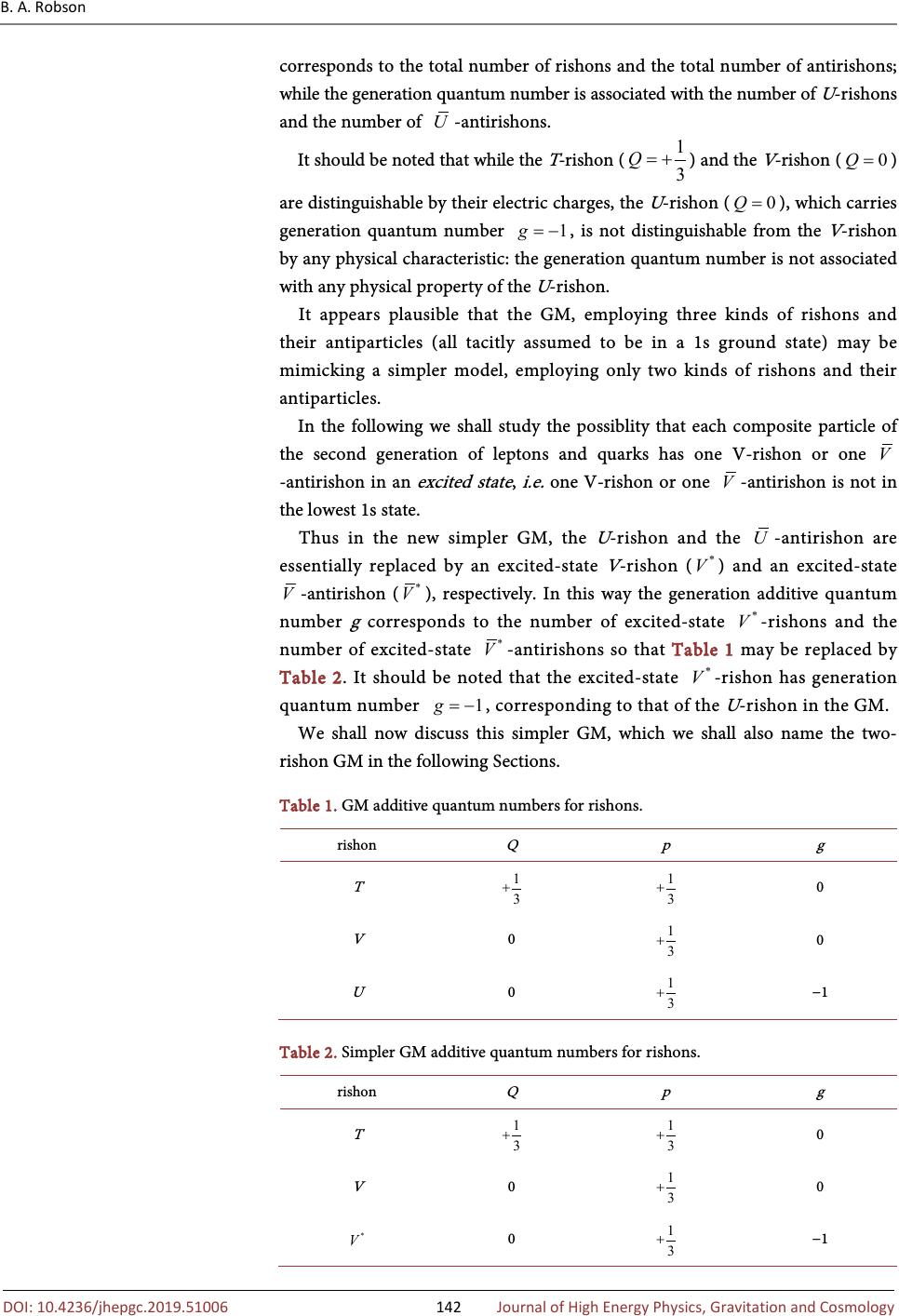 B. A. Robson 10.4236/jhepgc.2019.51006 142 Journal of High Energy Physics, G corresponds to the total number of rishons and the total number of antirishons; while the generation quantum number is associated with the number of U -rishons and the number of -antirishons. It should be noted that while the T -rishon ( ) and the V -rishon ( ) are distinguishable by their electric charges, the U -rishon ( ), which carries generation quantum number , is not distinguishable from the V -rishon by any physical characteristic: the generation quantum number is not associated with any physical property of the U -rishon. It appears plausible that the GM, employing three kinds of rishons and their antiparticles (all tacitly assumed to be in a 1s ground state) may be mimicking a simpler model, employing only two kinds of rishons and their antiparticles. In the following we shall study the possiblity that each composite particle of the second generation of leptons and quarks has one V-rishon or one -antirishon in an excited state , i.e. one V-rishon or one -antirishon is not in the lowest 1s state. Thus in the new simpler GM, the U -rishon and the -antirishon are essentially replaced by an excited-state V -rishon ( ) and an excited-state -antirishon ( ), respectively. In this way the generation additive quantum number g corresponds to the number of excited-state -rishons and the number of excited-state -antirishons so that Table 1 may be replaced by Table 2. It should be noted that the excited-state -rishon has generation quantum number , corresponding to that of the U -rishon in the GM. We shall now discuss this simpler GM, which we shall also name the two- rishon GM in the following Sections. Table 1. GM additive quantum numbers for rishons. T 0 V 0 0 U 0 −1 Table 2. Simpler GM additive quantum numbers for rishons. T 0 V 0 0 0 −1  B. A. Robson 10.4236/jhepgc.2019.51006 143 Journal of High Energy Physics, G 2. The Two-Rishon Generation Model In the GM [2] [8] it is assumed that each of the three kinds of rishons, T , V and U , carries a color charge, red, green or blue, while each of their antiparticles, , and , carries an anticolor charge, antired, antigreen or antiblue. The GM also assumes that the interaction responsible for binding rishons and antirishons together to form colorless leptons and colored quarks is analogous to the strong color interaction, Quantum Chromo-Dynamics (QCD), that binds quarks and antiquarks together to form colorless baryons and mesons in the SM. [1] In the GM the color interaction is mediated by massless hypergluons, corresponding to a local gauged color symmetry, that are analogous to the massless gluons, which mediate the QCD color interaction of the SM. In the two-rishon GM, the rishon structures of the leptons and quarks comprising the first generation (see Table 3) remain unchanged, since the first generation particles and antiparticles do not contain a U -rishon or a -antirishon. It should be noted that contrary to the 1979 Harari-Shupe model, [10] [11] the GM replaces the V -rishon by its antiparticle -antirishon and vice-versa, in order that the u -quark has particle number , corresponding to its baryon number in the SM. In the simpler GM the U -rishon and the -antirishon of the GM are replaced by an excited-state V -rishon ( ) and an excited-state -antirishon ( ), respectively. Thus the color structures of the second generation of leptons and quarks involving -rishons or -antirishons remain unchanged from those of the GM, since the -rishon and the -antirishon are assumed to carry the same color charges as the U -rishon and the -antirishon, respectively. In the GM the rishon structures of the second generation of leptons and Table 3. Two-rishon GM of first generation of leptons and quarks. +1 +1 0 u 0 0 0 −1 0 0 +1 0 d 0 0 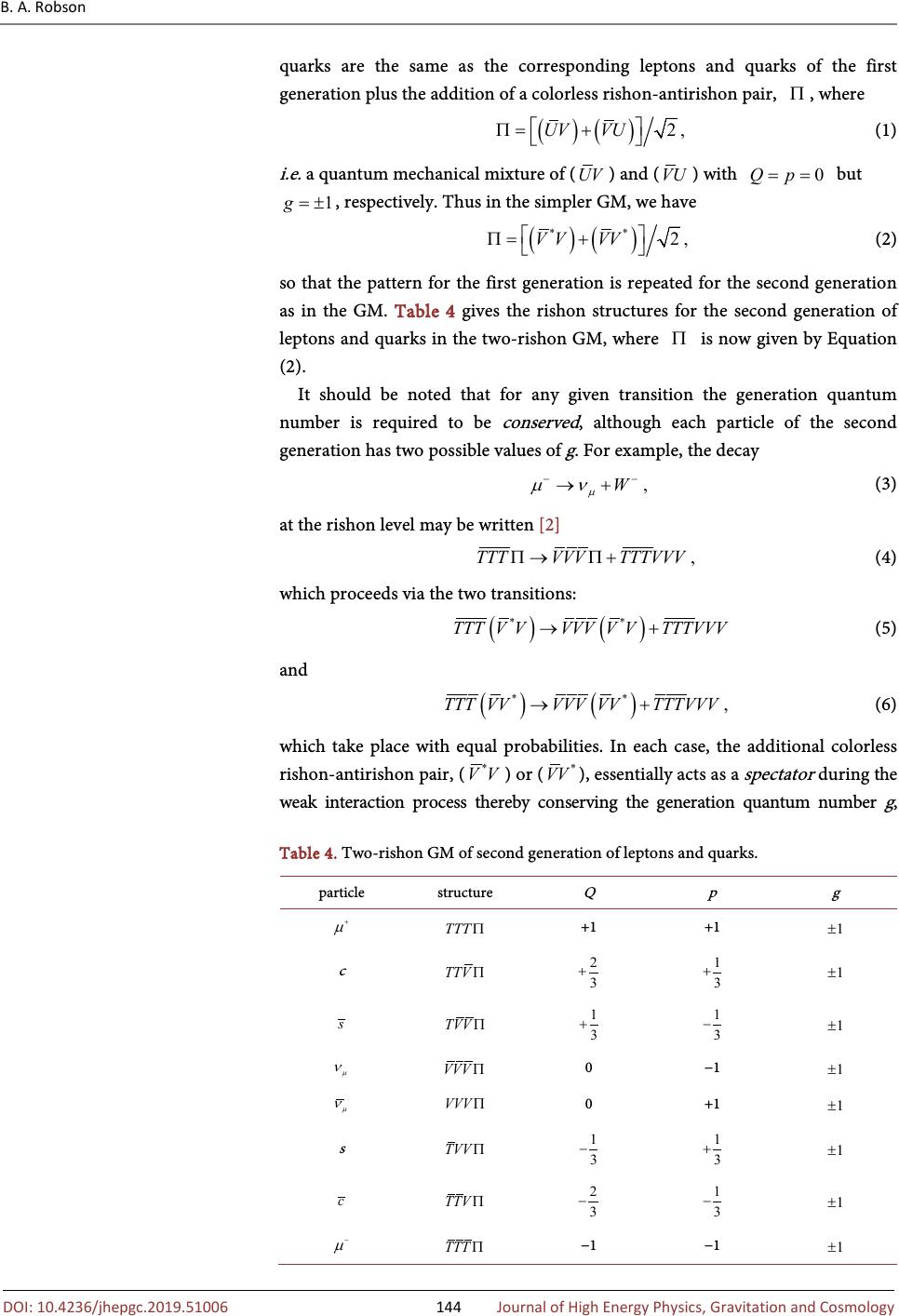 B. A. Robson 10.4236/jhepgc.2019.51006 144 Journal of High Energy Physics, G quarks are the same as the corresponding leptons and quarks of the first generation plus the addition of a colorless rishon-antirishon pair, , where (1) i.e. a quantum mechanical mixture of ( ) and ( ) with but , respectively. Thus in the simpler GM, we have (2) so that the pattern for the first generation is repeated for the second generation as in the GM. Table 4 gives the rishon structures for the second generation of leptons and quarks in the two-rishon GM, where is now given by Equation (2). It should be noted that for any given transition the generation quantum number is required to be conserved , although each particle of the second generation has two possible values of g . For example, the decay (3) at the rishon level may be written [2] (4) which proceeds via the two transitions: (5) and ()() ** ,TTTVVVVVVVTTTVVV→+ (6) which take place with equal probabilities. In each case, the additional colorless rishon-antirishon pair, ( ) or ( ), essentially acts as a spectator during the weak interaction process thereby conserving the generation quantum number g , Table 4. Two-rishon GM of second generation of leptons and quarks. +1 +1 c 0 −1 0 +1 s −1 −1  B. A. Robson 10.4236/jhepgc.2019.51006 145 Journal of High Energy Physics, G which has the value +1 and −1, respectively. In the GM the rishon structures of the third generation of leptons and quarks are the same as the corresponding leptons and quarks of the first generation plus the addition of two rishon-antirishon pairs, , that are given by Equation (1). Thus in the simpler GM, the rishon-antirishon pairs, , are described by Equation (2). In this way the pattern of the first and second generation is also continued for the third generation. Table 5 shows the rishon structures for the third generation of leptons and quarks in the two-rishon GM. In the GM the rishon structure of the particle is for example: () ()() ()() () ()() 2TTTTTTUVUVUVVUVUUVVUVU ΠΠ=+++ (7) and each particle of the third generation is a similar quantum mechanical mixture of components. In each case, the additional colorless rishon-anti- rishon pairs, ( ) and/or ( ), essentially act as spectators during any weak interaction process. Again it should be noted that for any given transition the generation quantum number is required to be conserved, although each particle of the third generation now has three possible values of g . Thus in the simpler GM for example, the decay (8) at the rishon level may be written (9) which proceeds via the four transitions: ()() () () **** ,TTTVVVVVVVVVVVTTTVVV →+ (10) () () () () **** ,TTTVVVVVVVVVVVTTT VVV→+ (11) () ( ) () () **** , TTTVVVVVVVVVVVTT TVVV→+ (12) Table 5. Two-rishon GM of third generation of leptons and quarks t 0 −1 0 +1 b −1 −1  B. A. Robson 10.4236/jhepgc.2019.51006 146 Journal of High Energy Physics, G ()()()() **** ,TTTVVVVVVVVVVVTTTVVV→+ (13) which take place with equal probabilities. In each case, the additional two colorless rishon-antirishon pairs, , , or act as spectators during the weak interaction process, thereby conserving the generation quantum number g , which has the value +2, 0, 0 and −2, respectively. To summarize: the replacement of the U -rishon and its antiparticle -antirishon of the GM by an excited-state V -rishon ( ) and an excited-state -antirishon ( ), respectively, in the simpler GM, leads to an equivalent model of the three generations of composite leptons and quarks. 3. Excited Rishon States Since to date there is no direct evidence for any substructure of leptons or quarks, it is expected that the rishons and/or antirishons of each lepton or quark are localized within a very small volume of space by the strong QCD color interactions, acting between the colored rishons and/or antirishons. In QCD theory, the short-distance behavior of the color interactions in the GM is dominated by one-hypergluon exchange and is described by a Coulomb-like potential, analogous to that in atomic systems [12]. Thus it is expected that the lowest energy or ground rishon state is a 1s state. This was assumed in the current GM for each of the T , V and U rishons and their antiparticles, , and antirishons. Indeed the essential reason for introducing the U -rishon and its antiparticle -antirishon into the GM was to avoid annihilation processes, if the second and third generations of leptons and quarks involved colorless rishon-antirishon pairs . In the simpler GM, with the rishon-antirishon pair given by Equation (2), such annihilation processes are avoided, since the excited-state V -rishon ( ) and its antiparticle ( ) will be in an orthogonal quantum state, i.e. a 2s state. For the second and third generations of leptons and quarks, it is expected by analogy with atomic physics that the -rishon and its antiparticle ( ) will occupy a 2s state [13] [14]. 4. Conclusions and Discussion It has been demonstrated that the GM of particle physics, which describes the elementary particles of the SM of particle physics as composite particles in terms of three kinds of rishons and their antiparticles, may be replaced by a simpler equivalent model employing only two kinds of rishons and their antiparticles. In this simpler model that we have called the Two-Rishon Generation Model, the U -rishon of the GM has been replaced by an excited-state -rishon in a 2s state. If the -rishon occupies a 2s state in the composite systems describing the leptons and quarks of both the second and third generations, all the interactions  B. A. Robson 10.4236/jhepgc.2019.51006 147 Journal of High Energy Physics, G involving the leptons and quarks within the framework of the simpler GM are identical to those of the GM. In addition the simpler GM retains a unified origin of mass, the same kind of mass hierarchy of leptons and quarks and the same origin of gravity as the GM [2]. In particular, since the -rishon has the same parity as the U -rishon in the GM, the simpler GM also describes the origin of “apparent” CP violation in the system [2] [15]. The two-rishon GM contains fewer elementary particles (21 counting both particles and antiparticles and their three different color forms plus the mediating particles of the electromagnetic and the strong interactions) compared with the GM involving three kinds of rishons (27 elementary particles), which was a considerable improvement on the SM (61 elementary particles) [2]. In addition, the two-rishon GM provides a satisfactory understanding of the second and third generations of composite leptons and quarks that was not achieved in the 1981 dynamical model of Harari and Seiberg [16]. Conflicts of Interest The author declares no conflicts of interest regarding the publication of this pa- per. References [1] Gottfried, K. and Weisskopf, V.F. (1984) Concepts of Particle Physics. Vol. 1, Ox- ford University Press, New York. [2] Robson, B.A. (2012) The Generation Model of Particle Physics. In: Kennedy, E., Ed., Particle Physics , InTech, Rijeka, 1-28. https://doi.org/10.5772/35071 [3] Einstein, A. (1905) Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig. Annalen der Physik , 18, 639-641. https://doi.org/10.1002/andp.19053231314 [4] Aitchison, I.J.R. and Hey, A.J.G. (1982) Gauge Theories in Particle Physics. Hilger, Bristol. [5] Englert, F. and Brout, R. (1964) Broken Symmetry and the Mass of Gauge Vector Bosons. Physical Review Letters , 13, 321-323. https://doi.org/10.1103/PhysRevLett.13.321 [6] Higgs, P.W. (1964) Broken Symmetries and the Masses of Gauge Bosons. Physical Review Letters , 13, 508-509. https://doi.org/10.1103/PhysRevLett.13.508 [7] Lyre, H. (2008) Does the Higgs Mechanism Exist? International Studies in the Phi- losophy of Science , 22, 119-133. https://doi.org/10.1080/02698590802496664 [8] Robson, B.A. (2013) Progressing beyond the Standard Model. Advances in High Energy Physics , 2013, 341738. https://doi.org/10.1155/2013/341738 [9] Veltman, M. (2003) Facts and Mysteries in Elementary Particle Physics. World Scientific, Singapore. https://doi.org/10.1142/5088 [10] Harari, H. (1979) A Schematic Model of Quarks and Leptons. Physical Review Let- ters B , 86, 83-86. https://doi.org/10.1016/0370-2693(79)90626-9 [11] Shupe, M.A. (1979) A Composite Model of Leptons and Quarks. Physical Review Letters B , 86, 87-92. https://doi.org/10.1016/0370-2693(79)90627-0 [12] Griffiths, D.J. (1987) An Introduction to Elementary Particles. Wiley, NewYork. https://doi.org/10.1002/9783527618460  B. A. Robson 10.4236/jhepgc.2019.51006 148 Journal of High Energy Physics, G [13] Born, M. (1937) Atomic Physics. Blackie and Son Ltd., London. [14] Kawanai, T. and Sasaki, S. (2015) Potential Description of Charmonium and Charmed-Strange Mesons from Lattice QCD. Physical Review D , 92, 094503. https://doi.org/10.1103/PhysRevD.92.094503 [15] Morrison, A.D. and Robson, B.A. (2009) Decay of the Meson without CP Violation. International Journal of Modern Physics E , 18, 1825-1830. https://doi.org/10.1142/S0218301309013889 [16] Harari, H. and Seiberg, N. (1981) A Dynamical Theory for the Rishon Model. Phys- ics Letters B , 98, 269-273. https://doi.org/10.1016/0370-2693(81)90012-5
|