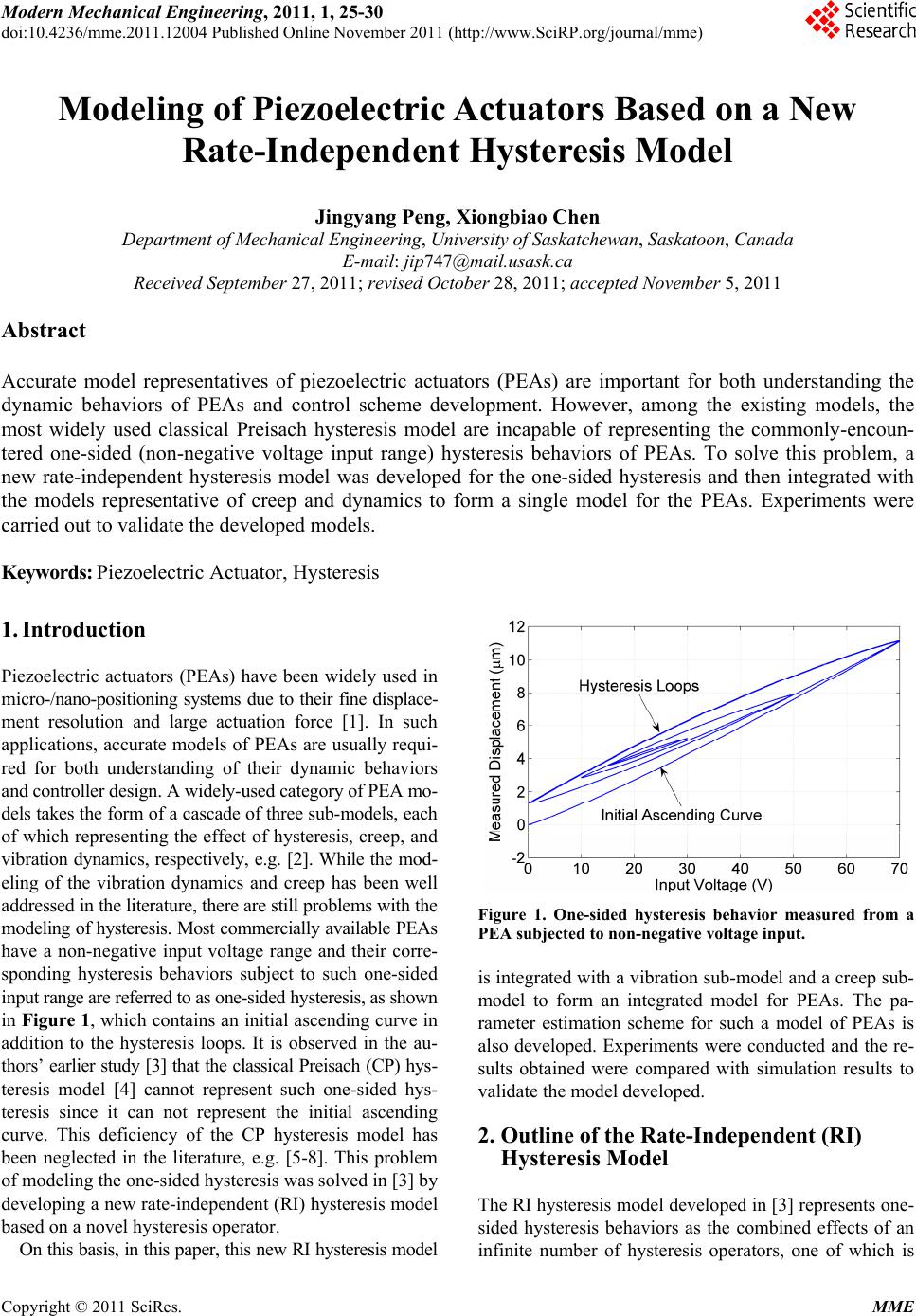
 Modern Mechanical Engineering, 2011, 1, 25-30 doi:10.4236/mme.2011.12004 Published Online November 2011 (http://www.SciRP.org/journal/mme) Copyright © 2011 SciRes. MME Modeling of Piezoelectric Actuators Based on a New Rate-Independent Hysteresis Model Jingyang Peng, Xiongbiao Chen Department of Mechanical Engineering, University of Saskatchewan, Saskatoon, Canada E-mail: jip747@mail.usask.ca Received September 27, 2011; revised October 28, 2011; accepted November 5, 2011 Abstract Accurate model representatives of piezoelectric actuators (PEAs) are important for both understanding the dynamic behaviors of PEAs and control scheme development. However, among the existing models, the most widely used classical Preisach hysteresis model are incapable of representing the commonly-encoun- tered one-sided (non-negative voltage input range) hysteresis behaviors of PEAs. To solve this problem, a new rate-independent hysteresis model was developed for the one-sided hysteresis and then integrated with the models representative of creep and dynamics to form a single model for the PEAs. Experiments were carried out to validate the developed models. Keywords: Piezoelectric Actuator, Hysteresis 1. Introduction Piezoelectric actuators (PEAs) have been widely used in micro-/nano-positioning systems due to their fine displace- ment resolution and large actuation force [1]. In such applications, accurate models of PEAs are usually requi- red for both understanding of their dynamic behaviors and controller design. A widely-used category of PEA mo- dels takes the form of a cascade of three sub-models, each of which representing the effect of hysteresis, creep, and vibration dynamics, respectively, e.g. [2]. While the mod- eling of the vibration dynamics and creep has been well addressed in the literature, there are still problems with the modeling of hysteresis. Most commercially available PEAs have a non-negative input voltage range and their corre- sponding hysteresis behaviors subject to such one-sided input range are referred to as one-sided hysteresis, as shown in Figure 1, which contains an initial ascending curve in addition to the hysteresis loops. It is observed in the au- thors’ earlier study [3] that the classical Preisach (CP) hys- teresis model [4] cannot represent such one-sided hys- teresis since it can not represent the initial ascending curve. This deficiency of the CP hysteresis model has been neglected in the literature, e.g. [5-8]. This problem of modeling the one-sided hysteresis was solved in [3] by developing a new rate-independent (RI) hysteresis model based on a novel hysteresis operator. On this basis, in this paper, this new RI hysteresis model Figure 1. One-sided hysteresis behavior measured from a PEA subjected to non-negative voltage input. is integrated with a vibration sub-model and a creep sub- model to form an integrated model for PEAs. The pa- rameter estimation scheme for such a model of PEAs is also developed. Experiments were conducted and the re- sults obtained were compared with simulation results to validate the model developed. 2. Outline of the Rate-Independent (RI) Hysteresis Model The RI hysteresis model developed in [3] represents one- sided hysteresis behaviors as the combined effects of an infinite number of hysteresis operators, one of which is  J. Y. PENG ET AL. 26 shown in Figure 2. Compared to the Preisach hysteresis operator, the hysteresis operator in Figure 2 has one more lower saturation value to account for the initial ascending curve in one-sided hysteresis. The two switching values satisfy . The hysteresis is then expressed mathe- matically as maxmin 0 ,, dd uu ft ut (1) where t is the hysteresis, i.e. the model output, and min u are the maximum and minimum input in history, respectively [3]. max u ut The double integration suggests that the hysteresis model output is the combined effect of an infinite number of hysteresis operators with bounded values of and , which can be explained via the geometric interpretation shown in Figure 3. Each hysteresis operator ut ,, is assigned to a point , on the α-β plane. All such , points are in a region satisfying max u T , min which is referred to as the limiting triangle 0. According to the values of 0u ,,ut S S , 0 is divided into three regions denoted by 0, 1, and 2, where T S 0 , 1 , and 2 , respectively. The interface between and the other two regions is a horizontal 0 S line characterized by 1max max 0utMM in which max is the maximum local maximum. The in- terface between and is a staircase line with vertex M 1 S2 S coordinates , where , ij mM 0,1, ,im and 1, 2,,jn , Figure 2. The novel hysteresis operator ,, ut [3]. Figure 3. Geometric interpretation of the RI hysteresis mo- del. and are the historical local ma- xima and min- ima of i m ut , respectively. The link in the 1-2 inter- face that attaches to the line S S is referred to as the - final link and it represents the influence of the changes in input ut to the shapes of , , and . This link 0 S S1 2 S is horizontal and goes up at a speed of ut when 0ut , and is vertical and goes left at a speed of ut when 0ut 0d . Noting that 0 Sut d 0 , so Equation (1) can be reduced to 12 12 ,dd ,dd SS ft (2) The motion of the final link will wipe out certain ver- texes and links, or , ij mM pairs whenever m ut m or n ut M. A modified version of the wipe-out prop- erty [4] of the CP hysteresis model governs such wipe-out processes. The modification is that in the RI hysteresis model, the first local minimum 0 and the maximum local maximummax are never wiped out. Besides, the congruency property [4] of the CP hysteresis model still applies to the hysteresis loops but not to the initial ascending curve in the RI hysteresis model as the initial ascending curve is not part of any hysteresis loops. 0m M Equations (1) and (2) involve double integration which is difficult to implement in practice, so an alternative model expression without calculus is desirable and is given in [3]. The rationale behind this alternative model expression is that the 1 and 2 regions in Equation (2) can be treated as a result of the unification and sub- S S traction of a series of triangular regions 11 , ii Sut ut and 2 , ii Sut ut 1 . Then the integration of ,,ut over each of such triangular regions can be pre-identified and used to calculate t through a series of adding and subtracting operations. Specifically, each of such triangular regions represents the shape change in 1 or 2as the input changes mo- notonically between two adjacent extrema S S i ut and 1i ut in the input history which are not wiped-out. The changes in the model output due to 11 Su t , ii t u and 2 are represented by the follow- ing two functions. 1 , i Sut ut i 11 11 1 , ,, ii ii Sut ut Fut utdd (3) 11 21 1 , ,, ii ii Sut ut Fut utdd (4) Thus, the RI hysteresis model output can be expressed as a linear combination of 11 , ii Fut ut and 2 , ii Fut ut 1 , as follows. Denoting two adjacent local minimum and local maximum by m and M, respectively, Copyright © 2011 SciRes. MME  J. Y. PENG ET AL. 27 1 the following relationships related to Equations (3) and (4) are obtain by using the congruency property and the property of the initial ascending curve. 1 11 11 , ,, ,dd Mm SMm FMm FmM f (5a) 2 22 , 2222 ,,dd 0 SMm m MMmMm FMm fff (5b) 2 2, initial ascending curve not traversed 0 initial ascending curve traversed FMm ,FmM (5c) where M () represents the part in 1, 2j t con- tributed by the S region at the moment when ut is initially increased form 0 to M; and Mm (1, 2fj ) the part in t contributed by the S M region at the mo- ment when is subsequent decreased to m from M. Assume that the historical local minima and maxima of that are not wiped out are mi ut 1 mm ut n 01nn mmax M0 0 00 mm mM M dur- ing , and 111 maxnn ut mi n during . Then, if the input monotonically increases, i.e., , one has 0 0 1n ut ut 11 111 0 1 122 1 22 ,, ,, ,, kk kk k n nkkk k nn n ftFM mFM m FutmF M mF Mm FMm Futm 1 , k (6) and if the input monotonically decreases, i.e., 0ut 2 11 111 0 111 1 2212 1 ,, ,, ,, n kk kk k nn n n kkk kn k ftFM mFM m FM mFMut , MmFMmFMut (7) For the ease of parameter identification, define two new functions as max1max ,0FMFM , (8) 12 ,,GMmF MmFMm (9) where is the model output increment when is increased from 0 to max along the initial as- cending curve, and is the model output dec- rement when is subsequently decreased to m. The values of max FM ut ut M ,GMm max FM M and under different m, M, and max are readily measurable from a hysterical plant, so suitable expressions of and ,GMm FM max ,GMm 0 k m can be found. This is to be described in Section 4. Finally, Substituting Equations (8) and (9) into Equa- tions (6) and (7) yields the alternative expression of the RI hysteresis model for practical uses. For ut 1 1 1 ,, n k k nn ft M m max FM GM ,, kk GMm Gut m n G (10) and for 0ut 1 1 1 ,, n k k ft M t max , n FM GM u kk GMm G k m (11) 3. A Model of Piezoelectric Actuators The model of PEA is developed by cascading a vibration sub-model and a creep sub-model to the above RI hys- teresis model, as shown in Figure 4. ut represents the voltage input, and t represents the displacement of the PEA or the model output. The vibration sub-model is represented by means of a second order system under the assumption that the mass driven by the PEA is much larger than the mass of the PEA itself [9], i.e., 2 11nn 2 txt ft (12) where and n are the damping ratio and the na- tural frequency, respectively; and t is the hysteresis being represented by using the RI hysteresis model dis- cussed in the previous section. Since the RI hysteresis t does not introduce phase lag, the phase lag between t and ut is resulted from the vibration sub-model (Given the fact that the magnitude of creep is very small, its phase lag can be neglected). Thus, the values of and n can be estimated by fitting the frequency-phase response of Equation (12) to the measured frequency- phase response of a PEA. The parameter identification of the RI hysteresis model involves the identification of the functions max FM and ,mGM. To do this, some input-output data or the values of t corresponding to certain inputs ut need to be found. However t is difficult to measure in practice, so in this study such f (t) values is calculated Figure 4. Integrated model of a PEA. Copyright © 2011 SciRes. MME  J. Y. PENG ET AL. 28 from Equation (12) by using 1 t and its derivatives when the PEA is subject to ut . It should be noted that in this process, creep is again neglected due to its small magnitude and t is taken as 1 t, which is meas- urable. The derivatives of 1 t can be approximately found either by firstly passing through the measured t through a low pass filter to suppress the noise and then differentiating the low pass filter output or by a state estimator such as an α-β-γ filter. Once such ut and f (t) data are obtained, a suitable expressions of max FM and can then be found with their parameters estimated (to be discussed in Section 4). ,GMm The creep in Figure 4 is represented by means of a linear dynamic system model taking 2 Gs 1 t as input and generating a creep displacement 2 t. 2 t is then added to 1 t to obtain the total displacement output of the PEA, t, as shown in Figure 5. The form and the parameters of s 2 can be determined by system identification methods. G Eventually, with a voltage input , a displacement output ut t in Figure 4 can be derived from Equations (10), (11), (12), and 1121 2 1 c GsXsXsXsX sXs Gs (13) where 1 s, 2 s, and s are the Laplace trans- forms of 1 t, 2 t, and t respectively. 4. Experiments and Results 4.1. Experiment Setup Experimental validations of the PEA model are carried out on a PEA (P-753, Physik Instrumente). The actuator can generate motion in a range of 15 μm with a resolu- tion of 0.5 nm. For displacement measurements, a built- in capacitive displacement sensor of the P-753 PEA with a resolution of 1nm was used. Both the actuator and the sensor are interfaced to a host computer via an I/O board (PCI-DAS1602/16, Measurement Computing Corporation) and controlled by SIMULINK programs. All measured displacements presented in this study were measured with a sampling interval of 0.05 ms. 4.2. Vibration Sub-Model Parameter Estimation As mentioned in the previous section, and n in Equation (12) were estimated by fitting the phase fre- quency response of Equation (12) to the measured re- sponse of the PEA based on the method of least squares. The phase frequency response curve of the PEA displa- cements was measured by feeding sinusoidal voltages between 0 and 1000 Hz to the PEA and then calculating the phase differences between the input voltages and the measured output displacements. The fitted results are shown in Figure 6, from which and n were esti- mated as 0.788 and 5352 rad/s, respectively. 4.3. RI Hysteresis Sub-Model Parameter Estimation To identify max FM and ,GM in Equations (8) and (9), the displacements of the PEA were measured under the voltage inputs determined by m 22 sin2001.5 pp pp ut VVt (14) where p is the peak-to-peak magnitudes. Since the frequency of voltage input, i.e., 100 Hz, was high, creep was insignificant over a few periods of the waveforms and thus neglected. The minimum and maximum of the voltage applied to the PEA were set to 0 V and 70 V, respectively. V p (or max ), M and m were then taken values from 0 V to 70 V with a step of 5 V, respectively and thus the series of VM ut were determined. By apply- ing ut of different p Vor max to the PEA, the dis- placements of the actuator were measured. Each meas- ured displacement waveform was the M 1 t in Equation (12) corresponding to a given . 1 ut t and 1 t 2 10 were estimated by an α-β-γ filter (8.7 , 3 3.9 10 , 3 102.4 ) from the measured 1 t. 1 t, 1 t, and 1 t were then substituted into Equa- tion (12) to calculate the “measured” t correspond- ing to the given ut . In the following, the values of t and the corresponding from the initial con- ditions of t ut 0 , 0ut , and were exam- ined. Once ft0 ut was increased to reach a given max from M 00ut , the corresponding t value was found and taken as a value of . Similarly, once ma FM x Figure 5. The creep sub-model, i.e., Gc(s) in Figure 4. Figure 6. Measured and estimated phase frequency responses. Copyright © 2011 SciRes. MME  29 J. Y. PENG ET AL. the voltage was subsequently decreased from max MM to a specific value of m, the t value was found and taken again. This t ,m value was subtracted from the value just measured and the result was taken as a value of at this specific max FM GM , m point. It was found that the measured points MFM max max , resemble a smooth curve, and the measured points ,, , mG M m FM resemble a smooth surface. Hence max was represented by a polynomial max 23 01max2 max3 max4max FM bbMbMbMbM 4 2 (15) And was represented by a trend surface ,GMm 2 12 345 232 2 678 9 343 2 1011 1213 34 14 15 ,GM mppmpMpmpMm pMpmpMmpM m pMpmpMm pMm pMm pM (16) Then the values of the parameters in Equations (15) and (16) were estimated by using the maximum like- lihood method based on the measurements of max FM and ,GMm. The estimated parameter values are shown in Table 1. With these parameters, the RI hysteresis of the actuators can be evaluated for any given input ut by using Equations (10) and (11). 4.4. Creep Sub-Model Parameter Estimation Creep is a slow effect. To identify the parameters involved in the creep sub-model, a step voltage input of 30V was applied to the PEA for an extended period of time (30 s). The output displacement t of the PEA was measured. And the corresponding 1 t was obtained by simula- tion using the identified hysteresis and vibration sub-mo- dels. Then 2 t, which is the measured output of 2 Gs Table 1. Estimated values of the parameters in Equations (15) and (16). Par. Value Par. Value Par. Value b0 4.84 3 p 2.85 × 106 10 p 362 b1 –745 4 p2.26 × 104 11 p 4.58 b2 5.50 × 104 5 p –3.35 × 104 12 p –9.67 b3 2.85 × 106 6 p 3.01 × 103 13 p 5.17 4 b 5.75 × 104 7 p 46.7 14 p 1.66 1 p 9.10 × 105 8 p –49.0 15 p –3.03 2 p –2.77 × 106 9 p –178 in Figure 5 induced by the input 1 t, was obtained by 21 txtxt . By using the System Identification Toolbox in MATLAB, an ARX (Auto Regressive with eXogenous input) model with a sampling period of 0.1 s and having 4 poles, 1 zero, and 1 sampling period of de- lay between output and input was identified by the least squares method to model creep. This ARX model was then converted into a continuous-time model as 32 2432 0.18044.18147.849.404 14.10610.11018 125.0 sss Gs sss (17) The simulated (by using Equation (17)) and the mea- sured creep displacements of the PEA are compared in Figure 7. 4.5. Validation of the Model of PEA The input voltage ut used for validating the integrated model of PEA is shown in Figure 8. In the experiments, 1v T was set to 50, 100, 200, 300, 400, and 500 Hz. Two of the measured results are shown in Figure 9; along with the simulation results obtained form the de- veloped model, for the purpose of comparison. The root- mean-square (RMS) errors and the maximum errors cal- culated over two periods of the waveform are given in Table 2. ut It can be seen from Figure 9 and Tabl e 2 that the PEA model integrating the RI hysteresis model with the vibra- tion and creep sub-models can represent the dynamics of the PEA with good accuracy (the RMS error is less than 1% of the maximum displacement of the PEA) when the PEA is subject to voltage input signals with a frequency up to 400 Hz. The increase in the RMS error as the input frequency increases is considered as a result of the un- modeled high-frequency dynamics of the PEA. The higher Figure 7. Measured and simulated creep displacements. Figure 8. u(t) used for PEA model validation. Copyright © 2011 SciRes. MME  J. Y. PENG ET AL. Copyright © 2011 SciRes. MME 30 is specifically designed to enable the representation of the one-sided hysteresis behavior. The resultant model of PEAs was validated through experiments. And it is con- cluded that the resultant model developed is capable of representing the dynamic behaviors of PEAs, including one-sided hysteresis, creep, and vibration dynamics ac- curately, with an RMS error less than 1% of the maxi- mum PEA displacement and in operations with frequent- cies up to 400 Hz. 6. Acknowledgements Financial support from the Natural Science and Engi- neering Research Council (NSERC) of Canada to the present study is acknowledged. Figure 9. PEA model validation. Table 2. Errors in the PEA model validation experiments. 7. References v T/1 (Hz) RMS Error (μm) Maximum Error (μm) 50 0.093 0.212 100 0.066 0.157 200 0.055 0.127 300 0.059 0.136 400 0.095 0.252 500 0.188 0.593 [1] S. Devasia, E. Eleftheriou and S. O. R. Moheimani, “A Survey of Control Issues in Nanopositioning,” IEEE Trans- actions on Control Systems Technology, Vol. 15, No. 5, 2007, pp. 802-823. doi:10.1109/TCST.2007.903345 [2] D. Croft, G. Shed and S. Devasia, “Creep, Hysteresis, and Vibration Compensation for Piezoactuators: Atomic Force Microscopy Application,” Journal of Dynamic Systems, Measurement, and Control, Vol. 123, No. 1, 2001, pp. 35-43. doi:10.1115/1.1341197 [3] J. Y. Peng and X. B. Chen, “Hysteresis Models Based on a Novel Hysteresis Unit,” 2011, Unpublished. RMS errors in the low frequency compared with those at medium are thought to be caused by the 2nd-order ap- proximation of the vibration dynamics that leads to a smal- ler phase lag then reality. [4] I. Mayergoyz, “Mathematical Models of Hysteresis,” Physical Review Letters, Vol. 56, No. 15, 1986, pp. 1518- 1521. doi:10.1103/PhysRevLett.56.1518 [5] P. Ge and M. Jouaneh, “Generalized Preisach Model for Hysteresis Nonlinearity of Piezoceramic Actuators,” Pre- cision engineering, Vol. 20, No. 2, 1997, pp. 99-111. doi:10.1016/S0141-6359(97)00014-7 5. Conclusions Accurate models of PEAs are highly desirable for both better understanding the behavior of such actuators and controller design. Such models can usually be constructed by cascading three sub-models together, each represent- ing the RI hysteresis, the vibration dynamics, and the creep effect, respectively. While the vibration dynamics and the creep effect have been accurately modeled in the literature, there are still problems concerning the model- ing of RI hysteresis. Traditionally, the CP hysteresis model has been widely used to represent the RI hysteresis in PEAs. However, it is found that the CP hysteresis model is incapable of representing the one-sided hysteresis be- havior in PEAs since it cannot represent the initial as- cending curve, inducing significant inaccuracy. To solve this problem, in this paper, an integrated model of PEAs as developed based on a new RI hysteresis model which [6] H. Hu and R. Ben-Mrad, “On the Classical Preisach Model for Hysteresis in Piezoceramic Actuators,” Mecha- tronics, Vol. 13, No. 2, 2002, pp. 85-94. doi:10.1016/S0957-4158(01)00043-5 [7] G. Song, J. Zhao, X. Zhou and J. A. De Abreu-García, “Tracking Control of a Piezoceramic Actuator with Hys- teresis Compensation Using Inverse Preisach Model,” IEEE/ASME Transactions on Mechatronics, Vol. 10, No. 2, 2005, pp. 198-209. doi:10.1109/TMECH.2005.844708 [8] X. Yang, W. Li, Y. Wang and G. Ye, “Modeling Hystere- sis in Piezo Actuator Based on Neural Networks,” Lec- ture Notes in Computer Science, Vol. 5370, 2008, pp. 290-296. doi:10.1007/978-3-540-92137-0_32 [9] X. B. Chen, Q. Zhang, D. Kang and W. Zhang, “On the Dynamics of Piezoactuated Positioning Systems,” Review of Scientific Instruments, Vol. 79, No. 11, 2008, pp. 116101- 1 to 116101-3. w
|