International Journal of Geosciences, 2011, 2, 573-584
doi:10.4236/ijg.2011.24060 Published Online November 2011 (http://www.SciRP.org/journal/ijg)
573
Rubber Tree Distribution Mapping in Northeast Thailand
Zhe Li1,2, Jefferson M. Fox2
1Agriculture and Agri-Food Canada, Ottawa, Canada
2East-West Center, Honolulu, USA
Received July 12, 2011; revised August 25, 2011; accepted September 29, 2011
Abstract
In many parts of mainland Southeast Asia rubber plantations are expanding rapidly in areas where the crop
was not historically found. Monitoring and mapping the distribution of rubber trees in the region is necessary
for developing a better understanding of the consequences of land-cover and land-use change on carbon and
water cycles. In this study, we conducted rubber tree growth mapping in Northeast Thailand using Landsat 5
TM data. A Mahalanobis typicality method was used to identify different age rubber trees. Landsat 5 TM 30
m non-thermal reflective bands, NDVI and tasseled cap transformation components were selected as the
model input metrics. The validation was carried out using provincial level agricultural statistical data on the
rubber tree growth area. At regional (Northeast Thailand) and provincial scales, the estimates of mature and
middle-age rubber stands produced from 30 m Landsat 5 TM data compared well (high statistical signifi-
cance) with the provincial rubber tree growth statistical data.
Keywords: Northeast Thailand, Rubber Tree Mapping, Land-Use and land-Cover Change, Mahalanobis
Typicality, Kauth-Thomas Transformation, Landsat 5 TM
1. Background
Around the world regional and global markets are driving
the conversion of traditional agriculture and occupied
non-agricultural lands to more permanent cash crops. In
many parts of mainland Southeast Asia rubber plantations
are expanding rapidly in areas where the crop was not
historically found [1]. Over the last several decades more
than 1,000,000 hectares of land have been converted to
rubber plantations in non-traditional rubber growing
areas of China, Laos, Thailand, Vietnam, Cambodia and
Myanmar [2,3]. Like many mainland Southeast Asian
countries, Thailand has experienced dramatic social and
environmental change over the past decade [4]. North-
east Thailand is a semi-arid [5] and chronically undeve-
loped area, and is a non-traditional rubber growing
region of Thailand (Figure 1). Rubber tree development
in this region has been booming for the past two decades.
To encourage farmers from leaving home to find jobs in
other parts of the country, this region is being targeted by
the Thai government to grow more rubber trees in the
next decade. The expansion of rubber trees has altered
the ecosystem by influencing local energy, water and
carbon fluxes, especially when rubber trees replaced eco-
logically important secondary forests and traditionally
managed swidden fields [6-9]. Timely monitoring and
mapping rubber tree growth distribution in the region is
critical for documenting its expansion and understanding
its implications for water and carbon dynamics.
2. Introduction
Remotely sensed imagery classification for deriving
land-use/cover information is well documented and plays
an important role in global-change studies, natural re-
source management and environmental applications. A
number of studies of the distribution of rubber tree
growth have been conducted in Southeast Asia, such as
in Yunnan, China [7,8,10], Indonesia [11] and Laos [12].
Most spatial analysis of rubber trees has been limited to
suitability analyses in Thailand (e.g. [13]). Land-cover
mapping over large areas with limited training samples is
challenging due to the capability of classifiers to gener-
alize patterns in unsampled areas. Analysts attempting to
map rubber tree growth face two significant challenges.
First, mature rubber trees are easily confused with tropi-
cal evergreen vegetation due to similar multi-spectral
reflectance characteristics. Area of mature rubber trees is

Z. LI ET AL.
574
Figure 1. Map of Northeast Thailand.
often overestimated by misclassifying secondary forests
as rubber trees. Second, young rubber trees are usually
dominated by bare ground and mixed scrub, or inter-
cropped with short-term economic crops such as cassava
and pineapple. Even after 3 - 4 years of growth, rubber
tree canopies comprise a small fraction of total planted
area. These conditions make it difficult to map rubber
trees.
Recently machine learning techniques [14] such as ar-
tificial neural networks and decision tress [15] have been
widely used in remotely sensed imagery classification
because they show many advantages over conventional
classifiers [16-18]. However, the substantial computation
time and heuristic training process of machine learning
classifiers make rubber tree growth mapping over large
areas inefficient. Experiments conducted by Li and Fox
[19] suggest that using approaches of neural networks
and decision trees with spectral information and vegeta-
tion indices overestimated the number of rubber tree pix-
els. Additionally, these classifiers require training sites to
contain sufficient both “presence” and “absence” infor-
mation. In other words, the analyst must acquire such
information from the training samples. In reality, it is
difficult to collect sufficient training samples in the field
to cover the numerous patterns of rubber tree stages that
show up in an analysis. Given this fact, a presence-data-
only model looks increasingly promising in dealing with
species distribution mapping, especially when knowl-
edge about available land-cover types is limited. Sanger-
mano and Eastman [20] and Hernandez et al. [21] con-
ducted experiments using a presence-data-only model –
Mahalanobis typicality approach to model species dis-
tribution, as Mahalanobis typicalities provide informa-
tion about how typical instances being analyzed are
compared to those used as a reference [20].
Selection of satellite images is another critical step for
mapping of land-cover. Given the trade-off between spa-
tial and temporal resolutions, currently selection of re-
motely sensed data for land-cover mapping at a global or
a regional scale tends to use either low spatial but high
temporal resolution imagery, such as Moderate Resolu-
tion Imaging Spectro-radiometer (MODIS) (e.g. [22]), or
low temporal but high spatial resolution imagery such as
Landsat Thematic Mapper (TM)/Enhanced Thematic
Mapper (ETM+), etc. [23-27]. Li and Fox [28] improved
rubber tree growth mapping using ASTER data by inte-
grating Mahalanobis typicalities with a neural network
model. Another successful application using Mahalano-
bis typicality approach was the mapping of rubber trees
across the mainland Southeast Asia using the Mahala-
nobis typicality method with MODIS time-series NDVI
and statistical data [19]. In this study we examined the
potential of Mahalanobis typicalities for rubber tree
growth distribution mapping using Landsat 5 TM imagery.
3. Study Area and Data
The study area encompasses nineteen provinces of Nor-
theast Thailand as shown in Table 2 and Figure 1. The
Landsat 5 TM imagery used in this study was acquired
from Land Processes Distributed Active Archive Center
(LPDAAC). Eleven TM scenes (WRS Path/Row:
126-129/47-50) were used to cover the entire study area.
The acquisition dates of the images vary from 2004 to
2009, depending upon the availability of cloud free or
acceptable cloud contamination images. To develop
training sites for calibrating the classifiers, we used
NASA’s Landsat GeoCover products (http://www.geo-
cover.com/gc_lc/data_products/) to identify land-use and
land-cover types. Rubber tree identification was primar-
ily based on GPS ground truthing samples collected in
the field in January and March 2009 and high resolution
QuickBird / IKONOS images from Google Earth. Since
the main purpose of this experiment was to map rubber
tree growth distribution, only six broad categories were
identified for the study region, i.e., rubber trees, forest,

Z. LI ET AL.
575
water, bare soil, paddy rice and others. Three sub-cate-
gories were defined for the rubber tree class: 1) Rubber 1,
mature rubber trees older than 4 years old; 2) Rubber 2,
middle-age rubber trees between 2 to 4 years old; and 3)
Rubber 3, young rubber trees less than 2 years old domi-
nated by bare ground and mixed scrub, or intercropped
with other crops. Figure 2 shows photographs of dif-
ferent age rubber stands under various situations. Train-
ing sites comprising a total of 85,697 rubber tree samples
were developed, accounting for 0.046% of the total study
area. Among those samples, 67,839 were of mature rub-
ber trees, 12,770 were of middle-age rubber trees, and
5088 were of young rubber trees, accounting for 0.037%,
0.007% and 0.003% of the total study area respectively
(Table 1).
Rubber tree growth statistical data provided by the
Thai Rubber Association (http://www.thainr.com/en/in-
dex.php?detail=stat-thai&page=1#) estimated rubber tree
growth area and production between 2005 and 2007 at
the provincial scale. Provincial and international bounda-
ries were extracted from a Thailand vector GIS layers for
Figure 2. Different age rubber trees: (a) Rubber trees more
than 7 years old (tapping); (b) Rubber trees between 4 and
7 years; (c) Rubber trees less than 4 years old dominated by
bare soil; (d) Rubber trees less than 4 years old inter-
cropped with cassava; (e) Rubber trees less than 4 years old
intercropped with pineapple; and (f) Rubber trees less than
4 years old mixed with fallow weeds. (Source: Li and Fox
[19], 2011)
validating the statistical data.
4. Methods
4.1. Image Pre-Processing
Atmospheric correction using Chavez’s Cost model was
applied to the TM images to reduce atmospheric scat-
tering effects [29,30]. The TM images were
geo-metrically corrected using the Landsat GeoCover
data set and the nearest neighborhood resampling
method [31]. All images were co-registered to the UTM
system (zone 48 N). Clouds and shadows were masked
out from the images.
4.2. Development of Input Metrics
The Normalized Difference Vegetation Index (NDVI), a
frequently used measure of photosynthetic activity to
estimate productivity [32], is sensitive to canopy struc-
ture and chemical content [33]. In this study, Landsat
TM NDVI was derived from TM band 4 and band 3, to
capture general patterns of different vegetation types.
The NDVI formula we used was:
Band4 Band3
NDVI Band4 Band3

 (1)
The Kauth-Thomas Transformation (KTT or tasseled
cap transformation) [34,35] has been found to be sensi-
tive to structural characteristics of forest environments
[35,36]. To highlight spectral difference among stands of
different age rubber trees, e.g., mature, middle and young,
as well as that among rubber trees and deciduous forest,
shrubs and bare soil etc., we employed KTT on the six
reflective TM bands to produce soil brightness, vegeta-
tion greenness, and soil/vegetation wetness components.
The vegetation greenness component is well correlated
with tree canopy cover, leaf area index and live biomass
above ground [37]; therefore it was expected to be able
to capture difference among stands of rubber trees of
diverse ages due to differences in canopy densities. The
soil brightness component expresses differences in soil
properties, such as particle size and organic matter con-
tent; and the soil/vegetation wetness component is sensi-
tive to soil and plant moisture [37]. These two compo-
nents together were expected to capture difference be-
tween young rubber trees (dominated by bare soil or
shrubs) and pure bare soil fallow fields. The KTT equa-
tions [41] we used were:
TM Bright = TM1 × 0.3037 + TM2 × 0.2793 + TM3
× 0.4343 + TM4 × 0.5585 + TM5
× 0.5082 + TM7 × 0.1863

Z. LI ET AL.
576
TM Green = TM1 × (–0.2848) + TM2 × (–0.2435)
+ TM3 × (–0.5436) + TM4 × 0.7243
+ TM5 × 0.0840 + TM7× (–0.1800)
TM Moist = TM1 × 0.1509 + TM2 × 0.1793 + TM3
× 0.3299 + TM4 × 0.3406 + TM5
× (–0.7112) + TM7× (–0.4572) (2)
4.3. Mahalanobis Typicality
In statistics Typicality Probability can be expressed by
the relative distance of a particular class to the class
mean, i.e., Mahalanobis distance [38-40]:

1
T
ii i
D  xμVx
μ
(3)
where x is the input variable vector (from the context of
remote sensed imagery, x is the data vector for the pixels
in all wavebands), μi is the mean vector for class i over
all pixels, Vi is the variance/covariance matrix for class i,
and T is the transpose of the matrix .
Ranging from 0 to 1, the Mahalanobis typicality meas-
ures the absolute strength of class membership [40] and
determines the similarity of an unknown sample to a
known group of samples. A typicality value of 0 indi-
cates the instance being analyzed is atypical of the refer-
ence samples, while a value of 1 suggests the instance is
identical to the known samples. Therefore, typicality
values express how reasonable to assume a case really
belongs to a particular class. In the context of remotely
sensed imagery classification, the outputs of Mahalano-
bis typicalies are a set of probability images (one per
class) that express the typicality of each pixel relative to
the training samples. Because a Mahalanobis typicality
calculates an intra-class similarity, it can use presence-
only data and is not affected by absence-data. For more
detailed description of Mahalaanobis Typicality, see
Eastman [41] (2009) and Sangermano and Eastman [20].
4.4. Classification and Image Post-Processing
Since TM scenes acquired in succession on the same
track (with the same path numbers) are of more consis-
tency in terms of the radiometry, we mosaiced the TM
scenes with the same path numbers to spatially produce
larger images. Separate training sites were developed for
each of the mosaiced images. Four mosaiced images
were made to cover the whole study area. Each larger
mosaiced image was processed individually for land-
cover classification.
Six TM reflective bands (1-5 and 6), NDVI, and the
greenness, brightness and the moistness from the KTT
were developed for each mosaiced image and used as
input variables to the Mahalanobis distance classifier.
Unlike traditional hard classifiers, the output from the
Mahalanobis distance classifier is not a single classified
land-cover map, but rather, a set of images (one per class)
that expresses typicality of pixel reflectances relative to
those described by the training sites. In our case study,
eight Mahalanobis typicality maps were generated rep-
resenting the typicality probabilities for each of the eight
categories (Table 1). Since we are interested in the dis-
tribution of rubber tree growth, only the rubber tree
classes, e.g, mature, middle-age, and young were ana-
lyzed and the rest of five classes were ignored. To reduce
commission errors of rubber trees (i.e., the probability
that a sample from a land-cover map is misclassified
against what it is from the reference data) only pixels
that were most typical of the rubber tree classes de-
scribed by the training sites were retained. To do this, we
set typicality thresholds of 0.94 - 0.97 for both mature
and middle-age rubber trees, and 0.99 for young rubber
trees. These thresholds were determined based on the
best calibration of the classifier using our training sites.
The threshold set for the young rubber trees (0.99) is
more restricted than those for mature and middle-age
rubber trees because young rubber trees are highly likely
to be confused with bare soil or fallow fields after plow-
ing. A discrete map of rubber tree growth (Boolean map)
was extracted by thresholding the typicality values for
each type of rubber trees. However, the rubber tree
growth map created this way scattered rubber trees into
small patches because the high typicality thresholds fil-
tered out pixels with lower typicalities even when they
neighbor “most typical” pixels and actually do belong to
a rubber tree category. To overcome this drawback, we
used 11 × 11 sized mean filters to retrieve neighboring
pixels excluded by the Mahalanobis typicality. Again,
thresholds were set adaptively with the filtered images
for each of the three types of rubber trees based on the
best calibration using the same training site information.
Table 1. Number of land-cover training samples for North-
east Thailand.
Class
ID Class Number of Pixels (cell)
Proportion
(%)
1 Mature rubber trees (>4 years) 67,839 0.037
2 Middle-age rubber trees (2 - 4 years) 12,770 0.007
3 Young rubber trees (<2 years) 5088 0.003
Subtotal 85,697 0.046
4 Bare soil 18,278 0.010
5 Paddy 35,438 0.019
6 Forest 6,723,175 3.622
7 Water 394,528 0.213
8 Others 42,579 0.023
Total 7,299,695 3.932

Z. LI ET AL.
577
The final rubber tree growth map was generated by over-
laying the three types of rubber tree maps. The class
membership of ambiguous pixels such as those classified
as rubber trees in more than one of the three types of
rubber tree growth maps were determined by assigning
each pixel to the class where it had its highest typicality
statistic. The selected filters were able to generalize the
image and exclude isolated misclassified rubber tree pix-
els, thus the filtered images retain both map accuracy and
the spatial connectivity of the rubber tree classes.
4.5. Validation
The output rubber tree growth map for Northeast Thai-
land created from the TM images estimates rubber tree
growth area by pixel. The total area of rubber trees was
then extracted to the provincial level. The results were
compared with provincial level statistical data from
Thailand collected between 2005 and 2007. The relative
error (RE) was used to evaluate the accuracy of the esti-
mated rubber tree area for each province in Northeast
Thailand, i.e.,
RE = (Estimated – Statistics)/Statistics × 100 (4)
Linear regressions were employed between the statis-
tical data and the estimates (30 m Landsat TM data) for
validation [22]. The root mean square error (RMSE) was
calculated between the statistical values and estimates for
the study area using the following equation:

2
1
RMSEStatisticsEstimated
n
i
n


 (5)
where n is the number of provinces in Northeast Thai-
land.
Areas of different age rubber trees were compared
between the estimated and statistical data. The follow-
ing area indices were calculated from the statistical
data:
A
m 2006 = At 2006 – Ah 2006 – An 2006
An 2006 = At 2006 – At 2005 (6)
where
Ah 2006: Area of tapped rubber trees (>7 years old) in
2006
Am 2006: Area of middle-age rubber trees (2 - 7 years
old)
An 2006: Area of new rubber trees (less than 2 years old)
planted in 2006
At 2006: Total area of rubber trees planted in 2006
At 2005: Total area of rubber trees planted in 2005
Due to different age groups defined in the rubber tree
growth classification (i.e., <2, 2 - 4 and >4 years old), the
estimated areas of the classified rubber trees from the
satellite imagery were not directly comparable with those
from the statistical data (i.e., <2, 2 - 7 and >7 years old).
Conversions were needed for the estimated results to
make them consistent with the statistical data. To do this,
the area of the mapped rubber tree growth that is equiva-
lent to 2 - 7 years old as defined in the statistical data
(Am 2006) was approximated using the following equation:
Estimated Am 2006 = 0.4 × ARubber1 + ARubber2 (7)
where ARubber1 and ARubber2 are areas of Rubber1 and
Rubber 2, which were defined as more than 4 years old
and between 2 and 4 years old, respectively.
5. Results and Discussion
Figure 3 is a rubber tree growth map generated from the
TM imagery showing mature, middle-age, and young
rubber trees for Northeast Thailand. Tables 2 and 3
compare the estimated rubber tree area versus the statis-
tical data.
Rubber tree growth estimates in most of the nineteen
provinces in Northeast Thailand were based on TM im-
ages acquired in 2006, but data from Ubon Ratchathani
province were from a 2009 image, because it was the
best cloud-free image available covering this region.
Sakon Nakhon and Nakhon Phanom provinces were
based on 2007 images, and Nong Khai and Kalasin were
covered by multiple images ranging from 2004 to 2007
(Table 2). The estimated rubber tree area for each prov-
ince from the TM imagery actually reflected total area of
rubber trees planted in a particular province as of the
acquisition date(s) of the image(s). For example, Nong
Khai province is covered by three TM scenes acquired
from three different dates of 2004, 2006 and 2007. To
reasonably validate the estimated rubber tree area, we
used adjusted statistical data instead of the statistical data
from each year, e.g., for Nong Khai, the validation was
based on the average of rubber tree growth areas in 2004,
2006 and 2007. Similarly adjusted statistical data were
used for the other provinces. For Ubon Ratchathani
province, although time is asynchronous between the
statistical data (2007) and Landsat 5 TM image (2009)
(Table 2), it is reasonable to see that the area estimated
from the latter is higher than the actual area from the
former, which may indicate an increase of rubber plant-
ing area during the two years.
5.1. Total Rubber Tree Growth Area
The relative errors (RE) shown in Table 2 provides in-
formation about the accuracy of rubber tree growth area
estimates for each province. Results indicate that the
estimated area of rubber trees for most provinces is con-

Z. LI ET AL.
578
Figure 3. Landsat TM estimated rubber tree distribution in Northeast Thailand for 2004-2007. Numbers 1 - 19 represent the
19 provinces listed in Table 2.
sistent with the adjusted statistical data except in four
provinces, Maha Sarakham, Nakhon Ratchasima, Sakon
Nakhon and Khon Kaen. Estimates for ten of the nine-
teen provinces performed well with REs below one third,
and five of which performed very well with REs below
16%, including Nong Khai, Kalasin, Udon Thani, Ubon
Ratchathani and Mukdahn. The ratio of RMSE to the
statistical data for all the nineteen provinces was only
2.89%. Figure 4(a) illustrates per province rubber tree
growth area comparison between the Landsat estimate
and the adjusted statistical data. The regression of rubber
tree growth area at the provincial level was statistically
significant (y = 1.0008x + 702.4; R2 = 0.774; p ≤ 0.001).
When the three provinces with the highest REs (i.e.,
Maha Sarakham, Nakhon Ratchasima, Sakon Nakhon)
were excluded from Table 2, the ratio of RMSE to the
statistical data of the estimated rubber tree growth area
for the sixteen provinces decreased to 2.08%, and R2 for
the regression line increased to 0.9106 (y = 1.0471x +
2006.1; R2 = 0.91; p ≤ 0.001) (Figure 4(b)). The total
area of rubber tree growth for the sixteen provinces was
underestimated by 21,800 ha, which was less than 10%.
The following analysis and validation is based on data
from these sixteen provinces.
5.2. Mature Rubber Trees
The Landsat classification map defined mature rubber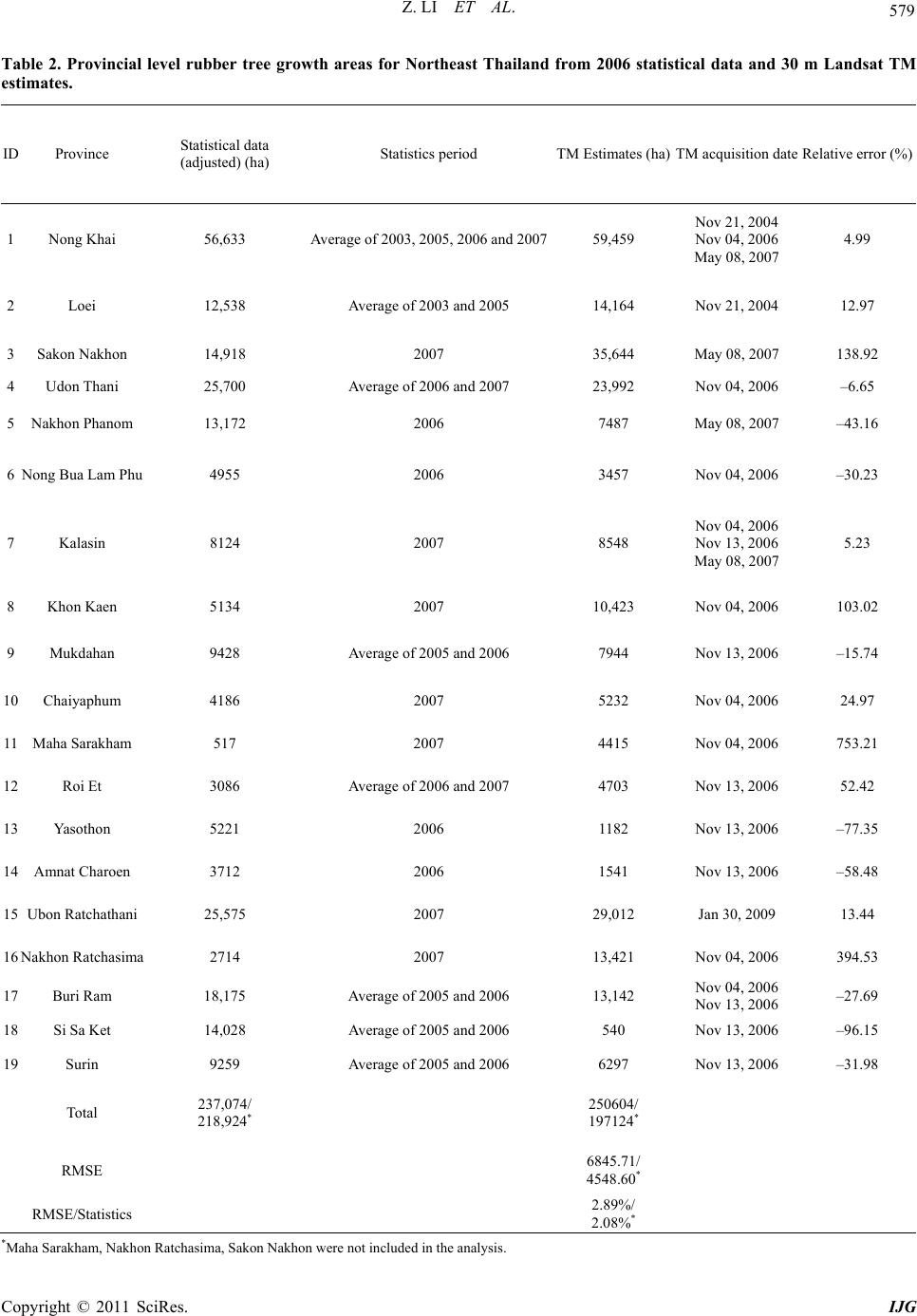

Z. LI ET AL.
579
Table 2. Provincial level rubber tree growth areas for Northeast Thailand from 2006 statistical data and 30 m Landsat TM
estimates.
ID Province Statistical data
(adjusted) (ha) Statistics period TM Estimates (ha)TM acquisition date Relative error (%)
1 Nong Khai 56,633 Average of 2003, 2005, 2006 and 200759,459
Nov 21, 2004
Nov 04, 2006
May 08, 2007
4.99
2 Loei 12,538 Average of 2003 and 2005 14,164 Nov 21, 2004 12.97
3 Sakon Nakhon 14,918 2007 35,644 May 08, 2007 138.92
4 Udon Thani 25,700 Average of 2006 and 2007 23,992 Nov 04, 2006 –6.65
5 Nakhon Phanom 13,172 2006 7487 May 08, 2007 –43.16
6 Nong Bua Lam Phu 4955 2006 3457 Nov 04, 2006 –30.23
7 Kalasin 8124 2007 8548
Nov 04, 2006
Nov 13, 2006
May 08, 2007
5.23
8 Khon Kaen 5134 2007 10,423 Nov 04, 2006 103.02
9 Mukdahan 9428 Average of 2005 and 2006 7944 Nov 13, 2006 –15.74
10 Chaiyaphum 4186 2007 5232 Nov 04, 2006 24.97
11 Maha Sarakham 517 2007 4415 Nov 04, 2006 753.21
12 Roi Et 3086 Average of 2006 and 2007 4703 Nov 13, 2006 52.42
13 Yasothon 5221 2006 1182 Nov 13, 2006 –77.35
14 Amnat Charoen 3712 2006 1541 Nov 13, 2006 –58.48
15 Ubon Ratchathani 25,575 2007 29,012 Jan 30, 2009 13.44
16 Nakhon Ratchasima 2714 2007 13,421 Nov 04, 2006 394.53
17 Buri Ram 18,175 Average of 2005 and 2006 13,142 Nov 04, 2006
Nov 13, 2006 –27.69
18 Si Sa Ket 14,028 Average of 2005 and 2006 540 Nov 13, 2006 –96.15
19 Surin 9259 Average of 2005 and 2006 6297 Nov 13, 2006 –31.98
Total 237,074/
218,924* 250604/ 197124*
RMSE 6845.71/
4548.60*
RMSE/Statistics 2.89%/
2.08%*
*Maha Sarakham, Nakhon Ratchasima, Sakon Nakhon were not included in the analysis.

Z. LI ET AL.
580
Table 3. Provincial area of different age rubber trees for Northeast Thailand from 2006 statistics and 30 m Landsat TM
estimates (Thai Rubber Association, http://www.thainr.com/en/index.php?detail=stat-thai&page=1#).
Province
Estimated Rub
b
er
1 (>4 years old)
(ha)
Estimated Rub
b
er
2 (2 - 4 years old)
(ha)
Estimated Rub
b
er
3 (<2 years)
(ha)
Approximated
rubber trees
(2 - 7 years)
Tapped rubber
trees** Ah 2006
(ha)
Middle-aged
rubber trees
Am 2006 (ha)
New planted
rubber trees
An 2006 (ha)
Nong Khai 48,355 10,327 777 29,669 15,848 26,013 27,100
Loei 14,164 0 0 5666 5212 12,068 13,886
Sakon Nakhon
Udon Thani 22577 1288 127 10,319 7910 5112 3536
Nakhon Phanom 3840 3447 200 4983 4458 4094 4620
Nong Bua Lam Phu 2936 513 8 1687 953 2925 1077
Kalasin 7629 857 63 3908 3023 1924 721
Khon Kaen 7870 2507 46 5655 1258 841 974
Mukdahan 7881 54 9 3206 3080 4505 2826
Chaiyaphum 4718 504 9 2391 1068 640 1274
Maha Sarakham
Roi Et 4703 0 0 1882 1598 627 550
Yaosothon 1182 0 0 473 1552 2609 1060
Amnat Charoen 73 1112 356 1141 327 2325 1060
Ubon Ratchathani 3066 19,931 6016 4584 7281
Nakhon Ratchasima
Buri Ram 11,649 1417 75 6077 8484 4566 7692
Si Sa Ket 234 241 64 335 5388 5292 5854
Surin 6269 27 1 2535 3576 4323 2053
Total 147,146 42,225 7753 79,926 68,320 77,863 81,563
*Sakon Nakhon, Maha Sarakham, Nakhon Ratchasima were not included in the analysis; **multiple-year statistical data were adjusted.
trees as rubber trees more than four years old; this class
covered a wider range than that represented by tapped
rubber trees from the statistical data, as latex is generally
collected from rubber trees that are more than 7 years old.
It is thus expected that the area of mapped mature rubber
trees should be greater than that of Tapped rubber trees.
Figure 5 shows that the area of estimated mature rubber
trees (rubber trees more than 4 years old) is significantly
correlated (R2 = 0.7766; p ≤ 0.001) with the area of har-
vested rubber trees at the provincial level (16 provinces),
and the estimated area of mature rubber trees is ap-
proximately 2 - 3 times more than tapped rubber trees.
5.3. Middle-Age Rubber Trees
Figure 6 illustrates that the area of rubber trees between
two to seven years old for fifteen provinces (Ubon
Ratchathani not included) approximated by the estimated
area from Landsat using Equation (7) is consistent with
that estimated from the statistical data. The two sets of
data are significantly correlated (R2 = 0.7911; p ≤ 0.001)
and the estimated area (79,926 ha) and statistics area
(77,863 ha) are equivalent (see Table 3). This suggests
that the area of middle-age rubber trees can be reasona-
bly reflected through the satellite imagery although the
mapped rubber tree growth has different age structure
with the statistical data.
5.4. Young Rubber Trees
Mapping of young rubber tree growth has been difficult
for researchers as young rubber trees are often dominated
by diverse ground conditions. The estimate of the area of
young rubber trees was not as satisfactory as those for
mature and middle-age rubber trees. Table 3 shows the
area of newly planted rubber trees in 2006 for the sixteen
provinces versus the estimated area from the Landsat
data. Results indicate that young rubber trees were only
closely estimated for Ubon Ratchathani (6016 ha versus
7281 ha from the statistical data), and remotely sensed
based estimates of rubber tree growth area underesti-
mated young rubber trees in all other provinces. This is
because when using the Mahalanobis typicality method,
only the pixels that are most typical of young rubber tree
samples encountered in the training sites are retained.
Those pixels that are less “typical” of training samples
are screened out by the thresholds determined by the
amount of rubber trees in each province. Figure 8(a)

Z. LI ET AL.
581
(a)
(b)
Figure 4. Estimated total area of rubber trees versus that
from the adjusted statistical data for (a) 19 provinces (p ≤
0.001) and (b) 16 provinces (p ≤ 0.001) of Northeast Thai-
land in 2006.
shows no correlation (R2 = 0.034; p = 0.497) between the
estimated and statistical data sets. However, when only
looking at thirteen out of sixteen provinces (i.e., remov-
ing Loei, Amnat Charoen and Nakhon Ratchasima), the
estimated area of young rubber trees shows the same
trend with that from the statistical data; there was a sig-
nificant correlation (R2 = 0.9106; p ≤ 0.001) between
these data sets (Figure 8(b)). This suggests that the map-
ping accuracy would be expected to improve if more
young rubber tree training samples were included to rep-
resent a wider variability of this class (the available
training samples used for young rubber trees only ac-
Figure 5. Relationship between the estimated area of ma-
ture rubber trees (more than 4-years old) from Landsat TM
data and the area of tapped rubber trees (usually more
than 7-years) from the adjusted statistical data for North-
east Thailand (16 provinces) (p ≤ 0.001).
Figure 6. Estimated area rubber trees between 2 - 7 years
old from Landsat TM data versus that calculated from sta-
tistical data for Northeast Thailand (15 provinces) (p ≤
0.001) in 2006.
counted for 0.003% of the total study area). Figure 7
illustrates the total estimated area of tapped and young
rubber trees versus that calculated from the statistical
data. The two data sets are highly correlated (R2 = 0.8251;
p ≤ 0.001) but with a slope of 0.6479. This suggests that
the underestimate was mainly due to underestimating the
area of young rubber trees.
5.5. Multi-Regression Analysis
Multi-regression analysis of data from the sixteen prov-

Z. LI ET AL.
582
Figure 7. Estimated area of rubber trees more than 7 and
less than 2 years old versus the total area of rubber trees of
the same ages calculated from the statistical data for
Northeast Thailand (15 provinces) in 2006 (p ≤ 0.001)
inces was conducted on the dependent variable, total area
of rubber tree growth for each province from the adjusted
statistical data, against the three independent variables,
estimated areas of mature rubber trees (AR1), middle-age
rubber trees (AR2) and young rubber trees (AR3). The re-
gression equation is listed as follow:
Rubber_Area_statistics = 0.844 × AR1 + 1.19 × AR2 – 0.58
× AR3 + 3057.626
The regression is significant (p ≤ 0.001) with R2 =
0.913 and adjusted R2 = 0.892. This result indicates that
the total area of rubber tree growth from the statistical
data was well estimated by the Landsat TM data.
6. Summary and Conclusions
Rubber tree growth mapping using 30 m Landsat TM
data was conducted for Northeast Thailand with a very
limited number of training samples. The Mahalanobis
typicality method was used to identify different age rub-
ber stands. Sixteen out of nineteen provinces were se-
lected for final statistical analysis and validation. The
validation was carried out using provincial level statisti-
cal data. Several conclusions can be drawn from this
study. First, the Mahalanobis distance based typicality
model successfully classified rubber stands that were
typical of known samples from the training sites and
overcoming the drawback of overestimation. Second,
NDVI and tasseled cap transformation components to-
gether with Landsat TM 30 m reflective bands were use-
ful in differentiating rubber trees from other vegetation
and crops. Third, at regional and province scales, the
(a)
(b)
Figure 8. Estimated area of young rubber trees (less than 2
years old) from Landsat TM data versus the area of new
rubber trees planted in 2006 from the statistical data for
Northeast Thailand, (a): for 16 provinces (p = 0.497); and
(b): for 13 provinces (p ≤ 0.001).
estimates of mature and middle-age rubber tree growth
areas using 30 m Landsat TM data were significantly
close to the provincial statistical data. Therefore the
typicality approach is a prominent and a robust means of
mapping species distribution with limited presence in-
formation. Improvements can be made to map young
rubber trees more accurately with more high-quality
training information for model calibration. Future work
will explore the usefulness of phenological factors for
enhancing rubber tree growth discrimination.

Z. LI ET AL.
583
7. Acknowledgements
This work was funded by NASA Earth System Science
grants NNG04GH59G and NX08AL90G, and Geo-In-
formatics and Space Technology Development Agency
of Thailand. We thank Dr. Roengsak Katawatin at Khon
Kaen University, Thailand for providing GIS lab and
support during our field work in Thailand, and thank Mr.
Dieuwe Da La Parra for his assistance with the field sur-
vey. We also thank Mr. John Vogler (formerly with East-
West Center) for developing and maintaining the geo-
spatial information database.
8. References
[1] J. Fox and J. Vogler, “Land-Use and Land-Cover Change
in Montane Mainland Southeast Asia,” Environmental
Management, Vol. 36, No. 3, 2005, pp. 394-403.
doi:10.1007/s00267-003-0288-7
[2] A. D. Ziegler, J. M. Fox and J. Xu, “The Rubber Jugger-
naut,” Science, Vol. 324, No. 5930, 2009, pp. 1024-1025.
doi:10.1126/science.1173833
[3] C. C. Mann, “Addicted to Rubber,” Science, Vol. 325, No.
5940, 2009, pp. 565-566. doi:10.1126/science.325_564
[4] S. J. Walsh, B. Entwisle, R. R. Rindfuss and P. H. Page,
“Spatial Simulation Modeling of Land Use/Land Cover
Change Scenarios in Northeastern Thailand: A Cellular
Automata Approach,” Journal of Land Use Science, Vol.
1, No. 1, 2006, pp. 5-28.
doi:10.1080/17474230600604213
[5] K. Watanabe, T. Yamamotob, T. Yamada, T. Sakuratani,
E. Nawata, C. Noichana, A. Sributta and H. Higuchi,
“Changes in Seasonal Evapotranspiration, Soil Water
Content, and crop Coefficients in Sugarcane, Cassava,
and Maize Fields in Northeast Thailand,” Agricultural
Water Management, Vol. 67, No. 2, 2004, pp. 133-143.
doi:10.1016/j.agwat.2004.02.004
[6] J. Xu, J. M. Fox, J. B. Vogler, P. Zhang, Y. Fu , L. Yang,
J. Qian and S. Leisz, “Land-Use and Land-Cover Change
and Farmer Vulnerability in Xishuangbanna Prefecture in
Southwestern China,” Environment Management, Vol. 36,
No. 3, 2005, pp. 404-413.
doi:10.1007/s00267-003-0289-6
[7] H. Li, Y. Ma, T. M. Aide and W. Liu, “Past, Present and
Future Land-Use in Xishuangbanna, China and the Im-
plications for Carbon Dynamics,” Forest Ecology and
Management, Vol. 255, No. 1, 2008, pp. 16-24.
doi:10.1016/j.foreco.2007.06.051
[8] H. Hu, W. Liu and M. Cao, “Impact of Land Use and
Land Cover Changes on Ecosystem Services in Menglun,
Xishuangbanna, Southwest China,” Environmental Moni-
toring and Assessment, Vol. 46, No. 1-3, 2008, pp. 147-
156. doi:10.1007/s10661-007-0067-7
[9] D. Lawrence, D. R. Peart and M. Leighton, “The Impact
of Shifting Cultivation on a Rainforest Landscape in
West Kalimantan: Spatial and Temporal Dynamics,”
Landscape Ecology, Vol. 13, No. 3, 1998, pp. 135-148.
doi:10.1023/A:1007985915187
[10] H. Li, T.M. Aide, Y. Ma and W. Liu, “Demand for Rub-
ber Is Causing the Loss of High Diversity Rain Forest in
SW China,” Biodiversity Conservation, Vol. 16, No. 6,
2007, pp. 1731-1745. doi:10.1007/s10531-006-9052-7
[11] A. Ekandinata, A. Widayati and G. Vincent, “Rubber
Agroforest Identification Using Object-Based Classifi-
cation in Bungo District, Jambi, Indonesia,” The 25th Asian
Conference on Remote Sensing, Chiang Mai, Thailand,
22-26 November 2004.
[12] K. Hurni, “Rubber in Laos: Detection of Actual and As-
Sessment of Potential Plantations in Lao PDR Using GIS
and Remote Sensing Technologies, Master Thesis,” Cen-
tre for Development and Environment, University of Bern,
Bern, 2008.
[13] E. Van Ranst, H. Tang, R. Groenemans and S. Sinthura-
hat, “Application of Fuzzy Logic to Land Suitability for
Rubber Production in Peninsular Thailand,” Geodema,
Vol. 70, No. 1, 1996, pp. l-19.
doi:10.1016/0016-7061(95)00061-5
[14] C. Bishop, “Pattern Recognition and Machine Lear-
ning,” Springer, New York, 2006.
[15] J. R. Quinlan, “Induction of Decision Trees. Machine
Learning, Vol. 1, No. 1, 1986, pp. 81-106.
doi:10.1007/BF00116251
[16] D. L. Civco, “Artificial Neural Networks for Land Cover
Classification and Mapping,” International Journal of
Geographical Information Science, Vol. 7, No. 2, 1993,
pp. 173-186. doi:10.1080/02693799308901949
[17] Z. Li and J. R. Eastman, “Commitment and Typicality
Measures for the Self-Organizing Map,” International
Journal of Remote Sensing, Vol. 31, No. 16, 2010, pp.
4265-4280. doi:10.1080/01431160903246725
[18] C. D. Lippitt, J. Rogan, Z. Li, J. R. Eastman and T. G.
Jones, “Mapping Selective Logging in Mixed Deciduous
Forest: A Comparison of Machine Learning Algorithms,”
Photogrammetric Engineering and Remote Sensing, Vol.
74, No. 10, 2008, pp. 1201-1211.
[19] Z. Li and J. M. Fox, “Mapping Rubber Tree Growth in
Mainland Southeast Asia Using Time-Series MODIS 250
m NDVI and Statistical Data,” Applied Geography, Vol.
32, No. 2, 2011, pp. 420-432.
doi:10.1016/j.apgeog.2011.06.018
[20] F. Sangermano and R. Eastman, “Linking GIS and Ecol-
ogy: The Use of Mahalanobis Typicalities to Model Spe-
cies Distribution,” In: G. D. Buzai, Eds., Memorias XI
Conferencia Iberoamericana de Sistemas de Información
Geográfica, Buenos Aires, 2007.
[21] P. A. Hernandez, I. Franke, S. K. Herzog, V. Pacheco, L.
Paniagua, H. L. Quintana, A. Soto, J. J. Swenson, C.
Tovar, T. H. Valqui, J. Vargas and B. E. Young, “Pre-
dicting Species Distributions in Poorly-Studied Land-
scapes,” Biodiversity and Conservation, Vol. 17, No. 6,
2008, pp. 1353-1366. doi:10.1007/s10531-007-9314-z
[22] J. Chang, M. C. Hansen, K. Pittman, M. Carroll and C.
Di-Miceli, “Corn and Soybean Mapping in the United

Z. LI ET AL.
584
States Using MODIS Time-Series Data Sets,” Agronomy
Journal, Vol. 99, No. 6, 2007, pp. 654-1664.
doi:10.2134/agronj2007.0170
[23] R. Katawatin, P. H. Crown and D. L. Klita, “Mapping
Dry Season Crops in Thailand Using Landsat-5 TM
Data,” Canadian Journal of Remote Sensing, Vol. 22, No.
4, 1996, pp. 349-472.
[24] A. J. W. De Wit and J. G. P. W. Clevers, “Efficiency and
Accuracy of Per-Field Classification for Operational
Crop Mapping,” International Journal of Remote Sensing,
Vol. 25, No. 20, 2004, pp. 4091-4112.
doi:10.1080/01431160310001619580
[25] M. A. Wulder, S. M. Ortlepp, J. C. White and S. Maxwell,
“Evaluation of Landsat-7 SLC-off Image Products for
Forest Change Detection,” Canadian Journal of Remote
Sensing, Vol. 34, No. 2, 2008, pp. 93-99.
doi:10.5589/m08-020
[26] F. Rembold and F. Maselli, “Estimating Inter-Annual
Crop Area Variation Using Multi-Resolution Satellite
Sensor Images,” International Journal of Remote Sensing,
Vol. 25, 2004, pp. 2641-2647.
doi:10.1080/01431160310001657614
[27] F. Rembold and F. Maselli, “Estimation of Inter-Annual
Crop Area Variation by the Application of Spectral Angle
Mapping to Low Resolution Multitemporal NDVI Im-
ages,” Photogrammetric Engineering and Remote Sens-
ing, Vol. 72, No. 1, 2006, pp. 55-62.
[28] Z. Li and J. M. Fox, “Integrating Mahalanobis Typicali-
ties with a Neural Network for Rubber Distribution Map-
ping,” Remote Sensing Letters, Vol. 2, No. 2, 2011, pp.
157-166. doi:10.1080/01431161.2010.505589
[29] P. S. Chavez, “Image-Based Atmospheric Corrections:
Revisited and Improved,” Photogrammetric Engineering
and Remote Sensing, Vol. 62, No. 9, 1996, pp. 1025-
1036.
[30] C. Song, C. E. Woodcock, K. C. Seto, M. Pax-Lenney
and S. A. Macomber, “Classification and Change Detec-
tion Using Landsat TM Data: When and How to Correct
Atmospheric Effects?” Remote Sensing of Environment,
Vol. 75, No. 2, 2001, pp. 230-244.
doi:10.1016/S0034-4257(00)00169-3
[31] M. C. Hansen, D. P. Roy, E. J. Lindquist, B. Adusei, C. O.
Justice and A. Altstatt, “A method for Integrating
MODIS and Landsat Data for Systematic Monitoring of
Forest Cover and Change in the Congo Basin,” Remote
Sensing of Environment, Vol. 112, No. 5, 2008, pp.
2495-2513. doi:10.1016/j.rse.2007.11.012
[32] J. Wang, P. M. Rich, K. P. Price and W. D. Kettle, “Rela-
tions between NDVI and Tree Productivity in the Central
Great Plains,” International Journal of Remote Sensing,
Vol. 25, No. 16, 2004, pp. 3127-3138.
doi:10.1080/0143116032000160499
[33] Y. Yamamoto, T. Oberthür and R. Lefroy, “Spatial Iden-
tifycation by Satellite Imagery of the Crop-Fallow Rota-
tion Cycle in Northern Laos,” Environment, Development
and Sustainability, Vol. 11, No. 3, 2009, pp. 639-654.
doi:10.1007/s10668-007-9134-z
[34] E. P. Crist, “ATM Tasselled Cap Equivalent Transforma-
tion for Reflectance Factor Data,” Remote Sensing of En-
vironment, Vol. 17, No. 3, 1985, pp. 301-306.
doi:10.1016/0034-4257(85)90102-6
[35] T. Han, M. A. Wulder, J. C. White, N. C. Coops, M. F.
Alvarez and C. Butson, “An Efficient Protocol to Process
Landsat Images for Change Detection With Tasselled
Cap Transformation,” IEEE Geoscience and Remote
Sensing Letters, Vol. 4, No. 1, 2007, pp. 147-151.
doi:10.1109/LGRS.2006.887066
[36] C. Huang, B. Wylie, L. Yang, H. Collin and G. Zylstra,
“Derivation of a Tasseled Cap Transformation Based on
Landsat 7 at-Satellite Reflectance,” (Raytheon ITSS, USGS
EROS Data Center, Sioux Falls, SD 57198, USA).
http://landcover.usgs.gov/pdf/tasseled.pdf.
[37] J. M. B. Carreiras, J. M. C. Pereira and J. S. Pereira,
“Estimation of tree Canopy Cover in Evergreen Oak
Woodlands Using Remote Sensing,” Forest Ecology and
Management, Vol. 223, No. 1-3, 2006, pp. 45-53.
doi:10.1016/j.foreco.2005.10.056
[38] G. M. Foody, N. A. Campbell, N. M. Trodd and T. F.
Wood, “Derivation and Applications of Probabilistic
Measures of Class Membership from the Maximum Like-
lihood Classification,” Photogrammetric Engineering and
Remote Sensing, Vol. 58, No. 9, 1992, pp. 1335-1341.
[39] J. R. Eastman, J. Toledano, S. Crema, H. Zhu and H.
Jiang, “In-Process Classification Assessment of Remotely
Sensed Imagery,” GeoCarto International, Vol. 20, No. 4,
2005, pp. 33-44. doi:10.1080/10106040508542362
[40] G. M. Foody, “Hard and Soft Classifications by a Neural
Network with a Non-Exhaustively Defined Set of
Classes,” International Journal of Remote Sensing, Vol.
23, No. 18, 2002, pp. 3853-3864.
doi:10.1080/01431160110109570
[41] J. R. Eastman, “IDRISI: The Taiga Edition,” Clark Labs,
Clark University, Worcester, 2009.