Applied Mathematics, 2011, 2, 1346-1355
doi:10.4236/am.2011.211188 Published Online November 2011 (http://www.SciRP.org/journal/am)
Fuzzy Fault Tree Analysis for Fault Diagnosis of Cannula
Fault in Power Transformer
Sanjay Kumar Tyagi1, Diwakar Pandey2, Vinesh Kumar2
1Department of Applied Mathematics, Amity Institute of Applied Sciences,
Amity University, Noida, India
2Department of Mat hem at i cs, Chaudhary Chara n Singh Universit y, Meerut, India
Received April 17, 2011; revised July 12, 2011; accepted July 19, 2011
Abstract
Being one of the most expensive components of an electrical power plant, the failures of a power transformer
can result in serious power system issues. So fault diagnosis for power transformer is highly important to
ensure an uninterrupted power supply. Due to information transmission mistakes as well as arisen errors
while processing data in surveying and monitoring state information of transformer, uncertain and incom-
plete information may be produced. Based on these points, this paper presents an intelligent fault diagnosis
method of power transformer using fuzzy fault tree analysis (FTA) and beta distribution for failure possibil-
ity estimation. By using the technique we proposed herein, the continuous attribute values are transformed
into the fuzzy numbers to give a realistic estimate of failure possibility of a basic event in FTA. Further, it
explains a new approach based on Euclidean distance between fuzzy numbers, to rank the basic events in
accordance with their Fuzzy Importance Index.
Keywords: Fault Tree, Power Transformer, Fuzzy Sets, Expert Systems, Fuzzy Importance Index
1. Introduction
The involvement of a very larg e number of variables and
their multiple interrelations make the design of a power
transformer very complicated. This complicacy in design
of a power system and variation in operating conditions
causes the occurrence of a fault to be uncertain and ran-
dom. In present paper we introduce a new approach to
the fault detection and analysis of a power transformer.
Fault tree analysis (FTA) is proved to be a very effec-
tive tool to predict probability of hazard caused by a se-
quence and combinations of faults and failure events. A
fault tree is a pictorial representation of various combi-
nations of faults leading to hazard. In fault tree analysis,
we first explore a hazard and then look for events caus-
ing this hazard. In conventional FTA the basic events are
assigned a crisp number. But there are various crucial
and complex systems of great importance, which imparts
vague characteristics. Due to the complexity of systems
and their vague nature, it is very difficult to obtain an
adequate inference about the failure of these systems.
In 1965, L. A. Zadeh [1] suggested a paradigm shift
from a theory of total denial and affirmation to a theory
of grading to give the concept of fuzzy set. H. Tanaka, L.
T. Fan, F. S. Lai and K. Toguchi [2] used fuzzy set the-
ory to replace a crisp number by fuzzy number for better
estimation of failure possibility of top even t. D. Singer [3]
presented fuzzy set theoretic approach to fault tree ana-
lysis. S. Chen [4] used arithmetic of fuzzy numbers to
evaluate system reliability. Zong-Xiao Yang, Kazuhiko
Suzuki, Yukiyasu Shimada and Hayatoshi Sayama [5]
constructed a fuzzy fault diagnostic system, which uses
the fuzzy fault tree analysis to represent knowledge of
the causal relationships in process operation and control
system. Method proposed by him is applied successfully
to a nitric acid cooler process plant. Fuzzy set theoretic
approach for estimating failure rate parameters devel-
oped by D. Pandey and Sanjay Kumar Tyagi [6] provides
comprehensive results in estimation of variety of pa-
rameters involving human judgment, unreported times,
vague operating conditions, etc. D. Pandey and Sanjay
Kumar Tyagi [7] developed a technique that has proven
successful in other areas of knowledge, fuzzy reasoning,
in the evaluation and assessment of equipment failure
modes. In this paper probabilistic consideration of basic
events is replaced with possibilities, thereby leading to

S. K. TYAGI ET AL.1347
fuzzy fault tree analysis.
The failure of power may interrupt various important
operations and make a huge damage to the economy of
any nation. Power transformer is one of the important
electricity equipment used in power networks. Thus the
fault diagnosis and its maintenance in a power transfor-
mer is the utmost priority of power supply enterprises.
Fu Ying-Shun, Liu Fa-Zhan, Zhang Wei-Zheng, Zhang
Quing and Zhang Gui-Xin [8] used rough set theory to
diagnose faults in a power transformer. Chen Yuliang
and Zhang Tiejun [9] also investigated the fuzzy fault
tree method in the machinery equipment fault diagnosis.
In his theory they used fuzzy mathematics to deal with
the uncertainty incurred in the failure pro bability of basic
events. Tong Wu, Guangyu Tu, Z. Q. Bo and A. Klimek
[10] also introduced a method of fault diagnosis of power
transformer. In their work, they used the analysis method
to process the probability of faults withou t statistical data
and developed the methods for the different mode pro-
bability data conversion to triangle fuzzy numbers.
Accurate failure statistics is crucial requirement for re-
liability estimation in power transformer failure. In a si-
tuation, wherein failure data may not be corrected accu-
rately due to various reasons, it is more practical to em-
ploy linguistic terms to express d ata valu e for failure of a
particular event. Since a power transformer may be in-
stalled under different operating conditions. It seems to
be impractical to assign a single fuzzy number to the fai-
lure possibility of the basic events in a fault tree analysis.
To overcome this problem, in present paper we have
categorized the operating condition of a power trans-
former as “Worst Case Condition”, “Condu cive Environ-
ment” and “Highly Conducive Environment” for a power
transformer to work. By “Worst Case Condition” we mean
a situation that rarely occurs i.e. in a state of emergency.
“Conducive Environment” is a normal state where most
of the transformers are installed. Highly Conducive en-
vironment is a very special and conducive environment
created artificially to keep transformer cool and working
for a very long time. Using statistics of failure of power
transformer working under different operating conditions
each basic event is assigned three fuzzy numbers by Ex-
perts A, B and C. But a single fuzzy number is needed
for each basic event to evaluate the failure possibility of
top event. Sanjay Kumar Tyagi, D. Pandey and Reena
Tyagi [11] developed a technique to get a single fuzzy
number for each basic event by taking a fuzzy number
having least variance with all fuzzy number. But in a
natural way, most of the transformers are installed at the
places having “Conducive Environmental Conditions”.
So it is impractical to give equal weightage to the fuzzy
numbers assigned by Expert A, B and C to each basic
event, which may result in the underestimation/over-
estimation of failure possibility of the basic events.
Beta distribution is widely used to model probability
distributions of variables or project parameters in many
areas of operations research like risk analysis for strate-
gic planning, finance and marketing and in decision ana-
lysis [12]. Based on beta distribution, here we proposed a
very precise and pragmatic approach to estimate the fail-
ure possibility of each basic event in fault tree analysis.
Three estimates w, c and h suggested by three
experts A, B and C are taken into consideratio n. It is ob-
served that the median (a crisp number) of the triangular
fuzzy numbers assigned to three estimates w, c and
h are statistically independent. And, since beta distri-
bution is extremely versatile to model variety of uncer-
tainties. So, it is quite usefu l to apply beta distribution to
estimate the parameter “failur e possibility” of basic events.
In our analysis, we generalize this parameter estimation
method by replacing the crisp numbers with fuzzy num-
bers to obtain the failure possib ility of basic events. So it
will enable us to give more realistic estimates for failure
possibility of basic events.
p p p 
p
p 
p

In FTA the basic events have different importance and
improving failure possibility of a basic event having
highest importance will improve the reliab ility of system.
H. Furuta and N. Shiraishi [13] proposed the concept of
fuzzy importance using max-min fuzzy operator and
fuzzy integral. Monte-Carlo simulation is generally used
in the determination of importance measure, even though
computing process is time consuming. Thus for a very
complex system having large number of components, the
whole procedure has to be repeated again and again, thus
not suitable for the fuzzy approach. P. V. Suresh, A. K.
Baber and V. Venkat Raj [14] proposed another method
to evaluate an importance measure called fuzzy impor-
tance measure (FIM). For effective evaluation of the im-
portance index of each basic events, we have introduced
a comparatively easier method to calculate fuzzy impor-
tance index (FII), based Euclidean distance between two
fuzzy numbers. The FII of different basic events leading
Cannula Fault are obtained from the proposed method.
2. Triangular Fuzzy Numbers and Their
Arithmetic
(a) Triangular Fuzzy Number: A fuzzy number
A
 is
termed as triangular fuzzy number if the membership
function of fuzzy number A is shown as follows
112
21
32
32
if
() if
0otherwise
A
xa axa
aa
ax
3
x
axa
aa













 (1)

S. K. TYAGI ET AL. 1348
In our study, we will use a triplet () to denote
a triangular fuzzy number. 123
,,aaa
(b) Operations on triangular fuzzy numbers: The
addition of triangular fu zzy number 123 (, , )
A
aaa
 and
is defined as:
123
(, , )Bbbb


112 23 3
,,

A
Bababab 
 (2)
Thus the addition of two triangular fuzzy numbers is
again a triangular fuzzy number.
Similarly subtraction of two triangular fuzzy numbers
is also a triangular fuzzy number and it can be given by
the following expression:

132231
,,

A
Bababab
 (3)
The multiplication of two fuzzy numbers 123 (, , )
A
aaa

and denoted as A*B can be defi ne d as:
123
(, , )Bbbb

1/2
2
11 1
1/2
2
12 1
()
()( )
0
AB
DDxPTPxQ
o
therwise
x
DDxRU QxR 


 



 




 (4)
where

12121
Taabb 

12121
Uaabb
 
2121 221
Taaabbb
 
, ,
,



2321 32
Ubaaabb
1
,
2
11
2
T
DT , 2
21
2
U
DU  , , ,
11
Pab22 Qab3 Ra
3
b

.
It is evident that the resulting fuzzy number *
A
B
 is
not a triangular fuzzy number. But in most of the cases,
computation with resulting fuzzy numbers becomes very
tedious. Thus it is necessary to avoid the second and
higher degree terms to make them computationally easy
and therefore the product of two fuzzy numbers is re-
duced to a triangular fuzzy number (P, Q, R) or (a1b1,
a2b2, a3b3).
3. Basics of Possibility Theory
Using fuzzy set theory, L. A. Zadeh [15] formulated pos-
sibility theory in term of fuzzy set. This was an attempt
to give a mathematical representation of linguistic un-
certainty, i.e. the uncertainty associated with imprecise
and vague information. In contrast to the objective char-
acter of the probability theory, the possibility theory pro-
vides tools for the modeling of subjective probabilities
[16]. It is based upon the concept of the possibility dis-
tribution. There is a direct connection between possibil-
ity and fuzzy sets. This connection can be explained as
follows:
Let X deno te a variable, taking values from a un iversal
set R and let us consider the equation
X
x, where
x
R be used to describe the fact that the value of X
is x.
Now, we consider a fuzzy set F on R that expresses an
elastic constraint on values to be assigned to X. Then f or
a particular value
x
R

, F(x) gives the degree of com-
patibility of x with the concept described by F. Also for a
given proposition X is F based upon fuzzy set F, it will
be more realistic to interpret F(x) as the degree of possi-
bility that
X
x

. So for a given fuzzy set F on R and
the proposition “X is F” the possibility of
()
F
rx
X
x

for each
x
R

is numerically equal to the de-
gree F(x) to which x belongs to F i.e.
() ()
F
rx Fx

for all
x
R.
The function defined by the equation
given above is clearly a possibility distribution function
on R. For a givenF, the associated possibility measure
(PosF) is defined fo r all
:[0,
F
rX
r
1]
()
A
PX

by the equation
() sup ()
FF
xA
PosAr x


.
4. Fuzzy Operators
Now using algebraic operations on fuzzy numbers (tri-
angular or trapezoidal), we can obtain fuzzy operators
corresponding to Boolean operators “AND”, “OR” etc.
Let 1 2n are the possibility functions of the
basic events i = . Then fuzzy “AND” and
“OR” operators denoted by ANF and ORF respectively,
can be defined a s:
,p
pp 

1, 2,, n
12 1
(, ,, )n
yn
i
pANFpp pp




i

where  denotes the fuzzy multiplication.
Now let ’s are represented by triangular fuzzy
numbers i.e. i
p 
123
(,, )
iiii
paaa

, where i = 1, 2,,n.
Then
121 2 3
11 1
123
(, ,,),,
(, , ),say
nn n
ynii
ii i
yyy
pANFpppa aa
aaa
 







i
3i
a
(5)

12
123
11
12
11 1
123
(, ,,)
111 1(,,)
1(1),1(1),1(1)
(, , ),say.
yn
nn
iiii
ii
nn n
ii
ii i
yyyy
pORFpp p
paaa
aa
paaa

 

 

   





 


(6)
5. Proposed Algorithm to Evaluate Failure
Possibility of Bas ic Events
In this proposed algorithm, fuzzy numbers are used in-
stead of crisp numbers to represent failure probability of

S. K. TYAGI ET AL.1349
occurrence of each basic event in fault tree analysis. For
the sake of simplicity, triangular fuzzy numbers are used
to define the failure possibilit y of the basic events. Also a
triangular fuzzy number is capable to capture the impre-
cision of experts’ assessments, the vagueness of unreli-
able data and easy to compute.
Step 1: First identify an undesirable top event (Haz-
ard), intermediate events and the basic events leading to
top event by exploring history concerned with the failure
of that event. And connect these events using logical
gates “AND” and “OR” to find the pictorial representa-
tion of occurrence of top event.
Step 2: We observe that the basic events are follow-
ing different statistical property of sampled data collec-
ted for a particular event. So the data for the occurrence
of the basic events are collected by three experts A, B
and C taking observations under prescribed conditions
classified as “Worst Case Condition”, “Conducive Envi-
ronment and “Highly Conducive Environment” respec-
tively.
Step 3: Using sampled data collected by the experts A,
B and C the possibility of occurren ce of basic events are
assigned dif ferent fuzzy numbers.
Step 4: It is a well known fact that mostly a system is
operated under “Conducive Environment”. So it is as-
sumed that the data collected for the failure of a basic
event follows a skewed Beta distribution. Thus a tech-
nique based on beta distribution is used to find a single
fuzzy number to the failure possibility of a basic event. If
, and are fuzzy numbers as-
signed to a basic event i by Expert A, B and C taking
observations in “Worst Case Condition”, “Conducive
Environment” and “Highly Conducive Environment” re-
spectively. Then the failu re possibility of the b asic event
may be given as
()
wi
pE

i
E
()
ci
pE
()
hi
pE

E
()4pE () ()
() 6
wici hi
i
pE pE
pE  
. (7)
Step 5: The fuzzy number thus obtained for different
basic events are used to compute failure possibility of top
event.
6. Fuzzy Importance Index (FII)
In fault tree analysis, ranking of basic events as per their
importance play a vital role. To improve reliability of a
system, it is better to improve the reliability of a basic
event, having greater importance instead of the events
with less importance. Let T be the failure possibility
of top event and i
T denote the failure possibility of
occurrence of top event, if the basic event i does not
happen. In other words we can say i
T be the failure
possibility of top event, when failure possibility of basic
event is a crisp number (0 0 0). The distance of
from will determine the importan ce of a basic event
.
p

p

E
p 
i
ET p

i
T
p

i
EA basic event i will be of greater importance than
the other basic event
E
j
E, if the distance between T
and i
T is greater than that of T and p

p
p

j
T. The dis-
tance between two fuzzy numbers may be obtained by
using Hamming or Euclidean distance. The fuzzy impor-
tance of each basic event may be quantified as Fuzzy
Importance I nd e x (FII).
p

FII( ) = Distance of from
i
ET p
i
T
p

If the failure possibilities of the basic events are trian-
gular fuzzy numbers, then the failure possibility of top
event will also be a triangular fuzzy numbers. Here we
denote and i
T by the triplets and
respectively. Thus the FII() for a basic
event may be defined as follows.
T
p

,
iii
u
i
E
p
(,, )lmu
i
E(, )lm
222
II( )ED(,)
()()( )
i
iTT
iii
Epp
llmmuu

 

F (8)
Thus for basic events Ei and Ej, if
then the precipitation of basic event iwill be more
sensitive than that of event
FII( )FII()
ij
EE
E
j
E to improve system reli-
ability. Using this method we can rank the basic events
in accordance with their importance index. And improve
the reliability of the system by prev enting the failure of a
component of greater importance.
7. Case Study: Failure Possibility of
Cannula Fault in Power Transformer
7.1. Fault Tree Analysis of Cannula Fault
The fault tree of Cannula Fault in power transformer is
taken as an analytical example to explain the proposed
algorithm of fault diagnosis process. The fault tree of
Cannula fault in power transformer is shown in Figure 1.
Codes’ meaning of basic and intermediate events of
Cannula Fault are as follows:
Top event T: Cannula Fault;
Intermediate Events:
1
M
: Cannula Overheating;
2
M
: Inside Discharging;
3
M
: Outer Insulated Flashover;
4
M
: Deterioration of Insulation;
5
M
: High Contact Resistance;
6
M
: Abnormal Overvoltage.
Basic Events:
1
E
E: Over loading ;
2
E: Natural Aging;
3
E: Insulated Damping;
4
E: Connector Loosening;
5: Interface Oxygenating;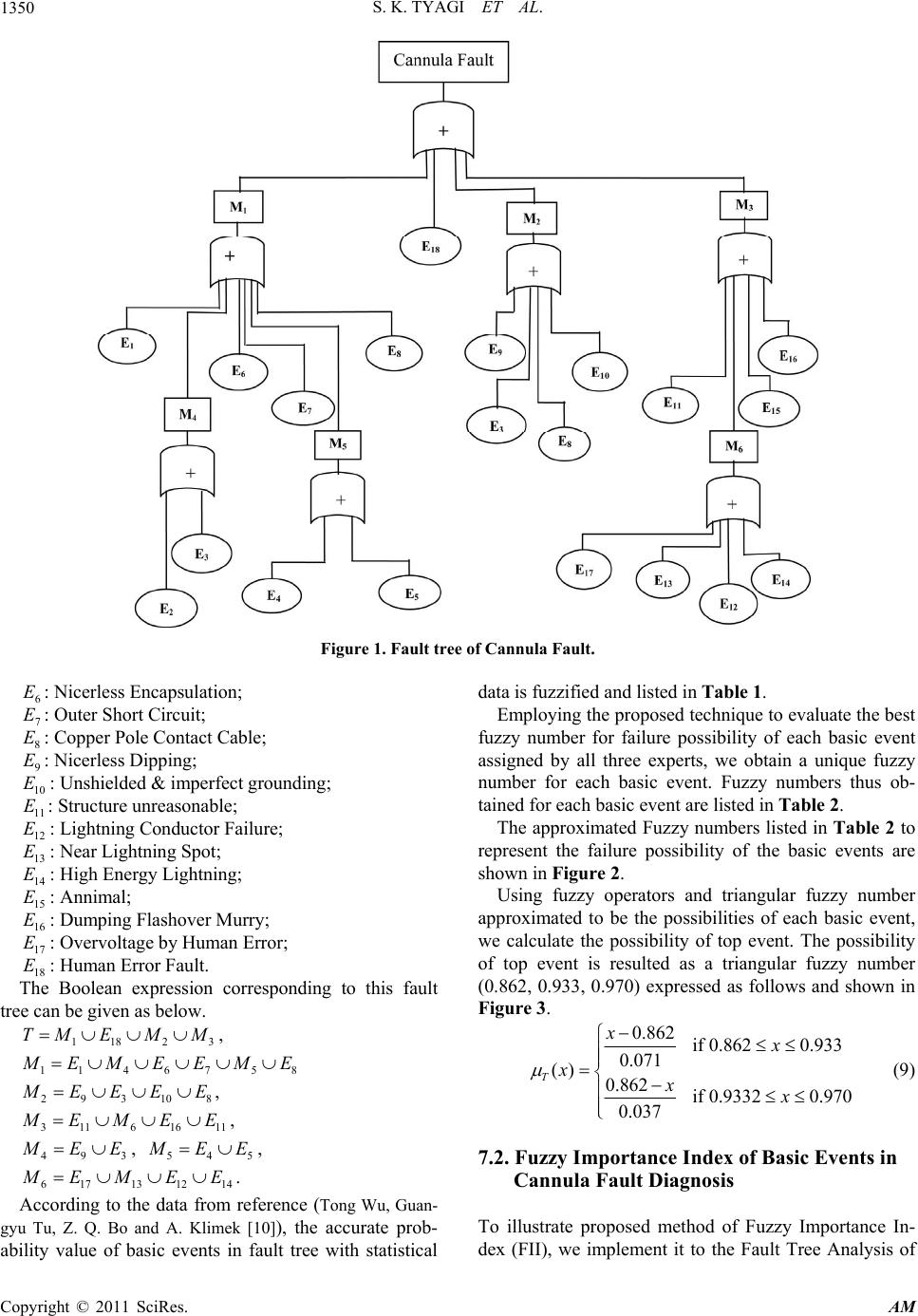

S. K. TYAGI ET AL. 1350
Figure 1. Fault tree of Cannula Fault.
6
E
E: Nicerless Encapsulation;
7
E: Outer Short Circuit;
8
E: Copper Pole Contact Cable;
9
E: Nicerless Dipping;
10
E: Unshielded & imperfect grounding;
11
E: Structure unreasonable;
12
E: Lightning Conductor Failure;
13
E: Near Lightning Spot;
14
E: High Energy Lightning;
15
E: Annimal;
16
E: Dumping Flashover Murry;
17
E: Overvoltage by Human Error;
18
The Boolean expression corresponding to this fault
tree can be given as below.
: Human Error Fault.
118 2
TM EMM
3
8
,
1146 75
M
EM EEME 
293108
M
EEE E ,
3116 16 11
M
EMEE,
493
M
EE, 545
M
EE,
617 131214
M
EMEE .
According to the data from reference (Tong Wu, Guan-
gyu Tu, Z. Q. Bo and A. Klimek [10]), the accurate prob-
ability value of basic events in fault tree with statistical
data is fuzzified and listed in Table 1.
Employing the propo sed technique to evaluate th e best
fuzzy number for failure possibility of each basic event
assigned by all three experts, we obtain a unique fuzzy
number for each basic event. Fuzzy numbers thus ob-
tained for each basic event are listed in Table 2.
The approximated Fuzzy numbers listed in Table 2 to
represent the failure possibility of the basic events are
shown in Figure 2.
Using fuzzy operators and triangular fuzzy number
approximated to be the possibilities of each basic event,
we calculate the possibility of top event. The possibility
of top event is resulted as a triangular fuzzy number
(0.862, 0.933, 0.970) expressed as follows and shown in
Figure 3. 0.862 if0.8620.933
0.071
() 0.862 if 0.93320.970
0.037
T
xx
xxx 








(9)
7.2. Fuzzy Importance Index of Basic Events in
Cannula Fault Diagnosis
To illustrate proposed method of Fuzzy Importance In-
dex (FII), we implement it to the Fault Tree Analysis of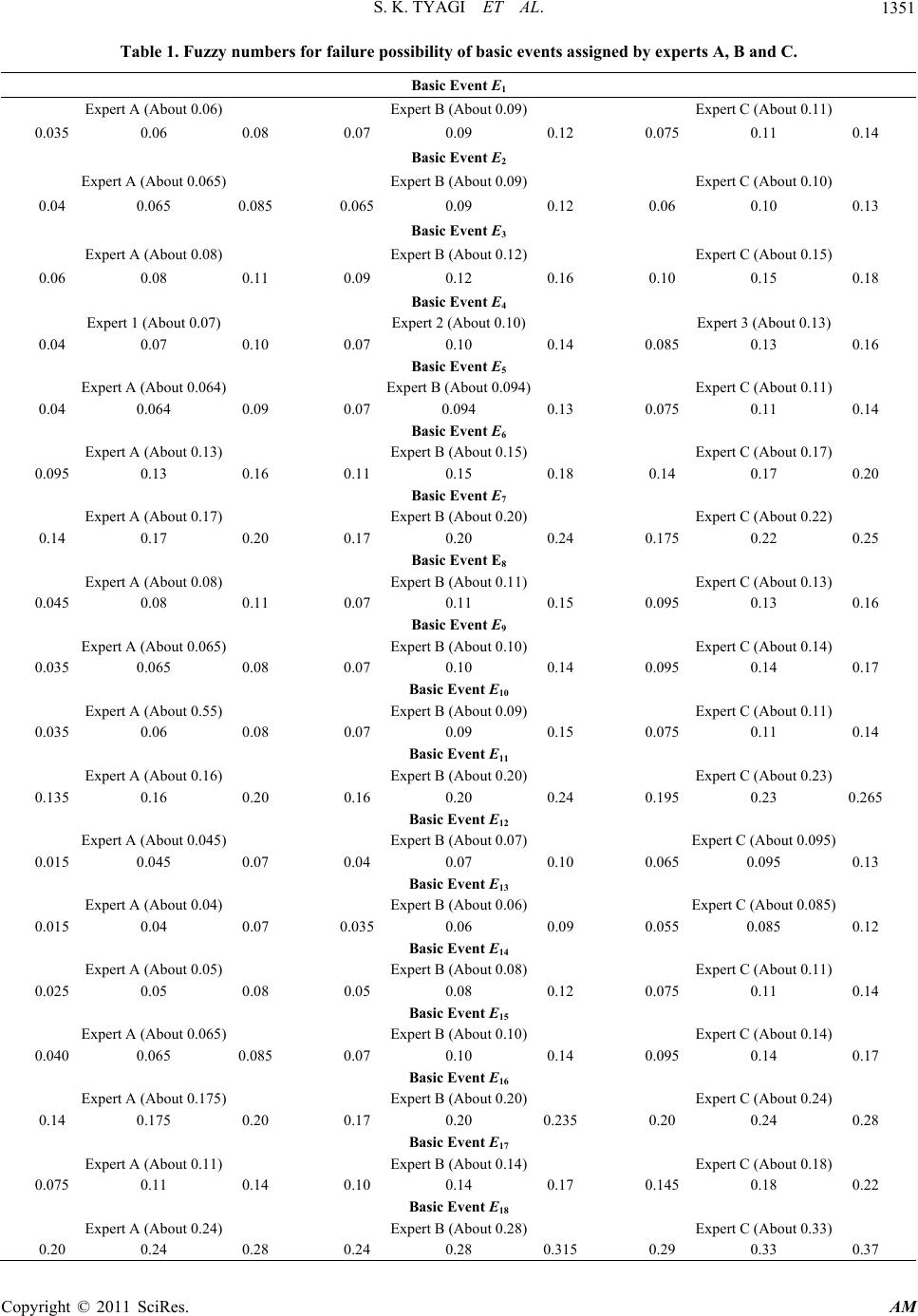

S. K. TYAGI ET AL. 1351
Table 1. Fuzzy numbers for failure possibility of basic events assigned by experts A, B and C.
Basic Event E1
Expert A (About 0.06) Expert B (About 0.09) Expert C (About 0.11)
0.035 0.06 0.08 0.07 0.09 0.12 0.075 0.11 0.14
Basic Event E2
Expert A (About 0.065) Expert B (About 0.09) Expert C (About 0.10)
0.04 0.065 0.085 0.065 0.09 0.12 0.06 0.10 0.13
Basic Event E3
Expert A (About 0.08) Expert B (About 0.12) Expert C (About 0.15)
0.06 0.08 0.11 0.09 0.12 0.16 0.10 0.15 0.18
Basic Event E4
Expert 1 (About 0.07) Expert 2 (About 0.10) Expert 3 (About 0.13)
0.04 0.07 0.10 0.07 0.10 0.14 0.085 0.13 0.16
Basic Event E5
Expert A (About 0.064) Expert B (About 0.094) Expert C (About 0.11)
0.04 0.064 0.09 0.07 0.094 0.13 0.075 0.11 0.14
Basic Event E6
Expert A (About 0.13) Expert B (About 0.15) Expert C (About 0.17)
0.095 0.13 0.16 0.11 0.15 0.18 0.14 0.17 0.20
Basic Event E7
Expert A (About 0.17) Expert B (About 0.20) Expert C (About 0.22)
0.14 0.17 0.20 0.17 0.20 0.24 0.175 0.22 0.25
Basic Event E8
Expert A (About 0.08) Expert B (About 0.11) Expert C (About 0.13)
0.045 0.08 0.11 0.07 0.11 0.15 0.095 0.13 0.16
Basic Event E9
Expert A (About 0.065) Expert B (About 0.10) Expert C (About 0.14)
0.035 0.065 0.08 0.07 0.10 0.14 0.095 0.14 0.17
Basic Event E10
Expert A (About 0.55) Expert B (About 0.09) Expert C (About 0.11)
0.035 0.06 0.08 0.07 0.09 0.15 0.075 0.11 0.14
Basic Event E11
Expert A (About 0.16) Expert B (About 0.20) Expert C (About 0.23)
0.135 0.16 0.20 0.16 0.20 0.24 0.195 0.23 0.265
Basic Event E12
Expert A (About 0.045) Expert B (About 0.07) Expert C (About 0.095)
0.015 0.045 0.07 0.04 0.07 0.10 0.065 0.095 0.13
Basic Event E13
Expert A (About 0.04) Expert B (About 0.06) Expert C (About 0.085)
0.015 0.04 0.07 0.035 0.06 0.09 0.055 0.085 0.12
Basic Event E14
Expert A (About 0.05) Expert B (About 0.08) Expert C (About 0.11)
0.025 0.05 0.08 0.05 0.08 0.12 0.075 0.11 0.14
Basic Event E15
Expert A (About 0.065) Expert B (About 0.10) Expert C (About 0.14)
0.040 0.065 0.085 0.07 0.10 0.14 0.095 0.14 0.17
Basic Event E16
Expert A (About 0.175) Expert B (About 0.20) Expert C (About 0.24)
0.14 0.175 0.20 0.17 0.20 0.235 0.20 0.24 0.28
Basic Event E17
Expert A (About 0.11) Expert B (About 0.14) Expert C (About 0.18)
0.075 0.11 0.14 0.10 0.14 0.17 0.145 0.18 0.22
Basic Event E18
Expert A (About 0.24) Expert B (About 0.28) Expert C (About 0.33)
0.20 0.24 0.28 0.24 0.28 0.315 0.29 0.33 0.37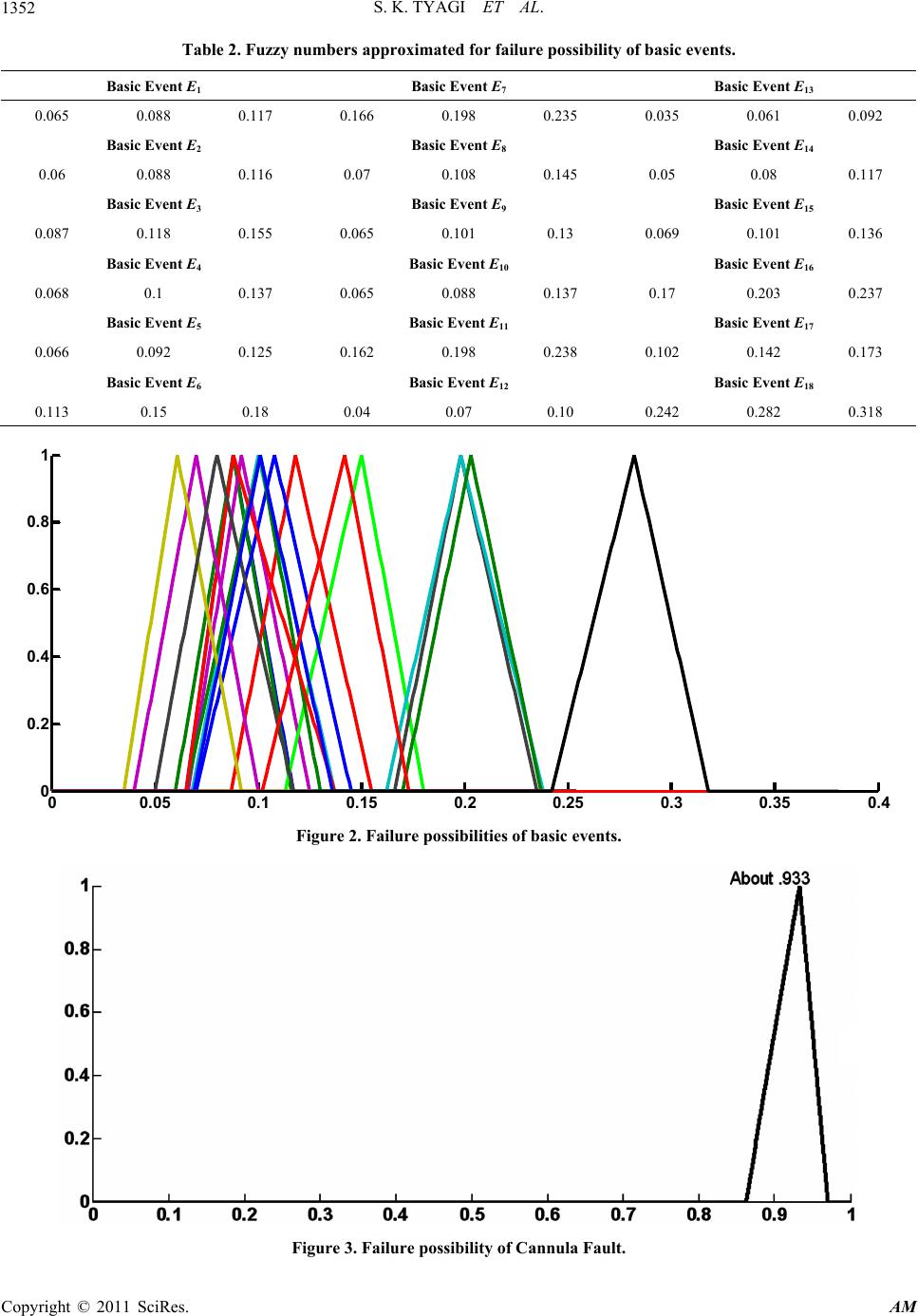

S. K. TYAGI ET AL. 1352
Table 2. Fuzzy numbers approximated for failure possibility of basic events.
Basic Event E1 Basic Event E7 Basic Event E13
0.065 0.088 0.117 0.166 0.198 0.235 0.035 0.061 0.092
Basic Event E2 Basic Event E8 Basic Event E14
0.06 0.088 0.116 0.07 0.108 0.145 0.05 0.08 0.117
Basic Event E3 Basic Event E9 Basic Event E15
0.087 0.118 0.155 0.065 0.101 0.13 0.069 0.101 0.136
Basic Event E4 Basic Event E10 Basic Event E16
0.068 0.1 0.137 0.065 0.088 0.137 0.17 0.203 0.237
Basic Event E5 Basic Event E11 Basic Event E17
0.066 0.092 0.125 0.162 0.198 0.238 0.102 0.142 0.173
Basic Event E6 Basic Event E12 Basic Event E18
0.113 0.15 0.18 0.04 0.07 0.10 0.242 0.282 0.318
00.050.1 0.150.2 0.250.3 0.350.4
0
0. 2
0. 4
0. 6
0. 8
1
Figure 2. Failure possibilities of basic events.
Figure 3. Failure possibility of Cannula Fault.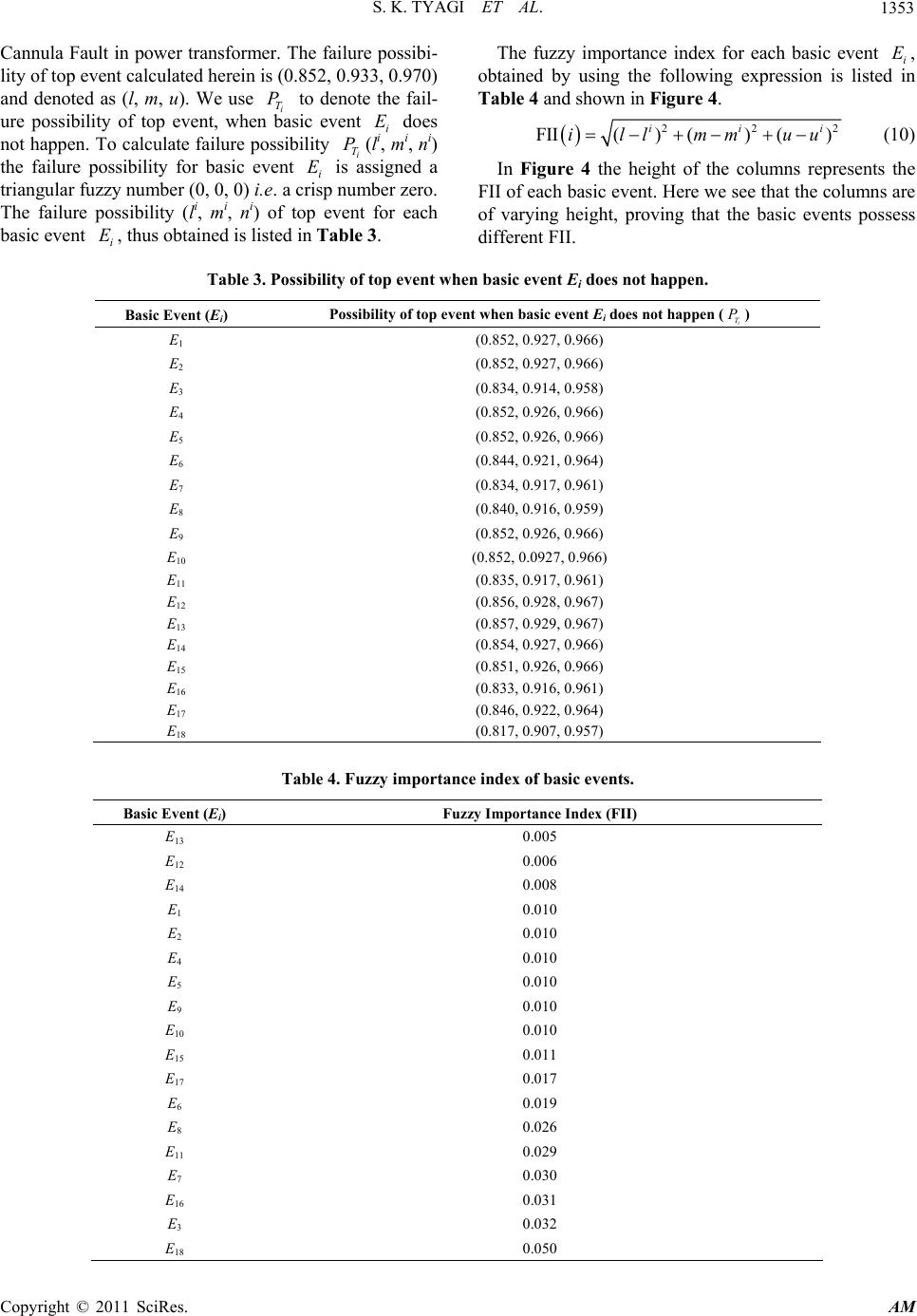

S. K. TYAGI ET AL. 1353
The fuzzy importance index for each basic event i,
obtained by using the following expression is listed in
Table 4 and shown in Figure 4.
ECannula Fault in power transformer. The failure possibi-
lity of top event calculated herein is (0.852, 0.933, 0.970)
and denoted as (l, m, u). We use i
T to denote the fail-
ure possibility of top event, when basic event i does
not happen. To calculate failure possibility i
T(li, mi, ni)
the failure possibility for basic event i is assigned a
triangular fuzzy number (0, 0, 0) i.e. a crisp number zero.
The failure possibility (li, m
i, ni) of top event for each
basic event , thus obtained is listed in Table 3.
PE
P
E
i
E

22
FII()()()
ii
illmmuu
2i
(10)
In Figure 4 the height of the columns represents the
FII of each basic event. Here we see that the columns are
of varying height, proving that the basic events possess
different FII.
Table 3. Possibility of top event when basic event Ei does not happen.
Basic Event (Ei) Possibility of top event when basic event Ei does not happen ()
i
T
P
E1 (0.852, 0.927, 0.966)
E2 (0.852, 0.927, 0.966)
E3 (0.834, 0.914, 0.958)
E4 (0.852, 0.926, 0.966)
E5 (0.852, 0.926, 0.966)
E6 (0.844, 0.921, 0.964)
E7 (0.834, 0.917, 0.961)
E8 (0.840, 0.916, 0.959)
E9 (0.852, 0.926, 0.966)
E10 (0.852, 0.0927, 0.966)
E11 (0.835, 0.917, 0.961)
E12 (0.856, 0.928, 0.967)
E13 (0.857, 0.929, 0.967)
E14 (0.854, 0.927, 0.966)
E15 (0.851, 0.926, 0.966)
E16 (0.833, 0.916, 0.961)
E17 (0.846, 0.922, 0.964)
E18 (0.817, 0.907, 0.957)
Table 4. Fuzzy importance index of basic events.
Basic Event (Ei) Fuzzy Importance Index (FII)
E13 0.005
E12 0.006
E14 0.008
E1 0.010
E2 0.010
E4 0.010
E5 0.010
E9 0.010
E10 0.010
E15 0.011
E17 0.017
E6 0.019
E8 0.026
E11 0.029
E7 0.030
E16 0.031
E3 0.032
E18 0.050

S. K. TYAGI ET AL. 1354
Figure 4. Fuzzy Importance Index (FII) of basic events.
8. Conclusions and Discussion of Result
In present paper, we introduce a novel approach to ap-
proximate the failure possibility of basic events, if more
than one fuzzy number is assigned to a particular basic
event by different experts. The possibilities of basic
events are considered to be triangular fuzzy numbers.
Three fuzzy numbers are assigned to each basic event by
the Experts A, B and C. These experts collect data of
failure for each component in three different operating
conditions “Worst Case Condition”, “Conducive Envi-
ronment” and “Highly Conducive Environment”. Unlike
previous techniques, we investigate the operating condi-
tions rigorously and assess the weightage of each of them.
Taking view of this, we use the parameter estimation
method used in PERT method and generalize it by re-
placing crisp numbers with fuzzy numbers, to obtain
most likely fuzzy number to represent the failure possi-
bility of basic events. The proposed method seems to be
very pragmatic and preclude underestimation/overesti-
mation of failure possibility for basic events.
Also it is a well known fact that all basic events do not
contribute equally in failure of a system i.e. the occur-
rence of top event. Thus it is important to assess the im-
portance of each basic event. Herein we employ a very
effective and computationally easy technique based on
Euclidean Distance between fuzzy numbers.
The proposed methods are implemented to the Can-
nula Fault in Power Transformer. We have eighteen ba-
sic events leading the occurrence of top event. Using
proposed technique to calculate FII of basic events, we
list them in Table 4 in ascending order of their FII and
put in Figure 4. We conclude that the basic event 18
having highest FII, causes precipitation of system more
rapidly than the basic event 13 with least FII. There-
fore the reliability of Cannula and hence of Power
Transformer may be improved by preventing occurrence
of basic event .
E
E
18
E
9. Acknowledgements
The authors are grateful to the anonymous reviewers for
their critical evaluation and constructive suggestions.
10. References
[1] L. A. Zadeh, “Fuzzy Sets,” Information and Control, Vol.
8, No. 3, 1965, pp. 338-353.
doi:10.1016/S0019-9958(65)90241-X
[2] H. Tanaka, L. T. Fan, F. S. Lai and K. Toguchi, “Fault-
Tree Analysis by Fuzzy Probability,” IEEE Transactions
on Reliability, Vol. 32, No. 5, 1983, pp. 453-457.
doi:10.1109/TR.1983.5221727
[3] D. Singer, “A Fuzzy Set Approach to Fault Tree Analy-
sis,” Fuzzy Sets and Systems, Vol. 34, No. 2, 1990, pp.
145-155. doi:10.1016/0165-0114(90)90154-X
[4] S. Chen, “Fuzzy System Reliability Analysis Using Fu-
zzy Number Arithmetic Operations,” Fuzzy Sets and Sys-
tems, Vol. 64, No. 1, 1994, pp. 31-38.
doi:10.1016/0165-0114(94)90004-3
[5] Z.-X. Yang, K. Suzuki, Y. Shimada and H. Sayama, “Fu-
zzy Fault Diagnostic System Based on Fault Tree Analy-
sis,” Proceedings of the International Joint Conference of
the Fourth IEEE International Conference on Fuzzy Sys-
tems and The Second International Fuzzy Engineering

S. K. TYAGI ET AL.1355
Symposium, Yakohama, 20-24 March 1995, Vol. 1, pp.
165-170. doi:10.1109/FUZZY.1995.409676
[6] D. Pandey and S. K. Tyagi, “Profust Reliability of a
Gracefully Degradable System,” Fuzzy Sets and Systems,
Vol. 158, No. 7, 2007, pp. 794-803.
doi:10.1016/j.fss.2006.10.022
[7] D. Pandey, S. K. Tyagi and V. Kumar, “Failure Mode
Screening Using Fuzzy Set Theory,” International Ma-
thematical Forum, Vol. 4, No. 16, 2009, pp. 779-794
[8] Y.-S. Fu, F.-Z. Liu, W.-Z. Zhang, Q.-I. Zhang and G.-X.
Zhang, “The Fault Diagnosis of Power Transformer Based
on Rough Set Theory,” Proceedings of the China Interna-
tional Conference on Electricity Distribution, Guangzhou,
10-13 December 2008, pp. 1-5.
[9] Y. L. Chen and T. J. Zhang, “Research on Application of
Fuzzy Fault Tree Analysis Method in the Machinery
Equipment Fault Diagnosis,” Proceedings of 2nd Inter-
national Conference on Informatics in Control, Automa-
tion and Robotics, Wuhan, 6-7 March 2010, pp. 84-87.
[10] T. Wu, G. Y. Tu, Z. Q. Bo and A. Klimek “Fuzzy Set
Theory and Fault Tree Analysis Based Method Suitable
for Fault Diagnosis of Power Transformer,” Proceedings
of the 14th International Conference on the Intelligent
System Applications to Power Systems, Kaohsiung, 5-8
November 2007, pp. 487-491.
doi:10.1109/ISAP.2007.4441664
[11] S. K. Tyagi, D. Pandey and R. Tyagi, “Fuzzy Set Theoretic
Approach to Fault Tree Analysis,” International Journal of
Engineering, Science and Technology, Vol. 2, No. 5, 2010,
pp. 276-283.
[12] S. D. Moitra, “Skewness a nd the Beta Distribution,” Jour-
nal of Operational Research Society, Vol. 41, No. 10, 1990,
pp. 953-961.
[13] H. Furuta and N. Shiraishi, “Fuzzy Importance in Fault
Tree Analysis,” Fuzzy Sets and Systems, Vol. 12, No. 3,
1984, pp. 205-213. doi:10.1016/0165-0114(84)90068-X
[14] P. V. Suresh, A. K. Babar and V. V. Raj, “Uncertainty in
Fault Tree Analysis: A Fuzzy Approach,” Fuzzy Sets and
Systems, Vol. 83, No. 2, 1996, pp. 135-141.
doi:10.1016/0165-0114(95)00386-X
[15] L. A. Zadeh “Fuzzy Sets as the Basis for a Theory of Po-
ssibility,” Fuzzy Sets and Systems, Vol. 1, No. 1, 1978, pp.
3-28. doi:10.1016/0165-0114(78)90029-5
[16] G. J. Klir and B. Yuan, “Fuzzy Sets and Fuzzy Logic:
Theory and Applications,” Prentice-Hall, Upper Saddle
River, 1995.