Open Access Library Journal
Vol.05 No.10(2018), Article ID:87785,7 pages
10.4236/oalib.1104788
On Semi π-Regular Local Ring
Zubayda M. Ibraheem, Raghad A. Mustafa, Maha F. Khalf
Department of Mathematics, College of Computer and Mathematical Sciences, University of Mosul, Mosul, Iraq
Copyright © 2018 by authors and Open Access Library Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 21, 2018; Accepted: October 9, 2018; Published: October 12, 2018
ABSTRACT
A ring R is said to be a right (left) semi π-regular local ring if and only if for all a in R, either a or is a right (left) semi π-regular element. The purpose of this paper is to give some characterization and properties of semi π-regular local rings, and to study the relation between semi π-regular local rings and local rings. From the main results of this work: 1) Let R be a semi π-regular reduced ring. Then the idempotent associated element is unique. 2) Let R be a ring. Then R is a right semi π-regular local ring if and only if either or is direct summand for all and . If R is a local ring with for all and , then R is a right semi π-regular local ring.
Subject Areas:
Algebra
Keywords:
Local, Ring, Semi π-Regular

1. Introduction
Throughout this paper, R will be an associative ring with identity. For , , denote the right (left) annihilator of a. A ring R is reduced if R contains, no non-zero nilpotent element.
A ring R is said to be Von Neumann regular (or just regular) if and only if for each a in R, there exists b in R such that [1] . Following [2] , a ring R is said to be right semi-regular if and only if for each a in R, there exists b in R such that and .
By extending the notion of a right semi π-regular ring to a right semi-regular ring is defined as follows:
A ring R is said to be right semi π-regular if and only if for each a in R, there exist positive integers n and b in R such that and [3] .
Following [4] , a ring R is said to be π-regular if and only if for each a in R, there exist positive integers n and b in R such that . A ring R is called a local ring, if it has exactly one maximal ideal [5] .
A ring R is said to be a local semi-regular ring, if for all a in R, either a or is a semi-regular element [6] .
We extend the notion of the local semi-regular ring to the semi π-regular local ring defined as follows:
A ring R is said to be a semi π-regular local ring, if for all a in R, either a or is a semi π-regular element.
Clearly that every π-regular ring is a semi π-regular local ring.
2. A Study of Some Characterization of Semi π-Regular Local Ring
In this section we give the definition of a semi π-regular local ring with some of its characterization and basic properties.
2.1. Definition
A ring R is said to be right (left) semi π-regular local ring if and only if for all a in R, either a or is right (left) semi π-regular element for every a in R.
Examples:
Let be a ring and let is cyclic group, then is π-regular ring. Thus R is semi π-regular local ring.
Let R be the set of all matrix in which is defined as:
.
It easy to show that R is semi π-regular local ring.
2.2. Proposition
Let R be a right semi π-regular local ring. Then the associated elements are idempotents.
Proof:
Let , since R is right semi π-regular local ring. Then either a or is right semi π-regular element, that there exists b in R such that and , so , gives . Thus , which implies . Now, if is right semi π-regular element, then there exists c in R such that and . So , thus . Hence and therefore .
In general the associated element is not unique. But the following proposition give the necessary condition to prove the associated element is unique.
2.3. Proposition
Let R be a right semi π-regular local reduced ring. Then the idempotent associated element is unique.
Proof:
Let , since R is right semi π-regular local ring. Then either a or is right semi π-regular element in R. If a is right semi π-regular element, then there exists such that and . Assume that, there is an element in R such that and , which implies that , hence and , that is and then , , which implies , .
Since R is reduced ring, then . Hence and then and which implies and . Hence and , and therefore . Now, if is right semi π-regular element, then there exists an element such that and . Now, we assume that the associated element c is not unique.
Then, there exists such that , , then which implies that , that is . Hence and , implies that and , that is and . Since R is reduced ring, then and then , , that is and . Thus and . Therefore .
The following theorem give the condition to a semi π-regular local ring to be π-regular ring.
2.4. Theorem
Let R be a right semi π-regular local ring. Then any element is π-regular if for any associated element b in R.
Proof:
Let
and R be a right semi π-regular local ring. Then either
Now, assume that . Then and , . Since b is idempotent element, then and , it follows that .
Thus . Therefore a is π-regular element in R.
Now, if is right semi π-regular element, then there exists an element such that : and .
If , assume that , where , . Since c is idempotent element, then and , it follows that , that is .
Thus . Therefore is π-regular element in R.
2.5. Proposition
The epimorphism image of right semi π-regular local ring is right semi π-regular local ring.
Proof:
Let be epimorphism homomorphism function from the ring π in to the ring , where R is right semi π-regular local ring and let be element s in . Then there exists elements in R such that
.
Now, since R is right semi π-regular local ring, then either x or is right semi π-regular element, that is and . Then
.
Now, to prove . If , then , that is , then , and , hence .
Thus , that is . Then , thus . Hence . Therefore,
(1)
Now, let . Then , it follows that and then .
Thus and hence . Therefore
(2)
from (1) and (2), we obtain .
Now, if is right semi π-regular element in R, then and .
Now, . Thus .
Now, to prove .
Let . Then . That is , then and . Then and hence , that is , it follows that .
Hence , thus . Therefore
(3)
Now, let , implies to , hence , thus . Hence . Therefore
(4)
from (3) and (4) we obtain
, that is either y or 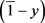 is right semi π-regular element in
is right semi π-regular element in . Therefore
. Therefore 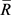 is right semi π-regular local ring.
is right semi π-regular local ring.
2.6. Theorem
Let R be a ring. Then R is right semi π-regular local ring if and only if either 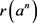 or
or  is direct summand for all
is direct summand for all 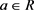 and
and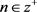 .
.
Proof:
Let 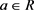 and
and  is direct summand. Then there exists an ideal
is direct summand. Then there exists an ideal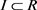 , such that
, such that . Thus, there is
. Thus, there is  and
and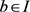 , such that
, such that 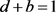 and hence
and hence 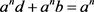 and therefore
and therefore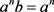 . Now, to prove
. Now, to prove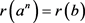 , let
, let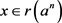 . Then
. Then







and by the same way we can prove

from (5) and (6) we obtain


Then, there exists an ideal 





Therefore

Let

Thus,
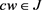




Now, let





form (7) and (8) we obtain

Now, let R be aright semi π-regular local ring. Then either a or 


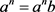

Hence, 




Now, to prove













Now, if 






Hence,

Now, to prove

Then 







Hence 


That is

Now, to give the relation between semi π-regular local ring and local ring.
2.7. Theorem
If R is local ring with 


Proof:
Let R be local ring. Then either a or 
If a is invertible, then there exists an element b in R such that







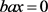



Now, let





from (9) and (10) we obtain













Now, let





form (11) and (12) we have

3. The Conclusion
From the study on characterization and properties of semi π-regular local rings, we obtain the following results:
1) Let R be a right semi π-regular local ring. Then the associated elements are idempotents.
2) Let R be a right semi π-regular local ring. Then the idempotent associated element is unique.
3) Let R be a right semi π-regular local ring. Then any element 

4) The epimorphism image of right semi π-regular local ring is right semi π-regular local ring.
5) Let R be a ring. Then R is a right semi π-regular local ring if and only if either 



If R is a local ring with 


Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Ibraheem, Z.M., Mustafa, R.A. and Khalf, M.F. (2018) On Semi π-Regular Local Ring. Open Access Library Journal, 5: e4788. https://doi.org/10.4236/oalib.1104788
References
- 1. Von Neumann, J. (1936) On Regular Rings. Proceedings of the National Academy of Sciences of the United States of America, 22, 707-713.
https://doi.org/10.1073/pnas.22.12.707 - 2. Shuker, N.H. (1994) On Semi-Regular Ring. Journal of Education and Science, 21, 183-187.
- 3. Al-Kouri, M.R.M. (1996) On π-Regular Rings. M.Sc. Thesis, Mosul University, Mosul.
- 4. Kim, N.K. and Lee, Y. (2011) On Strongly π-Regularity and π-Regularity. Communications in Algebra, 39, 4470-4485.
https://doi.org/10.1080/00927872.2010.524184 - 5. Burton, D.M. (1970) A First Course in Rings and Ideals. Addison Wesley Publishing Company, Boston.
- 6. Abdullah, F.A. (2013) On Local and Local Semi Regular Rings. M.Sc. Thesis, Mosul University, Mosul.


