Engineering, 2009, 1, 196-200
doi:10.4236/eng.2009.13023 Published Online November 2009 (http://www.scirp.org/journal/eng).
Analysis for Transverse Sensitivity of the
Microaccelerometer
Yu LIU1,2,3, Guochao WANG1,2,3, Changwen GUO1,2,3
1Automobile College, Chongqing University of Technology, Chongqing, China
2Key Laboratory of Automobile Parts & Test Technique in Chongqing, Chongqing, China
3Chongqing Engineering Research Center for Automobile Power System and Control, Chongqing, China
Received January 10, 2009; revised February 21, 2009; accepted February 23, 2009
Abstract
For the microaccelerometer, strong axial response and weak cross-axial one are always expected. This paper
presents a general analysis about transverse sensitivity of the microaccelerometer. The analysis model is de-
veloped, where the influence of response stiffness and damping in different axes, as well as symmetrical de-
cline angles of 3 degrees of freedom system is considered. Moreover, multi-freedom vibration equations
based on the analysis model are established. And the equations are solved on condition that damping force is
ignored. Finally, the theoretical analysis about transverse sensitivity is accomplished, and some effective
methods, which are beneficial to reduce cross disturbance, are provided.
Keywords: MEMS, Accelerometers, Transverse Sensitivity, Multi-Freedom Vibration Equation
1. Introduction
For the microaccelerometer, there should be no output if
the input acceleration is along the cross axis. In fact,
however, the output created by forces induced in or-
thogonal axis is not equal to zero. This phenomena is
called cross coupling, which is measured by transverse
sensitivity [1–3].
In this paper, the analysis model for cross disturbance
of the microaccelerometer is developed, where the in-
fluence of response stiffness and damping in different
axes, as well as symmetrical decline angles of 3 degrees
of freedom system is considered. Moreover, multi- free-
dom vibration equations based on the analysis model are
established. And the equations are solved on condition
that damping force is ignored. Finally, the theoretical
analysis about transverse sensitivity is accomplished, and
some effective methods, which are beneficial to reduce
cross disturbance, are provided.
2. Transverse Sensitivity
Transverse sensitivity is the ratio of the output caused by
acceleration perpendicular to the main sensitivity axis
divided by the basic sensitivity in the main direction. It is
an important characteristic of the microaccelerometer,
and is primarily caused by two factors [4–6]. One is from
the inherent microstructure, which may be eliminated by
adopting the appropriate working principle and optimiz-
ing the design parameters. The other is from inaccuracies
in fabrication process, package orientation and mis-
alignment, which is only to be reduced as possible as we
can.
For example, x-axis accelerometer, due to inevitability
of errors in fabrication and misalignments, the applied
acceleration can be expressed as acceleration along the
x-axis and accelerations perpendicular to the main sensi-
tivity axis, denoted as ,,
x
yz
aaa


respectively. Therefore,
the output is given by
zzxyyxxxxout aSaSaSV 


………….(1)
where Syx or Szx is transverse sensitivity of x-axis in y or z
direction. Unfortunately, the accelerometer cannot dis-
tinguish the change in voltage caused by accelerations
y
a

and
z
a

, which results in a difference of Syxay＋Szxaz .
Disturbance and coupling from different axes have
important influences on the performance of the microac-
celerometer. So strong axial response and weak cross-
axial one are always expected. And the transverse sensi-
tivity is always expected to small enough, even close to
zero.

Y. LIU ET AL.197
, the microstructure of the accelerometer can
e represented as a mass-spring-damper system. Figure 1
3. Analysis of Transverse Sensitivity
3.1. Model
In most cases
b
shows the mechanical model of the microaccelerometer
with a single x- degree of freedom. In perfect condition,
elastic deformation of the spring induced by the inertial
force is always along the x-axis no matter where accel-
eration signal is from. In fact, however, the phenomenon
of cross coupling exists inevitably. On the one hand, the
elastic deformation of the equivalent spring occurs not
only in primary x-axis but also in orthogonal y-axis and
z-axis, and on the other hand, the displacement of the
microstructure under acceleration
x
a
 is not always along
the primary x-axis, which may be at an angle with the
ideal sensitive axis [7].
Figure 2 illustrates the mechanical model of microac-
celerometer with three degrees of freedom, where elastic
deformation is along x-axis, y-axis and z-axis. So the
acceleration ponderance ,,
x
yz
aaa

are detected by the
corresponding degree of system. Because the
microstructure has the sa mass, the different
equivalent stiffness and damping coefficients, denoted as
Kx, Ky, Kz and Bx, By, Bz respectively, the model in Figure
2 is the analysis model of cross disturbance resulted from
stiffness and damping in different axes.
freedom
me proof
Figure 1. Simplified mechanical model of the microaccel-
erometer with a single x- degree of freedom.
Figure 2. Analysis model of cross disturbanceesulted from
stiffness and damping in different axes.
are not along the
pr
r
Figure 3 shows the other model of the microacceler-
ometer, where the spring and the damper
imary axis but that at an angle with the corresponding
ideal axis. For example, x- degree of freedom system, as
illustrated in Figure 3(a), due to inevitability of errors in
fabrication process, package orientation as well as mis-
alignment, the spring Kx and damper Bx are all at an angle
with x-axis, which is called symmetrical decline angle
anddenoted as
x

. At the same time, the spring Kx and
damper Bx are also at an angle with y-axis or z-axis, de-
noted as ,
x
x

 respectively. Most often,
x

is quite
small, and ,
x
x

are all close to 2

. Therre,
cos co1
xx

efo
222
coss x 

 (2)
Similarly, ,
yz


are the symmetrical de
y- and gree of freedom syste
shre 3 (b
mmetrical decline angles.
ze the influence of cross disturbance, the
ulti-freedom vibration equations based on the above-
cline angles of
z- dems respectively, as
own in Figu) and (c).
So the model in Figure 3 is the analysis model of cross
disturbance resulted from the sy
3.2. Solution
In order to analy
m
mentioned models should be established.
Here sinusoidal signal is considered. sin
x
at

,
asin
yt

, sin
z
at

denote three projecti-
ation Furthermore, assume the
ntis as follows:
()
()
sin
x
xx
x
wW t
ons of vec
tor accelerrespectively.
displaceme function
()
sin
sin
yy
x
zz
wW t
wW t








(3)
where ()x
x
W,()
x
y
W,()
x
z
W are the amplitudes along the x, y
irection respectiv
-deee fre
al
and z-dely.
For xgrofedom system, the vibration equation
responded to acceleration sign sinat
x

is given by:
si n
xx xx xx xy xzxx
ww mat BBB KK
0
0
xy xz
yxyyyyz yxyyy yzy
xz yz zzxzyzzz
zz z
w K
mw BBBw KKKw
BBB KKK
ww w

 
  


 
  


 

 
 
 


 
 

   
 
 
(4)
where wx, wy, wz are the displacements o
along the x, y and z-direction respectively.
f proof mass
x
w , w
,
y
z
w

and
x
w
 , y
w
 ,
z
w
 denote the first and the seconri
tive ofce wx, wy, wz with respect to time t re-
spect lyxx, y, Kzz are the self-stiffness of equiva-
d deva-
displament
ive. KKy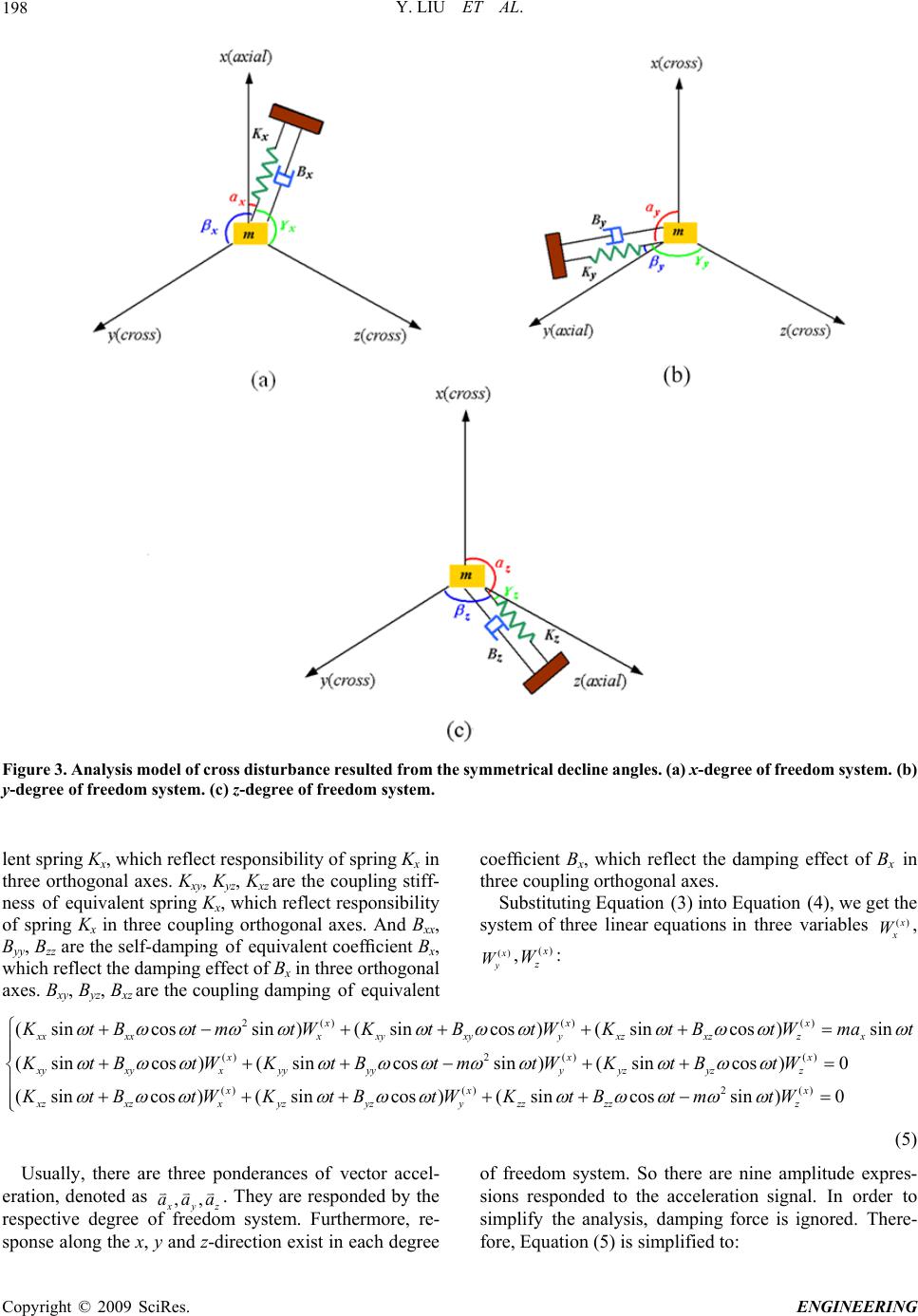

Y. LIU ET AL. 198
Figure 3. Analysis model of cross disturbance resulted from the symmetrical decline angles. (a) x-degree of freedom syem. (b)
lent spring Kx, which reflect responsibility of spring Kx in coefficient Bx, which reflect the damping effect of Bx in
st
y-degree of freedom system. (c) z-degree of freedom system.
three orthogonal axes. Kxy, Kyz, Kxz are the coupling stiff-
ness of equivalent spring Kx, which reflect responsibility
of spring Kx in three coupling orthogonal axes. And Bxx,
Byy, Bzz are the self-damping of equivalent coefficient Bx,
which reflect the damping effect of Bx in three orthogonal
axes. Bxy, Byz, Bxz are the coupling damping of equivalent
three coupling orthogonal axes.
Substituting Equation (3) into Equation (4), we get the
system of three linear equations in three variables ()
x
x
W,
()
x
y
W,()
x
z
W:
2()
(sincossin )(sin
x() ()
()2 ()()
cos )(sincos )sin
(sincos )(sincossin )(sincos )0
(sincos
x
xxxxx xyxyy xzxzzx
xx
xyxyx yyyyy yzyzz
xz xz
x
x
K
tBtmtW KtBtW KtBtWmat
KtBtWKtBtmtWKtBtW
KtB

   

 


 

()()2 () )(sincos)(sincossin )0
xx
xyzyzy zzzzz
tWKt BtWKtBtmtW 



 


x
(5)
Usually, there are three ponderances of vector accel-
eration, denoted as ,,
x
yz
aaa

. They are responded by the
respective degree o system. Furthermore, re-
sponse along the x, y and z-direction exist in each degree
sions responded to the acceleration signal. In order to
simplify the analysis, damping force is ignored. There-
fore, Equation (5) is simplified to:
f freedom
of freedom system. So there are nine amplitude expres-
C
opyright © 2009 SciRes. ENGINEERING

Y. LIU ET AL.199
0
0
2() () ()
()2 ()
()
()
xxx
()
()()2 ()
()
x
xxxyyxzzx
xxx
xy xyyyyz z
xx x
xz xyz yzzz
K
mW KW KWma
KWKm WK




 
W
KWKWKm W 


 


(6)
Hence,
22
()
22
()
22
()
22
sin
()
cos cos
()
cos cos
()
xxx
x
x
x
xxxx
yx
x
xxxx
zx
x
Km
Wa
Km
K
Wa
Km
K
Wa
Km


















(7)
Likewise, the amplitudes responded to acceleration
signal t
sin, sin
yz
ata


are respectively given by
()
22
cos cos
()
yyy
y
y
Ka
Km




22
()
22
()
22
sin
()
cos cos
()
x
y
yy
y
yy
y
yy
y
y
zy
y
W
Km
Wa
Km
K
Wa
Km















(8 )
And
()
22
()
22
22
()
22
cos cos
()
cos cos
()
sin
()
zzzz
xz
z
zzzz
yz
z
zzz
z
z
z
K
Wa
Km
K
Wa
Km
Km
W
Km














 

a
(9)
3.3. Analysis
previous analysis, we get the nine am-
ons responded to the sinusoidal accelera-
Building on the
litude expressip
tion signal, as listed in Table 1.
For 3-axis microaccelerometer, what we need is the
amplitude response in leading diagonal of Table 1. They
should be the strongest, whereas the others are the cross
disturbance. Therefore, transverse sensitivity of x-axis in
y- and z-direction are given by
2
22
cos cos
sin
ycrossyyy x
yx
SK Km
SSmK
2
22
2
22
cos cos,
sin
cos cos.
sin
y
xcross x x x
xy
yaxial yyx
y
zcross zzz
zy
yaxial yyz
Km
2
2
K
SSmK Km
Km
SK
SSmK Km

S 










 


 

(11)

2
22
2
22
cos cos,
sin
cos cos.
sin
xcrossxxxz
xz
zaxialzz x
ycrossyyy z
yz
zaxialzz y
SK Km
SSmKKm
SK Km
SSmK Km

2
2












 


 

(12)
If the microaccelerometer sensitive to the change in
displacement has three primary axes, then the equation
Kx=Ky=Kz is always expected for uniform sensitivity in
three sense directions. So the expressions of transverse
sensitivity in Equation (10)–(12) could be simplified.
Considering constraints for symmetrical decline angles of
x-, y- and z- degrees of freedom system, that is,,,
x
yz

are all close to zero, it’s not difficult to find that t
sensitivity only relates to the coupling angles and the way
for small transverse sensitivity is to make the coupling
angles equal to
ransverse
2

. Of course, ,
yz


are the coupling
angles of x- systehile , m, w
x
z


and ,
x
y


are those of y-
and z- systems respectivelhe co angles are all
equal to
y. If tupling
2

, then transverse sensitivity S=0.
It shoube pointed out if the microaccelerld
on
ometer has
ly one or two primary axes, then the above six expres-
sions about transverse sensitivity will be decreased by four
or two. For instance, there are only Syx, Szx for x-axis ac-
celerometer. So transverse sensitivity relates not only to the
coupling angles but also to the response stiffness in different
axes. Therefore, two methods are recommended to reduce
transverse sensitivity. One is to make the coupling angles
equal to 2

. The other is to ensure the response stiffness
in the prim axis far less than that in the cross axis. ary
4. Summary
ents a general analysis about transverse This paper pres
2
2
222
,
cos cos .
sin
xa
xialxx y
zcross x zzz
zx
xaxial xxz
Km
SKm
K
SSmKKm





sensitivity of the microaccelerometer. Firstly, the analysis
model for cross disturbance of the microaccelerometer is
developed, where the influence of response stiffness and
damping in different axes, as well as symmetrical decline
angles of 3 degrees of freedom system are considered.
Secondly, multi-freedom vibration equations based on the
analysis model are established. And the equations are
solved on condition that damping force is ignored. Finally,
some effective methods, which are beneficial to reduce
cross disturbance, are provided. For the microaccelerome-











(10)
Similarly,



sensitive to the change in displacement, if it has

Y. LIU ET AL. 200
Table 1. Amplitude responded to the sinusoidal acceleration signal.
Amplitude
Acceleration
x-direction y-direction z-direction
sin
x
at

22
22
sin
()
xx
x
x
Km
a
Km



 22
cos cos
()
xxx
x
x
Ka
Km


 22
cos cos
()
xxx
x
x
Ka
Km



sin
y
at

22
cos cos
()
yyy
y
y
Ka
Km

 
22
22
sin
()
yy
y
y
Km
a
Km



 22
cos cos
()
yyy
y
y
Ka
Km

 
sin
z
at

22
cos cos
()
zzz
z
z
Ka
Km

  22
cos cos
()
zzz
z
z
Ka
Km

 
22
22
sin
()
zz
z
z
Km
a
Km




three primary axes, then transverse sensitivity only relates
to the coupling angle and the way for small transverse
sensitivity is to make the coupling angles equal to 2

. If
it has one or two primary axes, then transverse sensitivity
relates not only to the coupling angle but also to the resp-
onse stiffness in different axes. So in order to reduce
transverse sensitivity, two methods are recommended.
One is to make the coupling angles equal to 2

. The
other is to ensure the response stiffness in the primary axis
far less than that in the cross axis.
5. References
[1] L. Fei, X. X. Zhong, Z. Y. Wen, et al, “Methods for re-
ducing sensitivity of micromachined silicon accelerome-
ter,” Optics and Precision Engineering, No. 3, pp. 64–68,
1995
[2] J. S. Wang, Q. Wang, and S. H. Sun, “Effect of cross-
coupling coefficient of accelerometer on gyros–free iner
tial measurement unit,” Journal of Chinese Inertial Tech-
nology, No. 11, pp. 29–33, 2003.
[3] L. Zhong., J. G. Liu, and H. Y. Zhao, “A solution to the
problem of excessive error of piezoelectrical accelerome-
ter’s cross axis sensitivity,” Electro-Mechanical Engi-
neering, Vol. 20, pp. 4–5, 2004.
[4] Y Liu, Z. Y. Wen, Z. Q. Wen, et al, “Design and fabrication
of a high-sensitive capacitive biaxial microaccelerometer,” J.
Micromech. Microeng, Vol. 17, pp. 36–41, 2007.
[5] Y Liu, Z. Y. Wen, and H. Y. Yang, “Effect of fabrication
characteristic of 2–d microaccelerometer on perform-
ance,” Journal of Functional Materials and Devices, Vol.
14, pp. 331–335, 2008.
[6] Y. Liu, Z. Y. Wen, L. Q. Zhang, et al, “Structure design
and system simulation of 2–d microaccelerometer,”
ISTM05, Vol. 3, pp. 2071–2075.
[7] N. Zeng, “Research on the key technology of fiber optic
accelerometers,” Doctor Thesis, Tsinghua University, pp.
97–100, 2005.
C
opyright © 2009 SciRes. ENGINEERING