Open Journal of Physical Chemistry, 2011, 1, 94-103
doi:10.4236/ojpc.2011.13013 Published Online November 2011 (http://www.SciRP.org/journal/ojpc)
Electrical and Dielectric Characterization of
Na0.5Li0.5Zr2(PO4)3
Umaru Ahmadu1, Tomas Salkus2, Abubakar Ohinoyi Musa3, Kasim Uthman Isah1
1Department of Physics, Federal University of Technology, Minna, Nigeria.
2Faculty of Physics, Vilnius University, Vilnius, Lithuania.
3Department of Physics, Bayero University, Kano, Nigeria.
Received July 11, 2011; revised September 15, 2011; accepted October 16, 2011
Abstract
Na0.5Li0.5Zr2(PO4)3 has been synthesized by solid state reaction and characterized by thermogravimetry/
differential thermal analyses (TGA/DTA) in the temperature range 300 - 1573 K. X-ray diffraction measure-
ments have been carried out to determine the phase of the composition and scanning electron microscopy
(SEM) for microstructure evaluation. Impedance spectroscopy at different temperatures (310 - 600 K) and
frequencies (300 kHz - 1 GHz) have been carried out and the dielectric relaxation behaviour was determined
under the same conditions. A dc conductivity maximum value of 0.25 S/m at 580 K was observed. However,
the mixed alkali effect was not observed. The material exhibited relaxation behaviour with a peak in the
dielectric permitivity '

at 469 K. There were no structural transformations observed.
Keywords: NZP, Impedance Spectroscopy, Dielectric Relaxation, Electrical Conductivity
1. Introduction
At present one of the most important materials under
investigation belongs to the NZP (sodium zirconium ph-
osphate) family of compounds with formula NaZr2
(PO4)3. NZP has many potential applications, which in-
cludes, environmental gas sensors (for detection of pol-
lutant gases like CO2), thermal expansion [1], nuclear
waste immobilization [2,3] and rechargeable lithium ion
batteries. The Na, Zr, and P can be substitutted by atoms
of different sizes and oxidation states resulting in com-
pounds of different physical and chemical properties,
while at the same time retaining the same crystal stru-
cture. Such substitutions have lead to an enhancement of
electrical conductivity [4,5], among other physical pro-
perties. The compound has been synthesized mainly us-
ing the solid state reaction method and ZrO2 is usually
precipitated [6] due to the high temperature required for
the synthesis. Additionally, small impurity phases (Li3
PO4, LiTiPO4, ZrP2O7), among others, have been detec-
ted that do not affect the overall conductivity of the com-
positions [7-9].
The composition Na1-xLixZr2(PO4)3, (where x = 0.0,
0.3, 0.5, 0.7 and 1.0) have been studied by Pet’kov et al.
[10], by using solid state reaction and characterized by
X-ray diffraction and differential thermal analyses (DTA).
Similarly, Naik et al. [11,12] have synthesized NaZr2
(PO4)3 using microwave techniques at lower tempera-
tures and carried out structural characterizations using
XRD. However, the conductivity of NaZr2(PO4)3 has been
reported to be very low, below the applicable range [13].
A key factor in the application of ionic materials in rech-
argeable batteries is that they must have high conduc-
tivity, of the order 101 to 10–1 S/m [14] in operating con-
ditions. Thus studies on partial as well as full substi-
tutions (of Na, Zr and P) have been carried out in order
to improve the conductivities of the compositions. More-
over, most of the impedance spectoscopy (IS) studies of
the compositions have been undertaken within the kHz-
MHz range of frequencies [6,15], wheareas very few stu-
dies have been reported in the GHz range [5,16]. There
are also no reports on their dielectric relaxation pro-
perties.
It is important to know the structure of NZP in order to
understand how substitutions of Na+, Zr4+ or P5+ cations
influence the conductivity. NZP has a hexagonal crystal
structure and belongs to the rhombohedral symmetry
(space group 3Rc). The structure is made up of ZrO6
octahedra and PO4 tetrahedara which share all their
vertices to form interconnected network of channels. Na+

95 U. AHMADU ET AL.
ions are located in these channels and can occupy two
distinct sites, labelled type I (M1) and type II (M2). In
NZP, only the M1 sites are filled and the M2 sites are
empty. In order to correlate electrical parameters, such as
electrical conductivity and associated activation energies
with structural factors, the effect of the size of the bot-
tleneck that connects M1-M2 sites are very important. A
representation of the structure and its detailed description
has been provided by several authors [7,18,19].
It has been observed that when Li+ cations are in these
channnels they become suitable candidates for lithium
rechargeable cells, if their conductivity at room tem-
perature can be enhanced. We hypothesize that partial
substitution of Na+ by Li+ ions in a 50:50 ratio at these
sites should affect the conductivity positively due to their
differencies in radii, mass and mobility and it should
result in low activation energy. The phenomenon of
“mixed alkali effect” has been suspected [7] to be res-
ponsible for the low conductivity and high activation
energy observed in a similar system (that is, when com-
pared with compounds without Li+ ions) in which the
authors suggested that further work is needed to arrive at
a conclusive position.
In the present work we have carried out the synthesis
of Na0.5Li0.5Zr2(PO4)3 using solid state reaction by sin-
tering at 1523 K. TGA/DTA have been carried out on
their powder mixtures (Na2CO3·H2O, NH4H2PO4, Li2CO3
and ZrO2) from room temperature to 1273 K, in order to
determine the decomposition and mass losses (tempe-
rature stabilty) and phase transformations. In addition, IS
and dielectric relaxation relaxation behaviour of the com-
pound have been investigated in the temperature range
310 - 600 K and frequency range 300 kHz - 1 GHz. A
high dc conductivity value was observed and the system
exhibited dielectric behaviour at certain frequencies.
2. Experimental Procedure
Na2CO3·H2O, ZrO2, Li2CO3 and NH4H2PO4 of analytical
grade and purity > 99% were used as starting materials.
Stoichiometric amounts of these materials were mixed
and thoroughly ground (manually) in an agate mortar for
about five hours. The samples were then dried in air for
about four hours. Acetone was added in appropriate qu-
antity to homogenize the mixture. Pellets of discs (which
were dry) of 13 mm diameter and 6 mm thickness were
pressed under pressure of 7.42·106 N/m2 for sintering.
All the samples were placed inside a gas-heated furnace
for eight hours at successive temperatures 573, 773, 1323,
1373, 1423, 1473 and 1523 K, respectively. Between
each temperature the samples were allowed to furnace-
cool to room temperature and then thoroughly re-ground,
re-mixed, pelletized and placed back into the furnace for
the next round of heating. The first two temperatures
were to allow for the volatilization of bye-products, am-
monia, water and carbon dioxide. The other tempera-
tures were to allow for full sintering at a maximum tem-
perature of 1523 K.
Powder specimens were used for the measurement of
thermal analyses on DTA machine Netzsch DTA404PC
in air. The readings were conducted between room tem-
perature and 1273 K at heating rate of 20.0 K/min. Simi-
larly, TGA was performed on specimen powders under
similar conditions on TGA Pyris 6 (Perkin Elmer, USA)
thermal analyser. Both DTA and TGA data were automa-
tically acquired from the machines.
X-ray powder diffraction measurements were carried
out using a precision mini X-ray diffractometer MD-10,
Version 2.0.4 by Radicon Ltd. The 2θ range was 16˚ - 70˚
and the working power was 25 kV using 20 minutes ac-
quisition time and CuKα radiation λ = 1.5406 Å. The
scanning step was 0.05˚. The surfaces of sintered sample
were analysed by SEM working at 5 kV. For the elec-
trical measurements, sample was prepared 6.16 mm2
(electrode surface area) and length 1.5 mm. A home-
made coaxia line has been used to measure impedance
spectra [20]. The control and acquisition of data were
carried out using MathLab software, on an Agilent Net-
work Analyser E5062A in the frequency range from 300
kHz to 1 GHz (at 16 points per decade of frequency) and
temperature range 310 - 600 K. Measurements were per-
formed every 10 K on heating the sample at 1 K per min
using a voltage of 200 mV.
3. Results and Discussion
The XRD pattern for the composition Na0.5Li0.5Zr2(PO4)3
shows minor phase Na5Zr(PO4)3 with ZrO2 detected. Na5
Zr(PO4)3 has been synthesized and characterized by some
workers [21] who reported that it has no specific thermal
effects (for example, phase transformation), though, it
undergoes reversible phase transitions and decomposes at
433 K [21]. We thus assume that there is minimal dis-
tortion to the crystal lattice and thus shows that the syn-
thesized composition is single phase. Impurity phases
have been reported in solid state reactions. Some authors
[18] have observed a distortion to the hexagonal lattice
(in the preparation of NASICON-based compounds) as a
result of presence of some impurity phases (AlPO4, GeO2)
which have been found to be a function of either de-
creasing temperature or of multiple substitutions at spe-
cific lattice sites. The authors assumed the effect of these
impurities to be negligble on the overall crystal structure.
The compound under investigation (Na0.5Li0.5Zr2(PO4)3 )
was also indexed based on the hexagonal lattice structure
and found to belong to the rhombohedral crystal sym-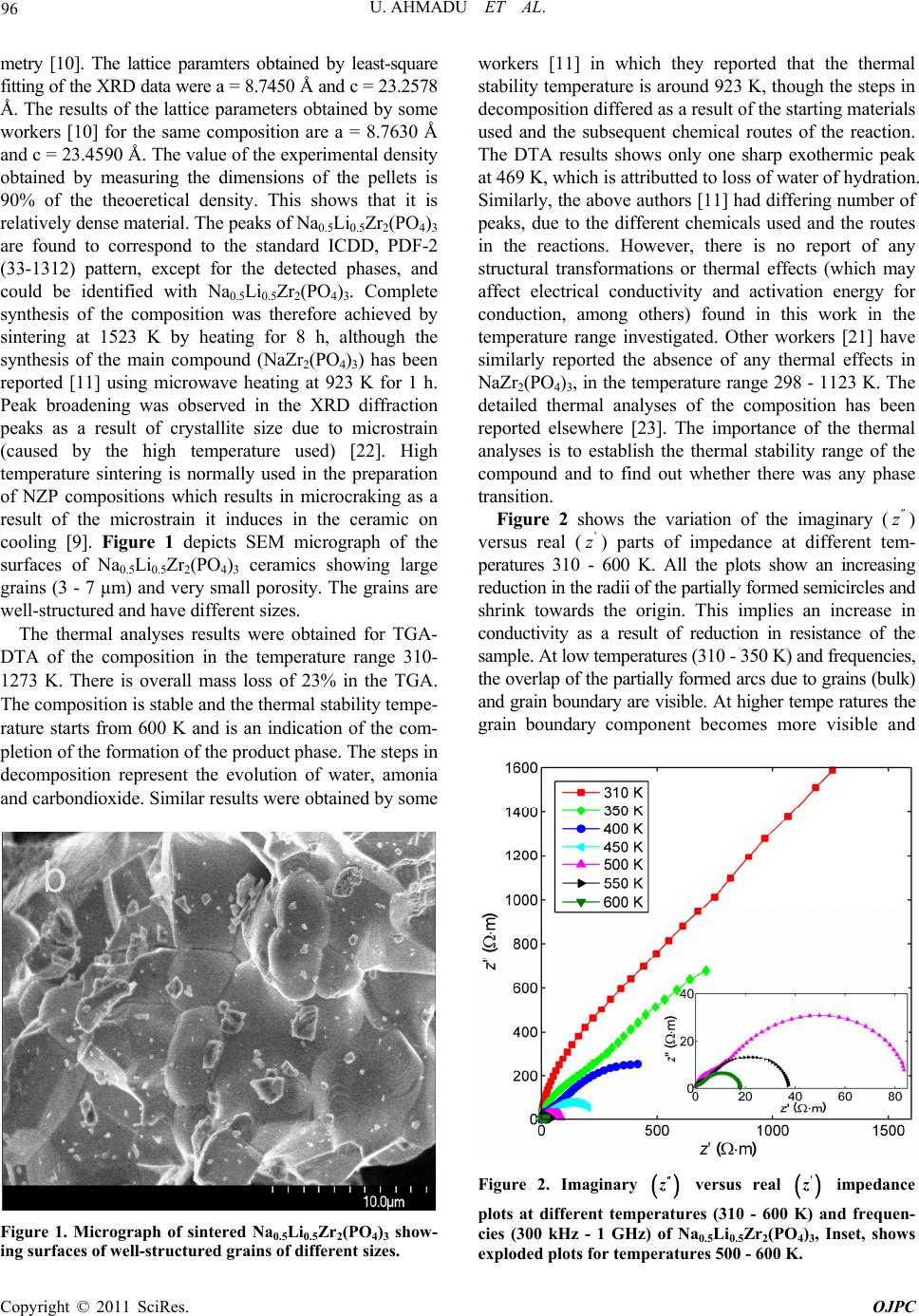

U. AHMADU ET AL.
96
metry [10]. The lattice paramters obtained by least-square
fitting of the XRD data were a = 8.7450 Å and c = 23.2578
Å. The results of the lattice parameters obtained by some
workers [10] for the same composition are a = 8.7630 Å
and c = 23.4590 Å. The value of the experimental density
obtained by measuring the dimensions of the pellets is
90% of the theoeretical density. This shows that it is
relatively dense material. The peaks of Na0.5Li0.5Zr2(PO4)3
are found to correspond to the standard ICDD, PDF-2
(33-1312) pattern, except for the detected phases, and
could be identified with Na0.5Li0.5Zr2(PO4)3. Complete
synthesis of the composition was therefore achieved by
sintering at 1523 K by heating for 8 h, although the
synthesis of the main compound (NaZr2(PO4)3) has been
reported [11] using microwave heating at 923 K for 1 h.
Peak broadening was observed in the XRD diffraction
peaks as a result of crystallite size due to microstrain
(caused by the high temperature used) [22]. High
temperature sintering is normally used in the preparation
of NZP compositions which results in microcraking as a
result of the microstrain it induces in the ceramic on
cooling [9]. Figure 1 depicts SEM micrograph of the
surfaces of Na0.5Li0.5Zr2(PO4)3 ceramics showing large
grains (3 - 7 µm) and very small porosity. The grains are
well-structured and have different sizes.
The thermal analyses results were obtained for TGA-
DTA of the composition in the temperature range 310-
1273 K. There is overall mass loss of 23% in the TGA.
The composition is stable and the thermal stability tempe-
rature starts from 600 K and is an indication of the com-
pletion of the formation of the product phase. The steps in
decomposition represent the evolution of water, amonia
and carbondioxide. Similar results were obtained by some
Figure 1. Micrograph of sintered Na0.5Li0.5Zr2(PO4)3 show-
ing surfaces of well-structured grains of different sizes.
workers [11] in which they reported that the thermal
stability temperature is around 923 K, though the steps in
decomposition differed as a result of the starting materials
used and the subsequent chemical routes of the reaction.
The DTA results shows only one sharp exothermic peak
at 469 K, which is attributted to loss of water of hydration.
Similarly, the above authors [11] had differing number of
peaks, due to the different chemicals used and the routes
in the reactions. However, there is no report of any
structural transformations or thermal effects (which may
affect electrical conductivity and activation energy for
conduction, among others) found in this work in the
temperature range investigated. Other workers [21] have
similarly reported the absence of any thermal effects in
NaZr2(PO4)3, in the temperature range 298 - 1123 K. The
detailed thermal analyses of the composition has been
reported elsewhere [23]. The importance of the thermal
analyses is to establish the thermal stability range of the
compound and to find out whether there was any phase
transition.
Figure 2 shows the variation of the imaginary (z

)
versus real () parts of impedance at different tem-
peratures 310 - 600 K. All the plots show an increasing
reduction in the radii of the partially formed semicircles and
shrink towards the origin. This implies an increase in
conductivity as a result of reduction in resistance of the
sample. At low temperatures (310 - 350 K) and frequencies,
the overlap of the partially formed arcs due to grains (bulk)
and grain boundary are visible. At higher tempe ratures the
grain boundary component becomes more visible and
'
z
Figure 2. Imaginary


z

versus real impedance
plots at different temperatures (310 - 600 K) and frequen-
cies (300 kHz - 1 GHz) of Na0.5Li0.5Zr2(PO4)3, Inset, shows

'
z
exploded plots for temperatures 500 - 600 K.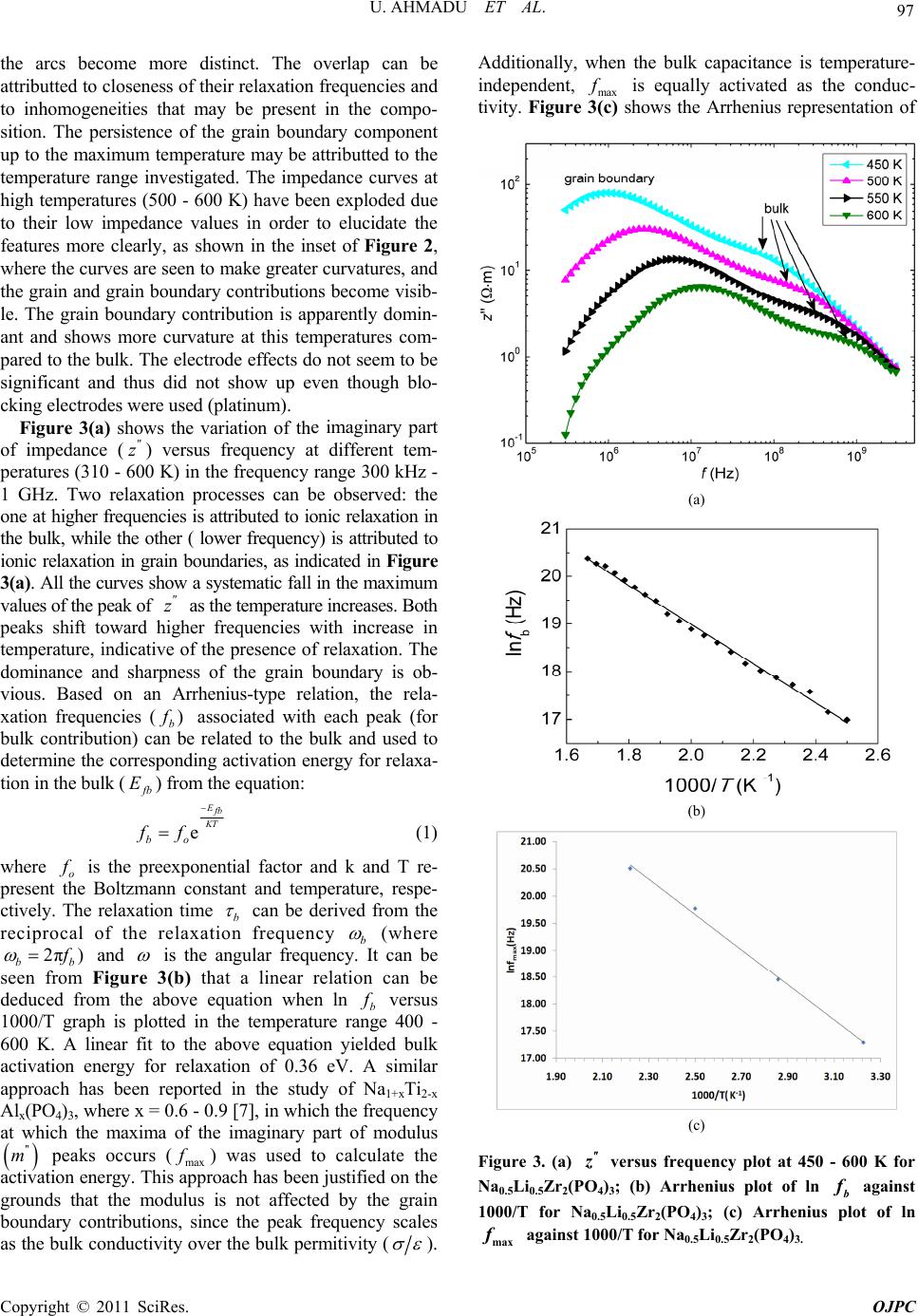

U. AHMADU ET AL. 97
rlap can be
e imaginary part
of
the arcs become more distinct. The ove
attributted to closeness of their relaxation frequencies and
to inhomogeneities that may be present in the compo-
sition. The persistence of the grain boundary component
up to the maximum temperature may be attributted to the
temperature range investigated. The impedance curves at
high temperatures (500 - 600 K) have been exploded due
to their low impedance values in order to elucidate the
features more clearly, as shown in the inset of Figure 2,
where the curves are seen to make greater curvatures, and
the grain and grain boundary contributions become visib-
le. The grain boundary contribution is apparently domin-
ant and shows more curvature at this temperatures com-
pared to the bulk. The electrode effects do not seem to be
significant and thus did not show up even though blo-
cking electrodes were used (platinum).
Figure 3(a) shows the variation of th
impedance (z) versus frequency at different tem-
peratures (310 - 60 K) in the frequency range 300 kHz -
1 GHz. Two relaxation processes can be observed: the
one at higher frequencies is attributed to ionic relaxation in
the bulk, while the other ( lower frequency) is attributed to
ionic relaxation in grain boundaries, as indicated in Figure
3(a). All the curves show a systematic fall in the maximum
values of the peak of z as the temperature increases. Both
peaks shift toward hher frequencies with increase in
temperature, indicative of the presence of relaxation. The
dominance and sharpness of the grain boundary is ob-
vious. Based on an Arrhenius-type relation, the rela-
xation frequencies ()
b
0
ig
f
associated with each peak (for
bulk contribution) cae related to the bulk and used to
determine the corresponding activation energy for relaxa-
tion in the bulk (
n b
f
b
E) from the equation:
e
E
f
b
K
T
bo
ff (1)
where

o
f
is the preexponential factor and k and T re-
present the Boltzmann constant and temperature, respe-
ctively. The relaxation time b

can be derived from the
reciprocal of the relaxatio frequency b n

(where
2π)
bb
f

 and

is the angular frequencyt can be
Figur 3(b) that a linear relation can be
deduced from the above equation when ln b
. I
seen from e
f
versus
1000/T graph is plotted in the temperature range 400 -
600 K. A linear fit to the above equation yielded bulk
activation energy for relaxation of 0.36 eV. A similar
approach has been reported in the study of Na1+xTi2-x
Alx(PO4)3, where x = 0.6 - 0.9 [7], in which the frequency
at which the maxima of the imaginary part of modulus

''
m peaks occurs (max
f
) was used to calculate the
tion energy. This oach has been justified on the
grounds that the modulus is not affected by the grain
boundary contributions, since the peak frequency scales
as the bulk conductivity over the bulk permitivity (
activa appr

 ).
Additionally, when the bulk capacitance is temperature-
independent, max
f
is equally activated as the conduc-
tivity. Figure ows the Arrhenius representation of
3(c) sh
(a)
(b)
(c)
Figure 3. (a)
z

O4
versus frequency plot at 450 - 600 K for
Na0.5Li0.5Zr2(P )3; (b) Arrhenius plot of ln b
f against
1000/T for Na0.5Li0.5Zr2(PO4)3; (c) Arrhenius plot of ln
max
f against 1000/T for Na0.5Li0.5Zr2(PO4)3.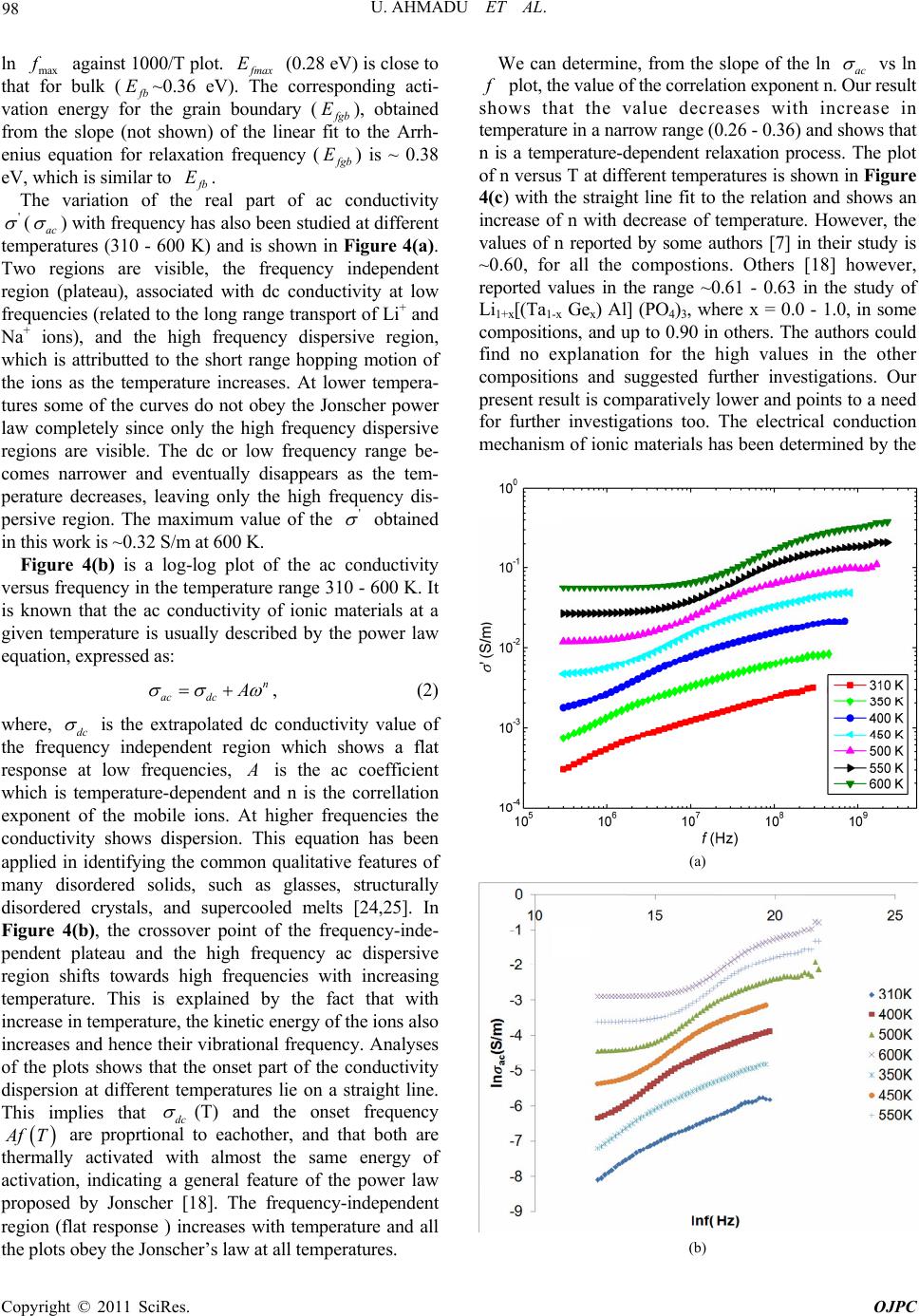

U. AHMADU ET AL.
98
ln max
f
against 1000/T plot.
f
max
E (0.28 eV) is close to
tha bulk (t for
f
b
E~0.36 eV) corresponding acti-
vation energy fhe grain boundary (
. The
or t
f
gb
E), obtained
from the slope (not shown) of the linear the Arrh-
enius equation for relaxation frequency (
fit to
f
gb
E) is ~ 0.38
eV, which is similar to
f
b
E.
The variation of theal part
'
e r of ac conductivity

(ac

) with frequency has also been studied at different
ptures (310 - 600 K) and is shown in Figure 4(a).
Two regions are visible, the frequency independent
region (plateau), associated with dc conductivity at low
frequencies (related to the long range transport of Li+ and
Na+ ions), and the high frequency dispersive region,
which is attributted to the short range hopping motion of
the ions as the temperature increases. At lower tempera-
tures some of the curves do not obey the Jonscher power
law completely since only the high frequency dispersive
regions are visible. The dc or low frequency range be-
comes narrower and eventually disappears as the tem-
perature decreases, leaving only the high frequency dis-
persive region. The maximum value of the '
tem era

obtained
in this work is ~0.32 S/m at 600 K.
Figure 4(b) is a log-log plot of the ac conductivity
versus frequency in the temperature range 310 - 600 K. It
is known that the ac conductivity of ionic materials at a
given temperature is usually described by the power law
equation, expressed as:
ac
n
dc
A

 ,  (2)
where, dc

uen
is the extrapolated dc conductivity value of
the freqcy independent region which shows a flat
response at low frequencies,
A
is the ac coefficient
which is temperature-dependentnd n is the correllation
exponent of the mobile ions. At higher frequencies the
conductivity shows dispersion. This equation has been
applied in identifying the common qualitative features of
many disordered solids, such as glasses, structurally
disordered crystals, and supercooled melts [24,25]. In
Figure 4(b), the crossover point of the frequency-inde-
pendent plateau and the high frequency ac dispersive
region shifts towards high frequencies with increasing
temperature. This is explained by the fact that with
increase in temperature, the kinetic energy of the ions also
increases and hence their vibrational frequency. Analyses
of the plots shows that the onset part of the conductivity
dispersion at different temperatures lie on a straight line.
This implies that dc
a

(T) and the onset frequency

A
fT are proprtion l to eachother, and that both are
thlly activated with almost the same energy of
activation, indicating a general feature of the power law
proposed by Jonscher [18]. The frequency-independent
region (flat response ) increases with temperature and all
the plots obey the Jonscher’s law at all temperatures.
We can determine, from the slope of the ln ac
a
erma

vs ln
f plot, the value of the correlation exponent n. Our result
tem
(b)
shows that the value decreases with increase in
perature in a narrow range (0.26 - 0.36) and shows that
n is a temperature-dependent relaxation process. The plot
of n versus T at different temperatures is shown in Figure
4(c) with the straight line fit to the relation and shows an
increase of n with decrease of temperature. However, the
values of n reported by some authors [7] in their study is
~0.60, for all the compostions. Others [18] however,
reported values in the range ~0.61 - 0.63 in the study of
Li1+x[(Ta1-x Gex) Al] (PO4)3, where x = 0.0 - 1.0, in some
compositions, and up to 0.90 in others. The authors could
find no explanation for the high values in the other
compositions and suggested further investigations. Our
present result is comparatively lower and points to a need
for further investigations too. The electrical conduction
mechanism of ionic materials has been determined by the
(a)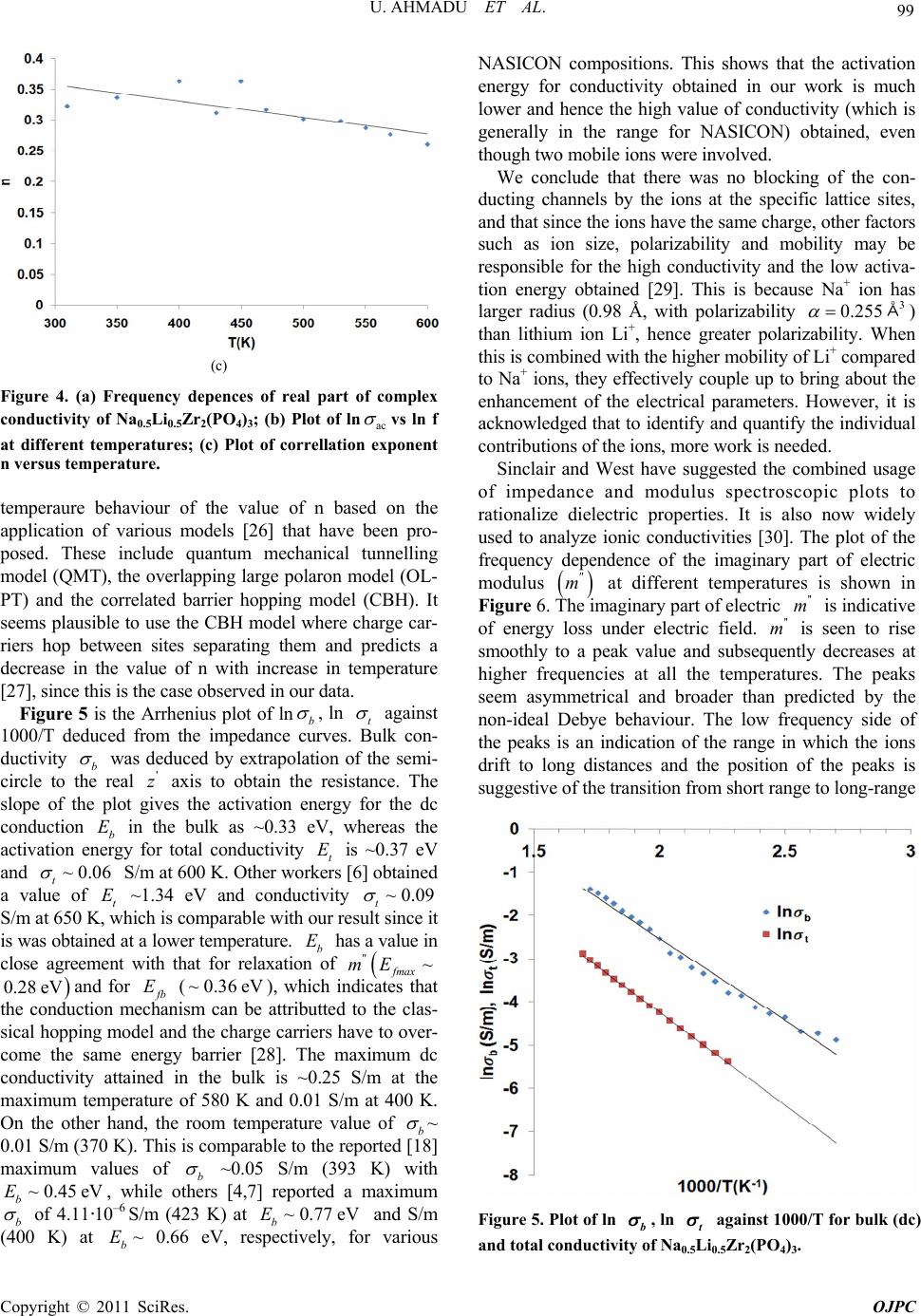

U. AHMADU ET AL. 99
(c)
Figure 4. (a) Frequency depences of real part of complex
conductivity of NaLi Zr ); (b) Plot of ln
0.50.5243
(PO ac

vs ln f
at different temperatures; (c) Plot of correllationonent
n versus temperature.
temperaure behaviour of the value of n based on the
application of various models [26] that have been pro-
posed. These include quantum mechanical tunnelling
model (QMT), the overlapping large polaron model (OL-
PT) and the correlated barrier hopping model (CBH). It
seems plausible to use the CBH model where charge car-
riers hop between sites separating them and predicts a
decrease in the value of n with increase in temperature
[27], since this is the case observed in our data.
Figure 5 is the Arrhenius plot of ln
exp
b

, ln t

agai
curves. Bulk con
nst
1000/T deduced from the edance-imp
ductivity b

was deduced by extrapolation of the semi-
circle to the real '
z axis to obtain the resistance. The
slope of the plot gives the activation energy for the dc
conduction b
E in the bulk as ~0.33 eV, whereas the
activation energy for total conductiveV ity t
E is ~0.37
and ~0.06
t

S/m at 600 K. Other workers [6] obtained
a value of t
E ~1.34 eV and conductivity ~0.09
t

S/m at 650 K, which is comparable with our result since it
is was obtained at a lower temperature. b
E has a value in
close agreement with that for relaxation of

~
fmax
mE


0.28 eVand for
f
b
E (~0.36eV), which indicates that
the conduction mechanism can be attributted to the clas-
sical hopping model and the charge carriers have to over-
come the same energy barrier [28]. The maximum dc
co ~0nductivity attained in the bulk is .25 S/m at the
maximum temperature of 580 K and 0.01 S/m at 400 K.
On the other hand, the room temperature value of b

~
0.01 S/m (370 K). This is comparable to the reported [18]
maximum values of b

~0.05 S/m (393 K) with
~0.45eV
b
E, while others [4,7] reported a maximum
b

of 4.11·10–6 S/m (423 K) at ~0.77eV
b
E and S/m
(400 K) at b
E~ 0.66 eV, respectively, for various
NASICON copositions. This shows that the
energy for conductivity obtained in our work is much
lower and hence the high value of conductivity (which is
generally in the range for NASICON) obta
o mobiles wved.
We conclude that there was no blocking of the con-
ducting channels by the ions at the specific lattice sites,
and that since the ions have the same charge, other factors
such as ion size, polarizability and mobility may be
responsible for the high conductivity and the low activa-
tion energy obtained [29]. This is because Na+ ion has
larger radius (0.98 Å, with polarizability 3
0.255  Å)
than lithium ion Li+, hence greater polarizability. When
ed with the higher mobility of Li+ compared
Na+ ions, they effectively coup about the
enhancement of the electrical parameters. However, it is
acknowledged that to identify and quantify the individual
contributions of the ions, more work is needed.
Sinclair and West have suggested the combined usage
of impedance and modulus spectroscopic plots to
rationalize dielectric properties. It is
m activation
ined, even
though tw ionere invol
this is combin
to le up to bring
also now widely
used to analyze ionic conductivities [30]. The plot of the
frequency dependence of the imaginary part of electric
modulus


m

at different temperatures is shown in
Figure 6. The imaginary part of electric '' m is indicative
of energy loss under electric field. '' m is seen to rise
smoothly to a peak value and subsequently decreases at
higher frequencies at all the temperatures. Ths
seem asymmetrical and broader than predicted by the
non-ideal Debye behaviour. The low frequency side of
the peaks is an indication of the range in which the ions
drift to long distances and the position of the peaks is
suggestive of the transition from short range to long-range
e peak
Figure 5. Plot ob

and total co
, ln t

f ln against 1000/T for bulk (dc)
nductivity of Na0.5Li0.5Zr 2(PO4)3.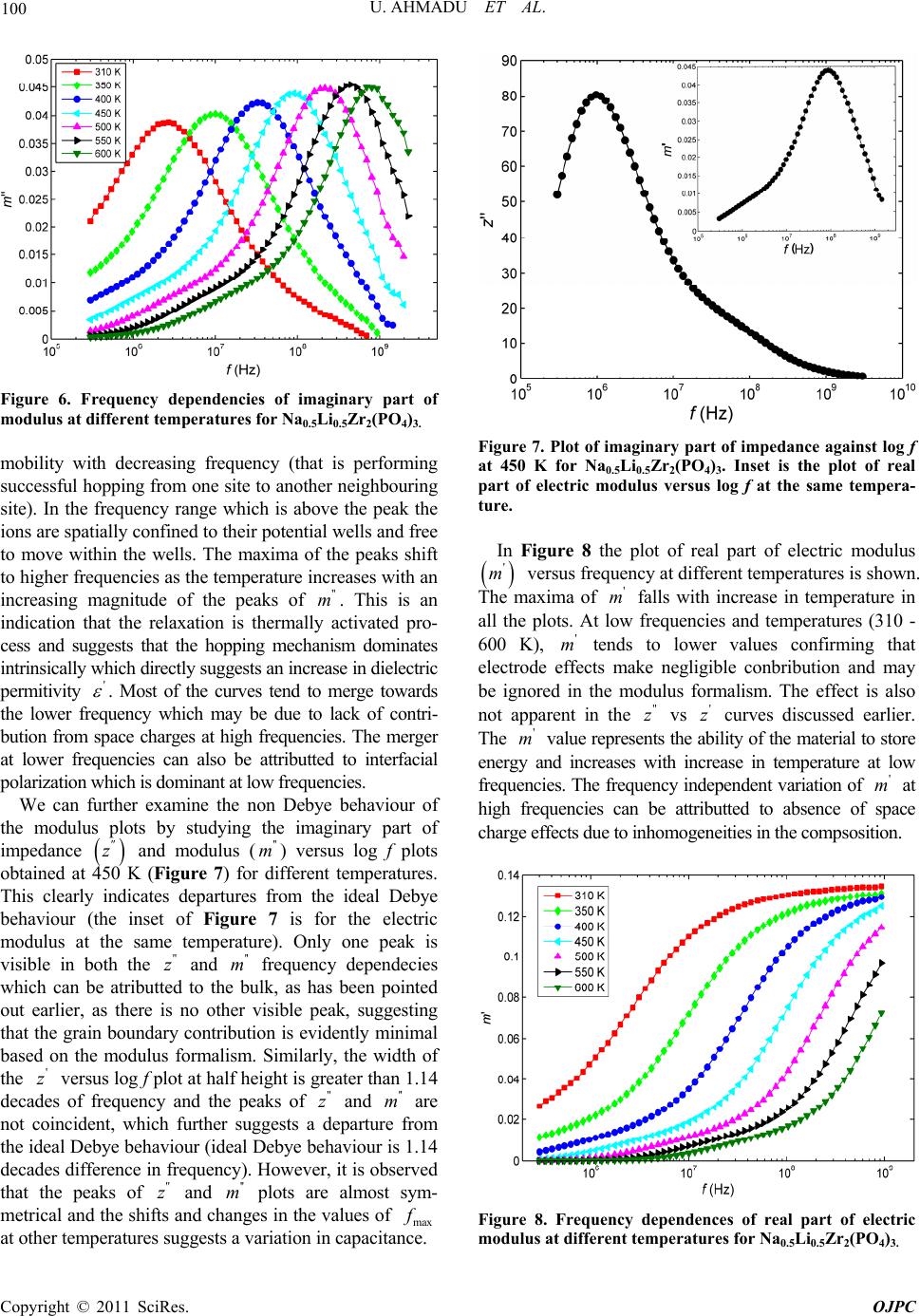

U. AHMADU ET AL.
100
Figure 6. Frequency dependencies of imaginary part of
modulus at different temperatures for Na0.5Li0.5Zr2(PO4)3.
r
neighbouring
site). In the frequency range which is above the peak the
ions are spatially confined to their potential wells and free
to move within the wells. The maxima of the peaks shift
to higher frequencies as the temperature increases with an
increasing magnitude of the peaks of . This is an
indication that the relaxation is thermtivated pro-
cess and suggests that the hopping me dominates
intrinsically which directly suggests an in in dielectric
permitivity
mobility with decreasing fequency (that is performing
successful hopping from one site to another
''
m
ally a
chanism
creas
c
e
'

. Most of the curves tendrge towards
the lowerequency which may be du lack of contri-
bution from space charges at high frequencies. The merger
at lower frequencies can also be attributted to interfacial
polarization which is dominant at low frequencies.
We can further examine the non Debye behaviour of
s
btained at 7) for different temp
at
to me
e to fr
the modulus plots by studying the imaginary part of
impedance

z and modulus ('' m) versus log f plot
o 450 K (Figure eratures.
f f
This clearly indicates departures from the ideal Debye
behaviour (the inset of Figure 7 is for the electric
modulus at the same temperature). Only one peak is
visible in both the " z and '' m frequency dependecies
which can be atributted to the bulk, as has been pointed
out earlier, as there is no other visible peak, suggesting
that the grain boundary contribution is evidently minimal
based on the modulus formalism. Similarly, the width of
the ' z versus log f plot at half height is greater than 1.14
decades of frequency and the peaks of " z and '' m are
not coincident, which further suggests a departure from
the ideal Debye behaviour (ideal Debye behaviour is 1.14
decades difference in frequency). However, it is observed
that the peaks of " z and '' m plots are almost sym-
metrical and the shifts and changes in the values omax
other temperatures suggests a variation in capacitance.
Figure 7. Plot of imaginary part of impedance againstf
at 450 K for Na0.5Li0.5Zr2(PO4)3. Inset is the plot of real
part of electric modulus versus log f at the same tempera-
log
ture.
In Figure 8 the plot of real part of electric modulus


'
m
The ma
all
600 K
be igno
not ap
The m
energy
freque
high
versus frequency at different temperatures is shown.
xima of falls with increase in temperature in
the plots. At low frequencies and temperatures (310 -
) tends to lower values confirming that
ke negligible conbribution and may
odulus formalism. The effect is also
n curves discussed earlier.
rity of the material to store
crse in temperature at low
ent variation of at
tted to absence of ace
charge effects due to inhomogeneities in the compsosition.
'
m
ma
m
the
epres
eases
cies can b
, ' m
electrode effects
parent i
valu
and in
ncies. The fr
frequen
red in the
e
"
z vs
ents the
with in
equency
e attr
'
z
abil
crea
independ
ibu
'
'
m
sp
Figure 8. Frequency dependences of real part of eltric
modulus at different temperatures for Na0.5Li0.5Zr2(PO4)3.
ec

U. AHMADU ET AL. 101
dielectric permitivity
In Figure 9(a) the plot of the variation of real part of
'

K is s
is due to
polarizations,
gligible
y in the low
vs frequency in the temperature
range 310 - 600 hown. The dielectric constant
response of a system electronic, ionic, dipole and
space charge among others. The space
charge effects are neat very low temperatures and
noticeable onlfrequency region. Peaks are
observed in the '

fre
ion. The relevant
y
values fr
itivity inc
ase transitions
ral causes, su
om 400 - 600 K which shift
towards higherquencies with increase in temperature,
this is evidence of the presence of relaxation in the system.
The dielectric permreases with temperature at
low frequencies before it reaches a peak. Peak maxima
have been attributted to several factors, among which is
feroelectric ph[28] and to the begining of
crystallizat dielectric mechanism could
be due to sevech as dipole polarization due
to the frequenc range in which the peak occurs and the
fact that the loss factor ''

peaks fall in this range. At all
the temperatures under investigation, '

decreases with
increase in frequency above the maxima. The decrease is
significant especially at low frequencies, asociated with
the presence of mobile Li+ and Na+ ion polarization. On
the otherhand, the increasing value of '

at low
frequencies can result from charge accumulation at the in-
terface, thus the low frequency dispersion of '

gra-
dually increases with increase in temperature due to an
increase in the interfacial polarization, as well as thermal
activation associated with the mobile ions. The interfacial
polarization is insignificant at high frequencies and hence
'

remains relatively constant [31]. When the tempe-
rature rises the dielectric dispersion shifts to higher fre-
quencies. At high frequencies '

also decreases due to
the high frequency of the field which reduces the
contribution of the charge carries towards the dielectric
permitivity '

and tends to a static value at all tempe-
ratures as a result of absence of space charge effects. In
the temperature range 310 - 400 K, there are no peaks
owing to the frequency range investigated. At 550 and
600 K, the peaks are broad and reflect the distribution of
relaxtion times in the system.
Figure 9(b) shows the variation of imaginary part of
dielectric permitivity

"

as a function of fruency in
the temperature range 310 - 600 K. We observe that ''
eq

decreases with increase in frequency at all the mpe-
ratures under study. It has been generally postulated that
the contribution to the dielectric loss consists of both the
conduction and relaxation components. Thus the imagi-
nary part of dielectric loss has been explained based on
e
te
th ''
dco ac
w

 , where o

is vaccum dielectric
constant, 2πf

 is angular frequency and ''
ac

is the
dielectric loss due to relaxation pocess. The higher value
of ''
r

at relatively low frequency may be attributted to
the contribution arising from both the conduction and
relaxation losses. At higher frequencies however, relaxa-
tion losses are the only sources of dielectric loss. We also
notice that ''

increases with increase in temeprature
because as the relaxation loss component reduces the
conduction loss component increases more rapidly [30].
Further, it is seen that at a ''

ll temperatures values
approach a static value close to zero at higher frequencies.
The temperature dependence of '

was also inves-
tigated in the temperature range 310 - 600 K and frequency
range 0.3 MHz - 1 GH (Figure 9(c)). It is observed that at
high frequency (1 GHz) the material shows an almost
temperature-independent behaviour due to the cessation of
interfacial polarization and absence of space charge effects.
The capacitance of the bulk is almost independent of
tempent seen in ' erature and the slight increm

is due to
ion migrawever, at lower temperatures, all the ti Hoon.
(a)
(b)

U. AHMADU ET AL.
102
(c)
Figure 9. (a) Plots of real and imaginary parts of dielectric
permitivity against frequenc different temperatures for y at
Na0.5Li0.5Zr2(PO4)3; (b) Imaginary part of dielectric permi-
tivity against frequency at different temperatures for the
same composition; (c) Real part of dielectric permitivity
against temperature at different frequencies (0.3 MHz - 1
GHz).
plots show sharp increase in '

with increase in tempe-
rature, particularly at 0.3 - 10 MHz. At other frequencies
(0.3 - 0.54 MHz ) the plots also attain sharp peaks in the
value of '

at 460 K. The increase in '

leading to the
peak can be attributted to interfacial polarization and to
the beggining of crystallization [32]. During the crystal-
lization process the interfaces that would be created bet-
ween the cryststallites with different dielectric constants and
conductivities could be the origin of charge accumulation
and interfacial polarization. However, the subsequent decr-
ease in the value of '

above 460 K is due to reduction of
interfacial polarizatiand loo.
the electrical and dielectric properties of mixed
lkali ions (Li+, Na+) in the composition NaLi Zr
on w ionic mbility
4. Conclusions
We have used multiple characterization methods (TGA/
DTA, XRD/SEM and IS) for the the purpose of inves-
tigating
a0.5 0.52
(PO4)3. A high value of b

was observed which shows
that the conducitvity enhancement was due to higher mo-
bility and polarizability of the mobile ions. The thermal
studies showed that there is no significan thermal effects
as to affect structural phase change which can affect the
conductivity in the temperature and frequency range
investigated. A dc conductivity maximum of 0.25 S/m
was obtained at 580 K which is within the application
range. The variation of the dielectric permitivity showed
that the material exhibited dielectric relaxation properties
at specific frequencies and temperatures (450 - 600 K).
Also, peaks were observed in the tempera
t
ture depen-
itivity around 469 K.
. References
dence of the dielectric perm
5
[1] B. Angadi, V. M. Jali, M. T. Lagare, N. S. Kini, A. M.
Umarji, R. Kumar, S. K. Arora and D. Kanjilal, “50 MeV
Li3+ Irradiation Effects on the Thermal Expansion of
Ca1_xSrxZr4P6O24,” Nuclear Instruments and Methods in
Physics Research B, Vol. 187, No. 1, 2002, pp. 87-94.
doi:10.1016/S0168-583X(01)00847-3
[2] S. Kormaneni, E. Lenain and R. Roy, “Thermal Expan-
sion of NH4Zr2(PO4)3,” Journal of Materials Science
Letters, Vol. 5, No. 1, 1986, pp. 1-3.
doi:10.1007/BF01671415
[3] I. W. Donald, B. L. Metcalfe and R. N. J. Taylor, “The
Immobilization of High Level Radioactive Wastes Using
Ceramics and Glasses,” Journal of Materials Science,
Vol, 32, No. 22, 1997, pp. 5851-5887.
doi:10.1023/A:1018646507438
[4] N. Anantharamulu, G. Prasad and M. Vithal, “Preparation,
Characterization and Conductivity Studies of Li3–2xAl2–x
Sbx(PO4)3,” Bulletin of Materials Science, Vol. 31,
2008, pp.133-138.
No. 2,
doi:10.1007/s12034-008-0023-3
indune, Z. Kanepe, J. Ronis, A. Kažeonis
liukas, “Synthesis Structure and Electric
[5] T. Ŝalkus, A. D
and A. E. Or
Properties of L1+xScxZ2-x(PO4)3(x = 0.1,0.2,0.3),” Lithua-
nian Journal of Physics, Vol. 46, 2006, pp. 361-366.
doi:10.3952/lithjphys.46314
[6] H. Kang and N. Cho, “Phase Formation, Sintering Be-
havior, and Electrical Characteristics of NASICON Com-
pounds,” Journal of Materials Science, Vol. 34, No. 2
1999, pp. 5005-5013. doi:10.1023/A:10
0,
04784327302
[7] F. E. Mouahid, M. Zahir, P. M. Maldonado-Manso, S.
Bruque, E. R. Losilla, M. A. G. Aranda, A. Rivera, C.
Leona and J. Santamaria, “Na-Li Exc
Al (PO )(0.6 ≤ x ≤ 0.9) N
hange of Na1+xTi2-x
x4 3ASICON Series: A Rietveld
and Impedance Study,” Journal of Materials Chemistry,
Vol. 11, 2001, pp. 3258-3263. doi:10.1039/b102918p
[8] K. Oda, S. Takase and Y. Shimizu, “Preparation of High
Conductive Lithium Ceramic,” Material
Vol. 544-545, 2007, pp. 1033-1036.
s Science Forum,
doi:10.4028/www.scientific.net/MSF.544-545.1033
[9] P. S. Tantri, K. Greetha, A. M. Umarji and S. K. Rama-
sesha, “Thermal Expansion Behaviour of Barium and
Strontium Zirconium Phosphates,” Bulletin of Materials
Science, Vol. 23, No. 6, 2000, pp. 491-499.
doi:10.1007/BF02903889
[10] V. I. Petkov, A. I. Orlova, I. G. Trucbach, Y. A. Asabina,
V. T. Demarin and V. S. Kurazhkovskaya, “Immobili
tion of Nuclear Waste Mate
za-
rials Containing Different
Alkali Elements in Single-Phase NZP-Based Ceramics,”
Czech Journal of Physics, Vol. 53, No. 1, 2003, pp. A639
-A648. doi:10.1007/s10582-003-0082-z
A. H. Naik, N. V. Thakkar, S. R. Darwatkar, K. D.[11] S.
Mudher and V. V. Venagopal, “Microwave Assisted Low

U. AHMADU ET AL.
103
the Leachability of
Temperature Synthesis of Sodium Zirconium Phosphate
(NaZr2(PO4)3),” Journal of Thermal Analysis and Calo-
rimetry, Vol. 76, 2004, pp. 707-713.
[12] A. H. Naik, S. S. Deb, A. B. Chalke, M. K. Saxena, K. L.
Ramakumar, V. Venugopal and S. R. Dharwadkar,
“Microwave-Assisted Low Temperature Synthesis of So-
dium Zirconium Phosphate (NZP) and
Some Selected Fission Products Incorporated in Its S truc-
ture―A Case Study of Leachability of Caesium,”
Journal of Chemical Science, Vol. 122, No. 1, 2010, pp.
71-82. doi:10.1007/s12039-010-0009-8
[13] H. Aono, “Studies on Li+ Ionic Conducting
trolyte Composed of Na
Solid Elec-
sicon-Type Structure,” Ph.D
NASICON Ce-
.
Dissertation, Osaka University, Osaka, 1994.
[14] J. Kawamura, N. Kuwata, K. Hattori and J. Misuzaki,
“Ionic Transport in Nanohetergenous Materials,” Reports
of the Institute of Fluid Science, Vol. 19, 2007, pp. 1-2.
[15] J. S. Lee, C. M. Chang, Y. I. Lee, J. H. Lee and S. H.
Hong, “Spark Plasma Sintering (SPS) of
ramics,” Journal of American Ceramic Society, Vol. 87,
No. 2, 2004, pp. 305-307.
doi:10.1111/j.1551-2916.2004.00305.x
[16] E. Kazakevičius, A. F. Orliukas, A. L. Kežionis, A. L.
Jucius, A. Dindune, Z. Kanepe and J. Ronis, “Synthesis
Li
and Electrical Properties of Li1+xZr2-2xAlxTix(PO4)3,”
Materials Science (Medžiagotyra), Vol. 10, 2004, p. 305.
[17] P. Khatri, B. Behera, V. Srivanus and R. N. P. Choudhary,
Complex Impedance Spectroscopic Properties of Ba3V2
O8 Ceramics,” Research Letters in Materials Science,
2008, p. 3.
[18] C. J. Leo, G. V. S. Rao and B. V. R. Chowdari, “Fast Ion
Conduction in the Li-Analogues of Nasicon, 1+x
[(Ta1-2xGex)Al](PO4)3,” Journal of Materials Chemistry,
Vol. 12, No. 6, 2002, pp.1848-1853.
doi:10.1039/b110863h
[19] D. A. Woodcock, P. Lightfoot and R. I. Smith, “Powder
Neutron Diffraction Studies of Three Low Thermal Ex-
pansion Phases in the NZP Family: K0.5Nb0.5Ti1.5-
(PO4)3, Ba0.5Ti2(PO4)3 and Ca0.25Sr0.25-Zr2(PO4)3,”
Journal of Materials Chemistry, Vol. 9, No. 10, 1999, pp.
2631-2636. doi:10.1039/a903489g
[20] A. Kežionis, E. Kazakevičiu
“Broadband High Frequency Impedan
s, T. Šalkus and A. Orliukas
ce Spectrometer
ristics of NASICON
rization of NZP Com-
,
with Working Temperatures up to 1200 K,” Solid State
Ion, Vol. 188, 2010, pp. 110-113.
[21] V. I. Pet’kov, E. A. Asabina, A. V. Markin and N. N.
Smirnova, “Synthesis, Characterization and Thermodyna-
mic Data of Compounds with NZP Structure,” Journal of
Thermal Analysis and Calorimetry, Vol. 91, 2008, pp.
157-158.
[22] D.-M. Zhu, F. Luo, Z.-L. Xie and W.-C. Zhou, “Phase
Formation and Electrical Characte
Ceramics,” Transactions of Nonferrous Metal Society of
China, Vol. 17, 2007, pp. s1156-s1159.
[23] U. Ahmadu, A. O. Musa, S. A. Jonah and N. Rabiu,
“Synthesis and Thermal Characte
pounds Na1-xLixZr2(PO4)3 (x = 0.00-0.75),” Journal of
Thermal Analysis and Calorimetry, Vol. 101, 2010, pp.
175-179. doi:10.1007/s10973-010- 0679-y
[24] C. S. Sunandana and P. S. Kumar, “Theoretical App-
roaches to Superionic Conductivity,” Bulletin of Ma-
terials Science, Vol. 27, No. 1, 2004, pp. 1-17.
doi:10.1007/BF02708477
[25] J. Bisquert, V. Halpern and F. Henn, “Simple Model for
AC Ionic Conduction in Solid,” Journal of Chemical
Physics, Vol. 122, No. 15, 2005, pp. 151101-1-151101-4.
doi:10.1063/1.1896359
[26] A. Gosh, “AC Conduction in Iron Bismuthate Glassy
Semiconductors,” Physical Review B, Vol. 42, No. 2,
1990, pp. 1388-1393. doi:10.1103/PhysRevB.42.1388
0, pp. 67-
9-0333-5
[27] A. Jarboui, A. Ben Rhaeim, F. Hilel, K. Guidara and M.
Gargouri, “NMR Study and Electrical Properties Inves-
tigation of Zn2P2O7,” Ionics, Vol. 16, No. 1, 201
73. doi:10.1007/s11581-00
, 2006, pp. 701-707.
er-
Permittivity and
[28] E. E. Shaisha, Sh. F. El-Desouki, I. Shaltout and A. A.
Bahgat, “Electrical Relaxation in Mixed Alkali Bi2O3-
K2O-Li2O-Fe2O3 Glasses,” Journal of Materials Science
and Technology, Vol. 22
[29] I. Vitioo, “Synthesis, Structure, Conductivity and Ele-
ctrode Properties for Some Double Diphosphates, Sili-
cates and Lithium Manganese Oxides,” Ph.D. Diss
tation, Institute of Solid State Physics, University of
Latvia, Riga, 1999.
[30] Liu J. J., C.-G. Duan, W.-G. Yin, W. N. Mei, R. W.
Smith and J. R. Smith, “Dielectric
Electric Modulus in Bi2Ti4O11,” Journal of Chemical
Physics, Vol. 119, No. 5, 2003, pp. 2812-2819.
doi:10.1063/1.1587685
[31] M. V. N. D. Sharma, A. V. Sarma and R. B. Rao,
asu, “Ac Conductivity and
“Electrical Characterization and Relaxation Behavior of
Lithium-Indium-Phosphate Glasses via Impedance Spec-
troscopy,” Turkish Journal of Physics, Vol. 33, 2009, pp.
87-100.
[32] T. R. Choudhary and A. B
Dielectric Relaxation Studies of Sandstone―A Corre-
lation with Its Thermoluminescence,” Journal of Ovonic
Research, Vol. 4, 2008. pp. 35-42.