Engineering, 2009, 1, 161-166
doi:10.4236/eng.2009.13019 Published Online November 2009 (http://www.scirp.org/journal/eng).
Effect of Low Velocity Impact Damage on Buckling
Properties
Ahmet YAPICI, Mehmet METIN
Mechanical Engineering Department, Mustafa Kemal University, Iskenderun, Turkey
Received January 10, 2009; revised February 21, 2009; accepted February 23, 2009
Abstract
The work described herein consists of experimental measurement of the post-impact buckling loads of E-
glass/epoxy laminates. Composite samples with stacking sequence of [+45/45/90/0]2s were subjected to
low-velocity impact loading at energy levels of 36, 56.13, 79.95, 110.31 and 144 J. The impact tests were
conducted with a specially developed vertical drop weight testing machine. Impact parameters like peak load,
absorbed energy, deflection at peak load and damage area were evaluated and compared. Damaged speci-
mens were subjected to compressive axial forces and buckling loads of the specimens were obtained. The
relation between energy levels and buckling loads is investigated.
Keywords: Low Velocity Impact, E-Glass/Epoxy, Composite, Buckling
1. Introduction
The fiber-reinforced composite plates as used in space
vehicles, aircraft, modern vehicles and light weight
structure are very susceptible to low velocity transverse
impact damage such as matrix cracking, delamination
and fiber breakage [1]. Low velocity impacts which may
occur during manufacture, maintenance and by careless
handling [2] are considered to be dangerous for a com-
posite structure because the damage caused tends to be
created on the back face or within the laminate and hence
is difficult to detect [3,4]. The dynamic response of
composite structures subjected to transient dynamic
loading has been studied in terms of analytical, numeri-
cal [5,6] and experimental works [7–10]. Theoretically,
many works have been developed with an aim of study-
ing the behavior of composite targets under low-velocity
impact.
Previous work with thin, impact damaged composite
laminates [11–14] has shown that an important mecha-
nism of strength reduction is buckling of delaminated
plies. Buckled plies are unable to carry the same propor-
tion of load as unbuckled ones, resulting in a reduced
failure load for the complete laminate [15].
Composite materials normally dissipate a significant
amount of energy by fracture mechanisms such as matrix
cracks, delaminations, fiber fracture, fiber–matrix de-
bonding and fiber pull-out not like more conventional
materials (i.e. metals) where the impact energy is mainly
absorbed by plastic deformation. Delamination is par-
ticularly harmful, since it can seriously degrade the
compressive mechanical properties of the material and
may propagate under subsequent loads leading to the
unexpected failure of the component [16].
In this paper, the results of an experimental study are
presented in which flat E-glass/epoxy laminated panels
are subjected to low velocity impact and then to buckling
force. The relation among energy levels, damage areas
and buckling loads is investigated.
2. Experimental
2.1. Materials and Specimens
In this study unidirectional E-glass/epoxy composite plates
were used. The panels were cut into specimens of 140 x
140 mm in dimension with an average thickness of 3 mm
and stacking sequence of [+45/-45/90/0]2s. The mechani-
cal properties of a lamina are listed in Table 1 [17].
Table 1. Mechanical properties of the single layer.

A. YAPICI ET AL. 162
Figure 1. A schematic of drop tower impact machine.
The square specimens were clamped on all four edges to
provide an impact area of 130 x 130 mm.
2.2. Low-Velocity Impact Testing
The impact equipment was used to conduct the low ve-
locity impact tests. Figure 1 shows the rig used in this
investigation.
Different energy levels can be applied to the clamped
specimen by using the impact machine. This machine has
three main parts; a drop weight tower, a base plate which
holds the specimen and a control unit housing. When the
weight released the cylindrical impactor with a hemi-
spherical head (Figure 2) strikes the specimen, the data is
recorded by the computer.
Figure 2. The weight and the impactor head.
The specimens were firmly fixed at all edges using
clamps and were impacted producing damage up to per-
foration. The total mass, including impactor, load cell,
carriage with linear roller bearings and add-on weights,
was 18 kg. Five different energy levels were used for
each panel configuration 36, 56.13, 79.95, 110.31 and
144 J to obtain 2.0, 2.5, 3.0, 3.5 and 4.0 m/s impact ve-
locities, respectively. A sophisticated instrumentation is
used to record the impact event.
National Instruments (NI) Signal Express data acquisi-
tion software is used to obtain the force and time data
from the force sensor. The acceleration of the weight is
calculated by using Newton’s second law of motion. The
first integration gives the velocity and the second inte-
gration gives the displacement as a function of time. The
equation of motion can easily be integrated imposing
initial conditions (see [9]). Time axis has its origin at the
contact time, while the reference quote h which is at a
fixed, known distance from the upper undeformed sur-
face of the specimen. So, the impactor coordinate is

 00 y at time 0

t. Considering the impactor as a
free falling rigid body, the order of magnitude of its im-
pact velocity at the contact time is obviously given by
hgv  2
0. h

is defined as the height loss of the
gravity center of the impactor mass with respect to the
reference surface. This simple integration can be per-
formed on the acceleration to obtain the velocities and,
then, the coordinate of the impactor. By integration of
the force vs. displacement, the energies time history dur-
C
opyright © 2009 SciRes. ENGINEERING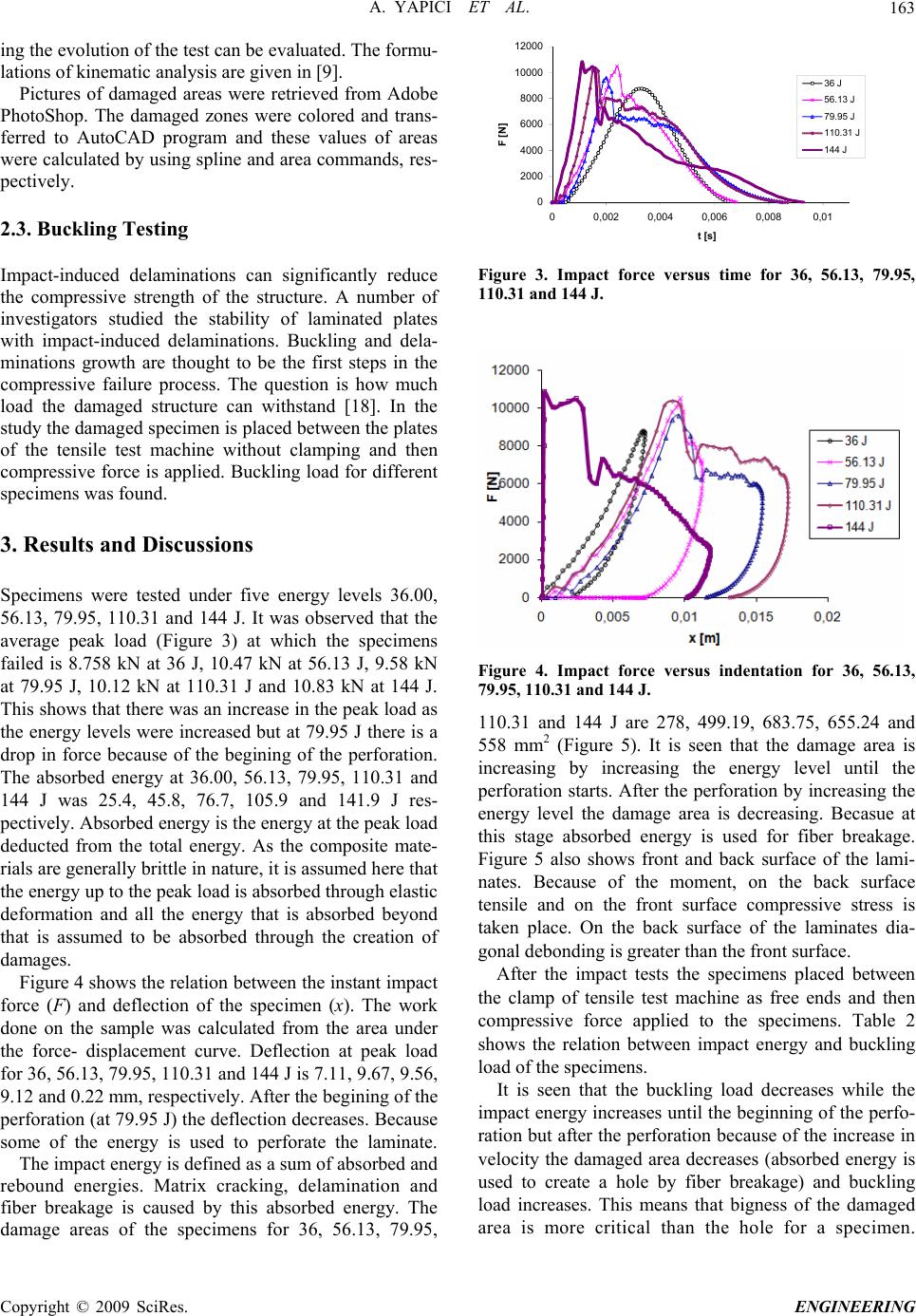

A. YAPICI ET AL.163
ing the evolution of the test can be evaluated. The formu-
lations of kinematic analysis are given in [9].
Pictures of damaged areas were retrieved from Adobe
PhotoShop. The damaged zones were colored and trans-
ferred to AutoCAD program and these values of areas
were calculated by using spline and area commands, res-
pectively.
2.3. Buckling Testing
Impact-induced delaminations can significantly reduce
the compressive strength of the structure. A number of
investigators studied the stability of laminated plates
with impact-induced delaminations. Buckling and dela-
minations growth are thought to be the first steps in the
compressive failure process. The question is how much
load the damaged structure can withstand [18]. In the
study the damaged specimen is placed between the plates
of the tensile test machine without clamping and then
compressive force is applied. Buckling load for different
specimens was found.
3. Results and Discussions
Specimens were tested under five energy levels 36.00,
56.13, 79.95, 110.31 and 144 J. It was observed that the
average peak load (Figure 3) at which the specimens
failed is 8.758 kN at 36 J, 10.47 kN at 56.13 J, 9.58 kN
at 79.95 J, 10.12 kN at 110.31 J and 10.83 kN at 144 J.
This shows that there was an increase in the peak load as
the energy levels were increased but at 79.95 J there is a
drop in force because of the begining of the perforation.
The absorbed energy at 36.00, 56.13, 79.95, 110.31 and
144 J was 25.4, 45.8, 76.7, 105.9 and 141.9 J res-
pectively. Absorbed energy is the energy at the peak load
deducted from the total energy. As the composite mate-
rials are generally brittle in nature, it is assumed here that
the energy up to the peak load is absorbed through elastic
deformation and all the energy that is absorbed beyond
that is assumed to be absorbed through the creation of
damages.
Figure 4 shows the relation between the instant impact
force (F) and deflection of the specimen (x). The work
done on the sample was calculated from the area under
the force- displacement curve. Deflection at peak load
for 36, 56.13, 79.95, 110.31 and 144 J is 7.11, 9.67, 9.56,
9.12 and 0.22 mm, respectively. After the begining of the
perforation (at 79.95 J) the deflection decreases. Because
some of the energy is used to perforate the laminate.
The impact energy is defined as a sum of absorbed and
rebound energies. Matrix cracking, delamination and
fiber breakage is caused by this absorbed energy. The
damage areas of the specimens for 36, 56.13, 79.95,
0
2000
4000
6000
8000
10000
12000
00,002 0,004 0,006 0,0080,01
F [N]
t [s]
36 J
56.13 J
79.95 J
110.31 J
144 J
Figure 3. Impact force versus time for 36, 56.13, 79.95,
110.31 and 144 J.
Figure 4. Impact force versus indentation for 36, 56.13,
79.95, 110.31 and 144 J.
110.31 and 144 J are 278, 499.19, 683.75, 655.24 and
558 mm2 (Figure 5). It is seen that the damage area is
increasing by increasing the energy level until the
perforation starts. After the perforation by increasing the
energy level the damage area is decreasing. Becasue at
this stage absorbed energy is used for fiber breakage.
Figure 5 also shows front and back surface of the lami-
nates. Because of the moment, on the back surface
tensile and on the front surface compressive stress is
taken place. On the back surface of the laminates dia-
gonal debonding is greater than the front surface.
After the impact tests the specimens placed between
the clamp of tensile test machine as free ends and then
compressive force applied to the specimens. Table 2
shows the relation between impact energy and buckling
load of the specimens.
It is seen that the buckling load decreases while the
impact energy increases until the beginning of the perfo-
ration but after the perforation because of the increase in
velocity the damaged area decreases (absorbed energy is
used to create a hole by fiber breakage) and buckling
load increases. This means that bigness of the damaged
area is more critical than the hole for a specimen.

A. YAPICI ET AL 164
(a) Front surface for 36 J.
(b) Back surface for 36 J.
(c) Front surface for 56.13 J.
(d) Back surface for 56.13 J.
(e) Front surface for 79.95 J.
(f) Back surface for 79.95 J.
In other words, sum of matrix cracking, delamination
decreases the buckling strength more than a hole (fiber-
breakage). Also it is seen that 36 J not perforated and
144 J perforated impact energy has the same effect on
buckling properties.
4. Conclusions
The composite plates were subjected to low velocity im-
pact. The relation between the force-time and force-de-
flection was found. It is seen that while the energy
C
opyright © 2009 SciRes. ENGINEERING

A. YAPICI ET AL 165
(g) Front surface for 110.31 J. (h) Back surface for 110.31 J.
(i) Front surface for 144 J.
(j) Back surface for 144 J.
Figure 5. Damage areas of impacted specimen.
Table 2. Buckling load for 36, 56.13, 79.95, 110.31 and 144J.
Impact Energy [J] Buckling Force [kN]
0 13
36 10
56.13 9
Not perforated
79.95 6.5
110.31 8 Perforated
144 10
(impact velocity) increases the peak in force increases
but there is a drop at the beginning of the perforation.
The total energy is used for matrix cracking, delamina-
tion, fiber breakage and elastic energy to make the in-
denter jump (other unimportant energy loss can be ne-
glected). It is seen that when the impact energy increases
the damaged area also increases and buckling load de-
creases until the beginning of the perforation. For 110.31
J, because of the increase in velocity (3.5 m/s), perfora-
tion is occur and the part of the energy, used for matrix
cracking and delamination, is used for fiber breakage
thus the damage area decreases. When the damage area
starts to decrease the buckling load starts to increase after
the perforation.
5. References
[1] R. Tiberkak, M. Bachene, S. Rechak, and B. Necib,
“Damage prediction in composite plates subjected to low
velocity impact,” Composite Structures, Vol. 83, No. 1,
pp. 73–82, 2008.
[2] C. Bert, “Recent advances in dynamics of composite
structures,” Composite Structures IV, Damage Assess
Mater Eval., Vol. 2, pp. 1–17, 1987.
[3] W. Cantwell and J. Morton, “Detection of impact damage
in CFRP laminates,” Composite Structures, Vol. 3, pp.
241–57, 1987.
[4] A. R. Chambers, M. C. Mowlem, and L. Dokos, “Evalu-
ating impact damage in CFRP using fibre optic sensors,”
Composites Science and Technology, Vol. 67, pp. 1235–
1242, 2007.
C
opyright © 2009 SciRes. ENGINEERING

A. YAPICI ET AL. 166
[5] C. F. Li, N. Hu, Y. J. Yin, H. Sekine, and H. Fukunaga,
“Low-velocity impact damage of continuous fiber rein-
forced composite laminates,” Part I, An FEM Numerical
Model, Composites: Part A, Vol. 33, pp. 1055–62, 2002.
[6] C. F. Li, N. Hu, Y. G. Cheng, H. Fukunaga, and H. Se-
kine, “Low-velocity impact-induced damage of continu-
ous fiber-reinforced composite laminates,” Part II Verifi-
cation and Numerical Investigation, Composites: Part A,
33, pp. 1063–72, 2002.
[7] Z. Aslan, R. Karakuzu, and B. Okutan, “The response of
laminated composite plates under low-velocity impact
loading,” Composite Structures, Vol. 59, pp. 119–27,
2003.
[8] F. Mili and B. Necib, “Impact behavior of cross-ply
laminated composite plates under low velocities,” Com-
posite Structures, Vol. 51, pp. 237–44, 2001.
[9] M. Uyaner and M. Kara, “Dynamic Response of Lami-
nated Composites Subjected to Low-velocity Impact,”
Journal of Composite Materials, Vol. 41, No. 24, pp.
2877–2896, 2007.
[10] B. Whittingham, I. H. Marshall, T. Mitrevski, and R.
Jones, “The response of composite structures with
pre-stress subject to low velocity impact damage,” Com-
posite Structures, Vol. 66, pp. 685–698, 2004.
[11] G. Clark, “Modelling of impact damage in composite
laminates,” Composites, Vol. 20, pp. 209–14, 1989.
[12] Y. Xiong, C. Poon, P. V. Straznicky, and H. Vietinghoff,
“A prediction method for the compressive strength of
impact damaged composite laminates,” Composite
Structures, Vol. 30, pp. 357–67, 1995.
[13] M. J. Pavier and M. P. Clarke, “Finite element prediction
of post impact compressive strength in carbon fibre com-
posites,” Composite Structures, Vol. 36, pp. 141–53,
1996.
[14] M. de Freitas and L. Reis, “Failure mechanisms of com-
posite specimens subjected to compression after impact,”
Composite Structures, Vol. 42, pp. 365–73, 1998.
[15] G. J. Short, F. J. Guild, and M. J. Pavier, “Post-impact
compressive strength of curved GFRP laminates,” Com-
posites: Part. A, Vol. 33, pp. 1487–1495, 2002.
[16] F. Aymerich, C. Pani, and P. Priolo, “Effect of stitching
on the low-velocity impact response of [03/903]s graph-
ite/epoxy laminates,” Composites: Part. A, Vol. 38, pp.
1174–1182, 2007.
[17] M. Metin, “The effect of low-velocity impact damage on
buckling behavior of E-glass/epoxy laminated compos-
ites,” M. S. Thesis in Mechanical Engineering, Selcuk
University Konya, Turkey, 2008.
[18] S. Abrate, “Impact on composite structure,” Cambridge
University Press, NY, USA, 1998.