 Engineering, 2009, 1, 151-160 doi:10.4236/eng.2009.13018 Published Online November 2009 (http://www.scirp.org/journal/eng). Copyright © 2009 SciRes. ENGINEERING Heat Distribution in Rectangular Fins Using Efficient Finite Element and Differential Quadrature Methods ShahNor BASRI, M. M. FAKIR, F. MUSTAPHA, D. L. A. MAJID, A. A. JAAFAR Department of Aerospace Engineering, University Putra Malaysia, Putra, Malaysia E-mail: shahnor@eng.upm.edu Received September 2, 2009; revised September 24, 2009; accepted September 28, 2009 Abstract Finite element method (FEM) and differential quadrature method (DQM) are among important numerical techniques used in engineering analyses. Usually elements are sub-divided uniformly in FEM (conventional FEM, CFEM) to obtain temperature distribution behavior in a fin or plate. Hence, extra computational com- plexity is needed to obtain a fair solution with required accuracy. In this paper, non-uniform sub-elements are considered for FEM (efficient FEM, EFEM) solution to reduce the computational complexity. Then this EFEM is applied for the solution of one-dimensional heat transfer problem in a rectangular thin fin. The ob- tained results are compared with CFEM and efficient DQM (EDQM), with non-uniform mesh generation). It is found that the EFEM exhibit more accurate results than CFEM and EDQM showing its potentiality. Keywords: Efficient Finite Element Method, Efficient Differential Quadrature Method, Heat Transfer Problem 1. Introduction Presently there are many numerical solution techniques known to the computational mechanics community. FEM is one of those numerical solution techniques to solve structural, mechanical, heat transfer, and fluid dynamics which arise in problems of engineering and physical sci- ences [1–5]. Here, conventional FEM (CFEM) means the used elements are of same size and uniformly distributed. In its application to the solution of engineering problems, the finite element discretization has been implemented almost to the spatial problems. For dynamic or time de- pendent problems whose solutions as functions of time are of interest, a step by step procedure of finite differ- ence is usually employed with computational complexity. For heat transfer problems, rapid changes of heat/temperature distributions take place near the ele- ment boundary (and at the boundary). It is very impor- tant to know these temperature change behavior of an element prior to its use. Hence, to get an actual picture using FEM, the element is usually subdivided into very small sub-elements uniformly (conventional FEM, CFEM), which leads to huge amount of complexity, memory consumption and computational time [6]. Oth- erwise, error flow occurs with unreliable results [1,2,6]. On the other hand, to get a clear picture about the tem- perature changes near (and at) the element boundary, better to subdivide the elements into very small sub- elements at the boundary only, followed by relatively bigger elements gradually towards the mid-point of the element non-uniformly (efficient FEM, EFEM). This may serve the intended purpose without any additional burden and this is highlighted in this paper with im- proved accuracy (approximately 65%) compared to CFEM. Hence, here, focus is given to develop and apply efficient (non-uniform mesh density) nodal points distri- bution algorithm for automatic mesh (elements) genera- tion to optimize CFEM solution. DQM is another numerical solution technique to solve above mentioned problems efficiently [7–13]. The es- sence of the DQM is that the partial derivative of a func- tion is approximated by a weighted linear sum of the function values at given discrete points. Bellman and Casti [7,8] developed this numerical solution technique in the early 1970s and since then, the technique has been successfully employed in a variety of problems in engi- neering and physical sciences. To make the DQM more efficient with less computational complexity, efficient DQM (EDQM) was proposed in [11–13] with non-uni- formly distributed mesh points. Hence, in this paper, one-dimensional (1-D) heat con- duction problems in a thin rectangular fin are solved us- ing EFEM by means of the accurate discretization and solver (code) and then the results are compared with  S. N. BASRI ET AL. Copyright © 2009 SciRes. ENGINEERING 152 CFEM and EDQM to verify EFEM efficiency. The paper is organized as follows. Section II presents the governing equation with efficient FEM rules, fol- lowed by simulation set-up and assumptions, results and discussions, and finally conclusion of the paper. 2. The One-Dimensional Efficient Finite Element Method Here, the considered one dimensional (1-D) heat conduc- tion problem is [2,3,14–18] 0 ddT kQ dx dx (1) with the boundary conditions 0 0TT x and ( L xL qhTT ) as shown in Figure 1. Here, heat flux dt qk dx . Figure 1 shows the 1-D element discretiza- tion in the x-direction. The temperature at various nodal points are the unknowns except at node 1, where, with initial temperature. Within a typical element ‘ 01 TT 0 T eo ei i x 12e lx ’ the local node numbers are iand with coordinates and and element length, . For example, whose local node num- bers are 1.and 2 with coordinates and , and ele- ment length respectively. 1i 1eii lx i x 1 x 1i x 1 x 1e 2 x An one-dimensional thin rectangular fin as shown in Figure 2 is considered here. Heat is transmitted along its length by conduction and dissipated from its lateral sur- faces to the surroundings by convection. The governing equation for the temperature in the fin is given in Equa- tion (1). The parameter, is given by2 C hp MkA , where, p is the fin perimeter (meter) and Ac is the cross sectional area of the fin [meter2]. Fin length, width and thickness are , and t respectively. Lw In this case, dT qhTT k dx , 2pwt, C wt and 22 C wt p wt t . The convection heat loss in the fin is equivalent to negative heat source and can be expressed as follows: () CC pdxh TTph QT Adx A T Now Equation (1) becomes 0 C ddTph kTT dx dxA (2) Figure 1. Boundary conditions for 1-D heat conduction. Figure 2. Thin rectangular fin. To calculate the approximate solution T, the mathe- matical formulation using Galerkin’s approach [2,3] is 0 0 L C ddTph kTTdx dxdx A (3) where is a test function constructed from the same basis functions as those of T, with . 00 Integrating by parts Equation (3) becomes, 000 0 LLL C dTd dTph kkdx TTdx dxdx dxA (4) The 1st term of Equation (4) is, 0 00 0 L dT dTdT kLkLLk dx dxdx (5) Since 00 and L dT qkL LhTT dx , we get, 0 L L dT kLhT dx T Equation (4) becomes 00 0 LL L C ddT ph LhTTkdxT Tdx dx dxA (6) A global virtual temperature vector is defined as then within each element, th 123 ,,,..., T L  S. N. BASRI ET AL. Copyright © 2009 SciRes. ENGINEERING 153 test function becomes According to Reference [2],e T dT dx BT , we have T d dx B () ii iN (7) Here, is the element shape function and N1 L N at the element boundary [2] (Figure 1). Therefore Equation (7) gives For matrix multiplication validity, we have T TT ei T ddT dx dx T BψBT L LN (8) and 22 11 1 111 11 11 11 111 () () TT ii iiiiei xx xxxxl 11 11 T BB The element conductivity matrix is The element heat rate vector due to the heat source is 1 1 11 11 2 ei eiei TTT ei kl k kd l T BB (9) 1 1 1 1 22 eieiei ei Q Ql Ql d T Rr N (10) where, varies from to 11 and 11 22 ()1 i ii Now, Equation (2) can be transformed into ii xwith ddx xx xx . 11 11 0 22 e ei eiei ei lL TT ei ei kl Ql hT Tdd TT TT ψBB TψN (11) or TLL L hT hT TT ψKT ψR (12) where, global matrices KT , R, and T are respec- tively, T ψ 1112 13 1 2122 23 2 1 3132 33 3 1 122 ... ... ... 2.................................................... ... L L ei ei TTT L ei LLLL KKKK KKKK kl dKK K K KKKK T KBB 212223221 0 22 31323333331 0 41424344441 0 123 10 ... ... ... .. ....................................... . ... L L L LL LL LLLL KK KKT TR KKKT RKT KKKT RKT TRhT KKK hKT (16) L (13) This equation needs to be solved to obtain the 1-D FEM numerical temperature distribution in the consid- ered rectangular fin. 1 123 1 ... 2 ei ei L ei Ql dRRRR T T RN (14) Using Equations (11-16) and the efficient FEM (EFEM) algorithm, the approximate solution T has been obtained. The 1-D EFEM algorithm (rule) is depicted in terms of self-explanatory flow chart in Figure 3. The non-uniform and uniform mesh distribution scenarios are shown in Figures 4 and 5 respectively. 2 3 000...00 000...00 00...00 010... 00 00...00001... 00 ................... ............. ................ .... ................. ............ ................. ...... 000... 01 000...0 L T ψ 2.1. Example Problem 1: 1-D Insulated Tip Thin Rectangular Fin (15) and with constant. 123 ... L TTT TT T10 TT When the base of the fin is held at constant temperature, T0 and the tip of the fin is insulated, the boundary condi- tions are then given by Finally, the global matrix is formed and the Equation (12) becomes 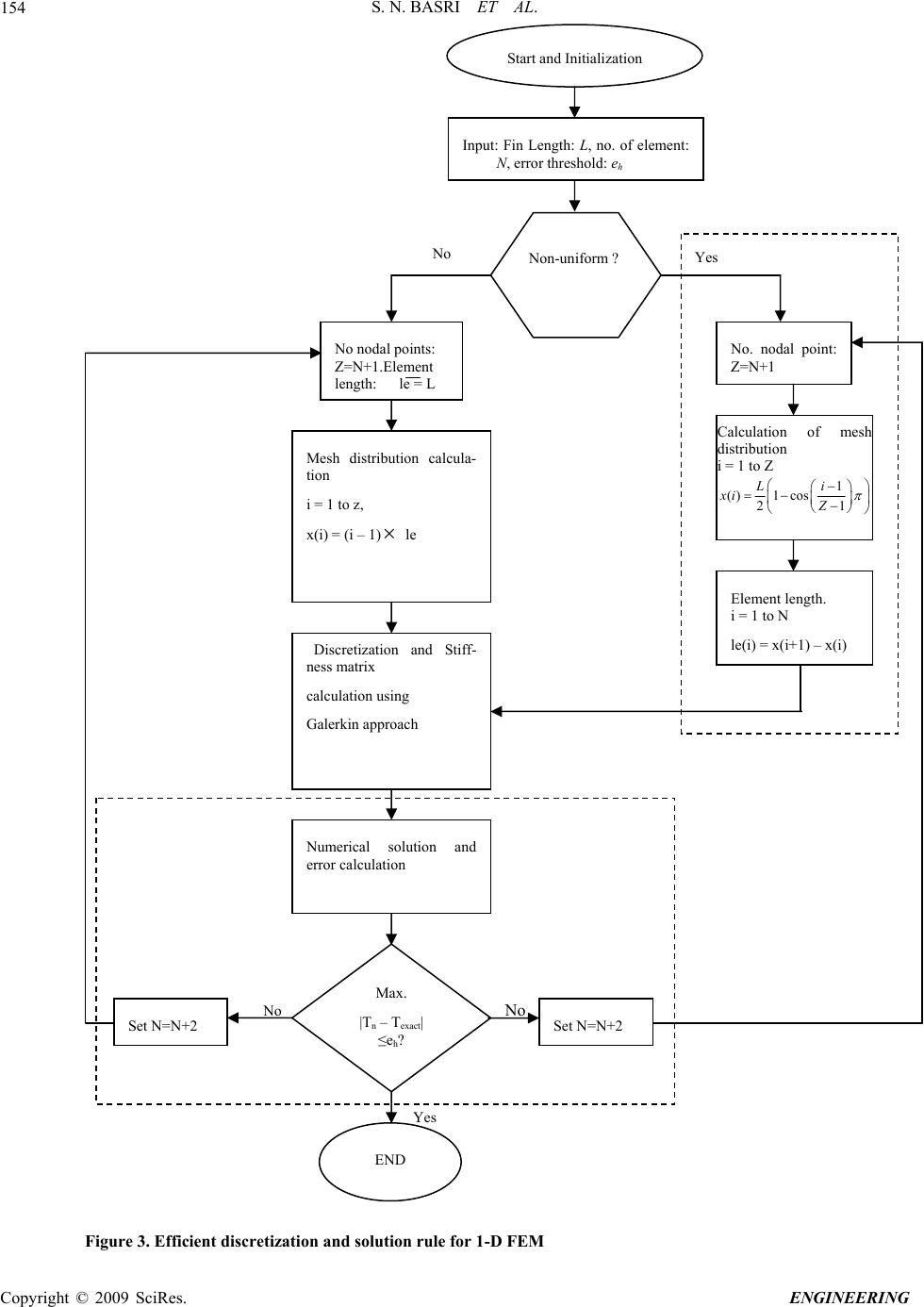 S. N. BASRI ET AL. 154 Start and Initialization Input: Fin Length: L, no. of element: N, error threshold: eh Figure 3. Efficient discretization and solution rule for 1-D FEM No Yes No No Yes No. nodal point: Z=N+1 Calculation of mesh distribution i = 1 to Z 1 ()1 cos 21 Li xi Z Element length. i = 1 to N le(i) = x(i+1) – x(i) Non-uniform ? No nodal points: Z=N+1.Element len th: le = L Mesh distribution calcula- tion i = 1 to z, x(i) = (i – 1) le Numerical solution and error calculation Max. |Tn – Texact| ≤eh? Set N=N+2 Discretization and Stiff- ness matrix calculation using Galerkin approach Set N=N+2 END C opyright © 2009 SciRes. ENGINEERING  S. N. BASRI ET AL. 155 0 TT at 0x 0q at L, where L is the length of the fin. In this case, the final form of the global matrix in Equation (16) becomes 2223221 0 22 323333331 0 23 1 ... ... ......... ............ ... L L LL LLLLL = L = 0 x x = L x = 0 0 AAA TR T AATRAT AATRA T 0 (17) Example of non-uniform and uniform mesh distribu- tions and element lengths are depicted in Figures 4 and 5 respectively. 2.2. Example Problem 2: 1-D Convection Tip Thin Rectangular Fin When the base of the fin is held at a constant temperature, T0 and the tip of the fin is a convection surface, then the boundary conditions are T=T0 at x=0 L qhT T at x=L And the final global matrix shown in Equation (16) becomes 2223221 0 22 323333331 0 23 1 ... ... ......... ............ ... L L LL LLLLL AA AAT TR AAA TRAT AA AhTRhTAT (18) 3. Simulation Set-up and Assumptions Table 1 shows the considered parameters and their cor- responding values used to obtain simulation results using FORTRAN 90 software. We used these values to obtain the temperature distribution for EFEM, CFEM, EDQM and exact methods. Figure 4: Example 1-D efficient mesh distribution and ele- ment lengths. Figure 5. Example 1-D conventional mesh distribution and element lengths. We considered, 21 hP MkA and the associated assump- tions (in Table 1) to compare the obtained FEM results with DQM [13] and exact solution [18]. Here to mention that, to obtain 1-D DQM solutions, element material properties, fin-width and fin-thickness are not required (which is the shortcoming of the method). The errors in FEM and DQM solutions are computed compared to exact solution [18]. 4. Results and Discussions 4.1. Results and Discussions of 1-D Insulated Tip Thin Rectangular Fin The results of the present problem, shown in Figure 6, contain the maximum absolute percentage errors in the FEM and DQM solutions obtained with uniformly (con- ventional) and non-uniformly (efficient) distributed no- dal (mesh) points. It is essential to know, how many mesh points (elements) are required to obtain a conver- gent FEM solution in the solution domain. Hence, the comparison of convergence of fin-tem- perature in terms of maximum % error versus number of nodal (mesh) points for CFEM, EFEM and EDQM solu- tions is shown in Figure 6. Initially, all the solutions in terms of maximum % errors show a monotonic conver- gence with the increasing number of mesh points (shown 11to 104Z ). It is apparent that EFEM results show bit less accuracy for 30Z and similar accuracy for compared to EDQM, but yields result with higher accuracy, of one order of magnitude or more with in- creasing 30Z compared to CFEM. EDQM converge up to 100Z and then saturated, whereas the EFEM solutions converge smoothly for all N within the solution domain, showing best converging result at . On the other hand, uniform FEM (CFEM) results converge slowly throughout the solution domain and then diverge without showing the best results like EFEM. It happens due to the mesh point distribution strategy of equally spaced and unequally spaced nodal points in the compu- tational domain and the inherited complexity to compute the stiffness matrix for equally spaced nodal points. Hence, the efficiency of EFEM results is apparent. 100and 101Z Figure 7 shows the convergent numerical and exact solutions (fin temperature) and the corresponding per- centage errors for 100N elements (FEM case) which is equivalent to 101Z mesh points (both FEM and DQM cases). These results are obtained at an interval of 0.1x along the fin length,01 , using cubic C opyright © 2009 SciRes. ENGINEERING  S. N. BASRI ET AL. 156 Table 1. Input parameters and assumptions for 1-d rectangular fin. spline interpolation. It is seen that all the solutions are very close to exact solutions throughout the length of the fin with temperature variations at 0 01TC0 m to at 0 0.648 L TC1.0 m. Figure 8 shows the percentage errors at the base of the fin () are 0 for all solutions due to initial tempera- ture (Figure 7). The percentages errors remain the same with EFEM except little bit increase (with maximum error) at the middle of the fin due to nodal point distribution with maximum spacing there. Whereas, with CFEM, it increases gradually along the length of the fin with the maximum percentage error at the fin-tip (x = 1). In other case, the oscilla- tions (instability) of DQM results appear clearly com- pared to FEM results. The average percentage error in 0x 01T 4 10 0C 6 2.44 10 1.9 CFEM, EDQM [13] and EFEM are4 1.2 10 , and respectively, which shows approximately 99% and 49% improvements in EFEM results demonstrating its superiority over CFEM and EDQM. 6 2.24 10 6 1.12 10 4.2. Results and Discussion of 1-D Convection Tip Thin Rectangular Fin Here the results exhibit the same nature like insulated-tip fin but yield results with higher accuracy, of two order of magnitude or more with increasing due to different material properties and fin-thickness (as the FEM solu- tion and its accuracy depend on fin dimension, materials used and associated boundary conditions). In Figure 9, the comparison of convergence versus number of mesh points of exact, FEM and DQM solu- tions for convection-tip fin with uniform and non-uni- form mesh distributions is shown. It is apparent that for all cases, the solutions converge smoothly for all within the solution domain. The comparison shows similar results as in Figure 6 except EFEM yields result with higher accuracy, of one order of magnitude or more with increasing (for ) compared to that with CFEM. Here, EFEM results converge from 20Z 80Z showing best result at90to 101Z , EDQM [13] shows similar results with some oscillations, whereas CFEM does not exhibit any best convergence. Input Parameters Assumed value for Insulated-Tip Fin Assumed value for Convec- tion-Tip Fin Boundary and other values: Initial temperature (T0) Ambient temperature (T∞) Heat flux (q) % Error threshold (eh) 1 OC 0 OC 0 at x = 1 0 - 0.1 1 OC 0 OC Variable 0 - 0.1 Element Type (NNODE): Linear (for 1-D) 2 2 Element material properties: Thermal conductivity (ke = k) Convective heat transfer coefficient (h) Heat source (Q) Variable to make M = 1 9 W/m2 0C 0 W/m3 0C 7.03125 W/(m 0C) 9 W/m2 0C 0 W/m3 0C Element (Fin) dimension: length (L) along x-axis width (w) thickness (t) Number of elements (N) 1 m Variable to make M = 1 0.001 m 11 - 104 1 m Variable to make M = 1 Variable to make M = 1 11 - 104 C opyright © 2009 SciRes. ENGINEERING  S. N. BASRI ET AL. 157 Figure 6. Comparison of convergence of insulated-tip fin-temperature in terms of maximum % error for CFEM, EFEM and EDQM solutions (). 11to 104Z Figure 7. Insulated-tip fin-temperature distribution for exact, EFEM, CFEM and EDQM along with its respective % errors (). Z=101 Figure 10 depict the comparison of CFEM, EFEM, EDQM [13] numerical and exact convection-tip fin tem- peratures and the corresponding percentage errors for conventional (uniform) and efficient (non-uniform) mesh point distribution respectively for 100 elements (i.e., ). Same as Insulated-tip fin, the results are ob- tained at an interval of along the fin length, 101Z 0 0.1x 1 , using cubic spline interpolation. Figure 10 shows that, all numerical solutions are very close to ex- act solutions throughout the length of the fin with tem- perature variations 0at base of the fin to at the tip of the fin. Here the reduction of fin temperature is more compared to insu- lated-tip fin (Figure 7) as expected. 0 1T 0 0.32 C C C 0 0.328 L T FEM versus DQM maximum % error comparison for convection-tip fin-temperature are shown in Figure 11. The comparison of CFEM, EFEM and EDQM [13] per- C opyright © 2009 SciRes. ENGINEERING 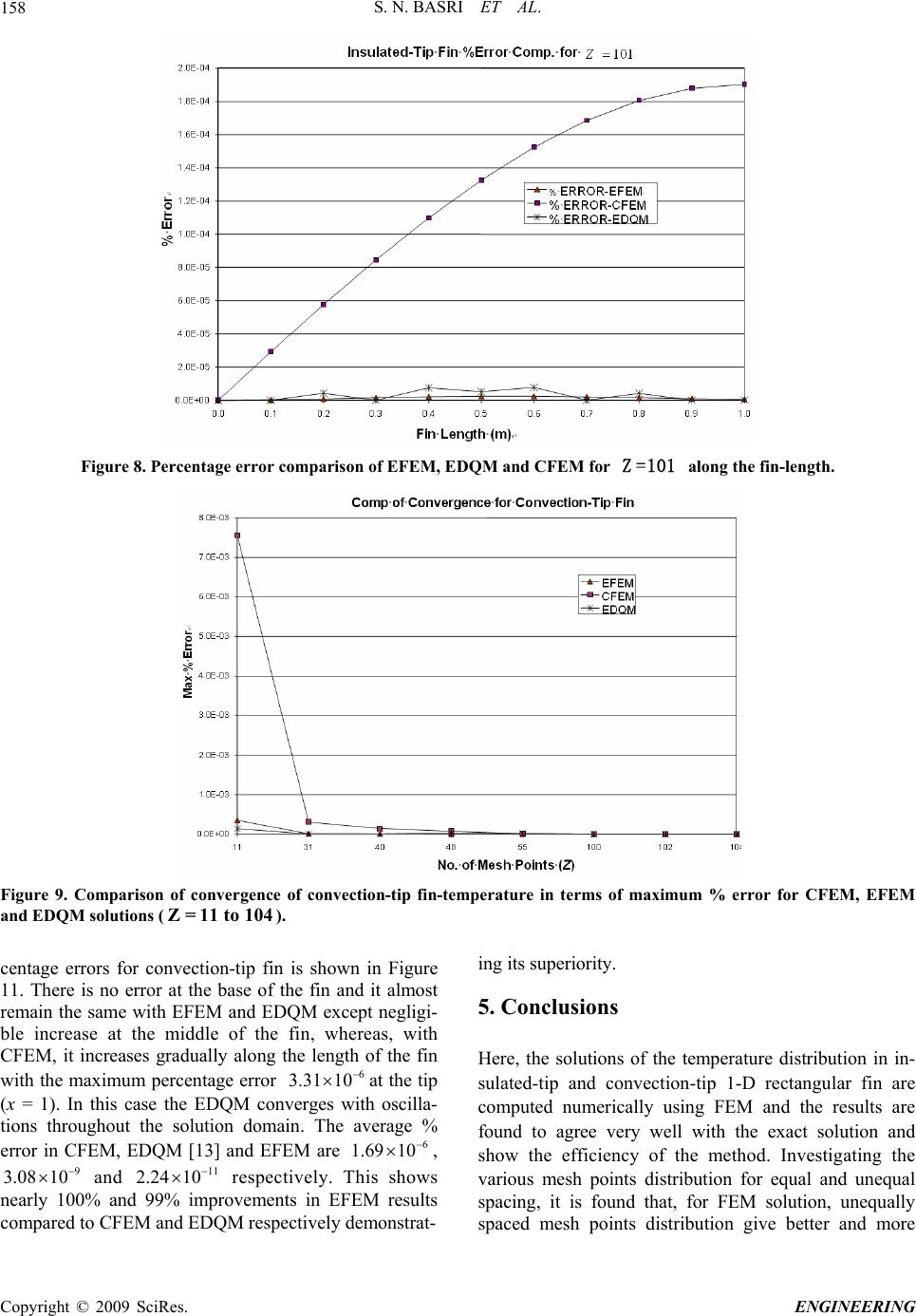 S. N. BASRI ET AL. 158 Figure 8. Percentage error comparison of EFEM, EDQM and CFEM for along the fin-length. Z=101 Figure 9. Comparison of convergence of convection-tip fin-temperature in terms of maximum % error for CFEM, EFEM and EDQM solutions (). Z=11to 104 centage errors for convection-tip fin is shown in Figure 11. There is no error at the base of the fin and it almost remain the same with EFEM and EDQM except negligi- ble increase at the middle of the fin, whereas, with CFEM, it increases gradually along the length of the fin with the maximum percentage error at the tip (x = 1). In this case the EDQM converges with oscilla- tions throughout the solution domain. The average % error in CFEM, EDQM [13] and EFEM are 6 3.31 10 1.69 6 10 , and respectively. This shows nearly 100% and 99% improvements in EFEM results 9 3.08 10 11 2.24 10 compared to CFEM and EDQM respectively demonstrat- ing its superiority. 5. Conclusions Here, the solutions of the temperature distribution in in- sulated-tip and convection-tip 1-D rectangular fin are computed numerically using FEM and the results are found to agree very well with the exact solution and show the efficiency of the method. Investigating the various mesh points distribution for equal and unequal spacing, it is found that, for FEM solution, unequally spaced mesh points distribution give better and more C opyright © 2009 SciRes. ENGINEERING  S. N. BASRI ET AL. 159 Figure 10. Convection-tip fin-temperature distribution for exact, EFEM, CFEM and EDQM along with its respective % er- rors (Z). =101 Figure 11. Convection-tip fin error comparison of EFEM, EDQM and CFEM for along the fin-length. Z=101 accurate results than equally spaced and the solution converges smoothly as the number of nodal points (or elements) is increased. In general, this study has im- proved the stability and accuracy of EFEM results for practical consideration and implementation. Finally, the results of EFEM shows remarkable en- hancement compared to CFEM and agree very well with EDQM with very small errors or difference showing its potentiality. Hence EFEM is suitable to test the tem- perature distribution scenario in any thin metal fin prior to its design and practical implementation. 7. References [1] G. Strang and G. J. Fix, “An analysis of the finite element method,” Prentice-Hall, Inc., 1997. [2] R. Tirupathi and P. E. Chandrupatla, Introduction to finite elements in engineering, Prentice-Hall International, 1997. [3] “Mathematics of finite element method,” 2004, Available at: http://math.nist.gov/mcsd/savg/tutorial/ansys/FEM/ (Accessed on October 19, 2006). [4] B. Li, “Numerical method for a parabolic stochastic partial differential equation,” Chalmers Finite Element Center, 2004. C opyright © 2009 SciRes. ENGINEERING  S. N. BASRI ET AL. Copyright © 2009 SciRes. ENGINEERING 160 [5] F. Fairag, “Numerical computations of viscous, incom- pressible flow problems using a two-level finite element method,” arXiv: Math.NA/0109109, Vol. 1, No. 17, Sep- tember 2001. [6] S. Park, “Development and applications of finite elements in time domain,” PhD Thesis, Faculty of the Virginia Polytechnic Institute and State University, Virginia, De- cember, 1996, Available in the Library, Virginia Poly- technic Institute and State University. [7] R. Bellman and J. Casti, “Differential quadrature and long-term integration,” J Math and Appl., Vol. 34, pp. 235–238, 1971. [8] R. Bellman and J. Casti, “Differential quadrature: A tech- nique for the rapid solution of nonlinear partial differen- tial equations,” J. Comput Phys, Vol. 10, pp. 40–52, 1972. [9] C. W. Bert, S. K. Jang, and A. G. Striz, “Nonlinear bend- ing analysis of orthotropic rectangular plates by the method of differential quadrature,” J. Comput Mech, Vol. 5, pp. 217–226, 1989. [10] C. W. Bert and M. Malik, “Fast computing technique for the transient response of gas-lubricated journal bearings,” Proceedings of the U.S. National Congress of Applied Mechanics, Seattle, WA, pp. 298, June 26-July 1, 1994. [11] C. Shu, W. Chen, H. Xue, and H. Du, “Numerical analy- sis of grid distribution effect on the accuracy of differen- tial quadrature analysis of beams and plates by error es- timation of derivative approximation,” Int. Journal of Numer, Methods Engineering, Vol. 51, No. 2, pp. 159–179, 2001. [12] M. M. Fakir, M. K. Mawlood, W. Asrar, S. Basri, and A. A. Omar, “Triangular fin temperature distribution by the method of differential quadrature,” Journal Mekanikal, Malaysia, Vol. 15, pp. 20–31, 2003. [13] M. M. Fakir, M. K. Mawlood, W. Asrar, S. Basri, and A. A. Omar, “Rectangular fin temperature distribution by the method of differential quadrature,” The Journal of the In- stitute of Engineers, Malaysia (IEM), Vol. 63, No. 4, pp. 41–47, 2002. [14] E. Hinton and D. R. J. Owen, “An introduction to finite element computations,” Pineridge Press Limited, Swan- sea, U.K., 1985. [15] S. Tiwari, G. Biswas, P. L. N. Prasad, and S. Basu, “Nu- merical prediction of flow and heat transfer in a rectan- gular channel with a built-in circular tube,” ASME Jour- nal of Heat Transfer, Vol. 125, No. 3, pp. 413–421, 2003. [16] B. L. Wang, and Z. H. Tian, “Application of finite ele- ment-finite difference method to the determination of transient temperature field in functionally graded materi- als,” Journal of Finite Elements in Analysis and Design, Vol. 41, pp. 335–349, 2005. [17] S. H. Lo and W. X. Wang, “Finite element mesh genera- tion over intersecting curved surfaces by tracing of neighbours,” Journal of Finite Elements in Analysis and Design, Vol. 41, pp. 351–370, 2005. [18] M. N. Ozisik, “Heat transfer: A basic approach,” McGraw-Hill, 1985.
|