Journal of Applied Mathematics and Physics
Vol.06 No.09(2018), Article ID:87141,23 pages
10.4236/jamp.2018.69154
Study on the Maximum Volume of Inscribed Elliptical Cone inside a Cylinder
Yusi Niu, Liyuan Li
The High School Affiliated to the Renmin University of China, Beijing, China




Received: July 30, 2018; Accepted: August 31, 2018; Published: September 7, 2018
ABSTRACT
The volume of a cone is one third of the volume of a cylinder if they share same base and equal height. Let’s propose a hypothesis, if we expand the research area from cones to elliptical cones, could the maximum ratio of volume beyond one third? This paper tries to pull away the veils of it. Firstly, we present four types of inscribed elliptical cones inside cylinders, and consequently all the other inscribed elliptical cones can be classified to these four types. Secondly, for each type of them, this paper discusses the corresponding volume ratio of the inscribed elliptical cone to the cylinder. It is concluded that the largest ratio of the volume of an inscribed cone to that of the cylinder is 1/3. Finally, two types whose ratio could reach 1/3 are given as examples.
Keywords:
Inscribed Elliptical Cone, Cylinder, Ratio of Volume

1. Introduction
Past learning tells us that the volume of a cylinder is three times that of the cone which shares same base and equal height with the cylinder. In turn, any cone is a third part of the cylinder which has the same base with it and equal height. However, this is the simplest case. This paper extends inscribed cones to inscribed elliptical cones, under the condition of a fixed cylinder, to study and solve the volume of various types of inscribed elliptical cones, and determine which type of inscribed elliptical cones has the largest volume and if the maximum value is more than one third or not. In order to define the scope of the elliptic cones in this paper, we firstly provides the definition of inscribed elliptical cones:
Definition of inscribed elliptical cones: If the bottom base of a cone is inscribed in a cylinder, and the vertex is just on the surface of the cylinder, then we call this cone an inscribed elliptical cone.
Ordinary cones can be regarded as a special case of inscribed elliptical cones.
2. Types of Inscribed Elliptical Cone
Under the condition of a determined cylinder, we divide all kinds of inscribed ellipse cones into the following four types:
Type I
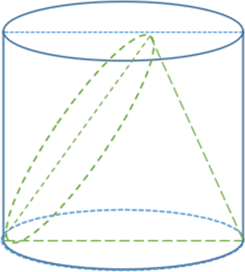
Beginning with the simplest case, Figure 1 shows a cone and a cylinder in same base and equal height.
Type II
The inscribed elliptical cone is placed horizontally in the cylinder, and the intersection of the bottom surface of the elliptical cone and the bottom of the cylinder is parallel to the height of the cylinder, moreover, the vertex of the elliptical cone falls on the side of the cylinder, shown as Figure 2.
Figure 1. The cone.
Figure 2. The cone.
Type III
The third type is that the inscribed cone is tilted into the cylinder. As Figure 3 shows, the cone meets the cylinder at point C, M and N where C is a point on the top surface, M is a boundary point of the bottom surface and N is the vertex which may fall on the side or the bottom of the cylinder. In this case, it is necessary to discuss the cases based on the ratio of the height H of the cylinder to the bottom radius R.
Type IV
The upper and lower two intersection points which contact the bottom of the cone and the cylinder are on the side and bottom surfaces of the cylinder, respectively. In addition, both of the intersection points are movable and the vertex may fall on the side of the cylinder, as well as falls on the bottom of the cylinder. See Figure 4.
Other types of inscribed ellipse cone can be attributed to the above four cases to discuss.
Figure 3. The cone.
Figure 4. The cone.
3. Preliminary Knowledge
Lemma 1: Ellipse Area Theorem
The area of an ellipse is given by:
where a and b are the semi-major and semi-minor axes of the ellipse.
Proof:
The standard equation for an ellipse centered at the origin is given by:
D is the region which is bounded by the ellipse and axes in first quadrant. Noting the symmetry in the ellipses, the entire area equals to the area of D multiplied by 4, therefore [1]
Let:
Which finally goes to:
Lemma 2: Elliptic Cone Volume Theorem
The volume formula of an elliptical cone is:
where h is the height, and a and b are the semi-major and semi-minor axes of the elliptical base.
Proof:
The standard equation for the base of an elliptic cone can be given by: , and h is the height. The semi-major and semi-minor axes of the
elliptic cross with height y are respectively. According to the similar relationships,
Then the volume of an elliptical cone is:
4. Solution of the Volume of the Inscribed Elliptical Cone
In this section, we solve the four types of inscribed elliptical volumes. For convenience, we convert the exact volume of the inscribed elliptical cone into the ratio to the cylinder.
Type I
Beginning with the simplest case, Figure 5 shows a cone and a cylinder in same base and equal height. S is the area of base, H is the height, R is the radius, moreover, a and b are the semi-major and semi-minor axes of the elliptical base.
By Lemma 2, it’s easy to know that Vc = 1/3πR²H, because a = b = R. Thus,
Hence the ratio of volume is 1/3.
Type II
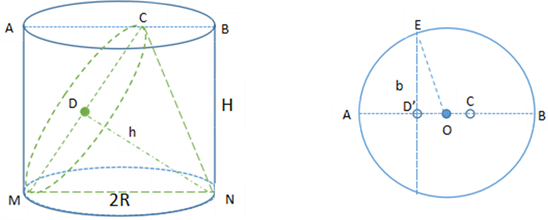
The cone is placed horizontally inside the cylinder, as shown in Figure 6, two intersection points to the upper and lower base are C, D, respectively, and the contact points to the side of cylinder are E, F, respectively. The figure of circle O is the aerial view of Figure 6.
For easier calculation, we set the directions of line CD and EF, respectively, as the directions of semi-major axis a and semi-minor axis b (The same as in the following cases). Because of the variety of the relationship between the height of the cylinder and the radius of the bottom base, it’s possible that a < b, but this will not affect the volume of the elliptic cone.
Now assuming that OC = x, H is the height, R is the radius, then we give the expression:
a = H/2, , h = R + x
According to the Lemma 2,
Figure 5. The cone.
Figure 6. The cone.
Mark the volume ratio of the inscribed elliptical cone to the cylinder as T, then
Since , setting .
Therefore,
Differentiate to get:
When T' = 0, which is the same as , T achieves the maximum by the definition of derivatives.
One can draw a conclusion that an inscribed cone gets largest volume when point C is exactly the middle point of segment OA, and the ration is , which is still less than 1/3.
Type III
In the third type, the lower intersection point of the inscribed elliptical cone and the cylinder is fixed on the point M, which is located on the circumference of the cylindrical bottom. The upper intersection point C is located on the top of the cylinder. The value scope of point C is from point A of the diameter AB to the other point B (shown in Figure 7). When the position of point C is changing, the vertex N of the cone could locate on the surface of the side, could also locate on the cylindrical bottom. Moreover, the ratio of the H and R also has an effect on the location of vertex N.
Based on the analysis, the following conclusions can be drawn: if ,when point C moves from point A towards to point B, the vertex of elliptical cone is located at the surface of the side all along; if , when point C moves from point A towards to point B, the vertex moves from the side surface to the bottom. The following discussion is based on those two scenarios.
Case 1:
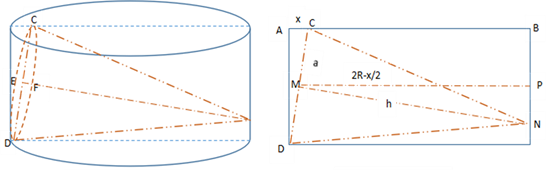
The type of the cylinder is slender, which shown in Figure 8. Assume AC = x, the vertex of the cone is located at point on the side surface, point D is the center point of the bottom of the elliptical cone.
The front view of Figure 8 is shown on the right. In the front view, the point D is the midpoint of line CM, line DF is a parallel line of line AC and perpendicularly intersected at point F. The direction of MC has marked as major axis as normal, and the other direction will be marked as minor axis.
Since ∆AMC ∽ ∆FDE, therefore, , then
Hence, .
In addition,
By the Lemma 2:
Mark the volume ratio of the inscribed elliptical cone to the cylinder as T:
Since the difficulty of directly solving the maximum value of this equation. Hence, the variable substitution and the scaling method are chosen to solve the maximum value.
As , let , then
As , then , when , , so:
Let function , after derivation, we have,
Therefore, the function P(t) is monotonically decreasing on the interval (0,1/3), monotonic increasing on the interval [1/3, 1], In comparison of the value of function P(t) at 0 and 1, the maximum value can be obtained that is the P(1) = 1/3, so
The criteria of this equality is:
When , the volume ratio of the inscribed elliptical cone to the cylinder is less than or equal to .
Case 2: H < 2R
In this case, the cylinder is considered as a short and thick type. The two stages need to be considered at this moment:
Stage one: At the outset of the vertex of the inscribed elliptical cone located at the midpoint of the surface of the cylinder side, until the vertex of the inner elliptical cone located right on the circumference of the cylindrical bottom. A moment of graphics in the first stage as shown in Figure 9, and Figure 10 is the ending position.
Stage two: At the outset of the vertex of the inscribed elliptical cone located right on the circumference of cylindrical bottom and end at x = 2R. A moment of graphics in the Second stage as shown in Figure 11, and Figure 12 is the ending position.
In the first stage,the right triangle CMN in the front view of Figure 10, according to the Pythagorean Theorem:
So,
The front view of Figure 9, assume AC = x,
As ∆ADC ∽ ∆PMN, thus , then ,
Also as
By the Lemma 2:
Assume the volume ratio of the ellipsoid to cylinder is T, then
As , let , then
Mark the right side of the inequality as function , as , obviously . In order to solve the maximum value of the function , we take the derivative of the function , so:
When , ; when , . Therefore, the function is initially increasing, but turns to decrease after. Since , so the maximum value of function is .
When , that is , thus the maximum volume ratio of the cone is
The equality doesn’t hold actually, which means the sign of the less than is strictly true. When H < 2R, at the first stage, the maximum volume ratio of the inner elliptical cone is less than 1/3.
Let research the maximum volume ratio of the inscribed elliptical cone in the second stage, at present, , as shown in Figure 11.
Assume AG = x,as △ADG∽△MND,thus ,
Rearrange to get:
Since
By the Lemma 2:
Assume the volume ratio of the ellipsoid to cylinder is T, then
Since , so:
Mark the right side as function , Again in order to solve the maximum value of the function , we take the derivative of the function , so:
Since (according to the calculation or Figure 3 (3-1)), thus, the function is initially increasing, but turns to decrease after, the maximum of function is , so:
When the cone is in the stage as shown in Figure 12, the maximum volume ratio is achieved, but still less than 1/3, that means the maximum volume ratio of the inscribed elliptical cone to the cylinder in the second stage is less than 1/3.
Summarizing, when H < 2R, the maximum volume ratio of the inner elliptical cone to the cylinder is strictly less than1/3.
Type IV
The point D and point C are the intersection points of the bottom surface of the inscribed elliptical cone and the upper and lower base of the cylinder, respectively. Furthermore, them two are removable, the vertex could locate right on the side of the cylinder, also could locate right on the bottom of the cylinder. It can be considered in two cases: H ≥ 2R and H < 2R.
Case 1: H ≥ 2R
1) The vertex of the inscribed elliptical cone falls on the circumference of the cylindrical bottom.
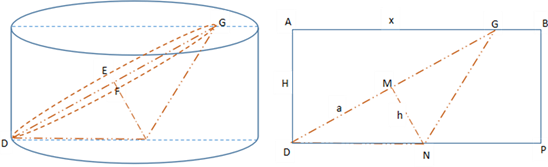
Firstly consider the critical situations: the vertex of the inscribed cone is on the boundary of the bottom surface, as shown in Figure 13.
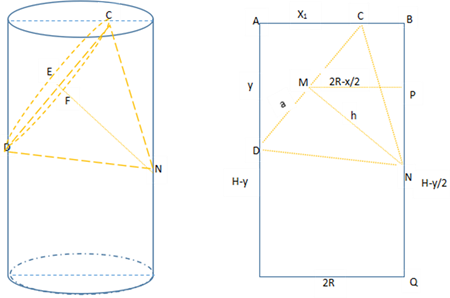
According to the front view of Figure 13, AC = x, AD = y, CD = 2a, MN = h, MP = 2R - x/2, PN = H - y/2. Let’s take just the CD to be the axis of the elliptical bottom base so that the semi-major axis , and the semi-minor axis , which lasts same as before.
Because ∆ADC ∽ ∆PMN, consequently.
Rearrange to get:
As , thus .
Therefore,
, now . That is the relationship between x and y when the vertex of the inscribed elliptical cone falls right on the point N.
Furthermore, due to and H ≥ 2R, it’s concluded that
, which can also be proved by the geometric theory based on Figure 13. Thus, the volume ratio of the inscribed elliptical cone to the cylinder is:
Mark the function , in order to research the maximum of N(x), we calculate its derivative:
Thus, N(x) is monotone increasing, i.e. , also . Therefore:
and the equal sign holds when .
Conclusion: when , if he vertex of the inscribed elliptical cone is exact on the point N, then the volume of the cone is less than or equal to one third the volume of the cylinder, and the solely criteria holds the equal sign is that .
2) The vertex of the inner elliptical cone falls on the side of the cylinder
Figure 14 shows the situation when the vertex of the inner elliptical cone falls on the side of the cylinder. And at the front view of Figure 14, AC = x1, AD = y, ACD = 2a, A MN = h, A MP = 2R − x1/2.
Since ∆ADC ∽ ∆PMN, thus , i.e. .
In addition, .
Then, calculate the volume ratio of the inscribed elliptical cone to the culinder by the Lemma 2:
In order to ensure that the vertex of the inscribed elliptical cone falls on the side of the cylinder, letting .
To check the variation of with y, we calculate the partial derivative of by y:
When , ; When , . Therefore, will decrease first and then increase with the increase of y. Thus we get:
When is at its maximum, which can be classified as the first situation when H ≥ 2R in this type, which is that the vertex falls on the circumference of the bottom of the cylinder, so, when , get its maximum 1/3.
When T(x1, H) is at its maximum, which can be classified as the first situation of type III that is when H ≥ 2. Now the volume ratio of the inscribed cone to the cylinder is less than or equal to one third, and the equal sign holds when H = 2R, x = 2R.
In summary, in type IV, when H ≥ 2R, if the vertex of the inscribed elliptical cone falls on the side of the cylinder, the ratio of the volume of the cylinder is less than or equal to 1/3, and the equal sign holds when: , .
3) The vertex of the inscribed elliptical cone falls on the bottom of the cylinder.
Figure 15 shows the situation when the vertex of the inscribed elliptical cone falls on the bottom of the cylinder, at the front view of Figure 15, AC = x, AD = y, CD = 2a, MN = h, MP = H − y/2.
Known that ∆ADC ∽ ∆PNM, since , i.e. .
Furthermore, as ,
According to the Lemma 2, the ratio of the volume of the elliptical cone to the volume of the cylinder is:
Setting , in order to study the variation of
with the change of x, we calculate the partial derivative of with x:
When the vertex falls on the bottom, , thus , i.e. the variable x is monotone increasing, therefore:
In order to study the variation of with the change of y, calculate the partial derivative of with y:
Set , then .
When , hence the function is monotone decreasing; when , hence the function is monotone increasing.
Set , where y2 solves the equation when .
Since the range of y is , therefore, it’s necessary to study the relationship between .
If , then is monotone decreasing when and monotone increasing when . Therefore the fiction is initially increasing, but turns to decrease after, and the maximum is .
If , then is monotone decreasing and the maximum is .
Summarizing: the maximum of is .
As , which finally goes to .
And the equal sign holds when x = 2R, y = 0 ( are included in the case when the vertex falls on the circumference of the bottom surface of the cylinder.)
When ,in summary of a, b and c, the ratio of the inscribed elliptical cone’s volume to the volume of the cylinder is less than or equal to one third , and the equal sign holds when .
Case 2: H < 2R
1) The vertex exactly falls on the circumference of the bottom of the cylinder
As shown in Figure 16:
In the front view of Figure 16, AC = x, AD = y, CD = 2a, MN = h, MP = 2R − x/2, PN = H − y/2. Let’s take just the CD to be the axis of the elliptical bottom base so that the semi-major axis , and the semi-minor axis , which lasts same as before.
Since ∆ADC ∽ PMN, thus .
Rearrange to get:
As , thus .
Therefore, (now ). Again as , we finally get . That is the relationship
between x and y when the vertex of the inscribed elliptical cone falls right on the point N.
Summarizing: If the vertex falls on the bottom circle, then .
The volume ratio of the inscribed elliptical cone to the cylinder is:
In order to study the variation of with the change of y, we calculate its partial derivative of y:
As
, i.e.
, thus
. Hence the function T(x, y) increases as y increases. As a result, 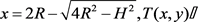 reach the maximum when
.
reach the maximum when
.
Therefore, when H < 2R and the vertex of the inscribed elliptical cone falls just on the bottom of the cylinder, the ratio of the volume is less than 1/3.
1) The vertex falls on the side of the cylinder
Figure 17 shows the situation when the vertex falls on the side of the cylinder.
In the front view of Figure 17, AC = x1, AD = y, CD = 2a, MN = h, DF = 2R − x1/2.
Since ∆ADC ∽ ∆PMN, thus , i.e. ,
According to the Lemma 2, the volume ration of the elliptical cone to the cylinder is:
Calculate the partial derivative of with y
As , i.e. , thus is the criteria of maximum.
Hence, when H < 2, y = H, the volume ratio reaches its maximum, i.e. .
And this situation can be classified in the discussion when H<2R, thus:
In summary, when the vertex of the elliptical cone falls on the side of the cylinder, the maximum ratio of the cone to the volume of the cylinder is less than one third.
2) The vertex falls on the bottom surface of the cylinder
In this case, we discuss and , separately.
Case (1): when
Figure 18 shows the situation when the vertex falls on the bottom of the cylinder, in the front view of Figure 18, AC = x, AD = y, CD = 2a, MN = h, MP = H − y/2.
Since ∆ADC ∽ ∆PNM, thus , i.e. .
Again by and the Lemma 2, the volume ration of the cone to the cylinder is:
Calculate the partial derivative of with y:
When , by the same induction as before, is initially decreasing, but turns to increase after. So the maximum is .
Since , the equal sign will never hold.
As for the case of , which can be classified in the discussion when H < 2R, thus we get:
When , the volume ratio is less than 1/3.
But If , is monotone decreasing, then the maximum is , which and the equal sigh holds when x = 2R.
And if , is initially decreasing, but turns to increase after with y. y1 and y2 are two roots of the equation ,
and the maximum of is .
When , ; when , ; when , , i.e. will decrease firstly, then increase and finally decrease again, and we get:
.
Since
Set , calculate its derivative and get:
Setting , then
We need a lot of complicated calculation to get the sign of N’(t) in the case when , which is very time-consuming. Here we introduce a more straight-forward method through graphing. With the help of MATLAB [2], we can draw the picture of R * N’(t).
Code is shown below:
t = 1:0.01:1.15;
y = 1/3 − 4/(27 * t2) − 2/9. * sqrt(4 − 3 * t2) + 2/27 * 1./(t2). * sqrt (4 − 3 * t2) − 16/27 * 1/(t2 * sqrt(4 − 3 * t2)) + 8/9 * 1/(sqrt(4 − 3 * t2));
plot(t, y)
Picture is shown below:
Hence holds all long, i.e. is monotone increasing.
Consequently, gets maximum at when .
The maxim us value is:
Thus, when , the volume ratio is less than 1/3.
In summary,when ,in the range of , The ratio of the inscribed elliptical cone volume to the volume of the cylinder is less than or equal to one third , and the equal sign holds when .
Case (2): when :
and last same,
When :
The variation of is exactly the same as the first situation when , that is he ratio of the inscribed elliptical cone volume to the volume of the cylinder is less than or equal to one third,
When :
The variation of is also the same as the first situation when , that is the ratio of the inscribed elliptical cone volume to the volume of the cylinder is less than or equal to one third , and the equal sign holds when .
Note: we need to point out that in case 3 and case 4, this paper gives different examples of the inscribed elliptical cone, whose bottom oval area is a possible maximum value. This means that, in some cases, the maximum area of the ellipse cannot reach the value that is given in this paper, but this won’t influences the conclusion .In addition, the maximum area of the oval can be reached when .
5. Summary
In this paper, we studied the maximum volume ratio of the inscribed elliptical cone in four different situations, 1) the most common case when the volume ration is 1/3; 2) the volume ration is strictly less than 1/3; 3) the volume ratio is less than or equal to 1/3, and the equal sign holds when , (This is a rather special case); 4) the volume ratio is less than or equal to 1/3, and the equal sigh holds when and .
6. Future Study
In this paper, we studied the maximum volume ratio of the inscribed elliptical cone to the cylinder. In the future study, we can expand the research area from cylinder to elliptical cylinders, cuboids and prisms. With the similar method, we can study the maximum volume ratio of the inscribed elliptical cone and the inscribed pyramid.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Niu, Y.S. and Li, L.Y. (2018) Study on the Maximum Volume of Inscribed Elliptical Cone inside a Cylinder. Journal of Applied Mathematics and Physics, 6, 1793-1815. https://doi.org/10.4236/jamp.2018.69154
References