Modern Economy, 2011, 2, 830-833
doi:10.4236/me.2011.25092 Published Online November 2011 (http://www.SciRP.org/journal/me)
Monopoly and Economic Efficiency: Perspective from an
Efficiency Wage Model
Bo Zhao
School of International Trade and Economics, University of International Business and Economics, Beijing, China
Received June 8, 2011; revised July 23, 2011; accepted August 19, 2011
Abstract
The objective of this paper is to analyze the efficiency consequences of monopoly from the perspective of an
efficiency-wage model based on Shapiro and Stiglitz (1984). An important innovation of our model is that a
firm can raise the probability that a shirking worker is detected by increasing its effort or investment in the
monitoring of workers. By comparing with the competitive equilibrium we find that monopoly is associated
with higher unemployment rate and less monitoring. Surprisingly, however, monopoly is not necessarily
dominated by perfect competition in terms of economic efficiency.
Keywords: Monopoly, Economic Efficiency, Unemployment, Efficiency Wage
1. Introduction
It is well-known that monopoly causes inefficient alloca-
tion of resources. Traditionally, deadweight losses, pro-
ductive inefficiencies and rent seeking activities are cited
as reasons for efficiency losses of monopoly. However,
there is one area of potential efficiency losses of monop-
oly that so far has rarely been explored in microeco-
nomic theory, that is, the effects of monopoly on unem-
ployment. Given that output is an increasing function of
labor, reduction in output by a monopoly will normally
cause a reduction in labor employed. Therefore, it seems
plausible that monopoly cause higher rate of unemploy-
ment.
On the other hand, however, the effect of monopoly on
economic efficiency, if taking unemployment into con-
sideration, is not that clear and has not been studied
deeply in microeconomic theory. Therefore, the main
objective of this paper is to analyze the efficiency con-
sequences of monopoly from the perspective of an effi-
ciency wage model of unemployment based on Shapiro
and Stiglitz [1]. In this model a monopolist has to offer a
wage high enough to induce workers to expend efforts on
the job. An important feature of our model is that a mo-
nopolist can raise the probability of shirking detection by
increasing its effort or investment in the monitoring of
workers1. Using this model we find that monopoly does
not necessarily lead to lower welfare level than perfect
competition. This result is surprising in light of the
common belief about the welfare losses of monopoly.
The rest of this paper is organized as follows. Section
2 presents the model and compares the monopoly equi-
librium with the competitive equilibrium. Section 3 ana-
lyzes the welfare consequence of monopoly and presents
the main results from simulations. And conclusions are
in section 4.
2. The Model
Consider an industry served by a monopolist2, whose
objective is to maximize profits. The demand for the
good produced by the monopolist is represented by
()pPQ


, where p is the price and Q is the output with
() 0PQ


and 2() ()0PQP Q Q



 (to ensure the
monopolist’s marginal revenue is decreasing in output),
and 0


()Ys FeL
measures the market size. The monopolist
produces the good according to the production function

with () 0F


()F and , where Y is
the output, L is the number of workers employed, e is the
effort level expended by the representative worker
(hence, eL represents the effective amount of labor em-
0
1Shapiro and Stiglitz [1] discuss informally the case of endogenous
monitoring. They indicate that in general it is impossible to ascertain
whether the competitive equilibrium entails too much or too little em-
p
loyment.
2Thus, we do not distinguish the firm’s wage and the economy-wide
wage. Alternatively, we may assume that there are many monopolized
industries in the economy and it can be shown that this assumption
does not shatter our major results in this paper.

831 B. ZHAO
ployed by the firm), and s is an exogenous technology
parameter.
To incorporate unemployment into the model, we use
the efficiency wage model of Shapiro and Stiglitz [1].
Specifically, we assume that workers may shirk (i.e. ex-
erting no effort) on the job. The firm, however, cannot
perfectly observe workers’ effort. In other words, if a
worker shirks, there is some probability, denoted by q,
that the worker will be caught and fired. In the standard
Shapiro-Stiglitz efficiency wage model, the detection
probability q is taken as exogenous. In our model, we
endogenize q by assuming that q is a function of the ef-
fort and/or investment by the firm in monitoring the
workers, with
()qqm() 0qm

 and () 0qm



,
where m denotes the monitoring level.
To discourage workers from shirking, the firm has to
pay a wage high enough (i.e. the efficiency wage or non-
shirking wage):

*
()
e
wwe abr
qm
 

(1)
where, 0w is the unemployment benefit received by
an unemployed worker; a denotes the job acquisition rate,
b is the natural separation rate and r represents the in-
tertemporal discount rate.
Taking the efficiency wage into consideration, the
monopolist’s optimization problem is written as:



,
max π() ()
()
()
mL PsFeL sFeL
e
weabrLHm
qm
 

 





(2)
where ()
H
m
0
is the cost of monitoring workers with
and 3. ()H () 0H 
Note that in the steady state of the labor market, the
flow into and the flow out of the unemployment pool per
unit time are equal. That is,

bLa NL or

abLNL (3)
Then the first order conditions for Equation (2) can be
rewritten as:

2
() () 0
()
eL qmbNrHm
NL
qm







 (4)


2() ()()
()()
s
ePsFeLFeLFeL
s
ePsFeLF eL


 


0
()
ebN
we r
qmN L


 
 



Let L = Am(m) and L = Bm(m) denote the functional re-
lationships implied by Equations (4) and (5), respectively.
Thus, graphically, the intersection of these two curves in
the (m, L) space is the monopoly equilibrium


**
,
mm
mL .
Proposition 1. Both curves, L = Am(m) and L = Bm(m),
are strictly upward sloping in the (m, L) space. Moreover,
at the equilibrium point, the slope of L = Am(m) is greater
than the slope of L = Bm(m). As a result, there is a unique
monopoly equilibrium4.
Now consider a perfectly competitive industry, where
all firms are price-takers. The representative firm’s opti-
mization problem is:


,
max()( )
()
mL
e
psFeLw ea brLHm
qm





 







(6)
Equilibriums in the product and the labor markets re-
quire that


()pPsFeL   and or

bLa NL


abLNL

. Then the first order conditions for
Equation (6) can be rewritten as:

2
() () 0
()
qm bN
eLrHm
NL
qm








 (7)


()()
0
()
sePsF eLFeL
ebN
we r
qmN L






 





(8)
Let L = Ac(m) and L = Bc(m) be the curves implied by
Equations (7) and (8), respectively. Then the intersection
of these two curves


**
,
cc
mL represents the levels of
monitoring and employment in the competitive equilib-
rium.
Proposition 2. Both curves, L = Ac(m) and L = Bc(m),
are strictly upward sloping in the (m, L) space. Moreover,
at the equilibrium point, the slope of L = Ac(m) is greater
than the slope of L = Bc(m). Therefore, there is a unique
competitive equilibrium.
Note that the comparison of Equations (4) and (7) in-
dicates that L = Am(m) and L = Ac(m) are exactly the
same curve in the (m-L) space. To determine the effi-
ciency consequences of monopoly, compare the monop-
oly equilibrium with that under perfect competition (as
shown in Figure 1) to obtain:
Proposition 3. Relative to a perfectly competitive mar-
ket, a monopolist employs fewer workers and invests less
in the monitoring of workers. That is, and
*
m
mm



(5)
*
c
**
mc
LL

.
Since the quantity produced is an increasing function
of employment, Proposition 3 in turn implies that the
3It should be noted that the monitoring cost here is assumed to be inde-
p
endent of the number of workers. Alternatively, for future research, it
may take the form of h(m)L.
4Based on the assumptions made above, it can be shown that the second
order conditions are satisfied. This ensures the existence of the equilib-
rium.

B. ZHAO
832
Figure 1. Monopoly equilibrium vs. competitive equilibrium.
monopolist produces a smaller output and accordingly
sets a higher price than a competitive firm. On the sur-
face, these effects of monopoly appear to be the same as
in the standard monopoly case. However, there are more
factors at play in this model. Intuitively, a monopolist
has a tendency to restrict output because it faces a down-
ward sloping demand curve. As a result of this tendency,
employment level falls, which tends to push down the
non-shirking wage. In our model this has an additional
effect because it induces the monopolist to reduce the
level of monitoring, causing a further fall in employ-
ment.
3. Welfare Effects of Monopoly
Given that this is a partial equilibrium model, we use the
total surplus as the measure of welfare. Note that com-
pared with the standard textbook model of monopoly, we
have an additional group of agents in our model, the
workers. In principle, the measure of total welfare should
also take into consideration the utility of workers. This
raises an additional issue of how to treat the unemploy-
ment benefits:
1) If the unemployment benefits are financed by lump
sum taxes on consumers, they are merely a wealth trans-
fer and as such should not be included in the total sur-
plus;
2) Alternatively, if there are no government transfer
payments and the unemployment benefits merely repre-
sent the value that an unemployed worker obtain from
home production, the unemployment benefits should be
included in the total surplus;
3) In addition, the conventional measure of total sur-
plus that takes into consideration the welfare of consum-
ers and the firms only (i.e. excluding the workers).
Our welfare analysis in what follows uses the first type
of total surplus5:
**
0()d()
Q
TSP QQeLHm
*
(9)
It is easy to obtain **
00
()d ()d
cm
QQ
P
QQ PQQ,
, m
*
c
eL 
*
m
eL * ()( )
c
*
H
mHm

**
cm
E
eL LH


 


 
since m and .
Thus, monopoly may lead to a higher social welfare than
perfect competition does. Specifically, if and
only if
**
c
LL
TS
*
( )Q
mQ
m


**
cm
mm
c
TS
()d
g
QQ

m

*
*
c
m
CS
P




*
()
c
H
m H





 (10)
The left hand side of Equation (10) is the sum of the
difference of worker’s efforts put into production (ΔE)
and the difference of monitoring cost (ΔH). And the right
hand side is the difference of gross consumer surplus
(ΔCSg).
In what follows we conduct numerical simulations us-
ing a version of our model with specific functional forms.
The objectives of these simulations are to provide con-
crete examples for the welfare effects of monopoly, in
comparison with the competitive benchmark.
Our simulation results, based on the specific func-
tional forms and parameter values presented in Table 1,
show that the total surplus under monopoly is not neces-
sarily lower than that under perfect competition. As we
can see from Figures 2 and 3, monopoly improves wel-
fare if, ceteris paribus, market size (α) is relatively large
or unemployment benefit (w) is relatively small6.
These numerical simulations, together with the general
analysis demonstrate that
Proposition 4. Monopoly is not always dominated by
perfect competition in terms of economic efficiency if an
efficiency wage is offered and unemployment is taken
into consideration.
4. Conclusions
In this paper, by constructing an efficiency-wage model
that takes into account the firm’s choice of monitoring,
Figure 2. Comparison of welfare: monopoly vs. competition
varying market size). (
5It can be demonstrated that the similar results will be obtained if the
6Indeed, we also find examples that when separation rate is relatively
high (say b > 0.24) or technology shock is relatively low (say
0.3
s

0.8), the total surplus under monopoly is larger than that unde
r
p
erfect competition. To avoid verbosity, we do not present them here.
other two measures are used.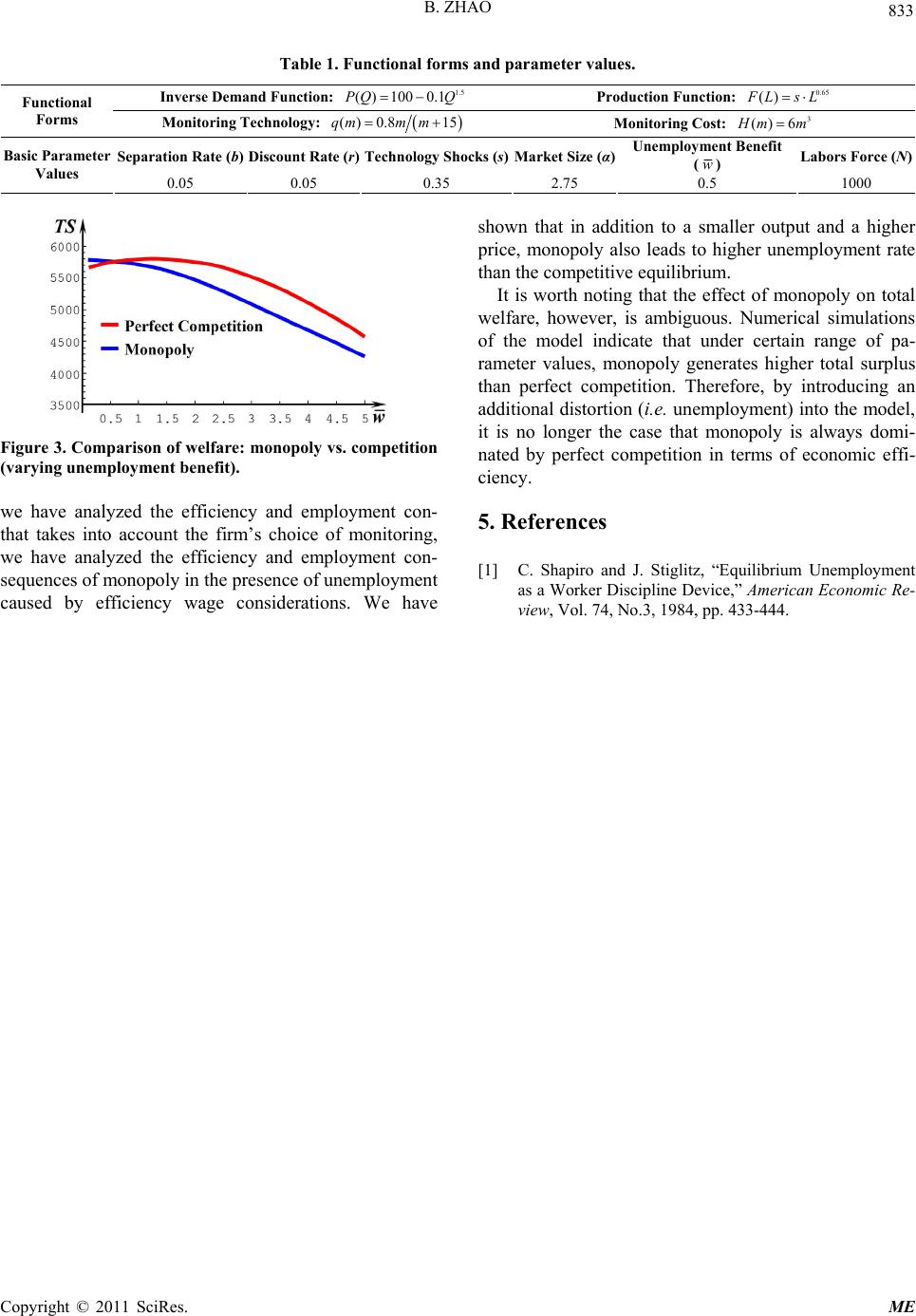

B. ZHAO
833
Table 1. Functional forms and parameter values.
Inverse Demand Function: 1.5 ( )1000.1
P
QQ Production Function:
0.65
()
F
LsL
Functional
Forms Monitoring Technology:


() 0.815qmm m Monitoring Cost: 3 ()6
H
mm
Separation Rate (b) Discount Rate (r)Technology Shocks (s)Market Size (α)Unemployment Benefit
(w) Labors Force (N)
Basic Parameter
Values 0.05 0.05 0.35 2.75 0.5 1000
Figure 3. Comparison of welfare: monopoly vs. competition
(varying unemployment benefit).
we have analyzed the efficiency and employment con-
that takes into account the firm’s choice of monitoring,
we have analyzed the efficiency and employment con-
sequences of monopoly in the presence of unemployment
caused by efficiency wage considerations. We have
shown that in addition to a smaller output and a higher
price, monopoly also leads to higher unemployment rate
than the competitive equilibrium.
It is worth noting that the effect of monopoly on total
welfare, however, is ambiguous. Numerical simulations
of the model indicate that under certain range of pa-
rameter values, monopoly generates higher total surplus
than perfect competition. Therefore, by introducing an
additional distortion (i.e. unemployment) into the model,
it is no longer the case that monopoly is always domi-
nated by perfect competition in terms of economic effi-
ciency.
5. References
[1] C. Shapiro and J. Stiglitz, “Equilibrium Unemployment
as a Worker Discipline Device,” American Economic Re-
view, Vol. 74, No.3, 1984, pp. 433-444.