Modern Economy, 2011, 2, 804-813
doi:10.4236/me.2011.25089 Published Online November 2011 (http://www.SciRP.org/journal/me)
China’s Savings and Current Account Balance: A
Demographic Tr ansition Perspective
Chao Zhu
School of Finance, Capital Un iversity of Economics and Business,
Beijing, China
Received July 7, 2011; revised August 13, 2011; accepted August 26, 2011
Abstract
In this paper, we build an overlapping generation model to analyze how China’s family planning policy af-
fects the demographic structure and the dependency ratios. We also employ the Cointegration Test and
Granger Causality Test to examine the relationship between Chinese population dependency ratios and the
national savings rate, as well as the relationship between relative productivity differences and the national
current account balance. We find that the family planning policy can be sustainable with respect to these
metrics. The current account balance reflects the transfer of savings over time and space. We posit that the
demographic structure determines the savings transfer over time, while the relative productivity difference
determines the savings transfer across the space. This transfer does not change the total welfare calculated on
a national or generational basis. Consequently, focusing on improving the consumption rate to boost the
economy without consideration of demographic structure transition warrants further serious discussion.
Similarly, too much attention to short-term current account surplus or deficit is not productive.
Keywords: Savings Rate, Current Account Balance, Demographic Structure, Family Planning Policy
1. Introduction
According to Modigliani Life Cycle Hypothesis [1],
people tend to save or dissave at different ages to smooth
consumption their entire life spans. Thus, demographic
structure should be regarded as an important variable in
determining the savings rate. Following this strategy,
scholars study the relationship between savings rates and
demographic change, analyzing whether savings rates are
a function of demographic change and then trying to es-
timate them. But the empirical finding s are no t cons istent.
For example, Modigliani and Cao [2] find an obvious
cointegration relationship between the savings rate and
the dependency ratio in China. They attribute China's
high savings rate mainly to high growth and demo-
graphic change. However, Kraay [3] uses China’s pro-
vincial panel data of household savings from 1978 to
1989 to find that the impact of the dependency ratio on
savings was not statistically significant. Horioka and
Wan [4] believe the impact of China's dependency ratio
on the savings rate is only significant in a quarter of the
sample. Zheng [5] divides the dependency ratio into
youth dependency ratio and old-age dependency ratio.
The results show that the savings rate negatively corre-
lates with the youth dependency ratio, and positively
correlates with the old-age dependency ratio. Li et al. [6]
conducts a similar analysis using China’s provincial
panel data, but the results are quite different. They find
that the youth dependen cy ratio has a very small positive
impact on savings, while the impact of old-age depend-
ency ratio on both consumption and savings is not sig-
nificant.
Actually, due to frequent population mobility and free
transfer of social security account between provinces, the
country’s overall data is far more convincing than the
provincial data in terms of the relationship between po-
pulation and economic variables. Moreover, the provin-
cial data might complicate the analysis.
Another common deficiency of the previous research
is that China’s external economic imbalance is not taken
into account. Chen and Hu [7] make efforts to incorpo-
rate China’s family planning policy into the Blanch-
ard-Fischer inter-temporal model to relax the constant
democratic structure hypothesis. They conclude that the
current account surplus is the optimal target of China’s
external balance and prepares an aging population, but

C. ZHU 805
no empirical analysis is given in the paper.
In an open economy, savings can be divided into in-
ternal savings and external savings. The former refers to
domestic savings and the latter is the current account
surplus. Thus, if demograph ic structure is correlated with
the savings rate, it might also be an important determi-
nant of external equilibrium. Coale and Hoover [8] pro-
posed the controversial hypothesis that a country’s rising
fertility rate and falling infant mortality rate will result in
heavy youth dependency burden (youth dependency) on
young families and young governments (his findings
were partly based on the data from the large number of
new governments established after World War II). Huge
consumption leads to fewer savings. Thus, in order to
finance the large-scale consumption and investment
needed to recover their economies, they have to rely on
foreign capital inflows, namely, foreign capital depend-
ency, in the form of current account deficit. Asia is a
typical example.
But results from Goldgerger [9] and Ram [10] do not
support this hypothesis. Nearly 40 years later, Higgins
and Williamson [11] test the hypothesis again with the
Asian panel data. They find that increasing savings rates
results from the falling youth dependency ratio over the
past 30 years. Thus, external capital dependence in Asia
will end and the region will beg in to export capital in the
form of current account surplus. However, the conclu-
sion differs slightly across countries. For China, the sur-
plus was completely under capital flows control in the
sample period. In this case, the conclusion is not appli-
cable.
Then, are the savings rate, investment rate and current
account surplus correlated with demographic structure?
Do current account surpluses occur in young societies
and current account deficits in aging societies? In other
words, external savings are preparing for when the future
population ages? Is it possible that the current account
surplus results from the relatively faster increase in
China’s productivity rather than demographic change?
This paper tries to answer these questions using China’s
empirical data. For simplicity, and to enhance the ex-
planatory power of our results, we focus on demographic
variables. We also decompose the total dependency ratio
into the youth dependency ratio and the old-age depend-
ency ratio to investigate whether they might have differ-
ent impacts on dependent variables. Also, based on tradi-
tional Chinese values, people tend to spend more on the
youth than on the elderly, other things being equal. Such
unique feature of Chinese consumption behavior will be
taken into consideration. This is another point on which
this paper differs from previous work.
We find that China’s family planning policy can be
sustainable. Relaxing the policy now or in the next few
years might be unable to cope with the arrival of a peak
of social maintenance. The demographic structure re-
sulting from the family planning policy determines the
savings rate, and is the price paid for China’s future
demographic structure. From an inter-temporal perspec-
tive, the current account balance is just the transfer of
savings over time and space. In this sense, China need
not be too concerned about the current short-term current
account surplus.
2. Demographic Structure Transition under
the Family Planning Policy
This paper will only consider the age structure of China’s
population. Modigliani [1] believes the savings rate
might be correlated with age structure rather than other
structures of population. Another consideration is that,
due to natural disasters, political reason and family plan-
ning policy, China has experienced dramatic changes in
age structure in recent decades.
The dependency ratios are often taken as the sub stitute
indicators of population age structure to measure the
social burden of a country. The youth dependency ratio
is the number of persons 0 to 14 years per one hundred
persons 15 to 64 years. The old-age dependency ratio is
the number of person s 65 years and over p er one hun dr ed
persons 15 to 64 years. The total dependency ratio is the
number of persons under age 15 plus persons aged 65 or
older per one hundred persons 15 to 64. It is the sum of
the youth dependency ratio and the old-age dependency
ratio1.
Now we present a multi-period overlapping generation
model to analyze the impact of China’s family planning
policy on the demographic structure and consider the
sustainability of the policy. We start with some assump-
tions. 1) We divide the life cycle into five age intervals,
respectively, 0 - 14, 15 - 30, 31 - 45, 46 - 64 and 65 years
old and over. Among them, No. 1 interval corresponds
the numerator of youth dependency ratio; No. 5 interval
corresponds the numerator of old-age dependency ratio;
whereas the middle three intervals correspond the de-
nominator of the dependency ratio (15 - 64) approxi-
mately. We treat it with five equal intervals in order to
correspond with the dependency ratio, and more impor-
1People under the age of 18 generally do not have their own income in
China. If the college students are counted, the age will be extended to
22. China’s retirement age is 60 for men and 55 for women, assuming
the same proportion of men and women, the average retirement age is
57.5 years. It is earlier than the retirement age of 65 in most developed
countries. So, if the age of 14 and 64 years are the critical points, we
are underestimating China's dependency ratio. However, when we
study the relationship between the savings (including external and
internal savings) and the population dependency ratio, as long as the
data are comparable in the sample period, this difference seems not to
change the results significantly.

C. ZHU
806
tantly, to keep consistent when every age interval grows
older to the next interval2. 2) We set 1982 as the starting
year when China began to implement strict family plan-
ning policy, assuming two persons in every interval. 3)
People tend to give birth when they are 30 years old. So
the third interval will be the next generation of the first
interval. 4) We define China’s family planning policy as:
first, one coup le may only bear one ch ild; second, if both
husband and wif e are the only child of their parents, they
can have two children. Other policy details in different
provinces and cities are ignored here. 5) The “relaxation ”
of the family planning policy means that even the parents
who are not only children themselves still can have more
than one child, and we assume they wish to have only
two children. Table 1 shows the transition of age struc-
ture under fami l y planni n g po l i cy .
Before the implementation of family planning policy
(Period 0), the demograph ic structure is in stable equilib-
rium, when the total dependency ratio is 67.
In period 1, the family planning policy becomes effec-
tive. Youth population declines, the total dependency
ratio drops to 50 from 67 with the denominator being
constant. The popu lation burden begins to relax.
In period 2, the young and old populations do not
change. But the youth population decreased in period 1
will reduce the labor force in period 2 correspondingly.
Youth dependency ratio, old-age dependency ratio and
total dependency ratio (60) were improved, but still
lower than the original value 67. Both period 1 and 2 can
be seen as demographic dividend periods resulting from
the family planning policy.
At the beginning of period 3 (corresponding to 2013
approximately), China will face three options: 1) Keep
family planning policy forever; 2) Relax the family-
planning policy from period 3; 3) Keep family planning
policy till period 5, and then relax.
In the first case, the couples who are both only chil-
dren born in periods 1 and 2 can have two children in
periods 3 and 4. Both young people and old people will
keep constant, but the labor force continues to fall. The
total dependency ratio will reach a peak value of 100.
The country will suffer significant increasing of the
population bu rden. After entering period 5, child ren who
are born in period 3 and are not only children, so they
can have only one child again. Thus, the dependency
ratio will repeat the cycle beginning from 1982. The
population will decline dramatically and enjoy demo-
graphic dividends again.
In the second case, we suppose China begins to relax
family-planning policy from period 3 or period 4. All
couples can have two children, regardless of whether
they themselves are only children or not. We have as-
sumed that a couple wishes to have only two children.
Actually, the couples who are born in period 1 are all
only children. They already have the right to have two
children, even if the policy is not relaxed. In other words,
relaxing the family planning policy now would not help
to avoid the coming peak. The demographic structure
would be similar to that of the first case; the peak of de-
pendency ratio will arrive in the 2040s in either case.
From period 5, the demographic structure will be re-
balanced, the total dependency ratio will return to the
initial value of 67.
In the third case, the family planning will be kept in
period 3 and period 4, and r elaxed in period 5. This case
is not different from the second case, except that the total
dependency ratio will return to the initial value of 67 in
period 7, rather than in period 5 as in the third case.
Now we look at China’s population data to test
whether it fits the above analysis. Figure 1 shows 100
years of China’s dependency ratio data (1950-2050). The
data before 1978 are from the World Bank and United
Nations Population Division database. Data from 1978 to
2007 are from the “China Statistical Yearbook” and
“China Population Statistics Yearbook”. For some miss-
ing data, we use the fertility rate and mortality rate data
to estimate the arithmetic mean value. The data after
2007 are from the forecast of Zhou [13], under the as-
sumption that China’s family planning policy remains
unchanged.
China began to implement its strict family planning
policy in 1982. As a result, the youth dependency ratio
began to decrease, the old-age dependency ratio in-
creased slowly, and the total dependency ratio declined
to the bottom in the early 20th century. This period of
time (from 1982 to the early 20th century) can be com-
pared to periods 1 and 2, when the total dependency ratio
declined from 67 to 50 as Table 1 shows and the demo-
graphic dividend occurred. In period 3 (approximately
throughout the 2020s), the elderly population will grow
and the total dependen cy ratio will increase to its peak in
2To be sure, it is still not accurate. The former three intervals are 15
years long, whereas, the fourth one is 18 years long. We have to ignore
the slight inaccuracy to correspond the fifth intervals to the old-age
dependency ratio by doing so. Figure 1. China’s dependency ratio (1950-2050). (Sources:
BSC [12] and Zhou [13]). N

C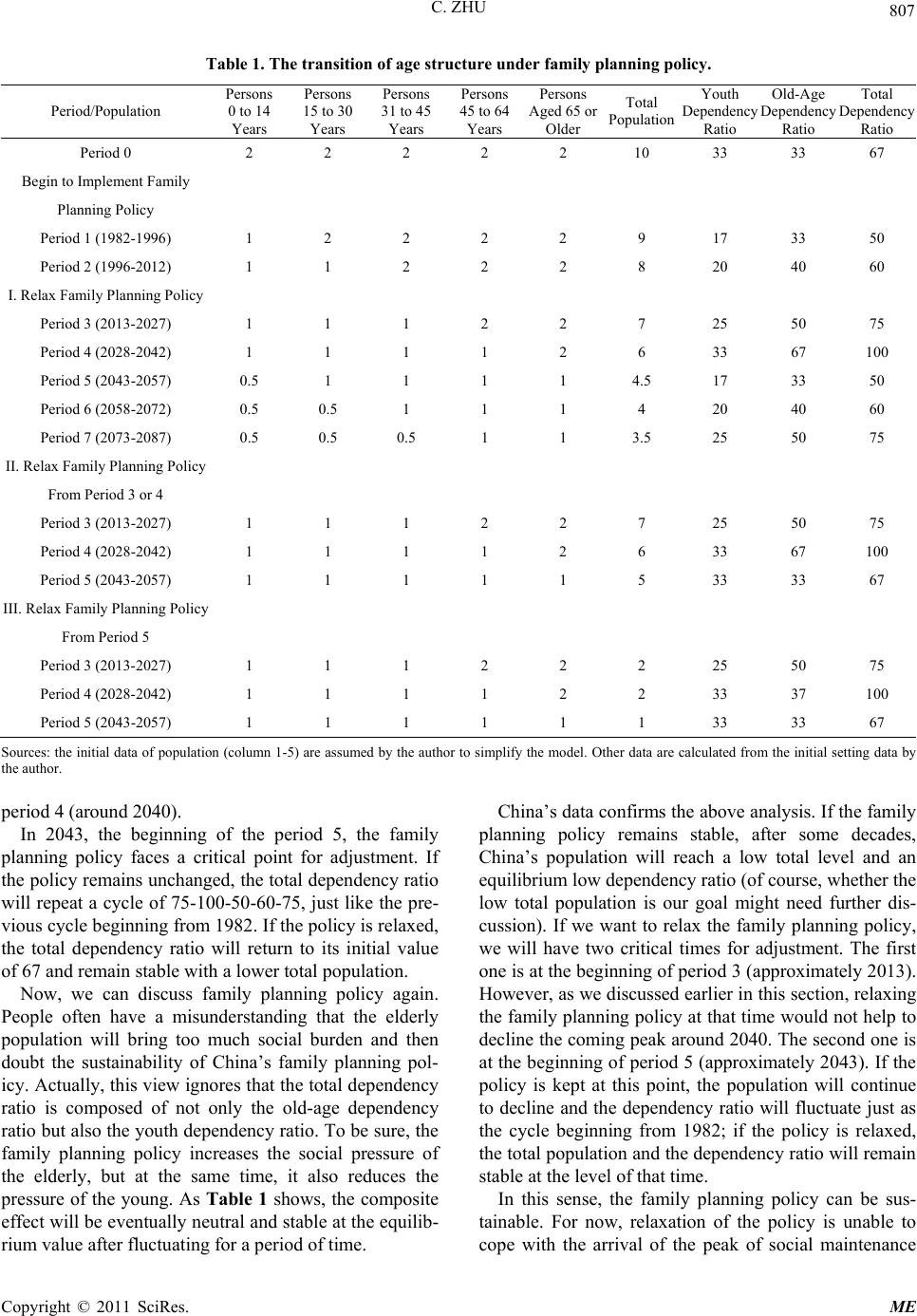. ZHU
807
Table 1. The transition of age structure under family planning policy.
Period/Population Persons 0 to 14
Years
Persons
15 to 30
Years
Persons
31 to 45
Years
Persons
45 to 64
Years
Persons
Aged 65 or
Older
Total
Population
Youth
Dependency
Ratio Old-Age
Dependency
Ratio
Total
Dependency
Ratio
Period 0 2 2 2 2 2 10 33 33 67
Begin to Implement Family
Planning Policy
Period 1 (1982-1996) 1 2 2 2 2 9 17 33 50
Period 2 (1996-2012) 1 1 2 2 2 8 20 40 60
I. Relax Family Planning Policy
Period 3 (2013-2027) 1 1 1 2 2 7 25 50 75
Period 4 (2028-2042) 1 1 1 1 2 6 33 67 100
Period 5 (2043-2057) 0.5 1 1 1 1 4.5 17 33 50
Period 6 (2058-2072) 0.5 0.5 1 1 1 4 20 40 60
Period 7 (2073-2087) 0.5 0.5 0.5 1 1 3.5 25 50 75
II. Relax Family Planning Policy
From Period 3 or 4
Period 3 (2013-2027) 1 1 1 2 2 7 25 50 75
Period 4 (2028-2042) 1 1 1 1 2 6 33 67 100
Period 5 (2043-2057) 1 1 1 1 1 5 33 33 67
III. Relax Family Planning Policy
From Period 5
Period 3 (2013-2027) 1 1 1 2 2 2 25 50 75
Period 4 (2028-2042) 1 1 1 1 2 2 33 37 100
Period 5 (2043-2057) 1 1 1 1 1 1 33 33 67
Sources: the initial data of population (column 1-5) are assumed by the author to simplify the model. Other data are calculated from the initial setting data by
the author.
period 4 (around 2040) .
In 2043, the beginning of the period 5, the family
planning policy faces a critical point for adjustment. If
the policy remains unchanged, the total dependency ratio
will repeat a cycle of 75-100-50-60-75, just like the pre-
vious cycle beginning from 1982. If the policy is relaxed,
the total dependency ratio will return to its initial value
of 67 and remain stable with a lower total popu lation.
Now, we can discuss family planning policy again.
People often have a misunderstanding that the elderly
population will bring too much social burden and then
doubt the sustainability of China’s family planning pol-
icy. Actually, this view ignores that the total d ependency
ratio is composed of not only the old-age dependency
ratio but also the youth dep endency ratio. To be sure, the
family planning policy increases the social pressure of
the elderly, but at the same time, it also reduces the
pressure of the young. As Table 1 shows, the composite
effect will be eventually neu tral and stable at the equilib-
rium value after fluctuating for a period of time.
China’s data confirms the above analysis. If the family
planning policy remains stable, after some decades,
China’s population will reach a low total level and an
equilibrium low dependency ratio (of course, whether the
low total population is our goal might need further dis-
cussion). If we want to relax the family planning policy,
we will have two critical times for adjustment. The first
one is at the beginning of period 3 (approximately 2013).
However, as we discussed earlier in this section, relaxing
the family planning policy at that time would not help to
decline the coming peak around 2040. The second one is
at the beginning of period 5 (approximately 2043). If the
policy is kept at this point, the population will continue
to decline and the dependency ratio will fluctuate just as
the cycle beginning from 1982; if the policy is relaxed,
the total population and the dependency ratio will remain
stable at the level of that time.
In this sense, the family planning policy can be sus-
tainable. For now, relaxation of the policy is unable to
cope with the arrival of the peak of social maintenance

C. ZHU
808
pressure. However, if the policy is kept unchanged,
China may enjoy a desirable total population with the
same dependency ratio. Thirty years from now (around
2040), what should we do: relax the policy or keep it? It
depends on how much population is desirable at that
time.
A question may be whether the total population will
decrease by 50% just as estimated in Table 1. This re-
searcher believes it depends on the actual effect of the
policy. Theoretically, if the policy is carried out as
strictly as officially stated, women’s total fertility rate
would be one. But in fact, China had never reached this
level. Total fertility remained at 2 or more during the
first 10 years and dropped to 1.34, where it remained
even in 2005. This also explain s why the current popula-
tion did not decrease at the scale estimated in Table 1.
Because of these similar reasons, the actual dependency
ratios differ slightly from those in the model, though they
share a common rule. The model can provide some ideas
for policy, but specific policy decisions should be based
on more accurate actual data.
3. Empirical Results
3.1. Variables and Data
To illustrate the impact of demographic structure on in-
ternal and external savings, we take the savings rate (SR),
the investment rate (IR), the current account balance
(NER) as the dependent variables, assuming all the cur-
rent account balance are net exports of goods and ser-
vices. They are all expressed by the percentage of GDP
of the same year. We take the total dependency ratio
(TDR), youth dependency ratio (YDR) and old-age de-
pendency ratio (ODR) to denote the population structure
variables. GDP per capita growth rate represents produc-
tivity movement; the relative productivity increase (RPI)
represents productivity growth differences between
China and the world, denoted by per capita GDP growth
rate; CRPI represents the relative productivity increase.
We set 1978 as the starting year and assume that the
starting value is zero. Data are from ERS. International
Macroeconomic Data Set. Figure 2 shows the movement
of China’s GDP calculated by expenditure approach for
several deca des.
The investment rate rose dramatically due to the
“Great Leap Forward” began in 1958, and then decline
sharply to the bottom because of “Three Years of Natural
Disasters” (1959-1962). Another bottom during 1967,
1968, and 1969 is attributed to the beginning of the Cul-
tural Revolution. In 1978, th e Chinese economy beg an to
take off. The current account surplus also accelerated.
The data interval is from 1978 to 2007. We give up a
Figure 2. China’s GDP and its components (1952-2007).
(Sources: NBSC [12]. Notes: Because savings are the sum of
investment and net exports, the total area represents the
savings rate).
longer data interval mainly because of the following
considerations. First, the data before the reform and
opening up policy cannot be obtained. Second, some
parts of the data—like net exports—are almost zero,
which cannot satisfy the data variability. Third, if the
data intervals are too long, it might be difficult to reflect
the huge institutional changes such as economic policy
and family planning policy in the transitional economies.
3.2. Unit Roots Test
In this paper, we take ADF to test for stationary of vari-
ables to avoid “spurious regression”. Table 2 shows the
results.
3.3. Cointegration and Granger Causality Test
In this paper, we focus on the relationship between two
variables. Intuitively, the demographic structure might
affect the economic variables like savings rate but the
economic variables might have a very weak or even no
effect on population. Thus, we prefer the Engle-Granger
(EG) two-step cointegration test rather than VAR model.
The relative productivity increase (RPI) is a stationary
time series and can not participate in a cointegration test
here, but the cumulative relative productivity increase
(CRPI) is integrated of order one and can be cointegrated.
The results are shown in Table 3.
3.3.1. Savings Rate and Dependency Rati o s
According to the life cycle theory, in the absence of
economic growth and new wealth, young people will
save for future consumption and dissave as they age.
Thus, a young population will be accompanied with high
savings rate, while an aging population should be ac-
companied with a low savings rate. If the dependency
ratios are used as a proxy for demographic structure, then,
theoretically, the higher total dependency ratio needs
ore immediate consumption. In other words, the total m

C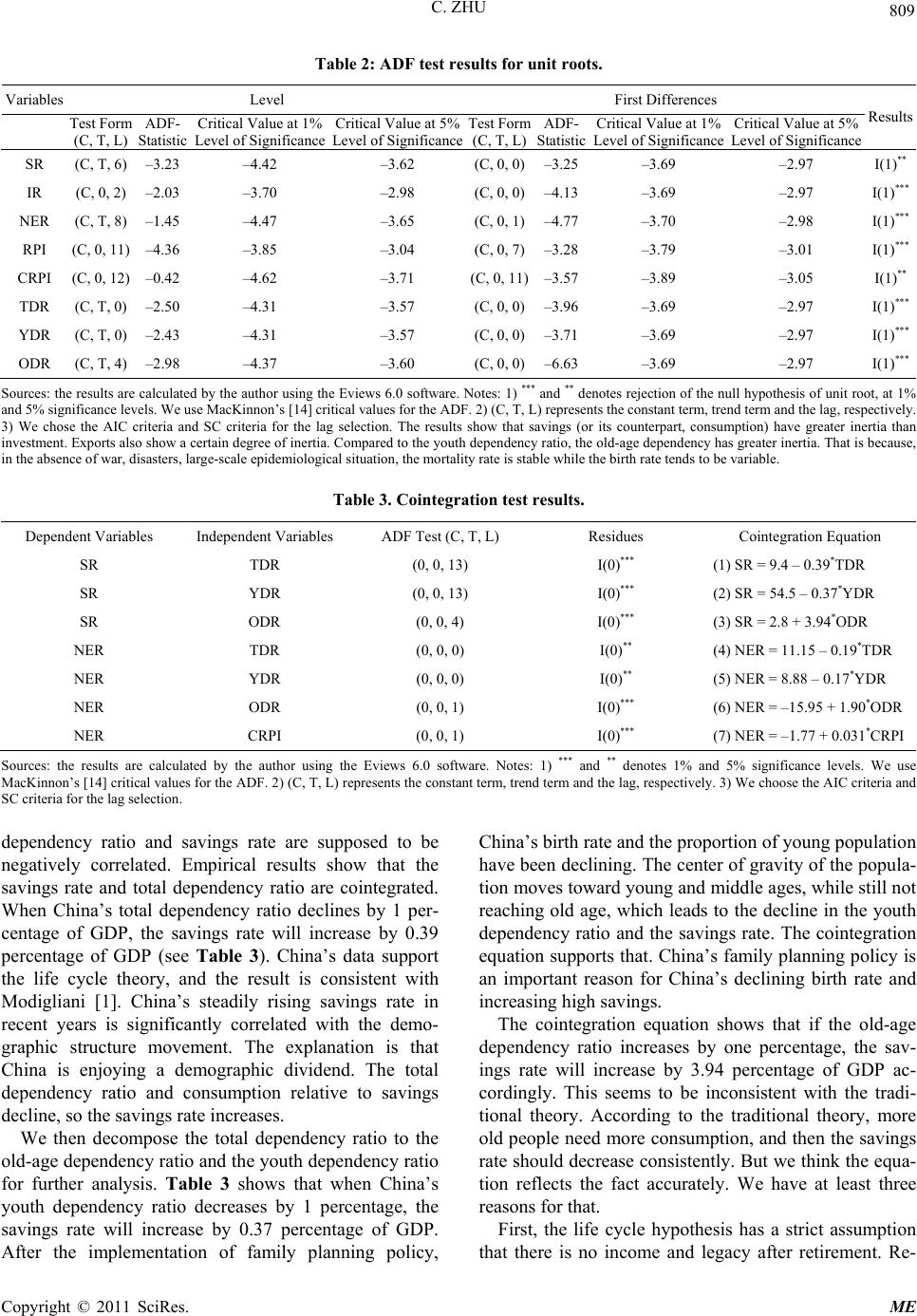. ZHU
809
Table 2: ADF test results for unit roots.
Variables Level First Differences
Test Form
(C, T, L) ADF- Statistic Critical Value at 1% Level of Significance Critical Value at 5% Level of SignificanceTest Form (C, T, L)ADF- Statistic Critical Value at 1% Level of Significance Critical Value at 5% Level of Significance
Results
SR (C, T, 6) –3.23 –4.42 –3.62 (C, 0, 0)–3.25–3.69 –2.97 I(1)**
IR (C, 0, 2) –2.03 –3.70 –2.98 (C, 0, 0)–4.13–3.69 –2.97 I(1)***
NER (C, T, 8) –1.45 –4.47 –3.65 (C, 0, 1)–4.77–3.70 –2.98 I(1)***
RPI (C, 0, 11) –4.36 –3.85 –3.04 (C, 0, 7)–3.28–3.79 –3.01 I(1)***
CRPI (C, 0, 12) –0.42 –4.62 –3.71 (C, 0, 11)–3.57–3.89 –3.05 I(1)**
TDR (C, T, 0) –2.50 –4.31 –3.57 (C, 0, 0)–3.96–3.69 –2.97 I(1)***
YDR ( C, T, 0) –2.43 –4.31 –3.57 (C, 0, 0)–3.71–3.69 –2.97 I(1)***
ODR ( C, T, 4) –2.98 –4.37 –3.60 (C, 0, 0)–6.63–3.69 –2.97 I(1)***
Sources: the results are calculated b y the autho r using the Ev iews 6.0 so ftware. Notes: 1 ) *** and ** denotes rejection of the null hypothesis of unit root, at 1%
and 5% significance levels. We use MacKinnon’s [14] critical values for the ADF. 2) (C, T, L) represents the constant ter m, trend term and the lag, respectively.
3) We chose the AIC criteria and SC criteria for the lag selection. The results show that savings (or its counterpart, consumption) have greater inertia than
investment. Exports also show a certain degree of inertia. Compared to the youth dependency ratio, the old-age dependency has greater inertia. Th at is b ecau se,
in the absence of war, disaste rs , l arge-scale epidemiological situation, the mortality r ate is stable wh il e the birth rate tends to be variable.
Table 3. Cointegration test results.
Dependent Variables Independent Variables ADF Test (C, T, L) Residues Cointegration Equation
SR TDR (0, 0, 13) I(0)*** (1) SR = 9.4 – 0.39*TDR
SR YDR (0, 0, 13) I(0)*** (2) SR = 54.5 – 0.37*YDR
SR ODR (0, 0, 4) I(0)*** (3) SR = 2.8 + 3.94*ODR
NER TDR (0, 0, 0) I(0)** (4) NER = 11.15 – 0. 19*TDR
NER YDR (0, 0, 0) I(0)** (5) NER = 8.88 – 0.17*YDR
NER ODR (0, 0, 1) I(0)** * (6) NER = –15.95 + 1.90*ODR
NER CRPI (0, 0, 1) I(0)*** (7) NER = –1.77 + 0.031*CRPI
Sources: the results are calculated by the author using the Eviews 6.0 software. Notes: 1) *** and ** denotes 1% and 5% significance levels. We use
MacKinnon’s [14] critical values for the ADF. 2) (C, T, L) represents the constant term, trend term and the lag, respectively. 3) We choose the AIC criteria and
SC criteria for the lag selection.
dependency ratio and savings rate are supposed to be
negatively correlated. Empirical results show that the
savings rate and total dependency ratio are cointegrated.
When China’s total dependency ratio declines by 1 per-
centage of GDP, the savings rate will increase by 0.39
percentage of GDP (see Table 3). China’s data support
the life cycle theory, and the result is consistent with
Modigliani [1]. China’s steadily rising savings rate in
recent years is significantly correlated with the demo-
graphic structure movement. The explanation is that
China is enjoying a demographic dividend. The total
dependency ratio and consumption relative to savings
decline, so the savings rate increases.
We then decompose the total dependency ratio to the
old-age dependency ratio and the youth dependency ratio
for further analysis. Table 3 shows that when China’s
youth dependency ratio decreases by 1 percentage, the
savings rate will increase by 0.37 percentage of GDP.
After the implementation of family planning policy,
China’s birth rate and the propor tion of youn g populatio n
have been declining. The center of gravity of the popu la-
tion moves toward young and middle ages, while still not
reaching old age, which leads to the decline in the youth
dependency ratio and the savings rate. The cointegration
equation supports that. Chin a’s family planning policy is
an important reason for China’s declining birth rate and
increasing hi gh savi ng s .
The cointegration equation shows that if the old-age
dependency ratio increases by one percentage, the sav-
ings rate will increase by 3.94 percentage of GDP ac-
cordingly. This seems to be inconsistent with the tradi-
tional theory. According to the traditional theory, more
old people need more consumption, and then the savings
rate should decrease consistently. Bu t we think the equa-
tion reflects the fact accurately. We have at least three
reasons for that.
First, the life cycle hypothesis has a strict assumption
that there is no income and legacy after retirement. Re-

C. ZHU
810
tired people can only spend their previous savings for
consumption. But this assumption is not satisfactory. In
China, the elderly in rural areas rarely rely on previous
savings. On the contrary, their new revenue can often
cover the current consumption. Sometimes, they even
have new savings. In urban areas, the elderly may even
leave some legacy to the next generation, rather than
zero, assumed by life cycle hypothesis. So, at least for
now, the elderly w ho are counted in the total d ependen cy
ratio in China are not generating complete dependency
needs.
Second, due to China’s family planning policy, China’s
current family structure is transforming from a pyramid
shape to that of an inverted pyramid. The elderly can no
longer rely on their descendants due to the “4-2-1” fam-
ily structure3. They have to prepare excess savings for
themselves rather than “bringing up sons to support par-
ents in their old age”, as the ancient Chinese idiom goes.
Thus, in the short run (such as the transition period last-
ing for 1 - 2 generations), the increase in the elderly
population will make the savings rate increase, not de-
crease. But in the long run, if the family planning policy
continues, the elderly will gradually decrease to the nor-
mal and stable level. The excess savings will diminish
slowly. If the family planning policy is relaxed, then
young population will grow. The excessive savings ef-
fect will soon disappear, b ecause the old people can rely
on “bringing up sons to support parents in their old age”
again.
Third, the values contained in another Chinese idiom,
“long to see one’s child become a dragon when he/she
grows up”4 have a unique impact. Under the influence of
this traditional culture, children often spend more than
the elderly. Therefore, although the old-age dependency
ratio increases, the increase of consumption due to the
positive impact of th e old-age dependency ratio might be
less than the decrease of consumption due to the falling
the youth dependency ratio. The savings rate is more
sensitive to the youth dependency ratio than to the
old-age dependency ratio.
Therefore, an important explanation for the increase of
China’s savings rate in recent years is the decline in the
total dependency ratio. Among them, the decreased
youth dependency ratio dramatically increases the sav-
ings rate. The impact of the old-age dependency ratio on
the savings rate is opposite to that of the youth depend-
ency ratio. However, the impact of the latter is larger
than the former. So taking them both into consideration,
the decrease in the total dependency ratio can explain the
increase in the savings rate.
3.3.2. Domestic Savings vs. External S a vi n gs
Savings means future consumption and can be divided
into investment and net exports. Investment (labeled as
internal savings) can be regarded as the purchase of
goods to produce more future products. The current ac-
count surplus (labeled as external savings) can be inter-
preted as expor ting savings to foreign countries and then
obtaining the claim for future capital and/or goods of
them in the form of foreign exchange or other securities.
Demographic dividend can explain why China has a
high savings rate, but cannot explain why the savings
rate is greater (or less) than investment rate, and subse-
quently, the current account balance. We initially thought
that demographic structure could explain the current ac-
count surplus just as Chen and Hu [7] concluded. Unfor-
tunately, we fail to find empirical evidence in this paper
to support that conclusion. Considering that the Granger
causality test is sensitive to the lag order, we exhaust all
the lag orders of 1 - 9 to do the test. The result is com-
pletely consistent. For all the lag orders, the demographic
structure does not Granger cause current account surplus,
and similarly, current account surplus does not Granger
cause the demographic structure, although the latter is
obvious.
It should be noted that the excessive savings flowing
out to other countries in the form of current account sur-
plus will return to China together with its earnings from
abroad even tually in the fo rm of a current accoun t deficit.
Later generations will still benefit from the previous ex-
cess savings. On the contrary, if a country’s domestic
savings are insufficient to support high investment, for-
eign capital will flow in to fill the gap in the form of the
country’s current account deficit. But the foreign capital
(or future product) will flow from the host country back
to the investors in the form of the country’s future cur-
rent account surplus. In this sense, the United States is
just the temporary place for excess savings of creditor
countries. U.S. residents can only enjoy the goods pro-
duced by their own savings shares. Therefore, from the
perspective of transfers across generations, the current
excessive consumption the U.S enjoys now must be at
the cost of insufficient consumption of the next genera-
tion. The current account balance is just the transfer of
excess savings over time and space. A country’s savings
will transfer between different generations and different
countries. In terms of space, this kind of transfer does not
change the total welfare of a country; in terms of time, it
does not change the total welfare of d ifferent generations
either.
3“4” refers to two sets of grandparents, “2” refers to two parents, “1”
refers to one child.
4“Wang Zi Cheng Long”. “Dragon” in Chinese often implies a very
successful person.
3.3.3. The Relative Productivity Difference and the
Current Account Balance
Then, what can explain China’s current account surplus?

C. ZHU 811
Let us look at the problem from a different perspective.
Is it possible that the current account surplus is only a
passive outcome rather than a provocative choice under
the competitive market? High savings rate makes current
account surplus possible. Intuitively, given high savings
rate, the current account surplus may be interpreted by
three reasons. First, savings cannot be transformed into
investment, due to depressed domestic financial system.
We set aside this complicated issue in this paper. The
second is the exchange rate regime and level. Wang [15]
has shown that the RMB exchange rate and trade balance
are not significantly correlated. This paper will not focus
on this view either. The third is that China’s higher pro-
ductivity increase relative to the world results in savings
spillover (exports). This paper will test the explanatory
power of the third reason.
Cumulative productivity increases over years, rather
than differences of productivity in a certain year, deter-
mines market competitiveness. Therefore, we use the
cumulative stock of RPI (CRPI) as the independent vari-
able of the current account balance. Two variables are
first-order stationary sequences and can be tested using
E-G cointegration. Results show they are cointegrated.
The cointegration Equation (7) (see Table 3) shows that
when CRPI increases by one percentage point, the cur-
rent account surplus increases by 0.03 percentage of
GDP.
The Granger causality test shows the cumulative dif-
ference of relative productivity Granger causes the cur-
rent account surplus for the lag orders of 1, 2, 3, 4, 5, 6,
and 7 at 5% or 10% significance. But for the lag orders
of 8 and 9, it is not statistically significant. Overall, it can
be said that relative productivity statistically Granger
causes the current account surplus. However, the current
account surplus does not cause the relative productivity.
Intuitively, the former might not be the determinant of
the latter. Our Granger test confirms this.
Let us now summarize the determination of the curren t
account balance. In period 1, savings are dependent on
the current and future demographic structure as discussed
above. Among the savings, how much of savings is allo-
cated to external savings (current account surplus) is
dependent on the relative productivity in period 1. Rela-
tively higher productivity yields stronger market com-
petitiveness, which then allows for more savings spill-
over (exports). In period 2, the savings in period 1 are
consumed. The curr ent account surplu s should flow back
to meet the need of expected consumption. At the same
time, among the savings in period 2, how much savings
is allocated to external savings (current account surplus)
is again dependent on the relative productivity in period
2. We may conclude that the relative productivity deter-
mines the “spillover” of current account surplus, while
the demographic structure determines the “return” of the
current account deficit.
4. Forecast
In this section, we try to forecast the future demographic
structure, savings rate and current account balance.
However, two points need to be emphasized. First, all
forecasts are model-based. We assume the above cointe-
gration relationship does ex ist and reflects the underlying
rule. If the current equation itself is false, the result
might be misleading. Second, all forecasts rely on the
principle of Ceteris Paribus, that is, we do not take other
factors outsid e of cointegr ation equation into account.
We still use the total depend ency ratio data from 2008
to 2050 in Zhou [13] to forecast the savings rate using
cointegration Equation (1) and the current account sur-
plus using cointegration Equation (7). To reduce the er-
rors, we use the arithmetic average value of every 10
years rather than every single year.
According to the forecast, the total dependency ratio
will steadily increase for the next 40 years. As mentioned
earlier in Section 3, this would reduce the savings. The
savings rate will decrease slowly to 38%, returning to th e
level of the late 1980s. If the long -run rule exists, we are
currently saving for the future consumption. Higher
consumption in young populations implies less con-
sumption in older populations. Consequently, we should
review the policy of raising the consumption rate to
boost economy. Perhaps it may not have the desired ef-
fect, and might be at the cost of future social mainte-
nance insolvency.
The current account surplus will be smaller, decreas-
ing from the current 9% to 1%. There is a discernible
trend that the savings are returning to China. Three ex-
planations may help to explain that. First, China has be-
gun to use current savings for the arrival of the peak de-
pendency ratio. Second, the savings rate will decline du e
Table 4. Forecast results.
Year/Item Average in
2011-2020 Average in 2021-2030 Average in 2031-2040 Average in 2041-2050
Total
Dependency 42.5 45.8 51.3 53.6
Ratio
Savings Rate 42.8 41.5 39.4 38.5
Current
Account 3.1 2.4 1.4 0.96
Balance (% of GDP)
Sources: NBSC [12], Zhou [13] and the author’s calculation using the
cointegration equations in Table 3.

C. ZHU
812
to the higher dependency ratios, which also leads to less
capital outflow. Third, China’s productivity increase
relative to the rest of the world will become smaller. We
think the above trends ar e fairly certain. In th is sense, we
need not be too concerned about the current short-term
current account surplus. In the long run, we can still ob-
tain external balance.
5. Conclusions and Policy Implications
In this paper, we build an overlapping generation model
to analyze how the family planning policy af fects demo-
graphic structure and the dependency ratios. We also
employ the Cointegration and Granger Causality Tests to
explore the relation between population dependency ra-
tios and the savings rate as well as the relationship be-
tween relative productivity differences and the current
account balance. The main findings are summarized as
follows.
First, the existing family planning policy can be sus-
tainable. Under the family planning policy, the depend-
ency ratios will decline to the bottom line in parallel with
the demographic dividend, and then increase to a peak.
After a period of difficulty, the dependency ratio will
rebalance to a low level together with a low total popu la-
tion. From the perspective of dependency ratios, relaxing
the policy now or in the next few years may be unable to
cope with the arrival of the peak of social maintenance.
Meanwhile, an unchanged policy would be helpful to
obtain a desired total population. Whether China should
relax the policy in the 2040s depends on the level of
population desired at that time.
Second, the demographic structure represented by the
dependency ratios determines the savings rate. An im-
portant explanation for China’s high savings rate in re-
cent years is the decline of the total dependen cy ratio and
subsequent demographic dividend resulting from the
family planning policy. The impact of the old-age de-
pendency ratio on the savings rate is opposite to that of
the youth dependency ratio. However, the impact of the
latter is larger than the former. From a policy perspective,
if current savings are needed for future consumption,
raising consumption to boost China’s economy is ques-
tionable. The high savings rate now is the price paid for
China’s future demographic structure.
Third, from an inter-temporal perspective, the current
account balance is just the transfer of savings over time
and space. Demographic structure determines savings
transfers over time, while the relative productivity dif-
ference determines savings transfers across space. Both
kinds of transfer do not change the total welfare calcu-
lated on a national or generational basis. Specifically
speaking, the relative productivity determines the “spill-
over” of current account surplus, while the demographic
structure determines the “return” of the current account
deficit. In the long run, China will use current saving s fo r
the arrival of the peak dependency ratio. Also, China’s
productivity increases relative to the rest of the world
will become smaller. In this sense, we need not be too
concerned about the current short-term current account
surplus.
6. References
[1] F. Modigliani, “The Life Cycle Hypothesis of Saving and
Intercountry Differences in the Saving Ratio,” In: W. A.
Elits, M. F. Scott and J. N. Wolfe, Eds., Induction, Growth
and Trade, Essays in Honor of Sir Roy Harrod, Oxford,
1970.
[2] F. Modigliani and S. L. Cao, “The Chinese Saving Puzzle
and the Life-Cycle Hypothesis,” Journal of Economic
Literature, Vol. 42, No. 1, 2004, pp. 145-170.
doi:10.1257/002205104773558074
[3] A. Kraay, “Household Saving in China,” World Bank
Economic Review, Vol. 14, No. 3, 2000, pp. 545-570.
[4] C. Y. Horioka and J. Wan, “The Determinants of House-
hold Saving in China: A Dynamic Panel Analysis of Pro-
vincial Data,” NBER Working Papers No. 12723, 2006.
[5] C. D. Zheng, “An Empirical Study of the Relationship
between Population Structure and Savings Ratio in Dif-
ferent Regions,” Population & Economy, Vol. 14, No. 6,
2007, pp. 1-5.
[6] W. X. Li, C. S. Xu and C. R. Ai, “The Impacts of Popula-
tion Age Structure on Household Consumption in China:
1989-2004,” Economic Research Journal, Vol. 54, No. 4,
2008, pp. 118-129.
[7] Z. J. Chen and C. T. Hu, “How Large Should China’s
Current Account Target Be? A Demographic Structure
Perspective,” Modern Economic Science, Vol. 31, No. 4,
2009, pp. 1-11.
[8] A. Coale and E. Hoover, “Population Growth and Eco-
nomic Development in Low-Income Countries,” Prince-
ton University Press, Princeton, 1958.
[9] A. Goldberger, “Dependency Rates and Savings Rates:
Further Comment,” American Economic Review, Vol. 63,
No. 1, 1973, pp. 232-33.
[10] R. Ram, “Dependency Rates and Aggregate Savings: A
New International Cross-Section Study,” American Eco-
nomic Review, Vol. 72, No. 3, 1982, pp. 537-544.
[11] M. Higgins and G. W. Jeffrey, “Asian Demography and
Foreign Capital Dependence,” NBER Working Papers No.
5560, 1996.
[12] NBSC (National Bureau of Statistics of China), “China
Statistical Yearbook,” China Statistics Press, Beijing,
1980-2008,.
[13] W. B. Zhou, “The Forecast and Reasearch on the De-
pendent Ratio For the Next Five Decades,” Statistical
Research, Vol. 21, No. 11, 2004, pp. 35-38.

C. ZHU
813
[14] J. G. MacKinnon, “Numerical Distribution Functions for
Unit Root and Cointegration Tests,” Journal of Applied
Econometrics, Vol. 11, No. 6, 1996, pp. 601-618.
doi:10.1002/(SICI)1099-1255(199611)11:6<601::AID-JA
E417>3.0.CO;2-T
[15] R. Y. Wang, “The Demographic, Trade Balance, and
Exchange Rate Policy Adjustment in China,” The Journal
of World Economy, Vol. 26, No. 9, 2003, pp. 3-9.