Algorithms for Integer Factorization Based on Counting Solutions of Various Modular Equations

doi:10.4236/ijcns.2011.411083

Int. J. Communications, Network and System Sciences, 2011, 4, 675-682

doi:10.4236/ijcns.2011.411083 Published Online November 2011 (http://www.SciRP.org/journal/ijcns)

Algorithms for Integer Factorization Based on Counting

Solutions of Various Modular Equations

Boris S. Verkhovsky

Computer Science Department, New Jersey Institute of Technology, Newark, USA

E-mail: verb73@gmail.com

Received September 20, 2011; revised October 27, 2011; accepted November 6, 2011

Abstract

This paper is a logical continuation of my recently-published paper. Security of modern communication

based on RSA cryptographic protocols and their analogues is as crypto-immune as integer factorization (iFac)

is difficult. In this paper are considered enhanced algorithms for the iFac that are faster than the algorithm

proposed in the previous paper. Among these enhanced algorithms is the one that is based on the ability to

count the number of integer solutions on quadratic and bi-quadratic modular equations. Therefore, the iFac

complexity is at most as difficult as the problem of counting. Properties of various modular equations are

provided and confirmed in numerous computer experiments. These properties are instrumental in the pro-

posed factorization algorithms, which are numerically illustrated in several examples.

Keywords: RSA Cryptography, Integer Factorization, Modular Quadratic Equations, Modular Bi-Quadratic

Equation, Equivalent Problems, Rabin Protocol

1. Introduction and Problem Statement

Security of modern communication based on RSA or

Rabin cryptographic protocols and their analogues is as

crypto-immune as difficult is the integer factorization

(iFac) [1-3]. This paper is a continuation of the paper [4].

In that paper is considered a factorization algorithm of

semi-prime n=pq for two cases: where either both factors

p and q are non-Blum primes i.e.,

p=q=1(mod4), (1.1)

or at least one factor is a non-Blum prime. In this paper

an iFac algorithm is provided, which also works if both

factors p and q are Blum primes, i.e.,

p=q=3(mod4). (1.2)

The SQUAR-algorithm discussed in [4] is based on

several properties (formulated as propositions and con-

jectures) of dual modular elliptic curves, where b is a

positive integer:





222

modyxxbn



; (1.3)

and . (1.4)





222

modyxxbn

Let us reiterate some of these properties and then con-

sider their generalizations.

Let p=q=1(mod4); n=pq; let P(n,b) and M(n,b) denote

the number of points on elliptic curves (EC) (1.3) and

(1.4) respectively.

For the sake of brevity, we call P(n,b) and M(n,b) the

counts.

Conjecture 1.1: Consider n=pq, and let primes p and

q satisfy (1.1);

if





,1 ,1Pn Mn



; (1.5)

then for every integer b





,Pnb Mnb



,; (1.6)

otherwise, for every integer b





,Pnb Mnb



,

. (1.7)

If n is a prime and (1.5) holds, then for every b also

holds





,,2Pnb Mnbn











. (1.8)

Remark 1.1: Conjecture1.1 plays an important role in

the design of the iFac described in [4]; further details are

provided in the Appendix.

Proposition 1.2: If the factors p and q are congruent

to 1 modulo n=pq, then the following identities hold for

non-negative integers m and s:

B. VERKHOVSKY

676

if

mod 42ms 



s

2



; (1.9)

then



,2 ,2

m

Pn Mn. (1.10)

Proposition 1.3: If the factors p and q are congruent

to 1 modulo n=pq, , and

1

bb

 

12

,,Pnb Mnb,

then







1

,,

2

M

nbP nb. (1.11)

The proposed iFac2 algorithm described below is less

restrictive than the integer factorization SQUAR-algo-

rithm described and analyzed in [4], because it is also

applicable if both p and q satisfy (1.1).

Proposition 1.4: {modular reduction-in-exponent}:

Consider elliptic curves





22 mod

e

yxxb n



; (1.12)

and





22 mod

e

yxxb n ; (1.13)

where ; then for every integer b>0 and e>0 the

following identities hold:

4e







mod 4

,,

ee

Pnb Pnb; (1.14)







mod 4

,,

ee

MnbMnb. (1.15)

Proof {by mathematical induction}: Consider substitu-

tions

3

:mod and :mod

2

y

Ybnx Xbn; (1.16)

into (1.12). Then after cancellation of the same term

in both parts of (1.12) we derive the EC

6

b





224

mod

e

YXXb n







. (1.17)

Repeating the substitutions (1.16) and cancellations of

term , we derive the proof of (1.14). Analogously we

proceed with the proof of (1.15).

6

b

A generalized reduction-in-exponent can be formulated

for a hyperelliptic curve {HEC}.

Proposition 1. 5: Consider HECs





mod

trd e

yxxb n ; (1.18)

and . (1.19)





mod/ mod

edtrm

trd

YXXb n







If t<d and gcd(d, r)=m, then for every integer b>0 both

HECs have equal number of points.

Proof: after appropriate substitutions, the proof is analo-

gous to the proof of Proposition 1.4 (details of the proof

and an example are provided in the Appendix}.

Special case: if m=1 and t=0, then







mod mod

rdedr

YXb n



. (1.20)

2. iFac1 Algorithm Based on EC

SQUAR-algorithm described in paper [4] requires con-

sideration of a sequence of elliptic curves with control

parameter b. Namely, for every b=1,2,3,5,··· to count the

number of points on each EC until four distinct counts

are found; {see Example 2.1 below}.

In the following algorithm we need at most three distinct

counts. Let





:,

ii

PPnb

.

The iFac1 algorithm:

1) Compute 12 1

,,,



i

PPP P until two distinct integers

are found;

2) if







1i



s

ign Pnsign Pn





(2.1)

then





1

:gcd, ;

i

pPPn



 q=n/p; (2.2)

else compute





1

:gcd ,

i

wPPn

; (2.3)

3) if w>1, then p:=w; (2.4)

else find a 3rd distinct count ;

k

P

4

)





1

:gcd, ;

k

pPPn q=n/p. (2.5)

Example 2.1: For semi-prime n=6525401, the sets

are as follows:

123 4

, , and SSS S







1

2

3

1, 7,11,17, 29,31, 41,;7012681;

2,5,13, 23,37,;6055665;

3,19,;6514053 ;

Sb L

Sb S

Sb A

 



(2.6)

S4={b=43,53,···; B=6519205}.

Therefore, the SQUAR-algorithm provided in [4] re-

quires at least fifteen basic steps, because 43 is the four-

teenth prime (2.5). Yet, since

1

PP

2



; and; (2.7)

13

PPP

2

then the 1st





13

:gcd ,

f

actorPP n

.

Hence, instead of counting points

12357 43

,,,,,,PPPPP P [4],

in fifteen elliptic curves, we determine both factors of n

after three distinct counts.

3. iFac1 Validation

Definition 3.1: A pair of counts is called a

resolventa if



,

ij

PP







gcd, 1

ij

PPn



.

If w=1 (2.1), then we need to compute the 3rd distinct

value {see Example 2.1}. However, if w>1, then we

compute the 1st factor, say, p, and then q:=n/p. The fol-

lowing proposition and examples provide explanations.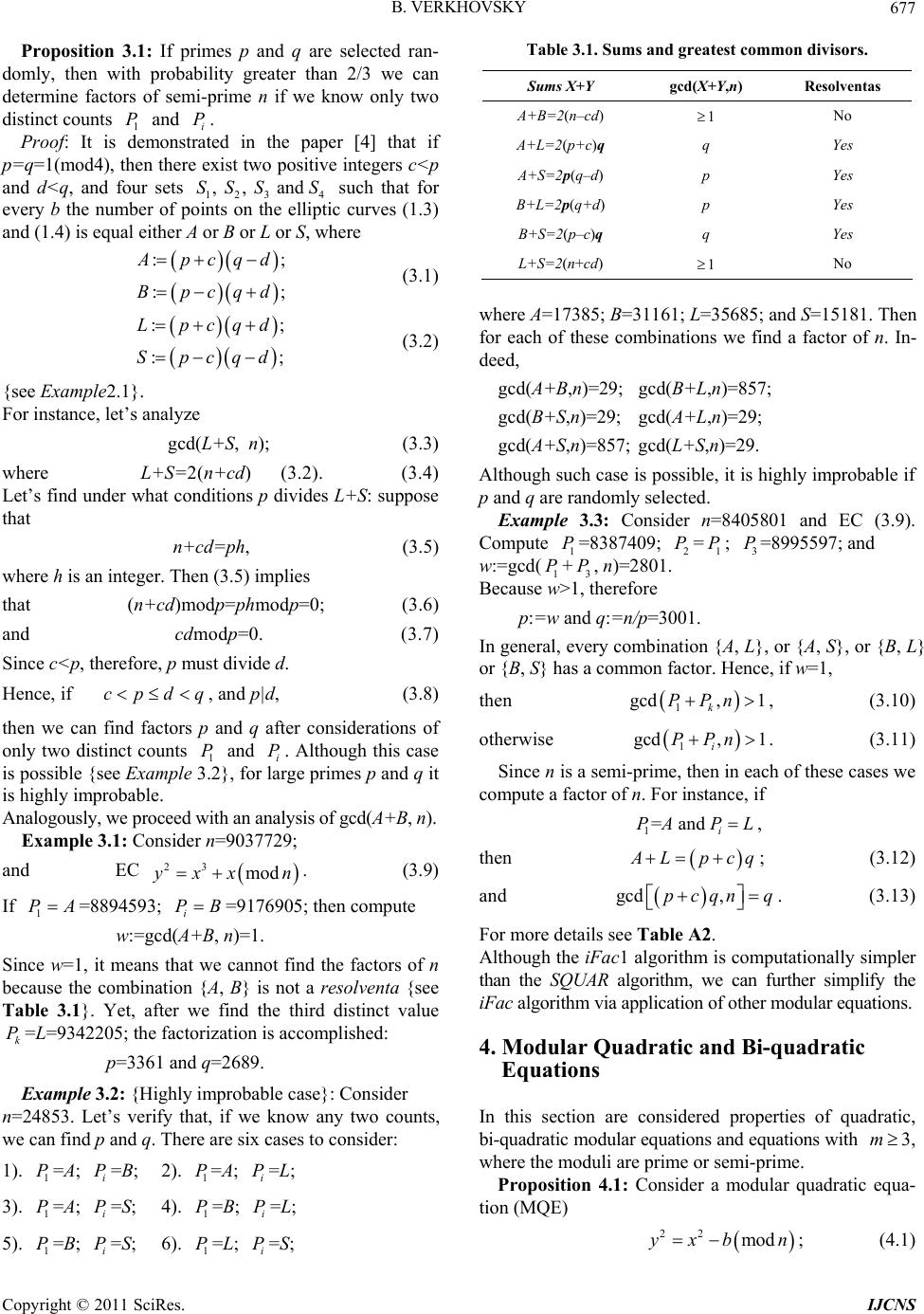

B. VERKHOVSKY677



Proposition 3.1: If primes p and q are selected ran-

domly, then with probability greater than 2/3 we can

determine factors of semi-prime n if we know only two

distinct counts and .

1i

Proof: It is demonstrated in the paper [4] that if

p=q=1(mod4), then there exist two positive integers c<p

and d<q, and four sets 123 4

such that for

every b the number of points on the elliptic curves (1.3)

and (1.4) is equal either A or B or L or S, where

P P

, , and SSS S



:;

A

pcqd

Bpcqd

 

 (3.1)





:;

Lpcqd

Spcqd

 

 



(3.2)

{see Example2.1}.

For instance, let’s analyze

gcd(L+S, n); (3.3)

where L+S=2(n+cd) (3.2). (3.4)

Let’s find under what conditions p divides L+S: suppose

that

n+cd=ph, (3.5)

where h is an integer. Then (3.5) implies

that (n+cd)modp=phmodp=0; (3.6)

and cdmodp=0. (3.7)

Since c<p, therefore, p must divide d.

Hence, if , and p|d,

(3.8) cpdq

then we can find factors p an d q after considerations of

only two distinct counts 1 and i. Although this case

is possible {see Example 3.2}, for large primes p and q it

is highly improbable.

P P

Analogously, we proceed with an analysis of gcd(A+B, n).

Example 3.1: Consider n=9037729;

and EC





23 mod

y

xx n . (3.9)

If =8894593; =9176905; then compute

1

PAi

PB

w:=gcd(A+B, n)=1.

Since w=1, it means that we cannot find the factors of n

because the combination {A, B} is not a resolventa {see

Table 3.1}. Yet, after we find the third distinct value

=L=9342205; the factorization is accomplished:

k

P

p=3361 and q=2689.

Example 3.2: {Highly improbable case}: Consider

n=24853. Let’s verify that, if we know any two counts,

we can find p and q. There are six cases to consider:

1). =A; =B; 2). =A; =L;

1

Pi

P1

Pi

P

3). =A; =S; 4). =B; =L;

1

Pi

P1

Pi

P

5). =B; =S; 6). =L; =S;

1

Pi

P1

Pi

P

Table 3.1. Sums and grea test common divisors.

Sums X+Y gcd(X+Y,n) Resolventas

A+B=2(n–cd) 1 No

A+L=2(p+c)q q Yes

A+S=2p(q–d) p Yes

B+L=2p(q+d) p Yes

B+S=2(p–c)q q Yes

L+S=2(n+cd) 1 No

where A=17385; B=31161; L=35685; and S=15181. Then

for each of these combinations we find a factor of n. In-

deed,

gcd(A+B,n)=29; gcd(B+L,n)=857;

gcd(B+S,n)=29; gcd(A+L,n)=29;

gcd(A+S,n)=857; gcd(L+S,n)=29.

Although such case is possible, it is highly improbable if

p and q are randomly selected.

Example 3.3: Consider n=8405801 and EC (3.9).

Compute 1=8387409; =; =8995597; and

w:=gcd( +, n)=2801.

PP2

P1

P3

P

1 3

Because w>1, therefore

P

p:=w and q:=n/p=3001.

In general, every combination {A, L}, or {A, S}, or {B, L}

or {B, S} has a common factor. Hence, if w=1,

then





1

gcd,1

k

PPn



, (3.10)

otherwise





1

gcd, 1

i

PPn



. (3.11)

Since n is a semi-prime, then in each of these cases we

compute a factor of n. For instance, if

1= and i

PAP L,

then





A

Lpcq



 ; (3.12)

and





gcd ,pcqnq







. (3.13)

For more details see Table A2.

Although the iFac1 algorithm is computationally simpler

than the SQUAR algorithm, we can further simplify the

iFac algorithm via application of other modular equations.

4. Modular Quadratic and Bi-quadratic

Equations

In this section are considered properties of quadratic,

bi-quadratic modular equations and equations with ,

where the moduli are prime or semi-prime.

3m

Proposition 4.1: Consider a modular quadratic equa-

tion (MQE)



22 modyxb n



; (4.1)

B. VERKHOVSKY

678

let G(n, b) denote the number of integer pairs (x, y)

{called points on quadratic curve (4.1)} that satisfy (4.1);

if n is a prime, then for every non-zero b co-prime with n



,1Gnbn;

if n is a semi-prime and n=pq, then for every non-zero b

co-prime with n





 

,1Gpqb pq 1. (4.2)

Proof is provided in the Appendix.

Conjecture 4.2: Consider a modular equation

V(p, m, b):





22 mod

m

yx bp ; (4.3)

where p is a prime; let G(p, m, b) denote the number of

points on (4.3);

if (4.3) is either a quadratic or bi-quadratic equation (i.e.,

if m=1 or m=2), and pmod4=3, then





,, 1.



Gpmbp (4.4)

if m=1 and pmod4=1, then (4.4) holds.

Table 4.1. Values of G(p, m, b).

pmod4 m=1 m=2 m ≥ 3: if gcd(m,p–1)=1

pmod4=1 1p 1

p

 1p

pmod4=3 1p 11p p

Conjecture 4 .3 : Consider a modular equation

V(n, m, b): let b>0;



22 mod

m

yx bn



1

; (4.5)

and let G(n, m, b) denote the number of points on (4.5);

if both factors p and q are primes, and if (4.5) is either a

quadratic or bi-quadratic equation (i.e., if m=1 or m=2),

then for every b>0



,,1 1Gpqmb pq ; (4.6)

if an odd prime m is co-prime with , then

for every b and m each co-prime with



1pq



n









,,1 1Gnmb pqn



 



. (4.7)

Here is called the Euler totient function.



n



Table 4.2. Values of G(pq, m, b).

m=1 m=2 m>3; if =1



gcd ,mn







p=q(mod4)=1



n







n





n



p=q(mod4)=3



n





n







n



pqmod4=3



n







n





n



Numerous computer experiments for m=2, 3, 5, 7 con-

firmed Conjecture 4.3 Thirty six examples in Table 4.3

demonstrate the correctness of the Conjecture 4.3 for

m=1, 2, 3, and 5. In italics are shown the cases, where





gcd ,











mn

>1, i.e., where (4.7) does not hold.

Table 4.3. Values of G(pq, m, b); m=1,2,3,5.

m=1 m=2 3m; if =1



gcd ,mn







65,85,

377

48,64,

336 ok 36,28

324

m=3:32,64, 224

m=5: 48,64, 336

77,161

209

60,132

180 ok 60,132

180 ok m=3: 140,308,20

m=5: 12,132, 36

55,95

187

40,72

160 ok 20,36,

140 m=3: 40, 8, 160

m=5: 8, 72, 32

{see also Table 6.1 and 6.2 below}.

The iFac algorithm described below is based on Pro-

position 4.1. This algorithm is computationally efficient

if there exists an efficient procedure (an oracle) that counts

the points on either the MQE (m=1) or bi-quadratic

equation (m=2) (4.5).

Definition 4.1: {equivalence}: Problem 1

A

is equi-

valent to problem 2

A

if their time complexities satisfy

the inequality









12

TA TA.

Definition 4.2: {strong equivalence}: Problems 1

A

and 2

A

are strongly equivalent if their time complexi-

ties and T satisfy

1 2

T





12

TT



1

.

Tables 6.1 and 6.2 illustrate Conjecture 4.2 and Conjec-

ture 4.3.

5. iFac2 Algorithm

Conjecture 4.3 can be applied to design an iFac2 algo-

rithm. As it implied from the following discussion, this

algorithm is more efficient than the SQUAR-algorithm

proposed in [4]. Yet, for the seemingly simple iFac2

algorithm we need to know how to efficiently count the

number of points G(n, m, b) on modular Equation (4.5)

for m=1 or m=2.

The algorithm

1) Select b=m=1; compute G(n) for V(n,1,1) (4.5) and

(4.6);

2) Compute



:RnGn





; (5.1)

3) Solve quadratic equation

20zRzn



; (5.2)

suppose are its roots;

12

4) {Integer factors p and q}:

and zz

21

: and :pzqz



. (5.3)

Therefore, the iFac2 problem is equivalent to the prob-

lem of counting points on the MQE (4.1).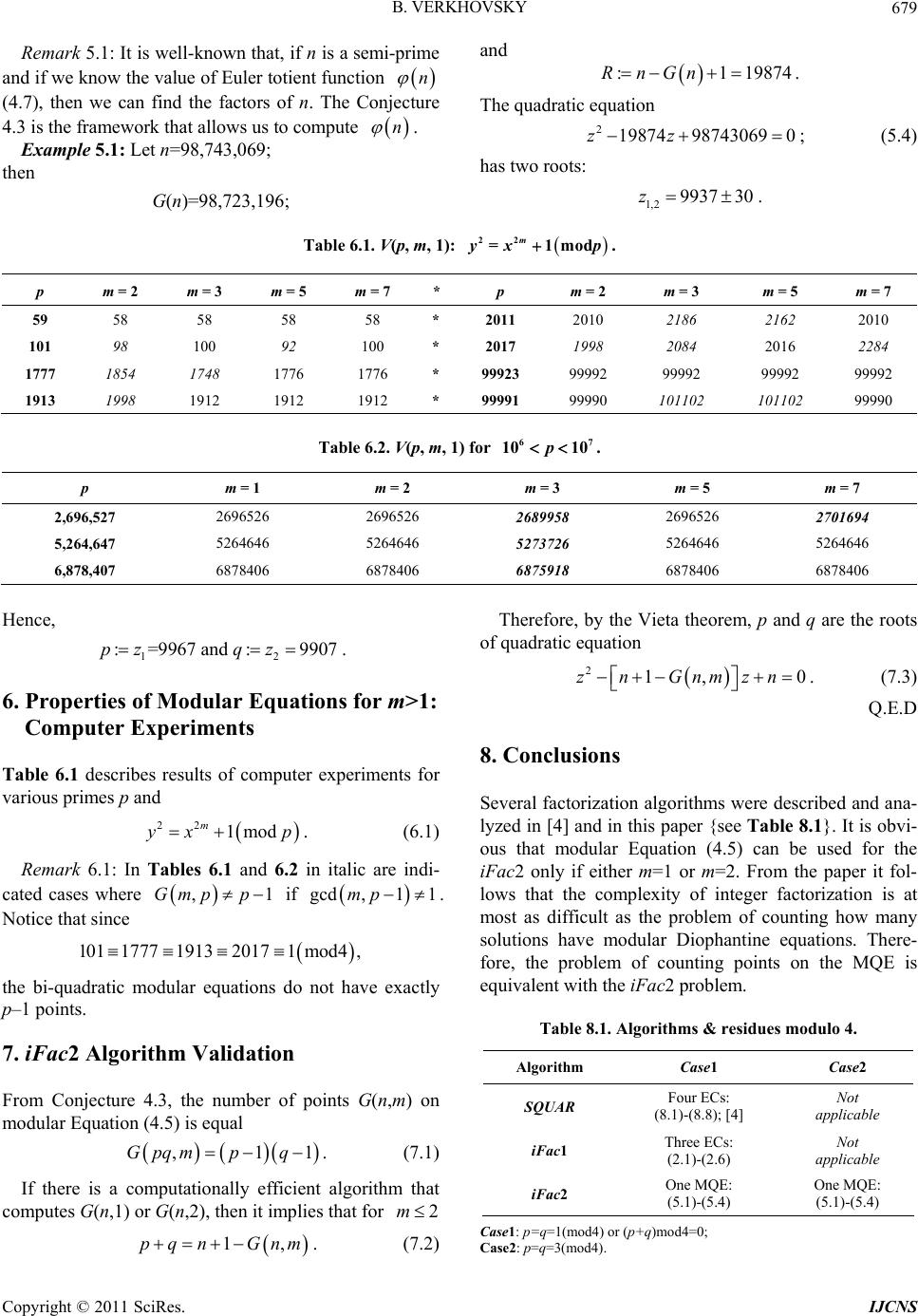

B. VERKHOVSKY

679

and

Remark 5.1: It is well-known that, if n is a semi-prime

and if we know the value of Euler totient function





n



(4.7), then we can find the factors of n. The Conjecture

4.3 is the framework that allows us to compute





n



.





:1 19874RnGn



.

The quadratic equation

21987498743069 0zz



; (5.4)

Example 5.1: Let n=98,743,069; has two roots:

then

1,2 9937 30z



.

G(n)=98,723,196;

Table 6.1. V(p, m, 1):





22

=1mod

m

yx p.

p m = 2 m = 3 m = 5 m = 7 * p m = 2 m = 3 m = 5 m = 7

59 58 58 58 58 * 2011 2010 2186 2162 2010

101 98 100 92 100 * 2017 1998 2084 2016 2284

1777 1854 1748 1776 1776 * 99923 99992 99992 99992 99992

1913 1998 1912 1912 1912 * 99991 99990 101102 101102 99990

Table 6.2. V(p, m, 1) for 67

10 10p



.

p m = 1 m = 2 m = 3 m = 5 m = 7

2,696,527 2696526 2696526 2689958 2696526 2701694

5,264,647 5264646 5264646 5273726 5264646 5264646

6,878,407 6878406 6878406 6875918 6878406 6878406

Therefore, by the Vieta theorem, p and q are the roots

of quadratic equation

Hence,

12

:=9967 and :9907pzqz.





21,zn Gnmzn0



 





. (7.3)

6. Properties of Modular Equations for m>1:

Computer Experiments Q.E.D

8. Conclusions

Table 6.1 describes results of computer experiments for

various primes p and Several factorization algorithms were described and ana-

lyzed in [4] and in this paper {see Table 8.1}. It is obvi-

ous that modular Equation (4.5) can be used for the

iFac2 only if either m=1 or m=2. From the paper it fol-

lows that the complexity of integer factorization is at

most as difficult as the problem of counting how many

solutions have modular Diophantine equations. There-

fore, the problem of counting points on the MQE is

equivalent with the iFac2 problem.





22

1mod

m

y

xp

. (6.1)

Remark 6.1: In Tables 6.1 and 6.2 in italic are indi-

cated cases where if



,1Gmp p



gcd ,1 1mp



.

Notice that since



101177719132017 1mod4,

the bi-quadratic modular equations do not have exactly

p–1 points. Table 8.1. Algorithms & residues modulo 4.

7. iFac2 Algorithm Validation Algorithm Case1 Case2

SQUAR Four ECs:

(8.1)-(8.8); [4]

Not

applicable

iFac1 Three ECs:

(2.1)-(2.6)

Not

applicable

iFac2 One MQE:

(5.1)-(5.4)

One MQE:

(5.1)-(5.4)

From Conjecture 4.3, the number of points G(n,m) on

modular Equation (4.5) is equal



,1Gpqmpq 



1. (7.1)

If there is a computationally efficient algorithm that

computes G(n,1) or G(n,2), then it implies that for 2m



Case1: p=q=1(mod4) or (p+q)mod4=0;



1,pqn Gnm



. (7.2) Case2: p=q=3(mod4).

B. VERKHOVSKY

680

9. Acknowledgements

I express my appreciation to A. Joux, D. Kanevsky, A.

Koval, R. Rubino and to reviewers for suggestions that

improved this paper.

10. References

[1] R. L. Rivest, A. Shamir and L. M. Adleman, “A Method

for Obtaining Digital Signature and Public-Key Crypto-

systems,” Communications of ACM, Vol. 21, No. 2, 1978,

pp. 120-126. doi:10.1145/359340.359342

[2] H. Elkamchouchi, K. Elshenawy and H. Shaban, “Ex-

tended RSA Cryptosystem and Digital Signature Schemes

in the Domain of Gaussian Integers,” Proceedings of the

8th International Conference on Communication Systems,

Singapore City, Vol. 1, 25-28 November 2002, pp. 91-95.

[3] M. O. Rabin, “Digitalized Signatures and Public Key Func-

tions as Intractable as Factorization,” Technical Report

MIT/LCS/TR-212, MIT Laboratory for Computer Science,

Cambridge, January 1979.

[4] Boris S. Verkhovsky, “Integer Factorization of Semi-

primes Based on Analysis of a Sequence of Modular El-

liptic Equations,” International Journal of Communica-

tions, Network and System Sciences, Vol. 4, No. 10, 2011,

pp. 609-615. doi:10.4236/ijcns.2011.410073

[5] C. Pomerance, “The Quadratic Sieve Factoring Algorithm,”

Advances in Cryptology, Proceedings of Eurocrypt’84,

LNCS, Vol. 209, Springer-Verlag, Berlin, 1985, pp. 169-

182.

[6] R. Schoof, “Counting Points on Elliptic Curves over Fi-

nite Fields,” Journal de Theorie des Nombres de Bor-

deaux, Vol. 7, No. 1, 1995, pp. 219-254.

doi:10.5802/jtnb.142

[7] K. Rubin and A. Silverberg, “Ranks of Elliptic Curves,”

Bulletin (New Series) of the American Mathematical So-

ciety, Vol. 39, No. 4, 2002, pp. 455-474.

[8] L. Dewaghe, “Remarks on the Schoof-Elkies-Atkin Al-

gorithm,” Mathematics of Computation, Vol. 67, No. 223,

1998, pp. 1247-1252.

doi:10.1090/S0025-5718-98-00962-4

[9] C. F. Gauss, “Theoria Residuorum Biquadraticorum,”

2nd Edition, Chelsea Publishing Company, New York,

1965, pp. 534-586.

B. VERKHOVSKY

681

Appendix

A1. Proof of Proposition 4.1

Consider MQE:





22 modyxb n . (A.1)

Proposition 4.1: If n is a prime, then the number of

points with non-negative x and y on quadratic curve Q(n)

is equal n–1; if n=pq, then Q(pq)=(p–1)(q–1).

Proof: Consider an integer parameter t on interval

[1, n–1]. The modular multiplicative inverse of t exists if

and only if gcd (t, n)=1.

Consider



 

112modvttbn n



 ;

and



 

112modwtbtn n



 . (A.2)

If n is a prime, then there are n–1 integers that are

co-prime with n; if n is a semi-prime and n=pq, then

there are (p–1)(q–1) integers that are co-prime with n. If

n is odd, then (1)2n is an integer; therefore both v

and w are integers.

It is easy to verify that for every t there is a unique pair

{v, w} that satisfies (A.1). Therefore, we proved that

(A.1) has at least n–1 solutions for n prime and has at

least (p–1)(q–1) if n=pq. Let us show that there are no

Paper Menu >>

Journal Menu >>