ABSTRACT

In this work, we recall definition of functions called as C-class and use the concepts of dislocated metric, b-dislocated metric, altering distance function. We prove some coincidence, fixed and common fixed point results for two pairs of weakly compatible mappings under $f-\left(\psi ,\varphi ,s\right)$ -contractive conditions and contractive conditions depended on another function T. Our theorems extend and generalize related results in the literature.

Subject Areas:

Functional Analysis, Mathematical Analysis

Keywords:

$f-\left(\psi ,\varphi ,s\right)$ Contraction, C-Class Functions, $b_d$ -Dislocated Metric Space, Coincidence Point, Common Fixed, Altering Distance Functions, Weakly Compatible Maps

1. Introduction

The study of metric fixed point theory in dislocated metric spaces was considered by P. Hitzler and A. K. Seda in [1] who introduced this metric as a generalization of usual metric, and generalized the Banach contraction principle on this space. Since then a lot of papers have been written on this topic treating the problem of existence and uniqueness of fixed points for mappings satisfying different contractive conditions, see [2] - [14] . N. Hussain et al. in [15] introduced the b-dislocated metric spaces associated with some topological aspects and properties. These spaces can be seen as generalizations of dislocated metric spaces and also as generalization of b-metric space introduced by Bakhtin in [16] and extensively used by Czerwik in [8] . Recently, there are many papers on existence and uniqueness of fixed point and common fixed point for one, two or more mappings under different types of contractive conditions in the setting of dislocated spaces and b-dislocated metric spaces.

Since altering distance functions were introduced by Khan et al. in [17] , the study of the existence of fixed points of contractive maps in metric spaces and generalized metric spaces has a lot of interest for many authors which are based on this category of functions (see [17] - [23] ). In September 2014, a class of functions called as C-class is presented by A. H. Ansari, see in [24] [25] and is important, see example 2.15.

The present paper is organized in two sections. Using concepts mentioned above, in the first section, we develop some coincidence and common fixed point theorems (existence and uniqueness) for two pairs of weakly compatible mappings in the framework of $b_d$ -dislocated metric space, using weak generalized $f-\left(\psi ,\varphi ,s\right)$ contractive conditions. In the second section, we prove common fixed point theorems for a pair of mappings using generalized $f-\left(\psi ,\varphi ,s\right)$ contractive condition and the concept of T-contractions. The related results generalize and improve various theorems in recent literature.

2. Preliminaries

Consistent with [1] and [15] , the following definitions, notations, basic lemma and remarks will be needed in the sequel.

Definition 2.1 [1] Let X be a nonempty set and a mapping $d_l:X\times X\to \left[0,\infty \right)$ is called a dislocated metric (or simply $d_l$ -metric) if the following conditions hold for any $x,y,z\in X$ :

1) If $d_l\left(x,y\right)=0$ , then $x=y$

2) $d_l\left(x,y\right)=d_l\left(y,x\right)$

3) $d_l\left(x,y\right)\le d_l\left(x,z\right)+d_l\left(z,y\right)$

The pair $\left(X,d_l\right)$ is called a dislocated metric space (or d-metric space for short). Note that for $x=y$ , $d_l\left(x,y\right)$ may not be 0.

Definition 2.2 [15] Let X be a nonempty set and a mapping $b_d:X\times X\to \left[0,\infty \right)$ is called a b-dislocated metric (or simply $b_d$ -dislocated metric) if the following conditions hold for any $x,y,z\in X$ and $s\ge 1$ :

1) If $b_d\left(x,y\right)=0$ , then $x=y$

2) $b_d\left(x,y\right)=b_d\left(y,x\right)$

3) $b_d\left(x,y\right)\le s\left[b_d\left(x,z\right)+b_d\left(z,y\right)\right]$

The pair $\left(X,b_d\right)$ is called a b-dislocated metric space. And the class of b-dislocated metric space is larger than that of dislocated metric spaces, since a b-dislocated metric is a dislocated metric when $s=1$ .

Example 2.3 If $X=R$ , then $d_l\left(x,y\right)=\left|x\right|+\left|y\right|$ defines a dislocated metric on X.

Definition 2.4 [1] A sequence $\left(x_n\right)$ in $d_l$ -metric space $\left(X,d_l\right)$ is called:

1) a Cauchy sequence if, for given $\epsilon >0$ , there exists $n_0\in N$ such that for all $m,n\ge n_0$ , we have or $\underset{n,m\to \infty }{\lim }{d}_l\left(x_n,x_m\right)=0$ ;

2) convergent with respect to $d_l$ if there exists $x\in X$ such that $d_l\left(x_n,x\right)\to 0$ as $n\to \infty$ . In this case, x is called the limit of $\left(x_n\right)$ and we write $x_n\to x$ .

A $d_l$ -metric space X is called complete if every Cauchy sequence in X converges to a point in X.

In [15] , it was shown that each $b_d$ -metric on X generates a topology ${\tau }_{b_d}$ whose base is the family of open $b_d$ -balls $B_{b_d}\left(x,\epsilon \right)=\left\{y\in X:b_d\left(x,y\right)<\epsilon \right\}$ .

Also in [15] , there are presented some topological properties of $b_d$ -metric spaces.

Definition 2.5 [15] Let $\left(X,b_d\right)$ be a $b_d$ -metric space, and $\left\{x_n\right\}$ be a sequence of points in X. A point $x\in X$ is said to be the limit of the sequence $\left\{x_n\right\}$ if $\underset{n\to \infty }{\lim }{b}_d\left(x_n,x\right)=0$ and we say that the sequence $\left\{x_n\right\}$ is $b_d$ -convergent to x and denote it by $x_n\to x$ as $n\to \infty$ .

The limit of a $b_d$ -convergent sequence in a $b_d$ -metric space is unique ( [15] , Proposition 1.27).

Definition 2.6 [15] A sequence $\left\{x_n\right\}$ in a $b_d$ -metric space $\left(X,b_d\right)$ is called a $b_d$ -Cauchy sequence if, given $\epsilon >0$ , there exists $n_0\in N$ such that for all $n,m>n_0$ , we have $b_d\left(x_n,x_m\right)<\epsilon$ or $\underset{n,m\to \infty }{\lim }{b}_d\left(x_n,x_m\right)=0$ . Every $b_d$ -convergent sequence in a $b_d$ -metric space is a $b_d$ -Cauchy sequence.

Remark 2.7 The sequence $\left\{x_n\right\}$ in a $b_d$ -metric space $\left(X,b_d\right)$ is called a $b_d$ -Cauchy sequence if $\underset{n,m\to \infty }{\lim }{b}_d\left(x_n,x_{n+p}\right)=0$ for all $p\in N^{\ast }$ .

Definition 2.8 [15] A $b_d$ -metric space $\left(X,b_d\right)$ is called complete if every $b_d$ -Cauchy sequence in X is $b_d$ -convergent.

Example 2.9 If $X=R^{+}\cup \left\{0\right\}$ , then $b_d\left(x,y\right)={\left(x+y\right)}^2$ defines a b-dislocated metric on X with parameter $s=2$ .

Example 2.10 Let $X=R^{+}\cup \left\{0\right\}$ and any constant $\alpha >0$ . Define function $d_l:X\times X\to R^{+}$ by $d_l\left(x,y\right)=\alpha \left(x+y\right)$ . Then, the pair $\left(X,d_l\right)$ is a dislocated metric space.

If $Fx=Sx$ for some $x\in X$ , then x is called the coincidence point of F and S. Furthermore, if the mappings commute at each coincidence point, then such mappings are called weakly compatible [4] .

Definition 2.11 [17] The altering distances functions $\psi$ and $\phi$ are defined as

$\Psi =\left\{\psi :\left[0,\infty \right)\to \left[0,\infty \right)/\psi \text{is}\text{continuous},\text{nondecreasing},\text{and}\psi \left(t\right)=0\text{if}t=0\right\}$

$\Phi =\left\{\varphi :\left[0,\infty \right)\to \left[0,\infty \right)/\varphi \text{is}\text{lower}\text{semicontinuous},\text{and}\varphi \left(t\right)=0\text{if}t=0\right\}$

The following lemmas are used to prove our results.

Lemma 2.12 Let $\left(X,b_d\right)$ be a b-dislocated metric space with parameter $s\ge 1$ . Then

1) If $b_d\left(x,y\right)=0$ then $b_d\left(x,x\right)=b_d\left(y,y\right)=0$ ;

2) If $\left(x_n\right)$ is a sequence such that $\underset{n\to \infty }{\lim }{b}_d\left(x_n,x_{n+1}\right)=0$ , then we have

$\underset{n\to \infty }{\lim }{b}_d\left(x_n,x_n\right)=\underset{n\to \infty }{\lim }{b}_d\left(x_{n+1},x_{n+1}\right)=0$ ;

3) If $x\ne y$ , then $b_d\left(x,y\right)>0$ ;

Proof. It is clear.

Lemma 2.13 [15] Let $\left(X,b_d\right)$ be a b-dislocated metric space with parameter $s\ge 1$ . Suppose that $\left\{x_n\right\}$ and $\left\{y_n\right\}$ are $b_d$ -convergent to $x,y\in X$ , respectively. Then we have

$\frac{1}{s^2}{b}_d\left(x,y\right)\le \underset{n\to \infty }{\lim }\inf b_d\left(x_n,y_n\right)\le \underset{n\to \infty }{\lim }\sup b_d\left(x_n,y_n\right)\le s^2{b}_d\left(x,y\right)$

In particular, if $b_d\left(x,y\right)=0$ , then we have $\underset{n\to \infty }{\lim }{b}_d\left(x_n,y_n\right)=0=b_d\left(x,y\right)$ . Moreover, for each $z\in X$ , we have

$\frac{1}{s}{b}_d\left(x,z\right)\le \underset{n\to \infty }{\lim }\inf b_d\left(x_n,z\right)\le \underset{n\to \infty }{\lim }\sup b_d\left(x_n,z\right)\le s{b}_d\left(x,z\right)$

In particular, if $b_d\left(x,z\right)=0$ , then we have $\underset{n\to \infty }{\lim }{b}_d\left(x_n,z\right)=0=b_d\left(x,z\right)$ .

Definition 2.14. [24] [25] We say that a function $f:{\left[0,\infty \right)}^2\to R$ is called a C-class function if it is continuous and satisfies the following properties.

$\begin{array}{l}1)f\left(s,t\right)\le s\\ 2)f\left(s,t\right)=s\Rightarrow s=0\text{or}t=0\text{for}\text{all}s,t\in \left[0,\infty \right)\\ \text{3)}f\left(0,0\right)=0\end{array}$

We denote C-class functions as C.

Example 2.15 [24] [25] The following functions $f:{\left[0,\infty \right)}^2\to R$ are elements of C, for all $s,t\in \left[0,\infty \right)$ :

1) $f\left(s,t\right)=s-t,f\left(s,t\right)=s\Rightarrow t=0$

2) $f\left(s,t\right)=\frac{s-t}{1+t},f\left(s,t\right)=s\Rightarrow t=0$

3) $f\left(s,t\right)=\frac{st}{1+t},f\left(s,t\right)=s\Rightarrow s=0$

4) $f\left(s,t\right)=\frac{s}{1+t},f\left(s,t\right)=s\Rightarrow s=0\text{or}t=0$

5) $f\left(s,t\right)=\log \frac{t+a^s}{1+t},a>\text{1,}f\left(s,t\right)=s\Rightarrow s=0\text{or}t=0$

For $t=1$ , we have $f\left(s,1\right)=\ln \frac{1+a^s}{2},a>e,f\left(s,1\right)=s\Rightarrow s=0$

6) $f\left(s,t\right)={\left(s+k\right)}^{\frac{1}{1+t}}-k,k>1,f\left(s,t\right)=s\Rightarrow t=0$

7) $f\left(s,t\right)=s{\log }_{a+t}a,a>1,f\left(s,t\right)=s\Rightarrow s=0\text{or}t=0$

8) $f\left(s,t\right)=ms,0<m<1;f\left(s,t\right)=s\Rightarrow s=0$

9) $f\left(s,t\right)=\varphi \left(s\right),f\left(s,t\right)=s\Rightarrow s=0$ , here $\varphi :\left[0,\infty \right)\to \left[0,\infty \right)$ is continuous and such that $\varphi \left(0\right)=0$ and $\varphi \left(t\right)<t$ for $t>0$ .

3. Main Results

Before we give the main result we denote with letter the following set

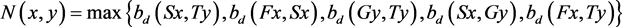(3.1.1)

for all.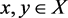

Motivated by the works of [15] [21] - [29] we extend the concept of 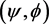-weakly contractive maps to four maps in a b-dislocated metric space, giving the following definition.

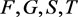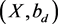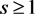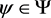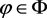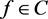Definition 3.1 Let be four self maps of a b-dislocated metric space with parameter. If there exists, and such that

(A)

for all, where 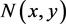is defined as in (3.1.1) then and T are said to satisfy a generalized 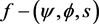weakly contractive condition.

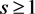Theorem 3.2 Let be a b-dislocated metric space with parameter and 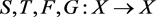are self-mappings such that (a), and satisfy generalized weakly contractive condition. If one of or is a complete subspace of X, then and have a point of coincidence in X. Moreover if suppose that and are weakly compatible pairs, then have a unique common fixed point.

Proof. Let be an arbitrary point in X. Since we can choose such that. And since corresponding to we can choose such that. Continuing the same process we obtain sequences and in X such that:

for all

We consider following steps:

Step 1. If (that means) for some n, then. Hence is a coincidence point of G and T. Using definition of and lemma 2.12 we have,

Thus (3.2.1)

Using condition (A) and property of C-class, we have that

By property of we have,

(3.2.2)

As a result we get,

.

Again from contractive condition of theorem have,

The inequality above implies,

By property of function f of C-class we obtain

or.

And also by property of we get so that and then. Also is a coincidence point of F and S.

Step 2. Suppose that means for all n by condition (3.1.1) we have:

If then (3.2.3)

Also from condition of theorem we have:

By property of function we have

(3.2.4)

From (3.2.3) and (3.2.4) we get

(3.2.5)

Also from condition of theorem and (3.2.5) we have,

The above inequality implies:

which means

.

From property of C-class we obtain

.

So we have that is a contradiction since we suppose.

So we have.

In a similar way as above we have. As a result

the sequence is non increasing and bounded below. And so there exists such that,

.

Suppose that. Since is continuous and is lower semi continuous we have:

(3.2.6)

If we consider condition (A) we have,

(3.2.7)

taking the upper limit as in (3.2.7) and using (3.2.6) we have that,

(3.2.8)

From (3.2.8) and property of we get that is a contradiction. Hence

(3.2.9)

Now we prove that is a -Cauchy sequence. Assume the contrary that is not a -Cauchy sequence. Then there exists for which we can

find subsequences and of so that is the smallest index for which, that

(3.1.10)

and (3.2.11)

From property c) of definition 2.2 we have:

(3.2.12)

Taking the upper limit as in (3.2.12) and using result (3.129) and (3.2.11), we get

(3.2.13)

Also we have

(3.2.14)

Hence taking the upper limit in above inequality, we obtain

(3.2.15)

Again from property c) of definition 2.2, we have

(3.2.16)

Thus from 3.2.9; 3.2.15 we have

(3.2.17)

As a result,

(3.2.18)

Similarly,

(3.2.19)

Taking the upper limit in (3.2.19) and using 3.2.9, we get

(3.2.20)

Similarly,

Taking the upper limit in above inequality and using (3.2.9), we have

(3.2.21)

Also,

Taking the upper limit and using 3.2.9; 3.2.18 we get

(3.2.22)

So, by (3.2.21) and (3.2.22) we have

(3.2.23)

According to the set (3.1.1) we have:

(3.2.24)

Taking the upper limit in (3.2.24) and using results 3.2.9; 3.2.18; 3.2.13; 3.2.23 we get

(3.2.25)

Similarly, we can show,

(3.2.26)

From contractive condition of theorem, we have

(3.2.27)

Taking the upper limit as in (3.2.27) and using 3.2.25; 3.2.26, we obtain

From this inequality and since is non decreasing follows that

.

That is a contradiction since we supposed. Thus is a -Cauchy sequence in b-dislocated metric space. Also the subsequences, , , are -Cauchy. Let we suppose that is a complete subspace of X, since the subsequence is -Cauchy then there exists such that. Then we have,

. (3.2.28)

Since, then there exists such that. According to (3.1.1) consider

(3.2.29)

Taking the upper limit and using lemma 2.13, result (3.2.9) and (3.2.28) we obtain

(3.2.30)

Using contractive condition (A) of theorem we have,

(3.2.31)

Taking the upper limit in (3.2.31) and using (3.2.30) we get

This implies and so. Thus, so y is a point of coincidence of the pair.

Similarly we can show that, so v is a point of coincidence of the pair. Therefore we have

. (3.2.32)

Let show that z is a unique point of coincidence of pairs and. Suppose that exists another point such that.

We consider,

Using contractive condition of theorem we have,

The inequality above implies that so that means the point of coincidence is unique.

Let prove that z is a common fixed point. By the weak compatibility of the pairs and have: and.

From condition of theorem we have,

(3.2.33)

This inequality implies.

And

(3.2.34)

Again from (3.2.33) and (3.2.34) we get,.

By property of functions and C-class, we have

(3.2.35)

So we obtained, that iz. Therefore.

Let we prove that z is a fixed point of F.

Again we consider

By property of follows

(3.2.36)

where

(3.2.37)

From (3.2.36), (3.2.37) we get

(3.2.38)

In similar way as in (3.2.35) using (3.2.38), property of C-class and functions we obtain, and. Hence z is a common fixed point.

Uniqueness. Let we prove that the fixed point is unique. If suppose that u and z are two common fixed points of F, G, S, T then from condition (b) we have,

By property of we get. Also we have,

So,

and

As a result and so.

The following is corollary of theorem 3.2 which is taken for parameter in a dislocated metric space.

Corollary 3.3 Let be a dislocated metric space and are self-mappings such that (a), and exists, and such that satisfy the condition

(A)

for all, where is defined as in (3.1.0). If one of or is a complete subspace of X, then and have a point of coincidence in X. Moreover if suppose that and are weakly compatible pairs, then have a unique common fixed point.

Now we give an example to support our Theorem 3.2.

Example 3.4 Let and. Then the pair

is a b-dislocated metric space with parameter. We define the functions

and T as follows:. The pairs

and are weakly compatible, functions and T are continuous and

We have,

where; and, for all.

Thus all conditions of theorem 3.2 are satisfied and is the unique common fixed point of and G.

In a similar way as in Theorem 3.2, the following theorem can be proved.

Theorem 3.5 Let be a complete b-dislocated metric space with parameter and are self-mappings such that (a) and satisfy generalized weakly contractive condition. If one of or is closed, then and have a point of coincidence in X. Moreover if suppose that and are weakly compatible pairs, then have a unique common fixed point.

For the different functions f of C-class (refer to example 2.15) we can take the following corollaries.

Corollary 3.6 Let be a -dislocated metric space with parameter and are self-mappings where (a) and exists, such that satisfies the condition

for all, where is defined as in (3.1.0). If one of or is a complete subspace of X, then and have a point of coincidence in X. Moreover if suppose that and are weakly compatible pairs, then have a unique common fixed point.

Proof. If we take in Theorem 3.2 the function f as then we get the corollary.

Corollary 3.7 Let be a -dislocated metric space with parameter and are self-mappings where (a) and exists, such that satisfies the condition

for all, where is defined as in (3.1.0). If one of or is a complete subspace of X, then and have a point of coincidence in X. Moreover if suppose that and are weakly compatible pairs, then have a unique common fixed point.

Proof. This corollary is obtained from Theorem 3.2 if we take as f the function

.

Corollary 3.8 Let be a -dislocated metric space with parameter and are self-mappings where (a) and exists, such that satisfies the condition

for all, where is defined as in (3.1.0). If one of or is a complete subspace of X, then and have a point of coincidence in X. Moreover if suppose that and are weakly compatible pairs, then have a unique common fixed point.

Proof. If we take in Theorem 3.2 the function f as then we get the corollary.

Corollary 3.9 Let be a -dislocated metric space with parameter and are self-mappings where (a) and exists, such that satisfies the condition

for all, where is defined as in (3.1.0). If one of or is a complete subspace of X, then and have a point of coincidence in X. Moreover if suppose that and are weakly compatible pairs, then have a unique common fixed point.

Proof. If we take in Theorem 3.2 the function f as then we get the corollary.

Remark 3.10 As a consequence of theorem 3.2 and all corollaries for taking

1) the parameter.

2) the parameter and and.

3) functions f from the set C and taking and.

We can establish many other corollaries in the setting of dislocated and b-dislocated metric spaces.

4) Our results unify, generalize, and extend several ones obtained earlier in a lot of papers concerning b-metric, dislocated and b-dislocated metric spaces (as in references [13] [15] [25] [26] [30] [31] ).

In this section, we use the notion of T-contractions introduced by Beiranvad et al. in [3] as a new class of contractive mappings, by generalizing the contractive condition in terms of another function. These contractions have been used by many authors. In this direction in order to generalize some other well-known results as in [32] [33] [34] we extend the notion of generalized weak contractions in the context of T-contractions, giving the following theorem.

Theorem 3.11 Let be a complete b-dislocated metric space with parameter and be an injective, continuous and sequentially convergent mapping. Let be self-mappings and if exist, and such that

(B)

for all, where

then have a unique common fixed point.

Proof. We divide the proof into two parts as follows.

First part. Each fixed point u of F is a fixed point of G and conversely, and the common fixed point of is unique.

Let be a fixed point of F. If then, follows that and so u is a fixed point of G. If we suppose that, we evaluate as;

So we have

(3.11.1)

Then by contractive condition (B), we have

By property of we have

(3.11.2)

Hence from (3.11.1) and (3.11.2) follows.

Again

By property of we get that is and by injectivity of T follows.

Thus u is a fixed point of G. Similarly we can prove the other implication.

Second part. We prove that the function F has a fixed point. We define two eterative sequences as and, and as for each.

If for some n, we have then and is a fixed point of F and by the first part is a fixed point of G and the proof is completed.

Now, we assume that for all n, and since T is injective we have; then from condition (B) of theorem, we have

where

(3.11.3)

If then from (3.11.3) we get

(3.11.4)

Using condition (B) and property of C-class, we have

By property of function we have

(3.11.5)

From (3.11.4) and (3.11.5) we get

(3.11.6)

Also from condition of theorem and (3.11.6), we have

Also we have,

By property of and we have so which is a contradiction since we supposed.

Hence, we have

.

Similarly, we have that

Therefore for all n we have

and is a non increasing sequence of nonnegative real numbers

and bounded below. Hence there exists such that

By the property of functions and, we have

(3.11.7)

If we consider condition (B) we have,

(3.11.8)

Taking the upper limit as in (3.11.8) and using (3.11.7) we have that,

(3.11.9)

From (3.11.9) and property of and follows that and also

(3.11.10)

In a similar way as in Theorem 3.2 we can show that the sequence (also) is a -Cauchy sequence in b-dislocated metric space. Since X is complete there exists such that. Since T is sequentially convergent, we can deduce that is convergent to and the subsequences converge to u, that means

.

Since T is continuous we have.

Let we prove that u is a fixed point of F and G (). If suppose that then since T is injective follows (and)

Consider,

(3.11.11)

Taking the upper limit in (3.11.11) and using lemma (2.13), and result (3.11.10) we get

(3.11.12)

According to contractive condition (B) we have,

(3.11.13)

Taking the upper limit in (3.11.13) and using lemma (2.13), we obtain,

This implies that that is which is a contradiction. As a result and u is a fixed point of F. By the first part of proof u is a fixed point of G and also a common fixed point.

Easily using the contractive condition (B) of theorem can be proved that the common fixed point is unique.

Example 3.12 Let be equipped with the b-dislocated metric

for all, where. It is clear that is a complete b-dislocated metric space. Also let be the self-mappings

defined by. We note, T is continuous and sequentially convergent.

If, and then for each, we have

Thus satisfy all the conditions of Theorem 3.11. Moreover is the unique common fixed point of.

If in theorem3.11 we take we get the following corollary.

Corollary 3.13 Let be a complete b-dislocated metric space with parameter and be two self mappings, where T is injective, continuous and sequentially convergent. If exist, and such that

for all, where

then G has a unique fixed point.

Corollary 3.14 Let be a complete b-dislocated metric space with parameter and be an injective, continuous and sequentially convergent mapping. Let be self-mappings and if exist, such that

for all, where

then have a unique common fixed point.

Proof. If we take in Theorem 3.11 the function as then we get the corollary.

Remark 3.15

1) Theorem 3.11 generalizes, extends and unifies results as Theorem 8 in [32] , Theorem 4 in [33] and many existing results of literature in a set effective larger as b-dislocated metric spaces.

2) The class C of functions has a general character and so according to example 2.15, we can provide many results from theorem 3.11.

3) If we take in theorem 3.11 the parameter as a consequence, we obtain results in a dislocated metric space.

Cite this paper

Dine, J., Zoto, K. and Ansari, A.H. (2018) Fixed Point Results of Contractive Mappings by Altering Distances and C-Class Functions in b-Dislocated Metric Spaces. Open Access Library Journal, 5: e4657. https://doi.org/10.4236/oalib.1104657

References