 Wireless Sensor Network, 2009, 1, 358-364 doi:10.4236/wsn.2009.14044 Published Online November 2009 (http://www.scirp.org/journal/wsn). Copyright © 2009 SciRes. WSN An Energy-Efficient MAC Protocol for WSNs: Game-Theoretic Constraint Optimization with Multiple Objectives Liqiang ZHAO, Le GUO, Li CONG, Hailin ZHANG State Key Laboratory of Integrated Services Networks, Xidian University, Xi’an, China Email: lqzhao@mail.xidian.edu.cn Received March 23, 2009; revised June 2, 2009; accepted June 10, 2009 Abstract In WSNs, energy conservation is the primary goal, while throughput and delay are less important. This re- sults in a tradeoff between performance (e.g., throughput, delay, jitter, and packet-loss-rate) and energy con- sumption. In this paper, the problem of energy-efficient MAC protocols in WSNs is modeled as a game-theoretic constraint optimization with multiple objectives. After introducing incompletely cooperative game theory, based on the estimated game state (e.g., the number of competing nodes), each node independ- ently implements the optimal equilibrium strategy under the given constraints (e.g., the used energy and QoS requirements). Moreover, a simplified game-theoretic constraint optimization scheme (G-ConOpt) is pre- sented in this paper, which is easy to be implemented in current WSNs. Simulation results show that G-ConOpt can increase system performance while still maintaining reasonable energy consumption. Keywords: Wireless Sensor Network, MAC, Energy Efficiency, Game Theory, Constraint Optimization 1. Introduction As an emerging technology, Wireless Sensor Networks (WSNs) have a wide range of potential applications in- cluding environment monitoring, smart spaces, medical systems and robotic exploration. Performance analysis and optimization of WSNs, especially its Medium Access Control (MAC) protocols, have attracted much research interests. Traditional MAC protocols for wireless ad hoc networks are designed to maximize throughput and minimize delay. As sensor nodes are generally bat- tery-operated, to design a good MAC protocol for WSNs, the first attribute that has to be considered is energy con- sumption [1]. Other important attributes (such as throughput and delay) are generally the primary concerns in traditional wireless ad hoc networks, but in WSNs they are secondary. IEEE 802.11 Distributed Coordination Function (DCF), the basic MAC protocol in Wireless LANs (WLANs), is based on Carrier Sense Multiple Access with Collision Avoidance (CSMA/CA), one of typical contention-based MAC protocols. CSMA/CA uses an acknowledgment (ACK) mechanism for verifying successful transmissions and optionally, an RTS/CTS handshaking mechanism for decreasing collisions overhead. In both cases an exponen- tial backoff mechanism is used. Before transmitting, a node generates a random slotted backoff interval, and the number of the backoff slots is uniformly chosen in the range [0, CW-1]. At the first transmission attempt, the contention window, CW, is set equal to a value CWmin called the minimum contention window. After each un- successful transmission, CW is doubled up to the maxi- mum value CW max. Once CW reaches CWmax, it will re- main at the value until the packet is transmitted success- fully or the retransmission time reaches retry limit. While the limit is reached, retransmission attempts will cease and the packet will be discarded. Currently, CSMA/CA has been the de facto MAC standard for wireless ad hoc networks, widely used in almost all of the testbeds. Moreover, low-power, low-rate Wireless PANs (WPANs) such as IEEE 802.15.4 utilizes CSMA/CA too. However, the energy consumption using CSMA/CA is very high when nodes are in an idle mode. It is mainly called prob- lem of idle listening. CSMA/CA-based S-MAC is explic- itly designed for WSNs to solve this problem [2]. The basic idea of S-MAC is that used energy is traded for throughput and delay by introducing an active/sleep duty period. Some researchers are attempting to improve the performance of S-MAC [3–6]. To handle load variations in time and location, T-MAC introduces an adaptive duty cycle by dynamically ending its active part. This reduces  L. Q. ZHAO ET AL. 359 the amount of energy wasted on idle listening, in which nodes wait for potentially incoming messages, while still maintaining a reasonable throughput [7]. Recently, game theory [8] becomes a very good tool to analyze and improve the performance of contention-based protocols. Game-theoretic approaches were proposed to solve the problem of security, query routing, and power control respectively in distributed sensor networks [9–12]. When using game theory in WSNs rather than mathe- matics or economics, much attention should be paid to the context of WSNs. For example, explicit cooperation among nodes is clearly impractical in WSNs as it causes additional energy and bandwidth consumption. We pre- sented a novel concept of incompletely cooperative game theory to improve the performance of MAC protocols in WSNs without any explicit cooperation among nodes [13–14]. In this paper, the preliminary results presented in [13–14] will be substantially extended. The problem of energy-efficient MAC protocols for WSNs is modeled as game-theoretic constraint optimization with multiple ob- jectives, e.g., energy consumption and QoS metrics. 2. Game-Theoretic Constraint Optimization A node starts a game process when a new packet arrives at the node’s transmission buffer and ends it when the packet is moved out of the buffer (i.e., transmitted suc- cessfully or discarded). Each game process includes many time slots and each time slot corresponds to one game state. In each time slot, each player (i.e., node) estimates the current game state based on its history. After estimat- ing the game state, the player adjusts its own equilibrium strategy by tuning its local contention parameters. Then all the nodes take actions simultaneously, i.e., transmit- ting, listening, or sleeping. Although the player does not know which action the other nodes (i.e., its opponents) are taking now, it can predict its opponents’ actions ac- cording to its history. In the game, each player takes a distributed approach of detecting and estimating the current game state, and tun- ing its local contention parameters to the estimated game state. In economics, normally, the optimal target of the player is to maximum its own profits. However, in WSNs, the target of each player is to maximum the system per- formance under certain limits, e.g., energy consumption and QoS requirements. In the game for WSNs, the utility function of the player (i.e., node i) is represented by , iiii sμμ . The pa- rameters of the vector, μi,j correspond to its energy con- sumption and QoS requirements, e.g., bandwidth, delay, jitter, and packet-loss-rate. Obviously, there are some limits on its utility function, called max i , e.g., the maxi- mum energy consumption, the tolerant minimum band- width, maximum delay, jitter, or packet-loss-rate. If we do not consider its opponents, the strategy of the player, si, includes three possible actions: transmitting, listening or sleeping. The strategy profile of its opponents (i.e., all the other n neighbors) is defined as 121 1 , ,...,,,..., iiin sss ss . Similarly, we can get the utility function of its opponents that , iiii μ s . Also, there are some limits on the above utility function, called max i μ. In many game-theoretic models, a player is a node con- tending for the channel. As there may be many nodes in a WSN and each node may contend for the channel repeat- edly, a very complicated method is needed to determine the strategy. Hence, in the game, a player is not always a node. If we analyze the equilibrium strategy of node i, Player 1 is node i, and Player 2 (i.e., its opponents) is all the other n-1 nodes. In fact, it is possible for Player 1 to estimate Player 2’s state, and difficult for Player 1 to es- timate the states of each node in Player 2. In a formal description, we are looking for * ,, *m * , * ,, *m * , arg min arg min i i ij ij ii sjij ij ij ii sjij s s μμ μμ ax ax i i (1) Obviously, Player 1 adjusts its strategy si not to obtain its own optimal utility (), but to help Player 2 get the optimal utility ( * i μ * i ); vice verse. Hence, it indicates that all the nodes play the cooperative game based on the esti- mated game states. On the other hand, the two players help each other get the optimal utility under their own limits respectively. It indicates that all the nodes play the constrained game. As Player 2 includes all the other n-1 competing nodes except Player 1, collisions may happen among the n-1 competing nodes even not considering Player 1. So Player 2 includes four possible actions: successful transmission, failed transmission, listening or sleeping, even if we do not consider Player 1. Table 1 is the strategy table with 2 players (i.e., n nodes). With regard to the payoff of Play 1 in a given time slot, there are four possibilities when considering the two players. Firstly, Player 1 sleeps with the probability of , whose payoff is , where j corresponds to the j-th parameter of the utility function. Secondly, Player 1 listens to the channel with the probability of i w,wj c 11 i wi , whose payoff is . Here ,ij ci is the con- ditional transmission probability of Player 1. Thirdly, Player 1 fails to transmit its packets due to the collision etween the two players with the probability of b Copyright © 2009 SciRes. WSN  360 L. Q. ZHAO ET AL. Copyright © 2009 SciRes. WSN Table 1. Strategy model with n+1 nodes. ii cc , si cc , fi cc , is cc , ff cc , Transmitting Playe / ponent (all the other n nodes) Player 1 (node i) Listening Sleeping Sleeping ww cc , Listening Failed Transmission Successful Tran smission fw cc , iw cc , wi cc, wf cc , 11 ii ii www i , whose payoff is , j c. Here i w and i are the sleeping probability and the conditional transmission probability of Player 2 respectively. Finally, Player 1 transmits successfully with the probability of 111 ii ii ww ets due to the collisions between the two players or among the n-1 nodes within Player 2 with the probability of 11 11 iiii iiii wwpw w , whose payoff is ,fj c. Finally, Player 2 transmits successfully with the probability of 1111 ii iii wpw , whose payoff is , j c. Here, i p is the conditional colli- sion probability of Player 2, which is the function of the probability i [14]. , whose payoff is , j c. With regard to the payoff of Player 2 in a given time slot, there are four possibilities too after considering the two players. Firstly, Player 2 sleeps with the probability of i w, whose payoff is ,wj c Secondly, Player 2 listens to the channel with the probability of . 1 i 1 i w e payoff is , whos ,ij c. Thly, Player 2 fails to transmit its pack- Hence, the optimal strategies of the two players under the given constraints are expressed as ird ,, , *max * ,, ,, ,, *max * ,, 111111 11 arg min1 111 11 arg min1 ii ii iiijii iisji iiiiiifjiwj iii wjij iiiisjiijiii ifjiwj iii wjij wc pwcwpwwcwc s wwcc wwcwc s μμ μμ , ided into super-frames and every super-frame has two parts: an active part and a sle where τ is the frame transmission prob If solving the above equation w (2) In general, the contention-based MAC protocol in WSNs is modelled as a game-theoretic constraint optimi- zation with multiple objectives. Based on the estimated game state, each node achieves the global optima by ad- justing its transmission and sleeping probability simulta- neously. eping part. During the active part, each node contends for the channel in the incompletely cooperative game. During the sleeping part, each node turns off its radio to preserve energy. The time length of the active and sleep- ing part is adjusted according to the estimated game state too. In the game, firstly, a node estimates the current state of the game, e.g., the number of its opponents n-1. When th 3. A Simplified Game-Theoretic Constraint Optimization Scheme for WSNs e node is transmitting its frame, if any other node transmits at the same time slot, the frame will be collided. So the frame collision probability of the node p is ob- tained as follows: 1 11 n p (3) Unfortunately, the above problem has been proven to be NP-hard [15], so we cannot hope an algorithm that can find the theoretical optimum and runs in polynomial time. Hence, we present a simplified game-theoretic constraint optimization scheme (G-ConOpt) in this section. In G-ConOpt, we optimize the performance (e.g., the system throughput, delay, jitter, and packet-loss-rate) under the limited energy consumption. In G-ConOpt, time is div ability of the node. ith respect to n, we ob- tain: log 1 1p nlog 1 (4) 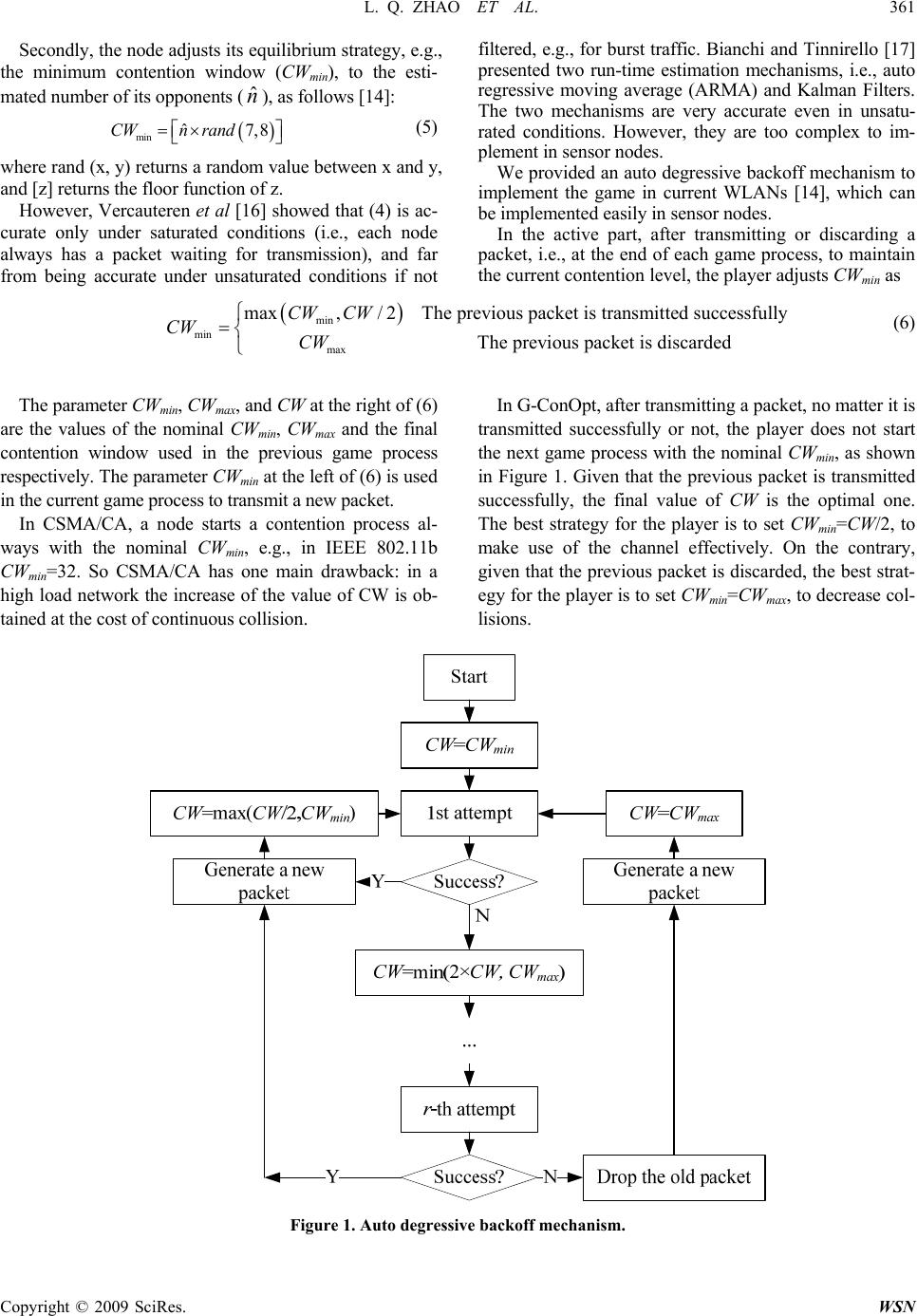 L. Q. ZHAO ET AL. 361 Secondly, the node adjusts its e.g the minimum contention windomin m quilibrium strategy, e., w (CW ), to the esti- ated number of its opponents (ˆ n), as follows [14]: min ˆ7,8CWn rand (5) where rand (x, y) returns a rando value between x amnd y, and [z] returns the floor function of z . However, Vercauteren et al [16] showed that (4) is ac- curate only under saturated conditions (i.e., each node always has a packet waiting for transmission), and far from being accurate under unsaturated conditions if not filtered, e.g., for burst traffic. Bianchi and Tinnirello [17] presented two run-time estimation mechanisms, i.e., auto regressive moving average (ARMA) and Kalman Filters. The two mechanisms are very accurate even in unsatu- rated conditions. However, they are too complex to im- plement in sensor nodes. We provided an auto degressive backoff mechanism to implement the game in current WLANs [14], which can be implemented easily in sensor nodes. In the active part, after transmitting or discarding a packet, i.e., at the end of each game process, to maintain the current contention level, the player adjusts CWmin as min min max,/2The prevCW CW CW CW max ious packet is transmitted successfully The previous packet is discarded (6) The parameter CWmin, CWmax, and CW at the right of (6) re the values of the nominal CWmin, CWmax and the final o s In G-ConOpt, after transmitting a packet, no matter it is transmitted successfully or not, the player does not start th a c ntention window ued in the previous game process respectively. The parameter CWmin at the left of (6) is used in the current game process to transmit a new packet. In CSMA/CA, a node starts a contention process al- ways with the nominal CW min, e.g., in IEEE 802.11b CWmin=32. So CSMA/CA has one main drawback: in a high load network the increase of the value of CW is ob- tained at the cost of continuous collision. e next game process with the nominal CWmin, as shown in Figure 1. Given that the previous packet is transmitted successfully, the final value of CW is the optimal one. The best strategy for the player is to set CWmin=CW/2, to make use of the channel effectively. On the contrary, given that the previous packet is discarded, the best strat- egy for the player is to set CWmin=CWmax, to decrease col- lisions. Figure 1. Auto degressive backoff mechanism. Copyright © 2009 SciRes. WSN  362 L. Q. ZHAO ET AL. Obviously, compared with the gam ve feature of G-ConOpt is that it is simple to implement. i Moreover, at the end of the active part, the node of the active part (Tactive) and the next pe e, the most attrac-ergy consumption. ti Frstly, no estimation mechanism is needed. Secondly, it is not needed to compute the optimal value of CWmin. That is to say, G-ConOpt would not cause any more en- changes the length riod (Tnext), according to the estimated game state, as follows: ,min 0. ˆ min,2, /0.1 active nextcurrentcurrentcurrent current activeactive activenextactive next active act TT TTTnnTT TT currentnext current ivesleep sleep TT else ,max max , next current activeactive activenext TTTT ˆ 5, /0.5 currentcurrent current TnnTT (7) where max(x, y) and min(x, y) return the larger value and e smaller value between x and y respectively. The pa- an that in the last ac rotocol G-ConOpt, the fol- wing simulations are made in an ideal channel. The channel rate aSlot Time retry limit MAC PHY header The packets will be discarded only due to the re- transmission time reaches the retry limit, and do not coe dt.ary withe cooor anvices, where eacnerates n sizs under a Poocess and tr th rameters current active T and current T are the time length of the active part and the period in the current period. Tactive,max and Tactive, the m and minimum length of the active part. next active T and next T are used in the next period. α is a predetermined integer, n is the last esti- mated number of eting n, and ˆ n is the current estimated number of competing nodes. At the end of the current active part, if the estimated number of competing nodes is larger th min, areaximum p ocomdes tive part, it indicates many nodes still have packets to send. So the time length of the next active part equals to that of the current active part plus α but not longer than the maximum active part size. The time length of the next period is half that of the current period; thereby the nodes can wake up more frequently to reduce the delay of communication. On the other hand, if the estimated num- ber of competing nodes is smaller than that in the last period, the time length of the next active part equals to that of the current active part minus α but not shorter than the minimum active part size. The time length of the next period is twice that of the current period, so the nodes need not wake up frequently. 4. Simulation Results To evaluate the proposed p lo values of the parameters used to obtain numerical results for simulations are specified in IEEE 802.11b protocol, as shown in Table 2. Table 2. Simulation parameters. header 1Mb/s 20μs 7 144μs 192μs ACK SIFS nsider th rdinat elay limi d 50 de We set a st topolog h device ge on ew fixed a e packetisson pr nsmit them to the coordinator. The packet arrival rate is initially set to be lower than the saturation case, and it is subsequently increased so that, at the end of the simu- lation time, all nodes are almost in saturation conditions [18]. CSMA/CA is considered as the worst case: it has no energy saving features at all. The radio of each node does not go into the sleep mode. It is either in the listen- ing/receiving mode or transmitting mode. S-MAC is con- sidered as the basic contention-based MAC protocol in WSNs. It includes the periodic active and sleeping time to achieve energy savings. For simplicity, the length of the active and sleeping part are fixed at 500ms in the follow- ing simulations. Compared with S-MAC, T-MAC can adapt to the load variations in time and location, and can end the active part according to the traffic loads. Figure 2 shows that the four protocols have almost the same system throughput under light traffic loads, and under heavy traffic loads, the system throughput of G-ConOpt is a little higher than that of CSMA/CA, which is about 2 times that of S-MAC and a little higher than T-MAC. 0 2040608010012014016018 0.0 0.1 0.2 0.3 0.4 0.5 0.6 put G-ConOpt S-MAC T-MAC CSMA/CA DIFS 5 T Receiving Listen Power Sleeping Power 27.45mW 13.5mW 13.5mW 0.015mW CWmin CWmax 112μs 10μs 0μs 32 1024 ransmit Power Power System through Sim u la tio n time(sec) 0 Figure 2. System throughput. Copyright © 2009 SciRes. WSN  L. Q. ZHAO ET AL. 363 Figure 3 shows that delay in G-ConOpt, CSMA/CA and T-MAC are much lower than that in S-MAC. Under light traffic loads, delay in G-ConOpt is a little larger than that in CSMA/CA, which is due to the periodic active/ sleeping period in G-ConOpt. Under heavy traf- fic loads, delay in G-ConOpt is lower than that in CSMA/CA and T-MAC, which is due to the game in G-ConOpt. Figure 4 shows that jitter in S-MAC is much higher than that in the other 3 protocols. Figure 5 shows that packet-loss-rate in G-ConOpt al- most keeps zero, which is much lower than that in S- MAC and CSMA/CA. Meanwhile, packet-loss-rate in G- ConOpt is a little lower than that in T-MAC, which is du to the game in F s larger than that in S-MAC un C protocol, S-MAC has higher energy eff e G-ConOpt. igure 6 shows that the energy consumption in S-MAC is near to one half that in CSMA/CA, which is due to the periodic active/sleeping scheme. Energy con- sumption in T-MAC is a little lower than that in S-MAC under light traffic loads, for nodes in T-MAC sleep longer than that in S-MAC. However, energy consumption in T-MAC i der heavy traffic loads, since nodes in T-MAC sleep shorter than that in S-MAC. The energy consumption in G-ConOpt is the lowest one in the four protocols, which is due to the dynamic duty cycle strategy and the game in G-ConOpt. As an energy-efficient MAC protocol, G-ConOpt considers not only energy consumption but also energy efficiency (i.e., the ratio of the successfully transmitted bit rate to energy consumption). Figure 7 shows that energy efficiency in G-ConOpt is much higher than that in S-MAC and CSMA/CA and T-MAC. As an en- ergy-aware MA iciency than CSMA/CA under light traffic loads. However, the advantage of S-MAC over CSMA/CA decreases with the increasing of traffic loads. Under heavy traffic loads, energy efficiency in S-MAC is al- most equal to that in CSMA/CA. Energy efficiency in T-MAC is always larger than that in S-MAC and T-MAC. 020406080100 120 140 160 180 0 5 10 15 20 25 30 Delay(sec) Simulation time(sec) G-ConOpt S-MAC T-MAC CSMA/CA 020406080100 120 140 160 180 0 1 2 3 4 5 6 7 Jitter(s Simulation time(sec) ec) G-ConOpt S-MAC T-MAC CSMA/CA Figure 3. Delay. Figure 4. Jitter. 020406080100 120 140 160 180 0.0 00 0.0 05 0.0 10 0.0 15 0.0 20 0.0 25 0.0 30 0.0 35 Packet-loss-rate Simulation time(sec) G-ConOpt S-MAC T-MAC CSMA/CA 020406080100 120 140 160 180 0 10 30 40 50 60 20 Energ nsumption(mj) Simu la tio n tim e (s e c ) G-ConOpt S-MAC T-MA C y co CS MA/CA Figure 5. Packet-loss-rate. Figure 6. Energy consumption. Copyright © 2009 SciRes. WSN  364 L. Q. ZHAO ET AL. 020406080100 120 140 160 180 6 7 8 9 10 11 12 13 14 15 16 Energy efficiency(kb/s/mj) Si mu la tion time (s e c) G-ConOpt S-MAC T-MAC CSM A/CA Figu 5. Conclusions In this paper, firstly, the incompletely cooperative game is used to model the MAC protocol of WSNs. Secondly, after considering the context of WSNs, e.g., the require- ments on energy consumption, the problem of the MAC protocols of WSNs is modeled as a game-theoretic con- straint optimization problem. Moreover, one simple f mulation is presented for the problem. Finally, a simpli- fied protocol, G-ConOpt is proposed, which can be eas- ily implemented in current WSNs. Based on G-ConO each nodes can achieve independently the optimal per- formance under limited energy consumption. The sim lation results show that G-ConOpt is an appropriate too to improve ther certain con only provide a simplified meth ddress the sleeping probability. We are developing [3] efficient MAC protocol for wireless sensor networks,” ACM SenSys, Los Angeles CA, November 2003. [4] J. Polastre, J. Hill, and D. Celler, “Versatile low power media access for wireless sensor networks,” ACM SenSys, USA, pp. 95–107, November 2004. [5] A. El-Hoiydi and J. D. Decotignie, “WiseMAC: An ultra low power MAC protocol for the downlink of infrastructure wireless sensor networks,” ISCC, Egypt. pp. 244–251, June 2004. [6] P. Lin, C. Qiao, and X. Wang, “Medium access control with dynamic duty cycle for sensor networks,” WCNC, Atlanta, Georgia, March 2004. [7] T. van Dam, K. Langendoen, “A adaptive energy-efficient MAC protocol for wireless sensor networks,” ACM y,” The “Sensor-centric ed reliable query routing for wireless s,” Journal of Parallel and Distributed Computing, Vol. 64, No. 7, pp. 839–852, July 2004. 6. e . Zhang, “A Game- D. S. Johnson, “Computers and EEE 802.11 ysis of the IEEE 802.11 re 7. Energy efficiency. SenSys, USA, pp 171–180, November 2003. [8] P. D. Straffin, “Game theory and strateg or- pt, - [12] X. Zhang, Y. Cai, and H. Zhang, “A game-theoretic dynamic power management policy on wireless sensor network,” ICCT, China, pp. 1–4, November 200 u l - [ performance of WSNs unde straints. In this paper we od to an on Communication Systems, China, pp. 114–118, November 2008. [14] L. Zhao, L. Guo, J. Zhang, and H a analytical model to obtain the optimal equilibrium of the sleeping probability. Acknowledgement: This work is supported by the 111 Project (B08038), State Key Laboratory of Integrated Services Networks (ISN090105), Program for New Century Excellent Talents in University (NCET-08- 0810), National Natural Science Foundation of China (No. 60772137), and UK-China Science Bridges: R&D on 4G Wireless Mobile Communications. 6. References [1] I. F. Akyildiz, W. Su, Y. Sankarasubramaniam, et al., “Wireless sensor networks: a survey,” Computer net Networks, Vol. 38, No. 4, pp. 393–422, March 2002. [2] W. Ye, J. Heidemann, and D. Estrin, “An energy-efficient MAC protocol for wireless sensor networks,” INFOCOM, New York, Vol. 3, pp. 1567–1576, June 2002. T. Dam and K. Langendoen, “An adaptive energy- Mathematical Association of America, 1993. [9] A. Agah, S. K. Das, and K. A. Basu, “Game theory based approach for security in wireless sensor networks,” IPCCC, USA, pp. 259–263, April 2004. [10] R. Kannan, S. Sarangi, and S. S. Lyengar, energy-constrain sensor network [11] S. Sengupta and M. Chatterjee, “Distributed power control in sensor networks: A game theoretic approach,” IWDC, India, pp. 508–519, December 2004. 13] L. Zhao, L. Guo, K. Yang, and H. Zhang, “An Energy- efficient MAC Protocol for WSNs: Game-theoretic constraint optimization,” IEEE International Conferenc theoretic MAC protocol for wireless sensor network,” Journal of IET Communications, Vol. 3, No. 8, pp. 1274–1283, August 2008. [15] M. S. Garey and Intractability: Guide to the theory of NP-completeness,” W. H. Freeman, New York, 1979. [16] T. Vercauteren, A. L. Toledo, and X. Wang, “Batch and sequential bayesian estimators of the number of active terminals in an IEEE 802.11 network,” IEEE Trans. on Signal Processing, Vol. 55, No. 2, pp. 437–450, January 2007. [17] G. Bianchi and I. Tinnirello, “Kalman filter estimation of the number of competing terminals in an I work,” IEEE INFOCOM, Vol. 2, San Francisco, pp. 844–852, March 2003. [18] G. Bianchi, “Performance Anal distributed coordination function,” IEEE JSAC, Vol. 18, No. 3, pp. 535–547, March 2000. Copyright © 2009 SciRes. WSN
|