Paper Menu >>
Journal Menu >>
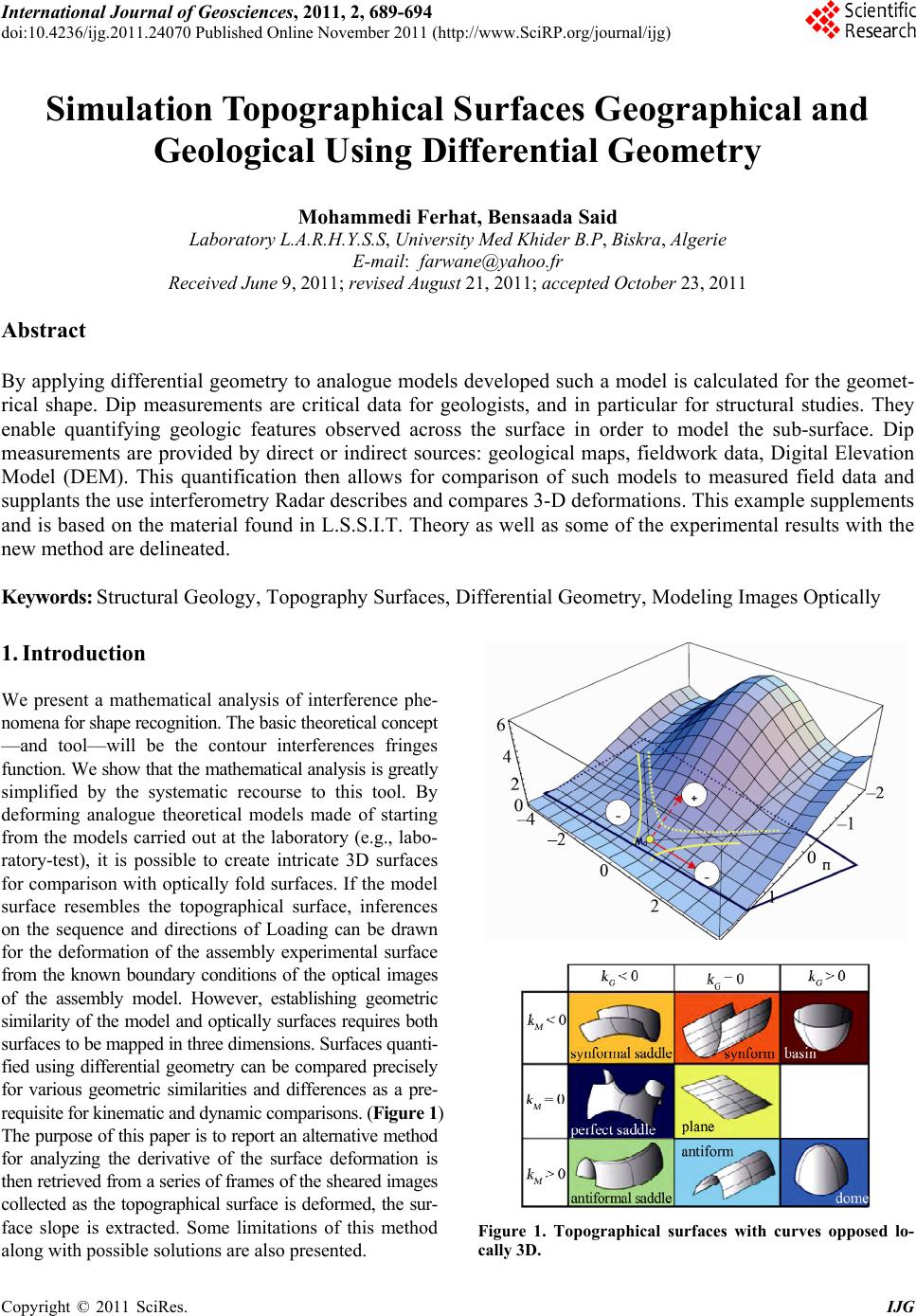 International Journal of Geosciences, 2011, 2, 689-694 doi:10.4236/ijg.2011.24070 Published Online November 2011 (http://www.SciRP.org/journal/ijg) Copyright © 2011 SciRes. IJG 689 Simulation Topographical Surfaces Geographical and Geological Using Differential Geometry Mohammedi Ferhat, Bensaada Said Laboratory L.A.R.H.Y.S.S, University Med Khider B.P, Biskra, Algerie E-mail: farwane@yahoo.fr Received June 9, 2011; revised August 21, 2011; accepted October 23, 2011 Abstract By applying differential geometry to analogue models developed such a model is calculated for the geomet- rical shape. Dip measurements are critical data for geologists, and in particular for structural studies. They enable quantifying geologic features observed across the surface in order to model the sub-surface. Dip measurements are provided by direct or indirect sources: geological maps, fieldwork data, Digital Elevation Model (DEM). This quantification then allows for comparison of such models to measured field data and supplants the use interferometry Radar describes and compares 3-D deformations. This example supplements and is based on the material found in L.S.S.I.T. Theory as well as some of the experimental results with the new method are delineated. Keywords: Structural Geology, Topography Surfaces, Differential Geometry, Modeling Images Optically 1. Introduction We present a mathematical analysis of interference phe- nomena for shape recognition. The basic theoretical concept —and tool—will be the contour interferences fringes function. We show that the mathematical analysis is greatly simplified by the systematic recourse to this tool. By deforming analogue theoretical models made of starting from the models carried out at the laboratory (e.g., labo- ratory-test), it is possible to create intricate 3D surfaces for comparison with optically fold surfaces. If the model surface resembles the topographical surface, inferences on the sequence and directions of Loading can be drawn for the deformation of the assembly experimental surface from the known boundary conditions of the optical images of the assembly model. However, establishing geometric similarity of the model and optically surfaces requires both surfaces to be mapped in three dimensions. Surfaces quanti- fied using differential geometry can be compared precisely for various geometric similarities and differences as a pre- requisite for kinematic and dynamic comparisons. (Figure 1) The purpose of this paper is to report an alternative method for analyzing the derivative of the surface deformation is then retrieved from a series of frames of the sheared images collected as the topographical surface is deformed, the sur- face slope is extracted. Some limitations of this method along with possible solutions are also presented. Figure 1. Topographical surfaces with curves opposed lo- cally 3D. 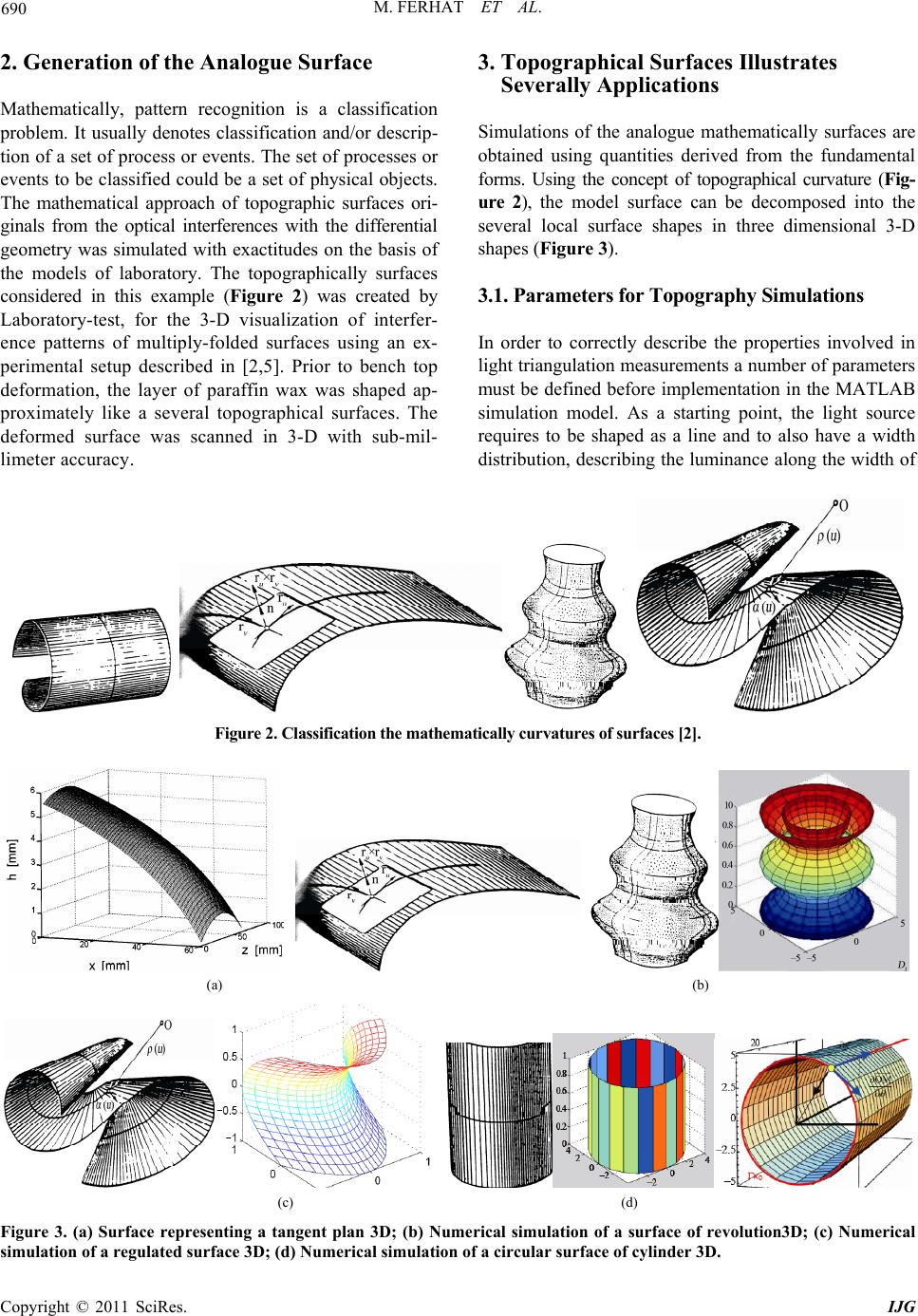 M. FERHAT ET AL. Copyright © 2011 SciRes. IJG 690 2. Generation of the Analogue Surface Mathematically, pattern recognition is a classification problem. It usually denotes classification and/or descrip- tion of a set of process or events. The set of processes or events to be classified could be a set of physical objects. The mathematical approach of topographic surfaces ori- ginals from the optical interferences with the differential geometry was simulated with exactitudes on the basis of the models of laboratory. The topographically surfaces considered in this example (Figure 2) was created by Laboratory-test, for the 3-D visualization of interfer- ence patterns of multiply-folded surfaces using an ex- perimental setup described in [2,5]. Prior to bench top deformation, the layer of paraffin wax was shaped ap- proximately like a several topographical surfaces. The deformed surface was scanned in 3-D with sub-mil- limeter accuracy. 3. Topographical Surfaces Illustrates Severally Applications Simulations of the analogue mathematically surfaces are obtained using quantities derived from the fundamental forms. Using the concept of topographical curvature (Fig- ure 2), the model surface can be decomposed into the several local surface shapes in three dimensional 3-D shapes (Figure 3). 3.1. Parameters for Topography Simulations In order to correctly describe the properties involved in light triangulation measurements a number of parameters must be defined before implementation in the MATLAB simulation model. As a starting point, the light source requires to be shaped as a line and to also have a width distribution, describing the luminance along the width of Figure 2. Classification the mathematically cu rvatures of surfaces [2]. (a) (b) (c) (d) Figure 3. (a) Surface representing a tangent plan 3D; (b) Numerical simulation of a surface of revolution3D; (c) Numerical simulation of a regulated surface 3D; (d) Numerical simulation of a circular surface of cylinder 3D.  M. FERHAT ET AL. Copyright © 2011 SciRes. IJG 691 the line. The width distribution should be easy to alter, in order to enable simulations using different light sources. The surface hit by the emitted light should be fed to the simulation model as a matrix of height values, enabling any surface, which is not merely restricted to object- surface to be simulated. Reflectance is also a parameter that requires to be input into the model. In the majority of cases, the reflectance of a surface can be said to be constant over a topographic-surface, so this parameter can be set using a constant value rather than a distributed function. Background light must also be considered, which will manifest itself as a noise level added to the reflected image seen by the camera. Since the line of light is projected onto the surface at a particular angle and is picked up by a camera at a different angle, these angles are also vital parameters for simulation. In order to de- termine the actual height of the surface at a given point, the centre of gravity of the reflected line of light must be calculated. The center of gravity of the line represents the average dislocation due to the surface topography and is used to calculate the surface height at each position of the surface matrix. The height values produced will be dependant on all of the parameters listed above. 3.2. Computer Simulation and Numerical Results of Surfaces-Geometrical Constraints We give some examples of surfaces and we can establish the mathematical relations, to position our topographic surfaces in the field of fringes with the appearance of the fringe of order zero, or central fringe. The simulation is then controlled from a standard MATLAB function Win- dow, in which the simulation model core file is included as a path. The following program example provides a brief outline regarding how the model can be used and controlled (see Figure 4(a) and (b)). 3.3. Experimental Procedure and Results By analogy between topographic surfaces, and the sur- faces plunged or immersed in 3-D map of the differential geometry one notes: - Surfaces with null curves - Surfaces with average curves - Surfaces of Weingarten - Surfaces like envelopes of plan. 3.4. Physical Analysis The physical concept is based on the functions of trans- missions of the gratings by interferences and the mathe- (a) (b) Figure 4. (a) Controller program example; (b) Matlab in- terfaces with camera scientific using image Acquisition Toolbox. matical aspect associated the objects and real topog- raphic surfaces and of the examples to the models of the laboratory. The general expression of interference effect of the function of transmission is given by: () exp2π exp 2π h h s s faih gcsi (1) From this relation comes fundamental equation of in- terferences gratings we can expressed by: 0()JJ (2) As a result, an expression for the intensity can be ex- pected to follow a sinusoidal waveform whose phase is a function of x, y, i.e.,  M. FERHAT ET AL. Copyright © 2011 SciRes. IJG 692 0sin , I Ixy (3) When gratings are overlapped on surfaces objects, the resultant interferences effect reveals the functional form of the variation. The intensity of the image can thus be expressed: (, )exp m nhs hs mn I xyaaccU (4) Especially in our method of analysis, the relative tem- poral displacement of the two objects points are compared. At the plane of the sensor, the intensity at a point on the image can be expressed: 00 (, ,)(, )1cos((, ) (,,)(,) IxytI xyxy UxytUxxyy (5) ,,Uxyt is the displacement at an object point (x,y), , Ux xy y, and U is the z-component of the dis- placement. The relative displacements and the slope along the x-y axis at the point (x,y) is d,,d d,,d Uxytx Uxyty (6) The phase is then unwrapped as in phase shifting in- terferometry and thereby a 3-D map of the time depend- ent phase be generated. The final phase can be expressed by this equation: ,,, 0 , x yxyUxyxx Uxy yy (7) where 0, x y is the initial phase which usually a constant. From these extrapolations the 3-D plot of the object slope or curvature surfaces can be extracted 0 4π, ,, Uxyx x xy xy (8) , xy xy UU UU x yxy (9) The functions x and y of normal stress and For small strains. In general solved in thought using a numeri- cal or analogical modelling according the Hook’s law. For each set of loading conditions and initial random perturba- tions, the surface is deformed starting at time zero (unre- formed aside from the initial perturbations) in time steps At which sum to the total time of deformation, tfinal. In order to compare models starting from the same pseudo- random surface but subjected to different loading condi- tions, the amount of strain induced was used as the met- ric. For small values of t Equations (6)-(7) and Equations (8)-(9) are approximately equal. This allows for direct comparison of pure shear and simple shear models at the same time steps at, as long as the total time tfinal is rela- tively small, due to the fact that the amount of maximum shortening is approximately equivalent for the pure shear and simple shear cases at each time step. 3.5. Mathematical Analysis One will limit oneself to surfaces of the Euclidean space brought back to the coordinates Cartesian X, Y, Z. One can interpreter the formula of transformation of the coor- dinated geographical (λ, φ, h) by the following formula 2 cos cos sin cos 1sin XNh Y ZNe h Nh (10) One can reverse the system (λ, φ, h) to express in function (X, Y, Z) by equation: 022 22 0 arct an cos Z X Y XY hN (11) It is an iterative and convergent process, and offers an identical numerical result. 3.6. Geometric Analysis by Segmentation with the Analogue Geographical Surface Image segmentation is a process that partitions an image into its constituent regions or objects. Effective segmen- tation of complex images is one of the most difficult tasks in image processing. Various image segmentation algo- rithms have been proposed to achieve efficient and ac- curate results. Among these algorithms, watershed seg- mentation is a particularly attractive method. The major idea of watershed segmentation is based on the concept of topographic representation of image intensity. If one compares with topography these images with a moun- tainous relief, there are parts more luminous than others (see Figure 5(a)). As pointed already, the basic concept of watershed is based on visualizing a gray level image into its topographic representation, which includes three basic notions: minima, catchment basins and watershed lines. Figure 5(b) illustrates the meanings of these defi- nitions. In the image of Figure 5(a), if we imagine the bright areas have “high” altitudes and dark areas have “low” altitudes, then it might look like the topographic surface illustrated by Figure 5(b). In this surface, it is natural to consider three types of points: 1) points be- longing to the different minima; 2) points with certainty to a single minimum; and 3) points at equally likely to fall to more than one minimum. The first type of points forms different minima of the topographic surface. The second 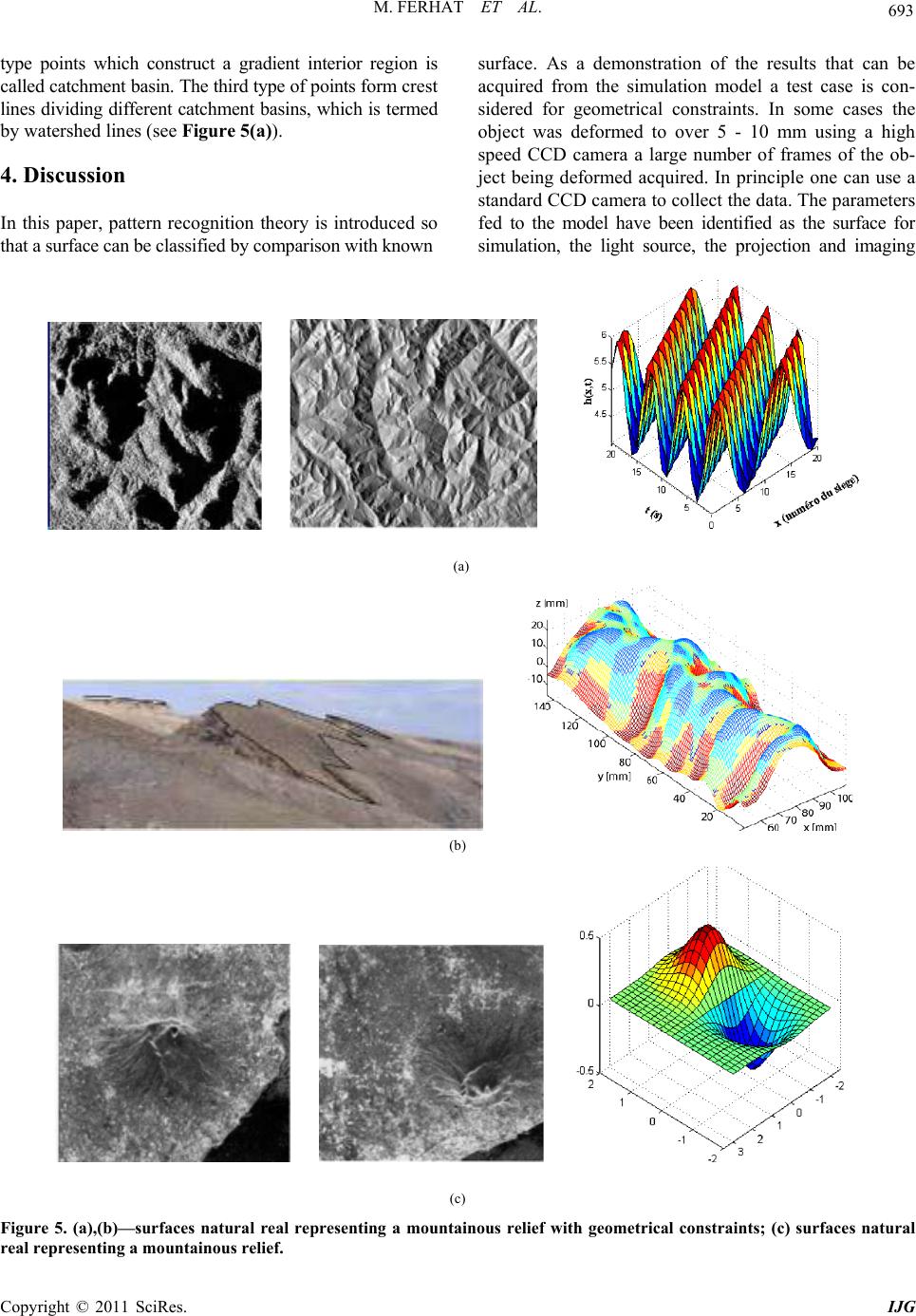 M. FERHAT ET AL. Copyright © 2011 SciRes. IJG 693 type points which construct a gradient interior region is called catchment basin. The third type of points form crest lines dividing different catchment basins, which is termed by watershed lines (see Figure 5(a)). 4. Discussion In this paper, pattern recognition theory is introduced so that a surface can be classified by comparison with known surface. As a demonstration of the results that can be acquired from the simulation model a test case is con- sidered for geometrical constraints. In some cases the object was deformed to over 5 - 10 mm using a high speed CCD camera a large number of frames of the ob- ject being deformed acquired. In principle one can use a standard CCD camera to collect the data. The parameters fed to the model have been identified as the surface for simulation, the light source, the projection and imaging (a) (b) (c) Figure 5. (a),(b)—surfaces natural real representing a mountainous relief with geometrical constraints; (c) surfaces natural real representing a mountainous relief.  M. FERHAT ET AL. Copyright © 2011 SciRes. IJG 694 angles, noise parameters and reflectance coefficients. Geologists should record and use the geographic coordi- nates (see Figures 5(b) and (c)) for every sampled point on the structures they are mapping. Meaningful interpre- tations of geological surfaces can then be presented quantitatively in light of the sampling, data precision, and motivation of the analysis. 5. Acknowledgements The authors gratefully acknowledge the financial support by the M.E.S.R.S Ministry for the Higher education and the Required Scientist of Algeria Under fundamental re- search CNEPRU-MESRS. Code du Project: D 01420090011. 6. References [1] P. Léna, “Méthodes Physiques de l’Observation,” Inter Editions/ Edition du CNRS, 1986. [2] M. Berger and B. Gostiaux, “Géométrie Différentielle, Courbes et Surfaces,” Ed. PUF, Paris, 1987. [3] F. Mohammedi, “Thèse de Doctorat, Etudes topographi- ques des Surfaces,” Louis Pasteur University, Strasbourg, 1993. [4] K. Patorski and M. Kujawinska, “Handbook of the Moiré Fringe Technique,” Elsevier Science Publishers, New York, 1993. [5] Y. Menard, “Topographie de la mer à Partir des Données Altimétriques Sea-Sat,” L’océanologie spatiale, CNES, 1982, pp. 701-721. [6] M. Robin, “la Télédétection, Nathan Université,” Série Géographie, 1995. [7] B. Han, “Recent Advancements of Moiré and Micro- scopic Moiré Interferometry for Thermal Deformation Analyses of Microelectronics Devices,” Experimental Mechanics, Vol. 38, No. 4, 1998, pp. 278-328. [8] S. De Nicola and P. Ferraro, “Fourier Transform Method of Fringe Analysis for Moiré Interferometry,” Journal of Optics A: Pure and Applied Optics, Vol. 2, No. 3, 2000, pp. 228-233. [9] L. D’Acquisto, L. Fratini, A. M. Siddiolo, “A Modified Moiré Technique for Three-dimensional Surface Topog- raphy,” Measurement Science and Technology, Vol. 13, No. 4, 2002, pp. 613-622. doi:10.1088/0957-0233/13/4/326 [10] L. Salvi, J. PagÈs and L. Batlle, “Pattern Codification Strategies in Structured Light Systems,” Pattern Recog- nition, Vol. 37, No. 4, 2004, pp. 827-849. doi:10.1016/j.patcog.2003.10.002 [11] A. Antal and D. Paveleva, “Projection Method of Re- solving Ambiguities by Determining the Order of Colors in Moiré fringes,” Applied Optics, Vol. 44, No. 36, 2005, pp. 7709-7713. doi:10.1364/AO.44.007709 [12] J. Pares and. Toscer, “les systèmes de télé- communica- tions par satellites,” Masson & Cie, ENSTA, 1975: [13] F. Mohammedi, “Modelling by a Method for Automating Moiré Images for Application in 2D-3D,” I.Re.Phy, Vol. 3, No. 2, 2009, pp. 129-134. |

