Blending Sensor Scheduling Strategy with Particle Filter to Track a Smart Target

doi:10.4236/wsn.2009.14037

Paper Menu >>

Journal Menu >>

Wireless Sensor Network, 2009, 1, 300-305

doi:10.4236/wsn.2009.14037 Published Online December 2009 (http://www.scirp.org/journal/wsn).

Blending Sensor Scheduling Strategy with Particle

Filter to Track a Smart Target

Bin LIU1, Chunlin JI1, Yangyang ZHANG2, Chengpeng HAO3

1Departme n t of Statistical Sci e n ce , Duke University, Durham , U. S. A

2Adastral Park Research Campus, University College London, London, UK

3Institute of Acoustics, Chinese Academy of Sciences, Beijing, China

Email: {bin.liu2, chunlin.ji}@duke.edu, y.zhang@adastral.ucl.ac.uk, haochengp@sohu.com

Received April 17, 2009; revised July 20, 2009; accepted July 21, 2009

Abstract

We discuss blending sensor scheduling strategies with particle filtering (PF) methods to deal with the prob-

lem of tracking a ‘smart’ target, that is, a target being able to be aware it is being tracked and act in a manner

that makes the future track more difficult. We concern here how to accurately track the target with a care on

concealing the observer to a possible extent. We propose a PF method, which is tailored to mix a sensor

scheduling technique, called covariance control, within its framework. A Rao-blackwellised unscented Kal-

man filter (UKF) is used to produce proposal distributions for the PF method, making it more robust and

computationally efficient. We show that the proposed method can balance the tracking filter performance

with the observer’s concealment.

Keywords: Particle Filter, Sensor Scheduling, Smart Target, Tracking

1. Introduction

The problem of target tracking has received considerable

attention from both academic and engineering communi-

ties. Generally, people formulate this problem as a state

estimation or filtering problem, focusing on the tracking

filter’s performance. A limitation of such works in the

literature is that it assumes that any changes in the be-

havior of the target are unconnected to the action of the

target tracking process. However, in many real-world

situations, this is an unrealistic assumption. Taking a

sonar application as an example, where the observer is an

autonomous underwater vehicle (AUV), the target, e.g., a

submarine equipped with elaborate detection instruments,

is able to detect, and, once it is aware it is b eing tracked,

it can modify its behavior quickly to escape from this

track and make the future track more difficult.

A complete solution to the problem of tracking a smart

target is still an open problem. However, some initial

results are available. Kreucher et al perform a reinforce-

ment learning approach to schedule a multi-modality

sensor to detect and track smart targets [1]. For their ap-

proach, a multi-step ahead scheduling policy is essential

to provide sensible performance. Savage et al. consider

an idealized problem where the target has a set of possi-

ble motion models and selects the one to best reduce the

sensor’s tracking performance, and treat this problem in

the framework of game theory [2]. Gittins and Roberts

use game theory to investigate the case in which a target

is trying to escape d etection [3,4]. We consid er the prob-

lem of tracking a smart target with a care on concealing

the observer to an extent and propose a smart tracker by

mixing a sensor scheduling technique with particle fil-

tering (PF) methods [5].

This paper is an expanded version of [5]. Here we

assume there are two sensors to be used by the observer,

with passive and active modalities, respectively. The

passive sensor measures the energy that has already ex-

isted in the environment, without emitting any energy

outside. Such a quite mode makes the observer conceal

itself well, but cannot guarantee the tracking perform-

ance, especially when the SNR is small. Differing from

the passive sensor, the active one emits energy to the

environment and before collecting reflected energy to do

detection. Such an active mode has substantially better

detection and tracking capabilities than the passive one,

This material is based upon work supported by the National Science

Foundation of the USA under Grant No. 0507481. C. Hao’s work was

supported by the National Natural Science Foundation of China unde

Grant No. 60802072.

B. LIU ET AL. 301

however, it makes the observer easily detected by the

target. So, employing these two sensors, there is a

contradiction between the tracking filter’s performance

and the concealment of the observer. The goal of this

paper is actually to design a method, which can both

guarantee the tracking filter’s performance and conceal

the observer to a reasonable extent. We resort to sensor

scheduling strategies and particle filtering (PF) methods

to seek a balance between these two aspects.

Sensor job (time) scheduling is within the context of

multi-sensor management. It has become increasingly

important in the research and development of modern

multi-sensor systems. Sensor scheduling lies in the first

level of a top-down policy of sensor management with

the role of assigning each sensor with a detailed

schedule on what to do [6]. PF is a Sequential Monte

Carlo method which founds great research and applica-

tions in the last decade (see [7–9] and references

therein). It beats Kalman filter, a classical method used

in the target tracking discipline, in dealing with

nonlinear dynamical and measurement models and

non-Gaussian noises in the model. Theoretically, em-

ploying enough particles, PF can provide an approxi-

mate optimal Bayesian solution to any state-space

based estimation problem. In this paper we mix a spe-

cific sensor scheduling technique, namely covariance

control [1 0], with PF methods to deal with the prob lem

of tracking a smart target. We use a Rao-blackwellised

unscented Kalman filter (UKF) [11] to produce pro-

posal distributions for the PF, making it more robust

and computationally efficient. It is shown that the

proposed method provides a balance between the

tracking filter’s performance and the observer’s con-

cealment, hence it satisfies our needs for the problem

under consideration.

The remaining of this paper is organized as follows.

Section 2 describes the dynamic models involved. Sec-

tion 3 presents the sensor scheduling technique, covari-

ance control. The proposed PF algorithm is illustrated in

Section 4 and its performance is evaluated in Section 5.

Finally we conclude this paper in Section 6.

2. Models

In this section, we describe the models involved in this

paper. First the dynamic model for the target is presented.

Then the measurement models are derived for both the

passive and the active sensors.

The evolution of the target state, , is modeled by a

discrete time linear Gaussian: xk

1



xFx

(1)

where





0,Q

vN . Here the target state vector is com-

posed of the position and velocity items in the

and

coordinates and is defined as follows:















x

ktk tk

xxyy (2)

where the dot denotes the operation of first order deriva-

tive and the superscript T denotes transposition of a

matrix. We use a constant-velocity process model for the

target, so that















FF, (3)







F



and















QQ, (4)

T/3 T/2

T/2 T







where T is the sampling period,

qis the power spectral

density of the acceleration noise in the spatial dimen-

sions.

Defining









kokok

as the observer’s position

at time step , we derive measurement functions for

both the passive and the active sensors in the following.

We consider the case where the passive sensor only pro-

vides relative bearings measurements originated from the

target, then the associated measurement function is

atan













ztk ok

tk ok

xx n

yy (5)

where .

(0, )R

We assume the observer adopts a track-while-scan

sensor [10] to do active sensing, which can measure both

the bearings and the ranges. The associated measurement

function is denoted as

kz



,, ,,

atan ,() (),







 

 





tk ok

tk oktkok

yy xx yynr (6)

where denotes the noise item in the range.

So the covariance matrix of the measurement noise is

. Here denotes the operation of dia-

gonalization.

(0, )R

rN d[, ]RR

diag diag

302 B. LIU ET AL.

3. A Sensor Scheduling Technique:

Covariance Control

In this section we present the sensor scheduling tech-

nique, called covariance control, which will be embed-

ded in the PF framework described in Section 4.

Covariance control begins with a desired covariance

matrix, which is this approach differs from many other

sensor management algorithms. A desired covariance

matrix for an -dimensional state estimate,

, is de-

fined by all elements of that matrix. The goal is to

find a specific sensor combination that produces co-

variance matrix P, assuring the difference

nni



i is

positive semi-definite. To properly evaluate that differ-

ence, a scalar metric is needed. A variety of these exist,

including functions based on the determinant or the trace

of the matrix. However, these metrics rely on the positive

definiteness of the matrix to provide accu rate evaluations.

If a difference is only semi-definite, then the determinant

is zero, possibly masking a large difference in a different

direction (note that a covariance can be represented as an

ellipsoid, whose axes directions can be indicated by the

eigenvectors of the covariance matrix). A similar prob-

lem exists with the trace, where a large positive differ-

ence can mask a large negative difference along a dif-

ferent direction. To avoid these problems, M. Kalandros

and L. Y. Pao, examined other techniques, such as the

eigenvalue/minimum sensors algorithm, the matrix norm

algorithm and the norm/sensors algorithm [10]. The

norm/sensors algorithm relaxes the requirements of the

matrix norm technique, allowing the norm of the covari-

ance difference to vary within a predefined boundary



. So we borrow the idea of the norm/sensors algo-

rithm and propose the following sensor scheduling strat-

egy:

·If



PP

k (7)

select the active sensor to work for next time step;

·Else

select the passive sensor to work for next time step.

P denotes the covariance matrix associated with the

estimate for the target state at the k th time step)

Note that the aim of this sensor scheduling strategy is to

select an appropriate sensor for use for next iteration of the

tracking process, other than to search a sensor combination

that can work with the fewest sensors involved, which is

the purpose of the methods proposed in [10].

4. Particle Filtering Algorithm

This section presents our proposed PF algorithm. First

we give a brief introduction for a basic PF method. Then

we describe the Rao-blackwellised UKF [11], which is

used to produce p roposal distribution s for our PF method.

Finally we mix the sensor scheduling technique pre-

sented in Section 3 with the PF algorithm, leading to the

proposed method for tracking a smart target.

Particle filter is a Sequential Monte Carlo method,

whose basic idea is very simple: the target distributio n is

represented by a weighted set of Monte Carlo samples.

These samples are propagated and updated using a se-

quential version of importance sampling as new meas-

urements become available. We summarize a basic PF

algorithm as follows, while referring the reader to [7–9]

for detail discussions on PF methods.

Algorithm 1: Basic Particle Filter Algorithm

 Initialization. Sample

equally weighted parti-

cles from the initial pdf of the target state,





xp:

 For 1, ,



iN



000

;



xx

 Set 0



 Iteration 1



 Sampling new particles from proposal distribution







, i.e.,

For 1,,



iN





1



x

 Evaluate importance weights:





 



11 1



 



zx xx

kk kk

 Normalize the importance weights su ch that







i

k, and









 Selection step: Multiply/Suppress particles with

high/low importance weights respectiv ely, resulting in a

set of equally weighted particles, .

1,1,,

x

kiN

 Output:









 



1111





 



xxxxx

CovE E

1

The design of the propo sal d istrib ution , i.e.,







q, is of

paramount importance for the PF algorithm. It has been

shown that UKF can be used to produce good proposal

distributions, particularly when the observation model is

nonlinear [12]. The idea is that one treats a Guassian

distribution outputted by the UKF as the PF’s proposal

distribution. It is shown that Rao-blackwellization tech-

nique can be used to improve the UKF’s computational

efficiency [11]. So here we adopt the Rao-blackwellised

B. LIU ET AL. 303

UKF (RB-UKF) to generate the PF’s proposal. An im-

plementation of RB-UKF based on the models described

in Section 2 is summarized as follows.

Algorithm 2: RB-UKF Algorithm

Assume we have got the estimate for the target state at

time step k, , with its corresponding covariance, ,

the goal is to solve and , as a new measure-

ment arrives.

xkPk

1

xk1

1

 Linear State Prediction:





Fx



PQFPF

 Sigma points sampling





, 1



 







, ,

 



 

ipp i

for

1, ,in





, ,

 



 

ipp i

for

1,, 2in n

where is the dimension of the state vector, and





, and



are parameters prescribed beforehand for the

UKF.

 Nonlinear measurement update based on Unscented

Transform

 n

. (





,, 0,1,,2



z

iu i



h denotes the meas-

urement function)









nc

uiiu

 z











Pzzz



cuu

ui iuiu



 





ciipiu

11



 z



0i

1

KPP





z



xK



1PPKPK

kpu

Next we use such RB-UKF algorithm to generate

proposal distributions for the PF, and mix the sensor

scheduling technique proposed in Section 3 into the PF

framework, leading to the proposed PF algorithm.

Algorithm 3: The Proposed PF Algorithm for Smart

Target Tracking

 Initialization.

 Sample N equally weighted particles from the

initial pdf of the target state,





 Assign specific values for the desired covariance

matrix, Pd, and



 Set 0



 Sensor scheduling for the next time step: use the

active sensor while keep the passive one idle



k  Iteration

 For 1, ,



iN

 Perform RB -UKF algorithm toxi

k to get











 Sample a new particle from the proposal distribu-

tion:





P



11

xx

 Evaluate importance weights:





 



11 1



 



x

kk kk

||zx xx

iii

Normalize the importance weights such that







k

ki

,1xiiN

, and







i

 Selection step: Multiply/Suppress particles with

high/low importance weights respectiv ely, resulting in a

set of equally weighted particles, ,,.

1k

 Output:











11111



 



xxxxx

kkkkk

CovE E

1i

 Sensor scheduling for the next time step:

 If











Pxk

Cov

select the active sensor to work while keep the passive

one idle;

 Else, select the passive sensor to work while keep

the active one idle.

5. Performance Evaluation

In this section, we evaluate the performance of our pro-

posed method in Section 4 by simulations. First, we

compare the tracking performance of our method with

those of two other trackers, one adopting the passive

sensor for detection and the other utilizing the active

sensor for detection, based on a set of Monte-Carlo (MC)

simulations. The purpose of this comparison is to dem-

onstrate the effect of the sensor scheduling technique in

the aspect of concealing the observer. Next, we investi-

gate the effects of the parameter



on our method’s

performance. This parameter is used to measure the dif-

ference between the desired covariance and the current

estimation covariance in the sensor scheduling stage of

our method.

304 B. LIU ET AL.

The scenario to be investigated is shown in Figure 1.

The observer travels at a fixed speed of 10m/s and exe-

cutes 2 maneuvers. The observation period lasts 40 sec-

onds. The target motion, described by (1) in this simula-

tion, is subjected to an amount of process noise with

. The initial position and speed of the target are

and

1

300 ,



300mm





12.25, 12.25msms , respectively. The

other parameters for simulation initialization are summa-

rized in Table 1.

For performance comparison, we take the root-mean

square (RMS) position error as the index:



,,,

RMS



 



Mii

ktk tk

Mxy

)

(8)

where ,,

tktk

y and ,

tk )

x denote the true and the

estimated target positions at time step k at the ith MC run,

and M is the total number of independent MC runs. Here

runs are done for the following three trackers,

the proposed sensor scheduling based PF (SS-PF) tracker,

the passive/active mode PF (PaPF/AcPF) tracker which

only use the passive/active sensor in the filtering pro cess.

As shown in Figure 2, the performance of the proposed

SS-PF tracker is comparable to that of the AcPF tracker,

and it is much better than that of the PaPF tracker. For

the SS-PF tracker, the average number of time epochs,

when the active sensor is used during the whole tracking

process, is only 13. It means that the SS-PF tracker gets a

similar filtering performance as that of the tracker which

uses the active sensor all the time, while concealing the

observer to an extent by reducing the use of the active

sensor. A specific estimation result of this SS-PF for the

target’s trajectory is shown in Figure 1; the associated

sensor scheduling result is also illu strated in Figure 4. As

can be seen, at first, the SS-PF tracker selects the active

sensor to do detection to get a good enough tracking ini-

tialization, then it dynamically switch the uses of the

passive and the active sensors online. The sensor switch

50M

uses of the passive and the active sensors online. The sen-

Table 1. Parameters used for initialization.

Symbol Quantity Value

T Sampl ing period 1s

σb Standard error of bearing noise 1˚

σd Standard error of range noise 5m

N Particle Number 200

desired covariance matrix diag([5 0.25 0.2])

predefined boundary for

the norm of covariance

Figure 1. The observer’s and the target’s movement trajec-

tories in this experiment.

Figure 2. RMS position error versus time. PaPF and AcPF

denotes passive mode and active mode PF tracker respectively,

and SS-PF denotes the proposed tracker in this paper.

Figure 3. The true target trajectory against the estimated

one by the proposed PF tracker.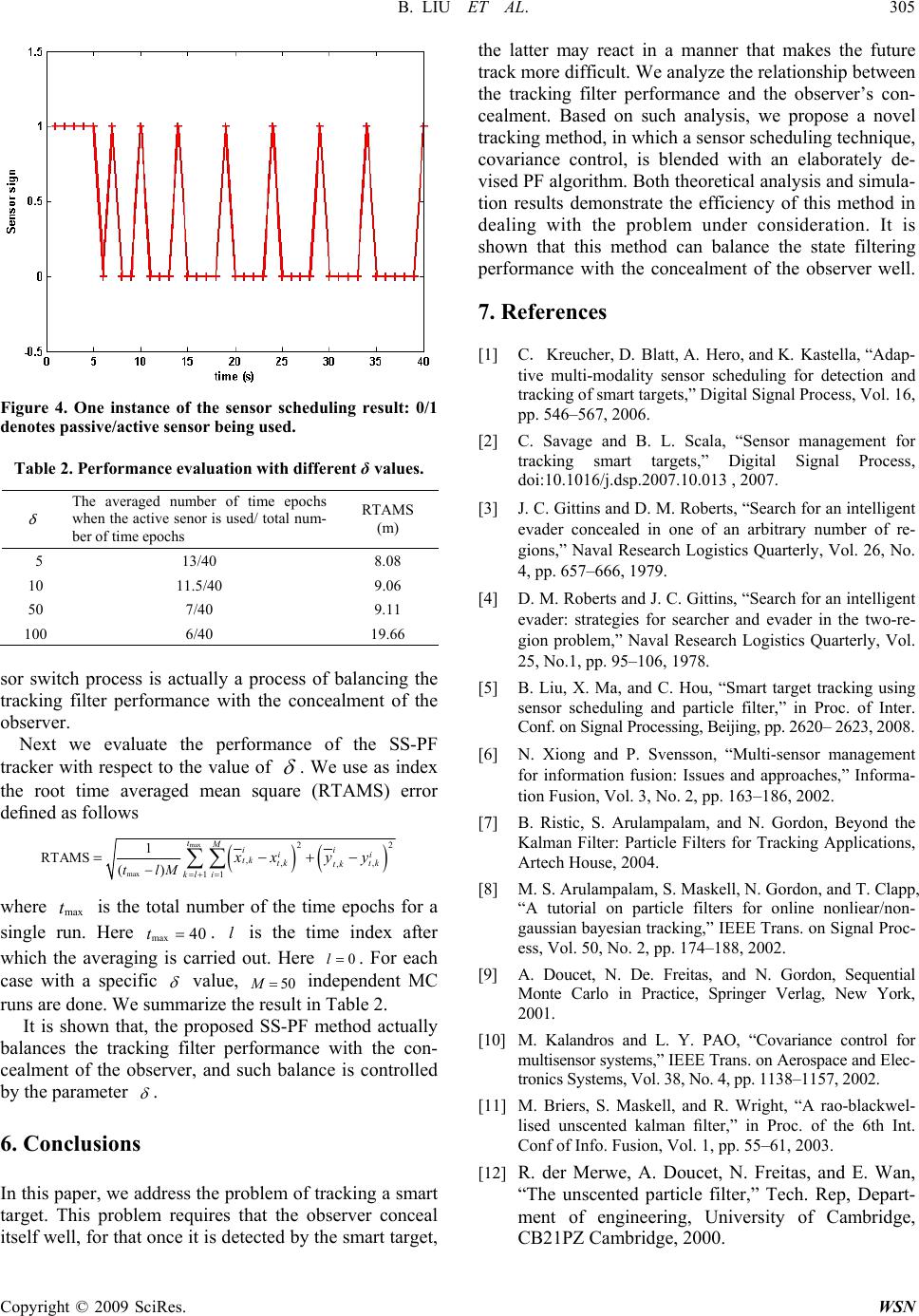

B. LIU ET AL. 305

the latter may react in a manner that makes the future

track more difficult. We analyze the relationship between

the tracking filter performance and the observer’s con-

cealment. Based on such analysis, we propose a novel

tracking method, in which a sensor scheduling technique,

covariance control, is blended with an elaborately de-

vised PF algorithm. Both theoretical analysis and simula-

tion results demonstrate the efficiency of this method in

dealing with the problem under consideration. It is

shown that this method can balance the state filtering

performance with the concealment of the observer well.

7. References

[1] C. Kreucher, D. Blatt, A. Hero, and K. Kastella, “Adap-

tive multi-modality sensor scheduling for detection and

tracking of smart targets,” Digital Signal Process, Vol. 16,

pp. 546–567, 2006.

Figure 4. One instance of the sensor scheduling result: 0/1

denotes passive/active sensor being use d.

Table 2. Performance evaluation with different δ values.

The averaged number of time epochs

when the active senor is used/ total nu m-

ber of time epochs

RTAMS

(m)

5 13/40 8.08

10 11.5/40 9.06

50 7/40 9.11

100 6/40 19.66

[2] C. Savage and B. L. Scala, “Sensor management for

tracking smart targets,” Digital Signal Process,

doi:10.1016/j.dsp.2 007.10.013 , 2007.

[3] J. C. Gittins and D. M. Roberts, “Search for an intelligent

evader concealed in one of an arbitrary number of re-

gions,” Naval Research Logistics Quarterly, Vol. 26, No.

4, pp. 657–666, 1979.

[4] D. M. Roberts and J. C. Gittins, “Search for an intelligent

evader: strategies for searcher and evader in the two-re-

gion problem,” Naval Research Logistics Quarterly, Vol.

25, No.1, pp. 95–106, 1978.

sor switch process is actually a process of balancing the

tracking filter performance with the concealment of the

observer.

[5] B. Liu, X. Ma, and C. Hou, “Smart target tracking using

sensor scheduling and particle filter,” in Proc. of Inter.

Conf. on Signal Processing, Beijing, pp. 2620– 2623, 2008.

Next we evaluate the performance of the SS-PF

tracker with respect to the value of



. We use as index

the root time averaged mean square (RTAMS) error

deﬁned as follows

[6] N. Xiong and P. Svensson, “Multi-sensor management

for information fusion: Issues and approaches,” Informa-

tion Fusion, Vol. 3, No. 2, pp. 163–186, 2002.



max

,,,

RTAMS ()

 







tMii

tk tk tk

kl i

tlM xx yy

[7] B. Ristic, S. Arulampalam, and N. Gordon, Beyond the

Kalman Filter: Particle Filters for Tracking Applications,

Artech House, 2004.

[8] M. S. Arulampalam, S. Maskell, N. Gordon, and T. Clapp,

“A tutorial on particle filters for online nonliear/non-

gaussian bayesian tracking,” IEEE Trans. on Signal Proc-

ess, Vol. 50, No. 2, pp. 174–188, 2002.

where is the total number of the time epochs for a

single run. Here . is the time index after

which the averaging is carried out. Here . For each

case with a specific

max

max 40tl

0l



value, independent MC

runs are done. We summarize the result in Table 2.

50M[9] A. Doucet, N. De. Freitas, and N. Gordon, Sequential

Monte Carlo in Practice, Springer Verlag, New York,

2001.

It is shown that, the proposed SS-PF method actually

balances the tracking filter performance with the con-

cealment of the observer, and such balance is controlled

by the parameter



[10] M. Kalandros and L. Y. PAO, “Covariance control for

multisensor systems,” IEEE Trans. on Aerospace and Elec-

tronics Systems, Vol. 38, No. 4, pp. 1138–1157, 2002.

[11] M. Briers, S. Maskell, and R. Wright, “A rao-blackwel-

lised unscented kalman ﬁlter,” in Proc. of the 6th Int.

Conf of Info. Fusion, Vol. 1, pp. 55–61, 2003.

6. Conclusions

[12] R. der Merwe, A. Doucet, N. Freitas, and E. Wan,

“The unscented particle filter,” Tech. Rep, Depart-

ment of engineering, University of Cambridge,

CB21PZ Cambridge, 2000.

In this paper, we address the problem of tracking a smart

target. This problem requires that the observer conceal

itself well, for that once it is detected by the smart target,