Open Access Library Journal
Vol.05 No.05(2018), Article ID:84729,9 pages
10.4236/oalib.1104625
Simulation Research on PID Control of Automotive Stability Based on Genetic Algorithm Optimization
Rongxu Zhang, Bo Zhao
Shanghai University of Engineering Science, Shanghai, China

Copyright © 2018 by authors and Open Access Library Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 26, 2018; Accepted: May 20, 2018; Published: May 23, 2018
ABSTRACT
According to the ideal vehicle model with two degrees of freedom of the transverse effect of yaw rate and sideslip angle of the vehicle stability, the yaw rate and side slip angle as the control parameter of vehicle stability control system, through the PID control algorithm and the Genetic Optimization PID control algorithm is studied on the simulation diagram, and building in matlab/simulink, the author makes a comparison and simulation analysis results of the two algorithms. Through the combination of simulation results, Genetic Optimization PID control algorithm has better control effect than PID control algorithm. The amplitude of the yaw rate and sideslip angle and the overshoot is significantly reduced, significantly improving the stability of automobile when steering.
Subject Areas:
Mathematical Analysis, Mechanical Engineering
Keywords:
Vehicle Stability Control, Combined Simulation, Genetic Optimization PID Algorithm

1. Introduction
The stability of a car during a sharp turn has always been an important issue when it comes to high speed and safety. When the vehicle turning or changing lanes is at high speeds, the car will produce yaw motion in centrifugal force greatly; when the ground adhesion coefficient is low, the car will take place immediately and sideslip; once produced, road vehicles will face lateral effect weakened rapidly; the driver through the steering wheel control effect on the car will become very obvious; the car will quickly lose stability [1] . Based on the research status of automotive stability at home and abroad, this paper selects two control parameters for the stability of the vehicle, and optimizes the PID control through genetic algorithms.
2. Vehicle Two Degree of Freedom Model
Forward at a constant speed for the car’s lateral movement and horizontal pendulum movement can make use of two degrees of freedom linear model of a car, and it only yawing angular velocity and mass center side-slip Angle two degrees of freedom, this article selects two degrees of freedom linear model car as the research object, according to the Newtonian mechanics for two degrees of freedom vehicle movement differential equation is as follows.
In the formula, k1 and k2 are the front and rear wheel’s cornering stiffness respectively, and the unit is N/rad; IZ is the moment of inertia of the car around the z-axis, and the unit is kg・m2; β is the centroid side-bias angle and the unit is rad; The yaw rate is rad/s; vx, vy are the longitudinal and lateral speeds, respectively, in units of m/s; lf, lr are the distances from the center of mass of the vehicle to the front and rear axles, in mm; δf For the front wheel corner, the unit is; m is the whole vehicle mass, and the unit is kg.
3. Genetic Optimization PID Control Algorithm Research
3.1. PID Control Algorithm and Parameter Selection
PID control algorithm [2] is mainly composed of PID controller and controlled object. The schematic diagram is shown in Figure 1.
In Figure 1, u(t) is the control output, r(t) is the given value, y(t) is the output of the controlled object, and e(t) is the deviation between the given value and the actual output value.
Figure 1. PID control schematic.
3.2. PID Parameter Optimization Strategy Based on Genetic Algorithm
The basic operation of genetic algorithm [3] can be divided into three steps: selection, crossover, and mutation. The selection operation is also referred to as a copy operation, and it is determined based on the degree of merit of the individual’s fitness function value to determine whether it is inherited or eliminated. The crossover operation is to exchange the partial code values of the selected two individuals. The variability operation is to change the digits in a position on the digital string. The genetic algorithm operation process is shown in Figure 2.
Firstly, the three parameters of PID Kp, Ki, and Kd are combined together as each individual in the genetic algorithm group, and then the fitness value of each group of parameters is calculated according to the fitness function; secondly, the groups are selected, crossed, and mutated. The operation continues to evolve until it finds the optimal target individual in the population, thereby obtaining the optimal parameters of the PID controller. The controller based on genetic algorithm optimization is mainly composed of three parts: PID controller: it directly controls the controlled object in closed loop, and performs online dynamic optimization of three parameters Kp, Ki, Kd; genetic algorithm: it is based on the system Dynamic operating state, adjust the three parameters of the PID controller to achieve the optimization of a certain performance index; evaluation link: According to the initial input data, the data adjusted by the PID controller and the output data are compared and analyzed to see if it reaches a certain The performance index requirements are then fed back to the genetic algorithm for further optimization. Its control system block diagram is shown in Figure 3.
Figure 2. Schematic diagram of the execution of the genetic algorithm.
Figure 3. PID controller system structure diagram based on genetic optimization.
3.3. PID Controller Genetic Optimization
Genetic optimization has the following steps for PID [4] controller parameter optimization:
1) Parameter coding
Binary parameter encoding is generally used. First of all, each parameter is generated by sub-string binary coding, and then in accordance with a certain sequence of each sub-string into a large binary string, that is, our individual. Set the range of each parameter, and then determine the length of these three substrings based on the accuracy. The spatial binary parameters and the solution set space integer determine a mapping relationship.
2) Generation of the initial population
First, based on the specific problem, determine the number of populations as N. The smaller the value of N, the faster the genetic algorithm will operate, but it will reduce the diversity of individuals, which will cause the algorithm to appear early convergence. On the contrary, the greater the value of N, the greater the diversity of the population, and the corresponding genetic algorithm will reduce the speed of calculation, and the value of N is generally taken as 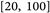 [5] . Secondly, according to the population N, we randomly generate the first generation population.
[5] . Secondly, according to the population N, we randomly generate the first generation population.
3) Fitness function
The so-called PID parameter optimization, in fact, is to use an optimization algorithm to optimize the three parameters of the PID Kp, Ki, Kd, the essence of which is based on a certain target function parameter optimization problem, and the objective function is the fitness function.
4) Setting control parameters
Setting the control parameters determines the number of iterations G, the mutation probability Pm, and the crossover probability Pc.
The number of iterations G. Iterations is actually the parameter of the genetic algorithm at the end of the run. It means that the genetic algorithm runs after reaching the specified number of iterations, and the output optimal solution is the best individual of the current population.
Variation probability Pm. Considering the influence of mutation operation in genetic algorithm, if the value of Pm is relatively large, a relatively large number of new individuals will be generated, but it is also possible to destroy more good models; if the value of Pm is small, the mutation operation will produce new ones. The individual’s ability will weaken. Crossover probability Pc. Crossover is the main method of generating new individuals by genetic algorithms, so the crossover probability generally takes a larger value. If the value of Pc is large, it will destroy the fine patterns in the population; if the value is small, the speed of producing new individuals will be slower. Usually the value of Pc is 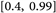 [6] .
[6] .
5) Select operation
The selection operation is based on the evaluation of the individual’s fitness. Individuals with higher fitness are more likely to inherit to the next generation, and those with less fitness are less likely to inherit. In this paper, we use the more common selection operator-proportional selection operator in genetic algorithm.
6) Crossover operation
A crossover operator refers to the exchange of some genes between two mutually matched chromosomes in a certain way, thus creating two new individuals. Crossover operation is an important feature of genetic algorithm that is different from other evolutionary algorithms. It plays a key role in genetic algorithm and is the main way to generate new individuals.
7) Mutation operation
From the aspect of the ability of genetic algorithm to generate new individuals, cross-operation is the main method to generate new individuals, which determines the global search ability of genetic algorithm; while mutation operation is an auxiliary method to generate new individuals, but it is also not an option. Missing operation steps because it determines the local search ability of the genetic algorithm. The block diagram of the genetic optimization PID is shown in Figure 4.
4. Simulation Research and Analysis
In this study, a virtual vehicle model was established in ADAMS/Car, and a joint simulation of MATLAB and ADAMS was performed. Simulate the analysis of a car under extreme conditions to verify the effectiveness of the controller, and compare the PID algorithm with the control effect of genetic optimization PID algorithm. The main parameters of the vehicle model are shown in Table 1.
The simulation conditions are as follows: vehicle speed 120 km/h, steering wheel angle 90˚, step time 1 s, and road surface adhesion coefficient 0.4. Simulation results are shown in Figure 5.
It can be seen from Figure 5(a) and Figure 5(b) that the steady-state values of the PID control algorithm and the genetic optimization PID control algorithm
Table 1. The main parameters of the vehicle model.
Figure 4. PID process diagram of genetic optimization.
[7] are basically the same, but the yaw rate and the centroid slip angle of the PID control algorithm are genetically optimized. The amount of adjustment should be less than the use of PID control algorithm and overshoot when there is no control. It can also be seen from Figure 5(b) and Figure 5(c) that the stability time of the yaw rate and the centroid slip angle based on the genetic optimization PID control algorithm is obviously less than the other two cases. In terms of lateral acceleration, Figure 5(c) shows that the genetic optimization PID control algorithm first enters the steady state range [8] , and the overshoot and the stability value are smaller.
It can be seen from the comparison that the genetic optimization PID control
Figure 5. Simulation results. (a) Yaw rate. (b) Centroid slip angle. (c) Lateral acceleration.
algorithm can effectively improve the transient dynamic response of the vehicle while maintaining the steady state response [9] . Because the algorithm uses yaw rate and the slip angle of the mass center as the state variables to control, and these two variables are the two main parameters describing the dynamic performance of the car, the simulation results obtained will be more comprehensive and accurate. And it is an ideal control algorithm.
5. Conclusion
This study discusses the causes of automotive side-slip, and briefly outlines the linear two-degree-of-freedom vehicle dynamics model. In order to overcome the shortcomings of vehicle steering instability, the designed controller is compared with no-control and PID controller. The simulation results show that the genetic algorithm to optimize the PID control is significantly better than the first two and that the optimized parameters are effective. The optimized yaw rate and lateral slip angle of the mass center are smaller, the tracking effect is good, and the lateral acceleration enters the steady-state range quickly. At the same time, the stability of the car is obviously improved.
Cite this paper
Zhang, R.X. and Zhao, B. (2018) Simulation Research on PID Control of Automotive Stability Based on Genetic Algorithm Optimization. Open Access Library Journal, 5: e4625. https://doi.org/10.4236/oalib.1104625
References
- 1. Automotive Encyclopedia Editorial Committee. (1992) Car Encyclopedia. Volume 1, Mechanical Industry Press, Beijing, 70-80.
- 2. Tao, Y.H. (1998) New Type PID Control and Its Application. Mechanical Industry Press, Beijing, 165-191.
- 3. Ding, Y.L. (2008) Research on Parameter Optimization of PID Controller Based on Genetic Algorithm. North China Electric Power University, Hebei.
- 4. Niu, J.J., Wang, Y.J. and Tang, J. (2010) Research on Parameter Optimization of PID Controller Based on Genetic Algorithm. Computer Simulation, 27, 180-182.
- 5. Feng, J.Z. (2005) Study on Electronic Throttle and Genetic PID Algorithm of Light Vehicle TCS. Master Thesis, Jilin University, Changchun.
- 6. Zhou, M. (1999) Principles and Applications of Genetic Algorithms. National Defense Industry Press, Beijing.
- 7. Zhou, H.N. and Tao, J.M. (2008) The Influence of Lateral Slip Angle and Yaw Rate on Vehicle Stability. Journal of Hubei Automotive Industry Institute, 22, 6-10.
- 8. Liu, Y. (2003) Study on the Control Algorithm of Vehicle Stability under Driving Con-ditions. Jilin University, Changchun.
- 9. Li, Z.F. (2000) Dynamic Simulation of Multi-Body System of Vehicle. Tongji Uni-versity, Shanghai.







