 Journal of Signal and Information Processing, 2011, 2, 308-315 doi:10.4236/jsip.2011.24044 Published Online November 2011 (http://www.SciRP.org/journal/jsip) Copyright © 2011 SciRes. JSIP 1 A Dyadic Wavelet Filtering Method for 2-D Image Denoising Yonggui Zhu*, Xiaolan Yang School of Science, Communication University of China, Beijing, China. Email: *ygzhu@cuc.edu.cn Received January 11th, 2011; revised July 16th, 2011; accepted July 24th, 2011. ABSTRACT We improve spatially selective noise filtration technique proposed by Xu et al. and wavelet transform scale filtering approach developed by Zheng et al. A novel dyadic wavelet transform filtering method for image denoising is proposed. This denoising approach can reduce noise to a high degree while preserving most of the edge features of images. Dif- ferent types of images are employed to test in the numerical experiments. The experimental results show that our filtering method can reduce more noise contents while maintaining more edges than hard-threshold, soft-threshold filters, Xu’s method and Zheng’s method. Keywords: Dyadic Wavelet Transform, Image Edges, Denoisin 1. Introduction Wavelet transform is a multi-resolution representation of a signal or image. It is a powerful tool in several areas of applications like signal processing, image processing, pattern recognition, data compression, commutation, etc. Singularities and irregular structures often carry essential information in signals and images. For example, the dis- continuities of the intensity of an image indicate the lo- cations of edges. The local regularity is characterized by the decay of the wavelet transform amplitude across scales. Signal singularities and image edges can be detected by the dy- adic wavelet transform modulus maxima across scales [1,2]. In mathematics, singularities are generally measu- red with Lipschitz exponents. The wavelet theory proves that these Lipschitz exponents can be calculated from the propagating amplitude values of the different modulus maxima across scales. The original signal or image has singularities whose Lipschitz exponents are greater than or equal to zero, and the noise has singularities whose Lipschitz exponents are less than zero. Thus, the amplitudes of signal or image modulus maxima increase when the scale increases, wh- ile the amplitude of noise modulus maxima decrease str- ongly when the scale increases. By using these properties, the noises can be eliminated from the noised signals or images. The approaches for separating signal and noise in wavelet scale space are proposed by many researchers. For example, the original signal can be extracted from the noisy version by estimating the signal modulus max- imum at small scales [1,2]. Adaptive Wiener filtering were used to remove noise in signals and images [3-5]. The selective noise filtration technique and adaptive thr- esholding function in image denoising were developed [6-8]. The scale space filtering algorithms applied to im- age denoising were also proposed [9,10]. In addition, many other novel approaches for image denoising have been presented by some researchers [11-13] recently. In this work, we develop an image denoising approach by improving spatially selective noise filtration technique proposed by Xu et al. [6] and wavelet transform scale filtering approach given by Zheng et al. [9]. Hard-thr- eshold and soft-threshold filters that were proposed by D. L. Donoho [14,15] are widely used in image denoising processing. We will compare our filtering approach with hard-threshold filtering, soft-threshold filtering, Xu’s me- thod and Zheng’s method in the numerical experime- nts. Peak-Signal-Noise-Rate (PSNR) and Root-Mean-Square- Error (RMSE) are employed to estimate the quality of restored images. 2. 2-D Dyadic Wavelet Transform Let 12 , k x (k = 1, 2) be wavelet functions. We denote that 112 12 2 212 12 2 1 2 1 ,, 222 1 ,, 222 j j jjj jjj xx xx xx xx (1)  A Dyadic Wavelet Filtering Method for 2-D Image Denoising309 The wavelet transform of 22 12 , xxL R at the scale 2 Is 11 12 12 22 22 12 12 22 ,, ,, jj jj Wfxx fxx Wfxx fxx (2) The set of functions 12 12 12 22 ,, , jj WfW fxxWfxx is called 2-D dyadic wavelet transform of 12 , xx . The Fourier transforms of 1 12 , x and 2 12 , x are 1 12 ˆ, and 2 ˆ 12 , 1 We suppose that12 , x , 2 12 , x are recon- structed wavelet functions. If their Fourier transforms satisfy 11 12 12 11 12 12 ˆˆ 2,2 2,2 1 ˆˆ 2,2 2,2 jj jj jj jj j (3) Then 12 , xx can be reconstructed from their dyadic wavelet transform i.e. 11 12 22 12 11 12 22 , , , jj jj j Wf xx fxx Wf xx (4) Because of the limitation of image’s resolution, we int- roduce a smoothing function 12 , x Whose Fourier transform satisfies 11 212 12 12 22 112 12 ˆˆ 2,2 *2,2 ˆ, ˆˆ 2,2 2,2 jj jj jj jj j (5) We define the smoothing operator 2 S by 12 12 22 12 12 2 ,, 1 ,, 222 jj jjjj Sfxx fxx xx xx (6) The wavelet transform between the scales 1 and 12 12 12 22 1 2,,, jj J J W fxxWfxx provides the details that are in but that have lost in . 112 ,Sfx x 12 2, j Sfxx Mallat [1] has given the fast algorithm for the discrete dyadic wavelet transform. The fast dyadic wavelet trans- form can also be calculated with a filter bank algorithm called the algorithm trous proposed by Holschneider, Kronland-Martinet, Morlet and Tchamitchian [16]. In this paper, we use trous algorithm to reconstruct the image. a a 3. Dyadic Wavelet Transform Filtering Algorithm In recent years, some denoising techniques based on the wavelet transform have been studied by many authors [2,6,12,17]. The edge modulus maxima can be distin- guished from noise modulus maxima by analyzing the singularity properties of wavelet transform domain ma- xima of a signal or image across scales [2]. Y. Xu [6] developed wavelet transform domain filters based on the direct spatial correlation of the wavelet transform at sev- eral adjacent scales. Y. Zheng [9] proposed a wavelet transform scale filtering algorithm by using the proper- ties of signal and noise modulus maxima across large scales. Our approach relies on the variations of the dy- adic wavelet transform data across all scales to remove noises rather than extracting edges directly. For a 2-D image, the discrete sampling of 12 21 , j k J Wfxx is given by 2 12 12 12 12 22,, ,, 1 d jj kk xx kk WfkkWfxxjJ (7) The discrete coarse smoothed image is denoted by 2 12 12 12 12 22,, ,, JJ d xx kk Sfkk Sfxx (8) In the scale space, the modulus maxima of 2 across scales produced by image edges have positive correlation. When the scale increases, the amplitudes of modulus maxima coeffcients will increase or retain constant. On the contrary, the modulus maxima produced by noises have negative correlation and the amplitudes of their coeffcients decrease as increases. k d j Wf j j Define 2-scale correlation as 12 12 2, ,1, 1, 2,,1,,,1,, kkk CrmnWc mnWc mn mJnnnnn , N . (9) where J re- presents the maximum scale of the decomposition. 12 22 ,, d mm kk kd Wcm nWfnWfnn The 2-scale direct correlation sharpens and enhances major edges while suppressing noise and small features. So comparing the values of and can separate important edges from noise in images. Before comparison, needs to be rescaled to Xu’s rescaling scheme is 2, k Crmn 2 k Crmn , k Wcm n , , k Wcm n 2, 2,2 kkk Crm nCrmnPWmPCrm k , (10) where 22 k k n PCrmCrm n and 2 , k k n Wm Wcmn. Copyright © 2011 SciRes. JSIP  A Dyadic Wavelet Filtering Method for 2-D Image Denoising 310 Zheng et al. use the modulus maxima rescaling method at large scales, and apply the above mentioned rescaling method at small scales. Let S be the upper limit of small scales, assume 2 12 , max2, ,1 kk nnn crmCrm nmS (11) and ,,1 kk wcmWcmm S (12) The modulus maxima rescaling formula as follows: 2, 2,,1 k kk k Mwc m Crm nCrm nmS Mcr m (13) At small scales, noise in the noised image is dominat- ing except some sharp image edges. According to Xu and Zheng’s ideas, if compare 2, k Crm n with , k Wcm n directly, then too much noise will be ext- racted as edges. To avoid this drawback, we apply the modulus maxima rescaling at all scales and renew the formula (13) as 2, 2, 1, 2,,1, k kk k mk Mwc m CrmnCrmn Mcr m mJ , (14) where k m is a weight parameter with respect to the scale m. After rescaling to for all m and n, the important edges can be identified in by comparing the absolute values of 2, k Crmn , k Wcm n , k Wcm n 2k Cr and . If k Wc m ,n 2,Crmn , kk Wc mn e at the point , we retain the value of at the point . We use a new matrix name ,n to represent the retained value, ,.n Making comparison at th 1 ,nn , km n d ne k new Wmn 2 n k w W ,Wc Wc i.e. 12 ,nnn k m m scale m for all points 12 12 ,1,nnn nnN ,mn 2, k Crmn , we identify which represents the most important features of the image edges. We set the values of and to 0’s at the positions identified and thus obtain a new set of and , k new Wmn ,m n 2 k Cr k k Wc ,Wcm n labelled as 2,Crmn k and , k Wc . Next we go to rescale and compare m n 2, k Crm n with , k Wcm n and extract the wavelet transform coeffcients that correspond to the next most important features of the image edges. We repeat this process until all major image Figure 1 shows edges are acquired. the effect of this wavelet transform filtering method at the scale m = 3 and 327 k mm . In this figure, (a) is the original Lena ima image containing Gaussian white noise with the standard deviation 35 ge, (b) is noised . 13,Wcn and 23,Wcn are given in Fic)ectivel gures 1( and (d), respy. 11 3, 4,WcnWcn and are shown in Figures 1 (f). Figures 1(g) and 2 4, n 2 3,Wcn Wc (e) and (h) present 13, new Wn and we acquire the fil- te 1 23, new Wn. By thentioneh, above med approac red dyadic wavelet transform data k 1 new mJ W 12 ,n, we can rec . Let on- k kk d 2 ,, new J WJnWJnWfn struct the filtered image from the set 12 ,, ,, J newnew 21 J Wj nWjnSnwhere Figure 1. The effect of the new wavelet filtering at the scale m = 3 and 327. k mm (a) The original Lena image; (b) the noised image; (c) W ( ; (h) 23 new Wn 13,cn; (d) 23,Wcn; (e) 11 3, 4,WcnWcn ; 3, nW; (g) ,. f) Wc 2 4,c n 2 13, new Wn Copyright © 2011 SciRes. JSIP  A Dyadic Wavelet Filtering Method for 2-D Image Denoising Copyright © 2011 SciRes. JSIP 311 thugh the inverse dyadic wav- elet transform. The fil Transform Filtering Algorithm for the discrete wavelet transform of no 12 2 11 ,, j k kd Jj Wjn Wfnn 12 22 , JJ SnS nn dfro J and 12 22 , JJ d SnSfnn tering algorithm is summarized as follows. Wavelet Step 2. Initialize: ,, kkk Wbm nWcmnWmn,, Image Denoising Step 1. Compute , k N Filterm nO kk , ised image 12 , xx and its the lower-frequency sm- oothed image: 2, ,1,,1 k CrmnWc mnWcmnmJ1 for iteration { Loop for the scale m Step 3. Loop 11mJ { 2 12 , max2 , kk nnn N crmCrm n ,,2, kkk k wc mWc mwhereCrmMcr m Loop for each pixel point 12 ,nnn { 2 kk Cr b, 2,kkk m m nCrm nMwcMcrm end loop n } Loop for each pixel point nn 12 ,n { If 2, , kk CrbmnWcm n 0 e m for the pixel 2, k Crmn ,0 k Wcm n k Filterm n,1 end if }end loop n }end loop m }end iteration Scale space filtering: Loop for the scal { Loop 12 ,nnn { k , velet coefficient at the maxi- m ,, kk new WmnFilterm n Wbmn } end loop n } end loop m Step 4. Compute the wa um scale : ,, kk new WJnWJn Step 5. Reconstruct the image fromed wavelet da filter ta k 1 , new J Wjn and Sn 2J The reco the set nstruction from k 21 ,,J new J WjnSn through the inverse dyadic wavelet transform will yi inverse dyadic wavelet transform that we implemented in our technique uses a trous algorithm and the quadratic spline scaling functions and wavelets given in [18]. Now we give some comments on the choice of the number of iterations and weight parameter k m . We can design wavelet filtering iteration times and parameter k m according to the user’s request. For thumber of iterations, when it is too small, we can not obtain a oth estimate. If the number of iterations is too large, most of the edge information of reconstructed image will e n smo eld the final filtered image. The  A Dyadic Wavelet Filtering Method for 2-D Image Denoising 312 be eliminated. Thus we should choose a tradeoff between the number of iterations and the estimation of filtered image. It is well known that the Lipschitz exponents of image and noise are different. At the finer scales such as 1 2 and 2 2, the modulus maxima mainly produced by noise, while at coarser scale, most modulus maxima duced image. So if we set the different value of k m pro by at the different scale m, noise will be eliminated more effectively. In general, let parameter k m be lager e larger scale. 4. Experimental Results at th We use Peak-Signal-Noise-Ratio Square-Error (RMSE) to evalua (PSNR) and Root-Mean- te restored results. PSNR and RMSE is defined by the following: 2 255 ,10log10 1 PSNRu w2 ,, , ijij ij uw mn (14) 2 ,, , 1 ,ijij ij RMSEuwuw mn , (15) where and denotes the pixel valu processed and the original images respectively. Hard- ldin sof entioned Lena im- ag presses more noise while preserves m sian noise with the standard de ,ij w,ij ues of the threshog and t-thresholding are widely used for denoising in image processing by many researchers. Therefore, in the following tests the hard-thresholding method, soft-thresholding method, Xu’s method and Zheng’s method will be used to compare with the dyadic wavelet transform filtering algorithm. Example 1: When we use our filtering method to do denoising experiment for the above m e corrupted by additive noise, the restored result is Figure 2(a). If apply softthreshold, hard-threshold, Xu’s method and Zheng’s method to filter the noised image, the result is in Figures 2(b)-(e). Table 1 presents the values of PSNR and RMSE for each of the schemes. From all the five restored images, it is clear that our proposed method sup ore fine details and small structures in the image. In addition, from the values of PSNR and RMSE for res- tored image, our method increases the PSNR by 1 - 3 dB and reduce the RMSE 5 - 6. Example 2: A texture image is used in the second test. It is added by the white Gaus viation 30 . Use our filtering method, soft-thr- esholding method, hard-thresholding method, Xu’s met- hod and Zmethod to process noised image, we can find that our method is also better than other four methods. Figure 3(a) is the original image, Figure 3(b) is the noised image. Figures 4(a)-(e) show the results 50 100 200 150 250 25020015010050 (a)Our method. 50 100 200 150 250 25020015010050 (b)Soft-threshold 50 100 200 150 250 250 200 150 100 50 (c)Hard-threshold. 50 100 200 150 250 250 200 150 10050 (d)Xu’s Method. 50 100 200 150 250 250 200 150 100 50 (e)Zheng’s Method. heng’s processed by the five methods. Figure 2. Filtered results. (a) Our method; (b) Soft-threshold; (c) Hard-threshold; (d) Xu’s method; (e) Zheng’s method. Table 2 is the comparison of the values of PSNR and RMSE for restored images. Copyright © 2011 SciRes. JSIP  A Dyadic Wavelet Filtering Method for 2-D Image Denoising313 Table 1. PSNR and RMSE for each of the schemes. threshold method method Method Our method Soft- threshold Hard- Xu’s Zheng’s PSNR 25.2035 dB 23.1125 dB 22.4597 dB 24.0583 dB23.1079 dB RMSE 14.6 17.19.15.0078203 2111 9818 17.8297 50 100 200 150 250 250 200 150 100 50 (a)Original image. 50 100 200 150 250 250200150100 50 (b)Noised image. Figure 3. Texture image. (a) Original image; (b) Noised image. 50 100 200 150 250 25200150100 50 (a)Our method. 0 50 100 200 150 250 250200150100 50 (b)Soft-threshold. 50 100 200 150 250 250200150100 50 (c)Hard-threshold. 50 100 200 150 250 250 200150 100 50 (d)Xu’s Method. 50 100 200 150 250 250 200150 100 50 (e)Zheng’s Method. Figure 4. Results for the texture image. (a) Our method; (b) Soft-threshold; (c) Hard-threshold; (d) Xu’s method; (e) Zheng’s method. od Soft-thresh old Hard-thresh old Xu’s method Zheng’s method Table 2. PSNR and RMSE for restored images. Method Our meth PSN74 dBR 24.1536 dB 22.5607 dB 22.5533 dB 22.3974 dB22.77 From ts ot visual ti r pr he results above, it is obviouthat nonly for quality of images, but u also for quantitative evalua- rdon of ocessi esimtored ages, o metho tuin texre ime ag ng is still better than other four methods. Example 3: We use a man image containing both a human face and some textures to do the third test. The challenge with this image is to keep both texture details and smooth transitions in the human face in the process- ing. We add the original image (Figure 5(a)) with the white Gaussian noise with σ = 30, and get a noised image (Figure 5(b)). Figures 6(a)-(e) are the results obtained by five methods 50 50 100 200 150 250 250 200150 100 50 (a)Original image. 100 200 150 250 250 200150 100 50 (b)Noisy image. Figure 5. Man image. (a) Original image; (b) Noisy image. 50 100 200 150 250 25 200150 100 50 (a)Our method. 0 50 100 200 150 250 250 200150 100 50 (b)Soft-threshold 50 100 200 150 250 250 200150 100 50 (c)Hard-thres hold. 50 100 200 150 250 250 200150 100 50 (d)Xu’s Method. 50 100 200 150 250 250 200150 100 50 (e)Zheng’s Method. Figure 6. Results for man image. (a) Our method; (b) Soft- threshold; (c) Hard-theshold; (d) Xu’s method; (e) Zheng’s method. RMSE 15.8075 18.9892 18.9966 19.3488 18.5212 Copyright © 2011 SciRes. JSIP 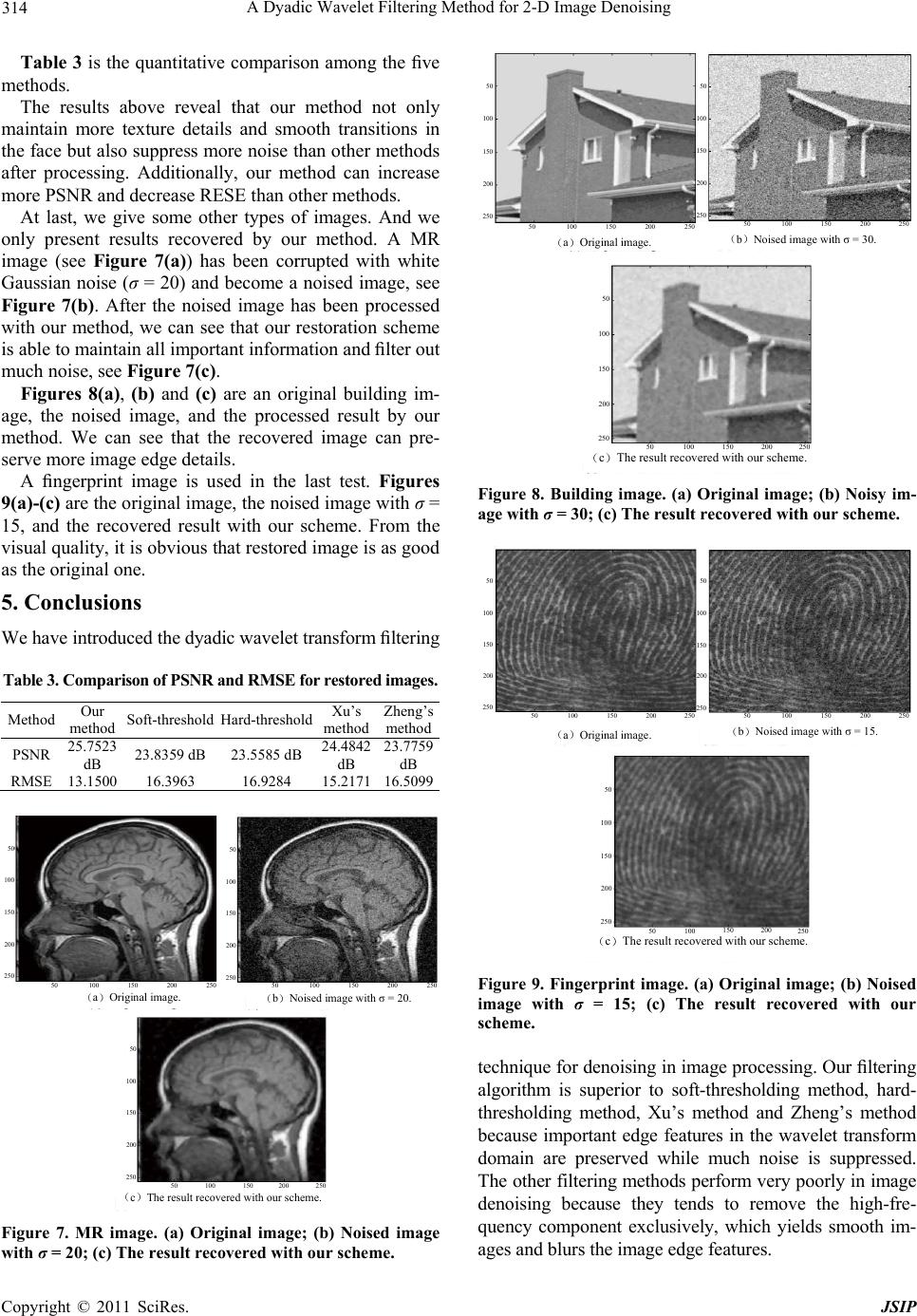 A Dyadic Wavelet Filtering Method for 2-D Image Denoising 314 Table 3 is the quantitative comparison among the five methods. The results above reveal that our method not only maintain more texture details and smooth transitions in the face but also suppress more noise than other methods after processing. Additionally, our method can increase more PSNR and decrease RESE than other methods. At last, we give some other types of images. And we only present results recovered by our mthod. A MR w aintain all important information and filter out m wavelet transform filtering method method e image (see Figure 7(a)) has been corrupted with white Gaussian noise (σ = 20) and become a noised image, see Figure 7(b). After the noised image has been processed ith our method, we can see that our restoration scheme is able to m uch noise, see Figure 7(c). Figures 8(a), (b) and (c) are an original building im- age, the noised image, and the processed result by our method. We can see that the recovered image can pre- serve more image edge details. A fingerprint image is used in the last test. Figures 9(a)-(c) are the original image, the noised image with σ = 15, and the recovered result with our scheme. From the visual quality, it is obvious that restored image is as good as the original one. 5. Conclusions We have introduced the dyadic Table 3. Comparison of PSNR and RMSE for res tored ima ges. Method Our method Soft-threshold Hard-threshold Xu’s Zheng’s PSNR 25.7523 dB 23.8359 dB 23.5585 dB 24.4842 dB 23.7759 dB RMSE 13.1500 16.3963 16.9284 15.217116.5099 50 100 200 150 250 50 250200150 ginal image. 100 (a)Ori 50 100 200 150 250 10050 (b)Noised 250200 = 20. 150 image with σ 50 100 200 150 250 25020015010050 (c)The result recovered with our scheme. 50 100 200 150 250 25020015010050 (a)Original image. 50 100 200 150 250 25020015010050 (b)Noised image with σ = 30. 50 100 200 150 250 250 200150 100 50 im- age with σ = 30; (c) The result recovered with our scheme. (c)The result recovered with our scheme. Figure 8. Building image. (a) Original image; (b) Noisy 50 100 200 150 250 25020015010050 (a)Original image. 50 100 200 150 250 25020015010050 (b)Noised image with σ = 15. 50 100 200 150 250 250 200150 100 50 (c)The result recovered with our scheme. Figure 9. Fingerprint image. (a) Original image; (b) Noised image with σ = 15; (c) The result recovered with our scheme. technique for denoising in image processing. Our filtering algorithm is superior to soft-thresholding method, hard- thresholding method, Xu’s method and Zheng’s method because important edge features in the wavelet transform domain are preserved while much noise is suppressed. The other filtering methods perform very poorly in image denoising because they tends to remove the high-fre- quency component exclusively, which yields smooth im- ages and blurs the image edge features. Figure 7. MR image. (a) Original image; (b) Noised image with σ = 20; (c) The result recovered with our scheme. Copyright © 2011 SciRes. JSIP  A Dyadic Wavelet Filtering Method for 2-D Image Denoising Copyright © 2011 SciRes. JSIP 315 6. Acknowledgements This work was supported by the Key Project of Ch Ministry of education (No. 109030), 382 Training Pr amme of CUC(G08382316), and Science Research Pro- ject of Communication University of China(XNL1003). The authors would like to thank the reviewers for ve useful comments, which improved the manuscript sig- nificantly. tiscale Edges,” IEEE Transactions on Pattern Analy- inese ogr- ry REFERENCES [1] S. Mallat and S. Zhong, “Characterization of Signal from Mul sis and Machine Intelligence, Vol. 14, No. 7, 1992, pp. 710-732. doi:10.1109/34.142909 [2] S. Mallat and W. L. Hwang, “Singularity Detection and Processing with Wavelets,” IEEE Transactions on Infor- mation Theory, Vol. 38, No. 2, 1992, pp. 617-643. doi:10.1109/18.119727 [3] J. L. Starck and A. Bijaoui, Filtering and Deconvolution by the Wavelet Transform,” Signal Processing, Vol. 35, No. 3, 1994, pp. 195-211. doi:10.1016/0165-1684(94)90211-9 [4] A. Bijaoui, “Wavelets, Ga Signal Processing, Vol. 82 ussian and Wiener Filter , No. 4, 2002, pp. 709-712. ing,” doi:10.1016/S0165-1684(02)00137-8 [5] P. L. Shui, “Image Denoising Algorithm via Best Wavelet Packet Base Using Wiener Cost Function,” Institution of Engineering and Technology Image Processing, Vol. 1, No. 3, 2007, pp. 311-318. [6] Y. Xu, J. B. Weaver, et al., “Wavelet Transform Domain Filters: A Spatially Selective Noise Filtration Technique,” IEEE Transactions on Image Processing, Vol. 3, No. 6, 1994, pp. 747-758. [7] C. Okechukwctive Noise Filtra- Image Denois eucom.2008.04.016 u and C. Ugweje, “Sele tion of Image Signals Using Wavelet Transform,” Imag- ing Measurement Systems, Vol. 36, No. 3-4, 2004, pp. 279-287. [8] M. Nasri and H. Nezamabadi-pour, “ing in the Wavelet Domain Using a New Adaptive Thresholding Function,” Neurocomputing, Vol. 72, No. 4-6, 2009, pp. 1012-1025. doi:10.1016/j.n 8, 2000, pp. 1535-1549. [9] Y. Zheng, D. B. H. Tay, et al., “Signal Extraction and Power Spectrum Estimation Using Wavelet Transform Scale Space Filtering and Bayes Shrinkage,” Signal Proc- essing, Vol. 80, No. doi:10.1016/S0165-1684(00)00054-2 [10] Y. Leung, J. S. Zhang and Z. B. Xu, “Clustering by Scale-Space Filtering,” IEEE Transaction on Pattern An- alysis and Machine Intelligence, Vol. 22, No. 12, 2000, , pp. 446- pp. 1396-1410. [11] J. Kalif, S. Mallat and B. Rouge, “Deonvolution by Thresholding in Mirror Wavelet Bases,” IEEE Transac- tion on Image Processing, Vol. 12, No. 4, 2003 457. doi:10.1109/TIP.2003.810592 [12] Y. F. Zheng and R. L. Ewing, “Feature-Based Wavelet Shrinkage Algorithm for Image Denoising,” IEEE Trans- action on Image Processing, Vol. 14, No. 1 2024-2039. 2, 2005, pp. y and Machine, Vol. 37, No. 4, 2007, pp. [13] Z. Y. Chen, X. P. Guo, X. L. Zhang, W. J. Cram and Z. W. Li, “A Novel Method for Analysis of Single Ion Channel Signal Based on Wavelet Transform,” Com- puters in Biolog 559-562. doi:10.1016/j.compbiomed.2006.08.006 [14] D. L. Donoho and I. M. Johnstone, “Ideal Spatial Adap- tion via Wavelet Shrinkage,” Biometrika, Vol. 81, No. 3, 1994, pp. 425-435. doi:10.1093/biomet/81.3.425 [15] D. L. Donoho, “De-Noising by Soft-Thresholding,” IEEE Transaction on Information Theory, Vol. 41, No. 3, 1995, pp. 613-627. doi:10.1109/18.382009 [16] M. Holschneider, R. Kronland-Martinet, J. Morlet and P. of 8th Tchamitchian, “Wavelets, Time-Frequency Methods and Phase Space, Chapter A Real-Time Algorithm for Signal Analysis with the Help of the Wavelet Transform,” Springer-Verlag, Berlin, 1989, pp. 289-297. [17] A. Witkin, “Scale Space Filtering,” Proceedings International Joint Conference on Artificial Intelligence, Karlsruhe, 1983, pp. 1019-1022. [18] S. Mallat, “A Wavelet Tour of Signal Processing,” 2nd Edition, Academic Press, New York, 1999.
|