 Journal of Environmental Protection, 2011, 2, 1172-1191 doi:10.4236/jep.2011.29136 Published Online November 2011 (http://www.scirp.org/journal/jep) Copyright © 2011 SciRes. JEP Robust Resource Management Control for CO2 Emission and Reduction of Greenhouse Effect: Stochastic Game Approach Bor-Sen Chen*, Ying-Po Lin Lab of Control and Systems Biology, National Tsing Hua University, Hsinchu, Taiwan (China). Email: *bschen@ee.nthu.edu.tw, d947920@oz.nthu.edu.tw Received August 10th, 2011; revised September 15th, 2011; accepted October 21st, 2011. ABSTRACT With the increasingly severe global warming, investments in clean technology, reforestation and political action have been studied to reduce CO2 emission. In this study, a nonlinear stochastic model is proposed to describe the dynamics of CO2 emission with control inputs: clean technology, reforestation and carbon tax, under stochastic uncertainties. For the efficient resources management, a robust tracking control is designed to force resources tracking a desired refer- ence output. The worst-case effect of stochastic parametric fluctuations, external disturbances and uncertain initial conditions on the tracking performance is considered and minimized from the dynamic game theory perspective. This stochastic game problem, in which one player (stochastic uncertainty) maximizes the tracking error and another player (control input) minimizes the tracking error, could be equivalent to a robust minimax tracking problem. To avoid solv- ing the HJI, a fuzzy model is proposed to approximate the nonlinear CO2 emission model. Then the nonlinear stochastic game problem could be easily solved by fuzzy stochastic game approach via LMI technique. Keywords: CO2 Emission System, Dynamic Game Theory, Greenhouse Effect, LMI, Resource Management Control, Robust Tracking Control, T-S Fuzzy Model 1. Introduction In recent years, the world has attracted much attention to environmental issues such as atmospheric pollution, con- servation of water reserves and the reduction of tropical forests cover. For example, people feel concern about glo- bal warming, caused by greenhouse gases (GHG) such as carbon dioxide (CO2), methane, nitrous oxide, sulfur he- xafluoride, hydrofluorocarbons and perfluorocarbons, which leading to ecological destruction, climatic anomalies and sea level rise [1-2]. However, despite the increasing en- vironmental awareness, global economic success heavily relies on the industrial throughput. People have gained a better life following the expansion of industrial sector and the number of job positions. This has been achieved following the expresses of urban environmental quality, significant increase in pollution, and loss of natural ha- bitats [3]. In order to reduce the emissions of GHG, espe- cially CO2, without limiting economic growth, substan- tial investments should target the development of clean technology, expansion of forested areas and some politi- cal actions [4-6]. A major problem associated with economic growth is the need for the energy, for which fossil fuel is the pri- mary source. Such economic growth resulted in an in- crease of atmospheric emission of CO2, as shown in Ta- ble 1 [7]. From Figure 1 [8], it is seen that from 1900, the global CO2 emission increased year by year except in the European Union (EU) that decreased by 2% in the later period (1990-1996), but it is still very high else- where. According to United Nations Environment Pro- gramme (UNEP) in 2007 [7], this decrease was possible due to many initiatives taken by Germany such as in- vesting in renewable energy, solar power, new techno- logy for car production, reforestation and political ac- tions creating laws requiring 5% reduction of carbon emission. Recently, an indicator called the Ecological Footprint (EF) was concerned by UNEP to relate the ‘pressure’ exerted by human pollutions on the global ecosystems (Table 2) [7]. The EF is expressed in terms of area, and according to the definition provided by WWF [9], it represents “how much productive land and sea is needed to provide the resources such as energy, water and raw materials used everyday. It also calculates  Robust Resource Management Control for CO Emission and Reduction of Greenhouse Effect: 1173 2 Stochastic Game Approach Figure 1. Global carbon emission. The CO2 emission has an increasing trend in the world, except for an about 2% decreasing in recent period (1990~1996) in EU. Table 1. Carbon dioxide emission by region (1998). Region Million tones carbon/year Asia and Pacific 2167 Europe 1677 North Amer ica 1614 Latin America & Caribbean 365 West Asia 187 Source: UNEP (2007). Table 2. Ecological footprints. Region Hectares/ per capita Africa <2 Asia and Pacific <2 Latin America & Caribbean Between 2 and 3 West Europe Between 4 and 5 North Amer i ca >11 Source: UNEP (2007). the emission generated from the oil, coal and gas burnt, and determines how much land is required to absorb the waste”. This indicator is very useful in establishing how far the present situation is from the ideal condition in terms of emission of CO2. The worst EF indicators are found in North America and Western Europe. In order to mitigate the threat of an escalating greenhouse effect, it is necessary to establish a rigorous management process of the available resources to reduce CO2 emission. These should include direct government incentive to promote pro-environment actions by the private sector and the establishment of stricter pollution regulations. To meet the CO2 emission limitations and combat global warming, 193 parties (192 states and the EU) have signed and rati- fied the Kyoto Protocol to the United Nations. Framework Conventio n on Climate Change (UNFCCC) [10]. The cost estimated for the industrialized countries to implement the Kyoto Protocol ranges from 0.1 to 0.2% of their gross domestic product (GDP) [3]. Based on mathematical dynamic models, these costs can be efficiently optimized through control theory methods. In order to manage the resources commit ment to achi- eve the desired control of CO2 concentration, mathe- matical models are required. In previous studies, Nord- bous (1991) [11,12] presented a mathematical model to describe the effect of GHG in the economy and to maxi- mize a social welfare function, subject to dynamic con- straints for the global temperature and atmospheric con- centration of CO2. He carried out a study considering low, medium and high level of damages as a function of the concentration of CO2. In another study, Nordhous (1993) [13] used the same mathematical model to evalu- ate optimal taxation policies to stabilize climate and car- bon emissions, i.e. enforcing political actions about taxes on the CO2 emissions from burning coal, petroleum based products and natural gas. Poterba (1993) [14] has discussed the relationship between global warming and GDP growth and considered the influence of certain macro- economic initiatives on the decrease of the atmospheric emission of CO2. For example, a consumption-linked carbon tax to reduce CO2 emissions by 50% would re- duce GDP by 4% in North America, 1% in Europe, and by 19% in some oil exporting countries. In the study of Copyright © 2011 SciRes. JEP  Robust Resource Management Control for CO Emission and Reduction of Greenhouse Effect: 1174 2 Stochastic Game Approach Stollery (1998) [15], an optimal CO2 emission tax could be initially high, but it would eventually be lowered as emission decline due to energy resource depletion. He also showed that to sustain consumption in the face of both energy resource depletion and economic damage from global warming, it suffices to reinvest the sum of carbon tax revenues and the net energy rents. Caetano et al. (2008) [3] follows the ideas in Stollery [15] and offers a quantitative tool for the efficient allocation of resour ces to reduce the greenhouse effect caused by CO2 emission. Their approach was developed by a mathematical model to describe the dynamic relation of CO2 emission with investment in reforestation and clean technology, and propose a method to efficiently manage the available resources by casting an optimal control problem. Also an optimal tracking control of CO2 emission was addressed to achieve the emission targets proposed in the Kyoto Protocol for European countries by numerically solving a Hamiltonian function [16]. In the above methods, ordinary nonlinear differential equations with time-invariant parameters are used to de- scribe the deterministic dynamics among CO2 emissions, forest area expansion and GDP growth. However, these intrinsic parameters may fluctuate area to area and time to time for different regional development or unpredict- able situations, like su b-pr ime crash that in itiated in 200 7, which may lead to the necessity of estimating new pa- rameters as time or let the control strategies be li mited in some specific area. Further, the external disturbances, due to modeling error and environmental noise, should also be considered in order to mimic the real dynamics of CO2 emission system. Therefore, the dynamical model of CO2 emission system should be described by stochastic differential equations (SDEs). A differential equation containing a deterministic part and an additional random fluctuation term is called a stochastic differential equa- tion, which has been frequently used to model diverse phenomena in physics, biology and finance [17]. In this study, a nonlinear stochastic model is proposed to des- cribe the dynamic system with model uncertainties from intrinsic parametric fluctuations, for the CO2 emission with investments in reforestation, clean technology and political action about carbo n tax. In add itio n to the in trin- sic parametric fluctuations, external disturbances from modeling error and environmental noise are also in- cluded in the nonlinear stochastic model of CO2 emission system, thus the generalized dynamic model could be widely applied to different area and time. Then a refer- ence model is developed to generate the desired dynam- ics of CO2 emission system. Finally, a robust model ref- erence tracking control is proposed to manage these available resources, so that the nonlinear stochastic CO2 emission system can track the desired output of the reference model, in spite of parametric fluctuations and external disturbances [18,19]. Since the statistical know- ledge of the parametric fluctuation, external disturbance and uncertain initial condition is always unavailable, based on robust H∞ control theory, the worst-case effect of parametric fluctuations, external disturbances and un- certain initial conditions on the tracking error should be minimized by the control efforts, so that all possible ef- fects on the desired reference tracking, due to these un- certainties, could be attenuated as small as possible. The parametric fluctuations, external disturbances and uncertain initial conditions are considered as one player to maximize the tracking error, while the control of re- source management is considered as another player to minimize the tracking error, from the dynamic game (minimax) theory perspective. This stochastic game pro- blem could be equivalent to a robust minimax tracking problem, to achieve a prescribed reference output, in spite of the worst-case effect of parametric fluctuations, external disturbances and uncertain initial condition. Thus, solving the stochastic game problem for nonlinear stochastic CO2 emission system will need to solve the Hamilton Jacobi inequality (HJI). At present, there is no analytic or numerical solution for the HJI except simple cases. To avoid solving the HJI for the nonlinear sto- chastic game problem, a Takagi-Sugeno (T-S) fuzzy model [20] is proposed to interpolate several linearized stochastic systems at different operation points, to ap- proximate the nonlinear dynamics of CO2 emission sys- tem. With the help of fuzzy approximation method to simplify the nonlinear stochastic game problem, it can be easily solved by the proposed fuzzy stochastic game ap- proach via linear matrix inequality (LMI) tech nique with the help of Robust Control Toolbox in Matlab. Finally, some simulation results are given to confirm the robust minimax tracking performance of the proposed stochas- tic game approach for reducing the CO2 emissions and greenhouse effect. Mathematical Preliminaries: Before the further analysis of the stochastic CO2 emis- sion system, some definition and lemma of SDE are given in the following for the convenience of problem description and control design: Definit i on 1 (Ito SDE) [ 17] : For a given stochastic differential equatio n taxt bxtnt where t is a stochastic process; axt and bxt are functions of t; is the standard white noise with zero mean and unit variance to denote the random fluctuation, which can be considered as the nt C opyright © 2011 SciRes. JEP  Robust Resource Management Control for CO Emission and Reduction of Greenhouse Effect: 1175 2 Stochastic Game Approach derivative of Wiener process (or the Brownian motion). The Ito type stochastic differential equation (Ito SDE) of t dw t is represented by dx tax tdtbxtdwt where denotes the standard Wiener process, i.e. . wt n tdt Lemma 1 (Ito’s formula) [21,22]: Let t be an Ito stochastic process in the above equation, if is a twice continuous differen- tiable function of :f t, then xt is also a sto- chastic process satisfied with the following dynamic equation 1 2 T dfx tfx tdXt bxtfxtbxtdt 2. Stochastic Model of CO2 Emission under Parametric Fluctuation and External Disturbance For the convenience of illustration, some ordinary non- linear differential equations [3,16] has been proposed to model the dynamics of CO2 emission. Taking account the political actions mentioned in the previous section, the modified equations by introducing a carbon tax con- trol term are used [23,24]. The more general determinis- tic model deals only with a few parameters to represent the dynamics of atmospheric CO2 , forest area t zt and GDP t as follows [3,16] 112 1 3 1t trtzt uyt s ztuythzt ytyt ut 2 (1) The first Equation in (1) is to model the CO2 emission, in which 1 is the emission rate, r is the carrying ca- pacity of the atmosphere in terms of CO2, 1zt de- notes the removal of CO2 from the atmosphere and is proportional to total forest area , and 2 denotes the production of CO2 due to GDP. It is assumed that CO2 emission increases with the economic activity term zt t 12 uy 2 t and decreases with the clean technology investment term , which are both proportional to the GDP 2 uyt t. The second Equa- tion in (1) is to model the total area of forest, which de- pends on the reforestation term 1 uy and the forest depletion term . Consider the impact of economic activity is much larger than natural growth, the reforesta- tion term is assumed be a fraction of GDP, i.e. with laws and incentive to promote reforestation, whereas the total area of forest decreasing is mainly due to forest logging or other economic activities. The coefficient 1 repre- sents the intensity of incentives directed to reforestation and the coefficient represents the forest depletion rate, which amalgamates a variety of factors such as ex- pansion of cattle ranching, fire, commercial logging, shifted cultivators and colonization, among others. The third Equation in (1) is to model the GDP. Usually the t thz u h t is assumed to present an exponential growth with rate and 3 is a tax rate which is proportional to the CO2 emission, thus the CO2 revenue term u t 3 u u in- cluding the effects of carbon tax and “virtual tax”—all the effects that are similar to carbon tax, i.e. energy cost rise, consumer prices rise, real wages fall and output and employment fall [25] that can also be directly or indi- rectly controlled by government order. In (1), 1, 2 and 3 are control variables to be specified, so that the state variables u u t , zt and t can achieve their desired reference outputs. The above model has some limitations such as 1) the deterministic nature of economic growth (as expressed by GDP), 2) difficulty in limiting the geographic area, as one country, in political sense, can effect a neighboring state, 3) absence of time-varying parameters to adapt the model to changing situation. Further, the model is too simple and some factors may be neglected, i.e. there ex- ist some un-modeled dynamics. In order to mimic the stochastic dynamics of CO2 emission, the parameter fluctuations and external disturbances should be consid- ered in the following stochastic model 1 t 1t ut h h u 1 2 t s y zt t tt 12 33 t v v t v tr u t 11 yt 22 r yt 1 z t zt yt (2) where 1 r , 1 , 2 , h and denote the pa- rametric fluctuations of the coefficients, from one coun- try to one country and from time to time to adapt the model to changing situation. 1 vt , 2 and v t t 3 denote to the external disturbances, due to modeling er- ror and environmental noise. v Suppose the parametric fluctuations can be separated into a deterministic part and a random part as follows: nt 2 ,,nt nt 11 rn hn 1 45 2 3, , t t (3) where i denotes the standard deviation of stochastic parametric fluctuation, and denotes a standard white noise with unit variance, i.e. nt 2 11 var r , Copyright © 2011 SciRes. JEP  Robust Resource Management Control for CO Emission and Reduction of Greenhouse Effect: 1176 2 Stochastic Game Approach 2 1 var 2 nt and so on, i.e. the stochastic property of parametric fluctuations is absorbed by a white noise , and the amplitudes of parametric fluctuations are determined by their standard deviations i respectively. Then the stochastic model for dynamics of CO2 emission could be represented by 1122 1 3 12 1 4 5 1 1 tzt utyt s ut ythz ytu t tztt vt s zttv t ytv t 3 t t y n 2 3 rt t zt yt (4) For the convenience of analysis and design, the above stochastic CO2 emission system can be represented by the following Ito stochastic system [17,26] 112 11 22 3 3 123 4 5 1 00 00 00 1 t rtzt yt s dt dz t dy t wt hz tdt y t ut ytv t ut ytv tdt tvt ut t tztyt s zt dwt yt dt (5) where with dw tn tdt denotes a standard Wiener process or Brownian motion. Actually, the sto- chastic system for CO2 emission in (5) can be extended to a more general stochastic CO2 emission system as follows 0 , fx tgxtu ttdt hxtdwt 0 dx t xx v (6) where T 1n tx 1 vtv t txt T n v t , , denote the state vector, control T m uttu t 1 u input vector and external disturbance vector respectively. 1n xt R denotes the nonlinear interaction vector among the state variables of the CO2 emission system. nm xt R denotes the control input matrix. 1n hxtR denotes the noise dependent parameter fluctuation vector. In the more general model of (6), let 1 tt , 2 tzt, 3 tyt and so on. Consider a reference model of the stochastic CO2 emission system in (6) with a desired state output as fol- lows rrr tAxtrt (7) where 1n r tR nn is the reference state vector, r R is a specific asymptotically stable matrix and rt is a desired reference signal. Based on the model reference tracking control, r and rt are specified beforehand by designer, so that r t can represent a desired system’s state output for the stochastic system of CO2 emission in (6) to follow. Then, the robust model reference tracking control is to design to make ut t in (6) track the desired r t, such that the track- ing error r tx txt must be as small as possi- ble, in spite of the influence of stochastic parametric fluctuations, external disturbances and the uncertain ini- tial condition 0x in (6). Since the parametric fluctua- tions are stochastic, external disturbance and ini- tial state vt 0x are uncertain, and reference signal rt could be arbitrarily assigned, the robust model reference tracking control design should be specified, so that the worst-case effect of three uncertainties , vt 0x and rt on the tracking error t and control effort should be minimized and below a prescribed value ()ut 2 , i.e. both the minimax tracking and robustness against uncertainties vt , 0x, and should be achi- eved simultaneously as following stochastic game pro- blem rt 0 , 0 2 min max00 ,0 f f tTT t ut TT T vt rt ExtQxtutRutdt Evtvtrtrtdtxx x (8) where denotes the expectation, and the weighting matrices and are assumed diagonal as follow E Q R 11 11 22 22 00 0 00 , 00 00 00 nn mm qr qr QR qr 0 The diagonal element of denotes the punish- ii q Q C opyright © 2011 SciRes. JEP  Robust Resource Management Control for CO Emission and Reduction of Greenhouse Effect: 1177 2 Stochastic Game Approach ment on the corresponding tracking error and the diago- nal ii of denotes the relative control cost. r R2 denotes the upper bound of the stochastic game problem in (8). Since the worst-case effect of vt, rt and on the tracking error 0x t is minimized by con- trol effort , from the energy point of view, the sto- chastic game problem in (8) is suitable for a robust minimax tracking problem in which the statistics of , ut vt t vt and are unknown or uncertain, that are always met in practical control design case, for ex- ample, in the stochastic CO2 emission system. rt rt Remark 1: If and are all deterministic, then the ex- pectation in the den ominato r of (8) can be ne gl ec ted. E Because it is not easy to solve the robust minimax tracking problem in ( 8) subject to (6) and (7) directly, an upper bound 2 of the minimax tracking problem is proposed to formulate a sub-optimal minimax tracking problem. After that, the sub-optimal minimax tracking problem is solved firstly, then the upper bound 2 is decreased as small as possible to approximate the real robust minimax tracking problem of the stochastic CO2 emission system. Since the denominator in (8) is independent of ut t t and is not zero, equation (8) is equivalent to [27] mi ut min mi ut ut m vt , a m r vt Ju , ax r t , x ax t rt t 22 , TT T t u vt x 00 T Qxt vt x t Qxt vt 0 tRu rt TT tRu rt t T t rtd t rtd 0 2 f t Ex Ex 0 , f t t v Ex ,, n m n vt v (9) Let us denote 22 , TT t r t u vt (10) From the above analysis, the stochastic game problem in (9) or (10) is equivalent to finding the worst-case distur- bance and reference signal which maxi- mize r ut v t rt, and a minimax tracking con- trol which minimizes ut ,, ut v t r t, such that the minimax value ,, ut vt rt is less than , i.e. 0 T x 0 2Ex n , ax r t T ,, , 00 , , min 0 ut m vt 2 mi ut ,, utvtr Jut x t ut vt x J rt vtrt Ex (11) ut , vt g proble If there exist and such that the robust minimamsolved, then they can satisfy the stochastic game problem in (8 well. Therefore, the first step of robust minimax tracking control design of stochastic CO2 emission system is to song miax tr prob rt , in (11) is x trackin) as lve the followi nimackinglem , min max,, ut vt rt ut vt rt (12) subject to the CO2 emission system (6) and the desired reference model (7). After that, the next step is to check whether the condi- tion 2 ,, 00 T Jutvtr tExx not for any is satis- 0x . fied or To solve the minimax tracking problem in (12), it is convenience to transform the problem into an equivalent minimax regulation problem. Let us denote ,,, r rr , 00 fxt tvt xtxtvtF trt Ax t gxt hxt G Hxt xt thus an augmented stochastic system of (6) and (7) is obtained as follows (13) 0 0xx , dx tFx tGxtutCv tdt Hxt dwt (14) where 0 0 I C . Then the minimax tracking problem in (12) can writen as the following minimax regu lation problem be re- 0 minmax , 0 ut vt Ex tQxtutRut vtvtdt x 2 minmax , f vt tTT T Jut vt (15) subject to (12) where ut QQ QQQ . Then the robust minimax tracking problem in (11) is equivalent to the following constrained minimax regula- tion probl e m Copyright © 2011 SciRes. JEP  Robust Resource Management Control for CO Emission and Reduction of Greenhouse Effect: 1178 2 Stochastic Game Approach 2 00 T Ex Ix subject to (14) 2 0 ax f tTT T ExtxtutRut vtvtdt (16) where minm ut vt Q I I I . Theorem 1: The stochastic game problem in (16) for robust track- ochastic CO2 emission system could be llowing minimax tracking control ing control of st solved by the fou and the worst-case disturbance v 1 1TVxt utRGxt 2 t (17) 2 1 2 TVxt vt C t8) where (1 0Vxt is the positive solution of t ing HJI he follow- 2 2 2 1 4 1 4 10 2 T T T T T Vxt FxtxtQxt xt Vx 1 T T t Vxt GxtR Gxt txt Vxt Vxt CC xt xt Vxt Hxt Hxt xt (19) with 2 00 T EVxE xIx 0 (20) Proof: See Appendix A. Since 2 in cont is the upper bound of minimax tracking problem (8), based on the an alysis abov e, the minimax rol and the worst-case disturbance tracking ut vt still neednimize the upper b to miound 2 as follows 00 min Vxt 22 (21) subject to (19) and (20) After solving a and 2 0 Vx from the constrained optimization in (21), the solution Vx is substed into (17)titu to obtain the robuimax tracking control , for the stochastic CO2 ve the robust minimax tng of the desired re- spite of stochastic intrinsic pa- ra and l d st min emis racki ut achiesion system in (6), to ference model in (7), in metric fluctuationexternaisturbance. Remark 2: If in (8), i.e. the effect of vt , rt and 0 on tracking error t and control effort ut is neglected in the tracking design procedure. Then the ro- bust minimax tracking problem in (8) is reduced to the following optimal tracking problem [21,28,29] f tTT t 0 min ut ExtQxtutRudt (22) In this case, the optimal tracking control ut is also given by (1 7), i.e. 1 1 2 TVxt utRGxt t . How- ever, Vx in (17) should be replaced via so following HJI lving the 2 2 1 10 2 T T Vxt FxtxtQxt 1 4 T T Vx t Vxt GxtR Gxt T xt txt Vxt Hxt Hxt xt which is obtained from (19) but with (23) . Ther efore, if uivalent effect of e in the robust minimax trackle eq to the optimal tracking probse the xternal disturbance ing prob lem. Becau m, it is vt is neglect ance will b ed by the oping, its tracking performe dete- ri the external disturbance timal track orated by vt and uncertain initial condition 0 . Therefore, it isuitable for robnimax tracking design. 3. Robust Minimax Tracking Control via Fuzzy Interpolation Method In general, there is no analytic or numcal solution for the HJI in (19) to solve the constrained optimization problem in (21), for robust minim s not ust mi eri ax tracking control of the ate theeral linearized of robust minimax tracking control of stochastic CO2 the stochastic CO2 emission system in (6). Recently, T-S fuzzy model has been widely applied to approxim nonlinear system via interpolating sev systems at different operation points [18-20]. By the fuzzy interpolation method, the nonlinear stochastic game problem could be transformed to a fuzzy stochastic game problem so that the HJI in (19) could be replaced by a set of linear matrix inequalities (LMI). In this situation, the nonlinear stochastic game problem in (8) could be easily solved by fuzzy stochastic game approach for the design C opyright © 2011 SciRes. JEP  Robust Resource Management Control for CO Emission and Reduction of Greenhouse Effect: 1179 2 Stochastic Game Approach t minimax tracking control to achieve a de emission system. Suppose the nonlinear stochastic CO2 emission system in (6) can be represented by T-S fuzzy model [20]. The T-S model is a piecewise interpolation of several lin- earized models through membership functions. The fuzzy model is described by fuzzy if-then rules and will be employed to deal with the nonlinear stochastic game problem for robus sired CO2 emission, under stochastic fluctuations, ex- ternal disturbances and uncertain initial conditions. The i-th rule of fuzzy model for nonlinear stochastic system in (6) is of the following form [1 8,19] If 1 zt is 1i and ……and g zt is ig , then , 1 iii dxtAxtButCvt dtDxtdwtiL (24) where ij is the fuzzy set, i , i B and i D are lin- earized system matrices, is the number of premise variables and 1 zt, … g zt are the premise variables. The fuzzy system in (24) is inferred as fo lws [18-20] lo 1 ii i i i 1 () ii i i i i1 L i L L xtButCvt dtDxtdw dx zt t zt (25) where t hAxtButCvt dtDxtdwt zt 1 1 1 , ,, gi iiji L j i i T g zt ztFzthzt zt ztz tzt , and ij j zt is the grade of membership of j zt in ij . We assume and . There- fore, we get and (26) e T-S fue ne ems in (2pproximate linear stochastic system in (6) via the fuzzy basis - We could specify parameters A, B Di easily in (25), so that 0 izt 10 L i i zt 0 i hzt 1 1 L i i hzt . Thzzy model in (25) is to interpolat li- L func and ar stochastic syst4) to a the non- tion i hzt. i i 1 L ii i h t i hzt ztB and 1 L i i Axt , 1ii i hztDxt can approximate the nonlinear funcions L xt , xt and in (6), respectively, by mark 3her interpolatioethods suc n be also empled to interp several linear stochastic systems to approximate the nonlinear stoch bases hxt Fuzzy identification metho d [20] Re: Actually, in (25), otn mh as cubic spline method, caoyolate astic system in (6), i.e. the smoothing hzt fther i i oerpolat ithods. After the nonlinear stochastic could be replaced by other interpolation bases onton me system in (6) is ap- prhe T-S fuzzy system in (25), the aug- moximated by t ented system in (14) can be also approximated by the following fuzzy system L ii i i dx thztAxtButCv tdtDx tdwt (27) 1i where 000 ,,, 000 00 iii iii r ABc D ABCD AI . After the nonlinear augmented stochastic system in (14) is approximated by the T-S fuzzy system in (27), the nonlinear stochastic game problem in (14) and (16) replaced by solving the fuzzy stochastic game problem in (27) and (16). Theorem 2: minimax tracking control and worst-se distur- bance for fuzzy stochastic game problem in (16) subject to is The ca (27) are solved respectively as follows 1 2 1 1 , LTT jj j uthztRB PxtvtC Pxt (28) where P is the positive definite symmetric solution of thccati-like inequalities e following Ri 1 10; TT iiij TTT PAAPQPB RBP PCCPDPDi 2 2 , 1 ij jL PI (29) f: the HJI in (19) is approximated by a set of algebraic inequalities in (29) and the inequality in (20) is also equ ivalent to the second inequality in (29). Since Proo See Appendix B By fuzzy approximation, obviously, 2 is the upper bo minimax tracking problem8), the robust m tracking problem still needimize und of inimax in ( s to min2 as follows 22 0 min P 0 (30) subject to (29) In order to solve the above constrained optimization problem in (30) by the conventional LMI method, the inequalities in (29 ) can be rewritten as following relax ed conditions [30] Copyright © 2011 SciRes. JEP  Robust Resource Management Control for CO Emission and Reduction of Greenhouse Effect: 1180 2 Stochastic Game Approach 1TT iiii PAAPQPBRBP 2 2 1 0; 22 TT T ii ij ij PC C PDPD DD DD Pij PI Then, we let , and the inequalities in (31) can be equivale 1 2 1 TT TT iii j T PA APQPBRBPPCCP (31) 0; i j 10WP nt to 1 1 2 2 2 10; 1 1 10; 22 TT ii ii TT ii TT ii ij T T j AWWAWQWB RB CCWD WDWij AWWAWQWB RBCC W Wij WI or iij DD DD W 1 1 2 1 2 1 2 10; 1 0; 22 TT T ii ii TT ii TTT T ii ij T ijij AWWAWQQWBRB CCWD WDWij AWWAWQQWBRBCC DD DD WW W WI ij where 11 22 QQQ . By the schur complement [27]. The constrained opti- mization problem in (30) is equivalent to the following LMI-const rai n ed opt imizati on pr oblem 22 00 min W (32) subject to 1 2 00 ; TTTTT iiiii i AWWAB RBCCWDWQ DWWij 1 2 2 1 2 00; 2 0 T ij T DD TT T iiij ij AW WAB RBCCWWQ DDWWij QW I WI (33) Remark 4: 1) The fuzzy basis functionin (25) can be replaced by other interpolatin, for example, cubic spline function. 2) By fuzzy approximation, the HJI in (19) of nonlin- ear stochastic game problem for the robust minimax tracking of nonlinear stochastic CO2 emission system is replaced by a set of inequalities in (29), which can be easily solved by LMI-constrained optimization in (33 rained optimization to solve i hzt on functio ). 3) The const0 and in ed byW (32), (33), can be easily solv decreasing 2 until there exists no 0W solution in (32), (33). 4) After solving W an1 d then from the con- str PW ained optimization problem in (32), (33), 0 can be solved by Robust Control Toolbox in Matlab efficien tly. 5) If the conventional optimal tracking control in (22) is considered, i.e. the effect of disturbance vt is not considered in the control design problem, then the opti- m to lettingal tracking control problem is equivalen 2 t in (8). The optimal fuzzy tracking control desi gn 1jj j thztR Pxt can ved by a com- mon positive definite symmetric matrix P from the inequ 2 1 L u T Bbe sol alities in (29) with , i.e. solving a common positive definite symmetric matrix 0P fromthe fol- lowing inequalities [27] 10; ,1 TT iiiji j PAAPQPB RBPDPD ij L (34) or the following relaxed conditions [30] 1 1 0 TTT iiiii i TT iiij T ij PAAPQPB RBPDPDij PAAPQPB RBP DD 1 0QW I ; 0; 22 ij DD Pij In order to solve the optimal tracking problem by LMI s equivalent to technique, the optimal tracking control i solving a common 1 WP from the following inequali- ties, C opyright © 2011 SciRes. JEP  Robust Resource Management Control for CO Emission and Reduction of Greenhouse Effect: 1181 2 Stochastic Game Approach 11 1 1 0; 0; 22 TT TT ii iiii TT T ii ij T ijij WWAWQIQW BRBWDWDWij AWWAWQIQWBRB DD DD WW Wij or following LMIs, 1 1 00; 0 2 00; 2W 0 i i T ij TT T iiij ij B DWWi j QW I DD AWWAB RBWWQ DD W ij QW I TTTT iii i AWWAB RWDWQ (36) i.e., ifis solved from (36), then the optimal fuzzy t control ca n be o bt ai ned as 1 WP racking 1 1 LT jj j ut hztRBPxt According to the analysis above, the robust minimax tracking control of CO2 emission system via fuzzy inter- polation method is summarized as follows. Design Procedure: Step 1. Give a desired reference model in (7) for the c CO2 and construct fuzzy plant rules in (24) and (25). Step 3. Give the weighting matrices and of minimax tracking problem in (8). stochasti emission system in (6). Step 2. Select membership functions Q R Step 4. Solve the LMI-constrained optimizatio n in (32 ), (33) to obtain W (thus 1 PW ) and 2 0 . Step 5. Construct the robust minimax tra cking control Control Toolbox inly. 4. Cm ers aren to fit th to eme influence of disturbances on the CO2 emm, the bounded standard deviations are as t in (28). u Remark 5: The software packag e such as Robu st Matlab can be employed to solve the LMI-constrained optimization problem in (32), (33) easi Computational Simulation onsider the stochastic CO2 emission system in (5). The values of systeparamet given iTable 3 e actual CO2 emission in Western Europe [3]. In order phasize th ission syste sumed that 11 r , 21 , 32 , 4h , 5 , i.e. Table 3. Model parameters for Western Europe [3]. Parameters Valu the standard es deviations of parametric fluctuations are r1 0.15 s 700 h 0.0001 u1 0.00012 u2 0.0008 u3 0 α1 0.0006 γ 0.035 α2 0.00005 equal to the original system parametersis a stan- dard Wiener presses with unit variae environ- mental dists ; ()wt h ofnce. T urbance 13 ~vtvt he conven arnown but bounded signls. For ttionalulation, e unk of sima 13 ~vtvt with varian To simulate rope, the in are assumro noise c to and pectively. e dynamssiou- itial valui ed to be ze 3 10 , 2 10 ic CO2 emi es in 1960 are g mean white es equal4 01, res thn in Western E ven as 398t illion m3 87 billion rol efforts million to of conifer ternationa nes O2 st ar l dollars of of C emission [7], ea [31,32] and GDP [33-35 zt ]. 43 m cont to fore 27yt in The were assumed to be invariant from 1960 2010, i.e. 10.00012u , 20.0008u , 30u, to fit the actual data [3] (Figure 2). But these conro l efforts would limit the system behavior too rigid for actual performance hich could not guarantee th e control ability of CO2 emission under distan (Figur ). In order to attenuate the effect of stochactic disturbance on CO2 emission system and make a flexible control desir actual demand immediately, the robuax tracking control method will be applied after 20 For the robust minimax tracking control purpose, the reference model design requests a prescribed trajectory C. Thus, the system ma- trix r demand, wurb cese 3 gn fo st minim 10. behavior forO2 emission system stant cont and reference signal rt should be specified, based on some standards in prior, to determine the tran- sient response and steady state of the reference model, so that the desired reference signal can perform as a guide- line for the tracking control system, for example, if the real parts of eigenvalues of r are more negative, the tracking control system follow a traj ectory prescribed by rt sooner. In Europe, consider the historical data gem 1 starting at 1960, it is reasonable to assume an average growth rate of GDP around 3.5%, and the present growth rate of GDP is around 4% for Europe. Moreover, the chan in total forest cover fro990 to 2000 was posi- tive due to reforestation, but corresponding to only 0.3% Copyright © 2011 SciRes. JEP  Robust Resource Management Control for CO2 Emission and Reduction of Greenhouse Effect: Stochastic Game Approach Copyright © 2011 SciRes. JEP 1182 Figure 2. Simulation and comparison between model and actual data. To fit the actual data, the invariant control efforts: reforestation u1, clean technology u2 and CO2 tax u3, are assumed to be 0.012%, 0.08% and 0 respectively [3]. Figure 3. The CO2 emission system with invariant control efforts under stochastic disturbance. It is seen that the control abil- ity would not be guaranteed under parametric fluctuations and environmental noises.  Robust Resource Management Control for CO Emission and Reduction of Greenhouse Effect: 1183 2 Stochastic Game Approach per year [3]. Thus, for the purpose of robust resource ma- nagement control for CO2 emission and reduction of greenhouse effect, the reference model is set via and the initial state value in 2010 as 10 0 0 0.10 00 0.1 r A , 398 ( )19.31 3514.14 rt 00 r x of clean techno to si- mulate the desired progressive pro cess lo- gy improvement, forest expansion and GDP increase after 2010. Therefore, based on the reference model, the CO2 concentration could be decreased to the value in 1960, and GDP could reach a desired steady state that is pre- scribed without limiting the growth of GDP (Figure 4), i.e. the GDP growth can not be less than the original GDP growth rate 4% in Europe. And the expansion rate of forested area can also be higher than 0.3% until reach an appropriate value. To avoid solving th e HJI in Theorem 1, the T-S fuzzy model is employed to approximate the nonlinear stochas- tic system described in above section. For the conve- nience of control design, each state is taken with 3 op- eration points respectiv ely, and triangle type me mbership functions are taken for the 27 Rules (Figure 5). In order to accomplish the robust minimax tracking performance of the desired reference signal, in spite of the worst in- fluence of stochastic parametric fluctuation, environ- mental noise, and minimize the control efforts, a set of weighting matrices and are tuned up as follows QR 4 4 4 10 0 0 0 10 0 0 0 10 Q ; 4 4 4 10 0 0 0 10 0 0 0 10 R i.e. with a heavy penalty on the control effort and a light penalty on the tracking error in (8). After that the LMI-constraind op timization problem in (32) and (33) for the robust minimax tracking control can be solved by using Matlab Robust Control Toolbox. Fi- nally, a minimum 01.39 and the associated com- mon positive definatrixcan be ob- tained as follows ite symmetric m P 0.0009 0.0007 0.0000 0.0009 0.0007 0.0000 0.0007 0.0015 0.0000 0.0007 0.0015 0.00 00 1 15 0.0000 0.0000 0.0000 0.0161 0.0000 0.0000 0.016 0.0009 0.0007 0.0000 P 0.0007 0.00 0.0000 0.0000 0.0161 0.0022 0.0010 0.0000 0.0010 0.0030 0.0000 0.0000 0.0000 0.0252 Thus the robust minimax tracking control is designed atrix, according to these imperative parameters and mi.e. 27 1 1 T jj j ut hztRBPxt to track the desired refer- ence signal to the end (Figure 6). In Figure 7, it shows the responses of the controlled CO2 emission system with the robust minimax tracking control. As the CO2 emission target is approached, both investments in refor- estation and clean technology tend to decrease, and a positive carbon tax revenue co uld be ach ieved in the end. From the simulation results, it is seen that the effect of intrinsic parametric fluctuations and external distur- ba erformance of the robust minimax tracking control via T–S fuzzy interpolation is quite satisfactory. 5. Discussion From the computer simulation, it is shown that the CO2 f6 rm disturbances (Figure 3). To achieve actual demands, i.e. the system can track an appropriate reference model as soon as possible without limiting GDP growth, forest area increase and guarantee CO2 emission decrease under nces on the reference model tracking of CO2 emission system can be overcome efficiently by the proposed ro- bust minimax tracking control design. Thus, the tracking p emission system with invariant control efforts can fit the actual data perfectlyrom 190 to 2010, but could not guarantee its perfoance under intrinsic or external disturbances or modeling errors, the robust model refer- ence tracking control is proposed from a dynamic game theory perspective, and then can be efficiently solved by fuzzy stochastic game approach. By employing the robust minimax tracking controls ut (Figure 6) instead of using the invariant controls from 2010 to 2030, the robust minimax tracking per- formance is guaranteed under an upper bound 0 , no matter what stochastic property of noise what of the uncertain initial condition vt and value 0 . With the led period (2010~2030) (Figure e n- and companies following the robuma track- ntrol in gover x control ment ing co 7), th minist ut ut limi can reduce CO2 emi a red withoting forest area ang by ssion to d GDP increasi desi nvalue Copyright © 2011 SciRes. JEP 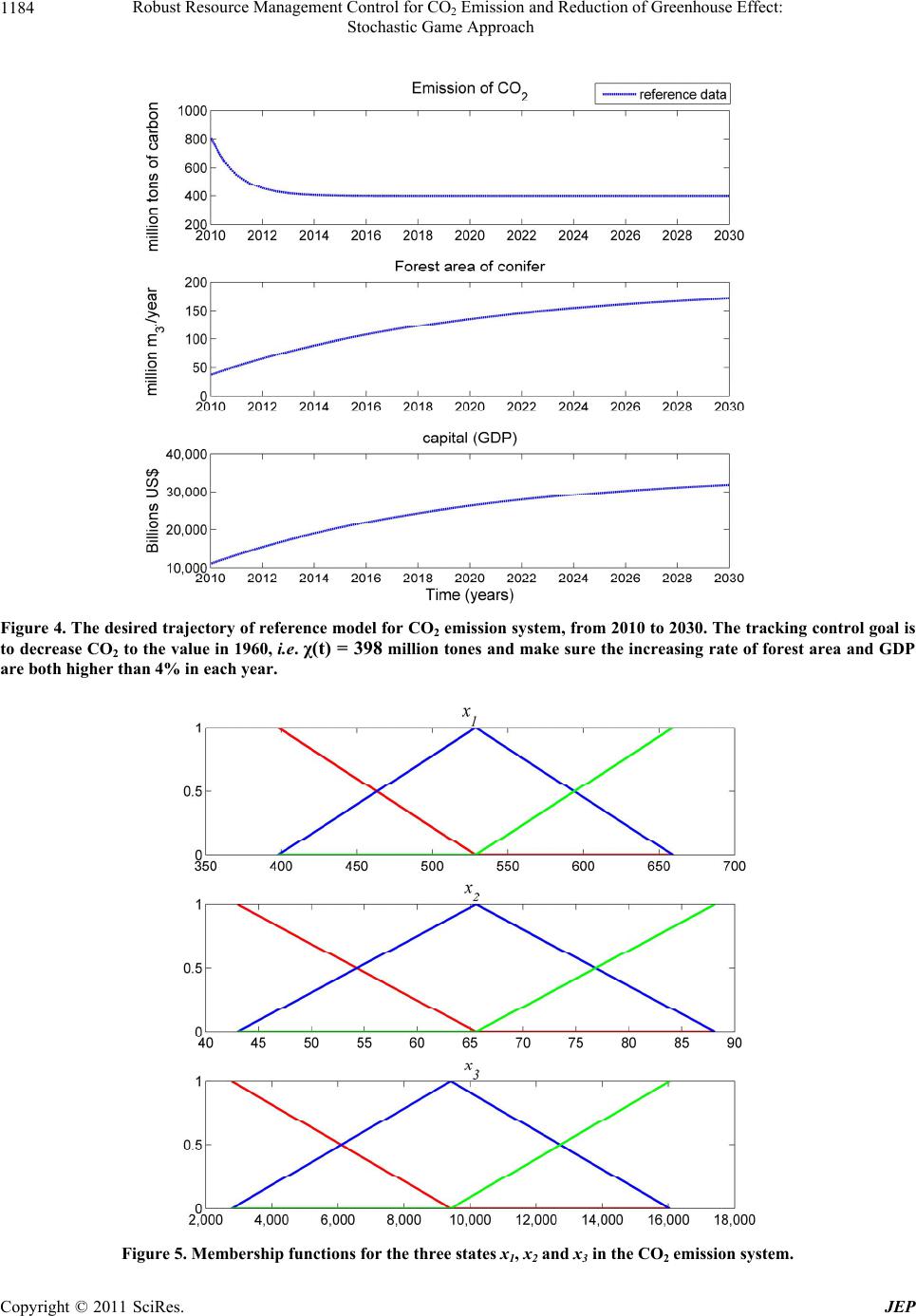 Robust Resource Management Control for CO Emission and Reduction of Greenhouse Effect: 1184 2 Stochastic Game Approach sion system, from 2010 to 2030. The tracking control goal is s and make sure the increasing rate of forest area and GDP Figure 4. The desired trajectory of reference model for CO2 e to decrease CO2 to the value in 1960, i.e. χ(t) = 398 million t are both higher than 4% in each year. mis one Figure 5. Membership functions for the three states x1, x2 and x3 in the CO2 emission system. C opyright © 2011 SciRes. JEP  Robust Resource Management Control for CO Emission and Reduction of Greenhouse Effect: 1185 2 Stochastic Game Approach Figure 6. The robust minimax tracking control in the simulation example. Figure 7. The trnimax tracking control, under the acking performance of CO2 emission system to a desired reference model by the robust mi influence of parametric fluctuations and environmental noises. Copyright © 2011 SciRes. JEP  Robust Resource Management Control for CO2 Emission and Reduction of Greenhouse Effect: Stochastic Game Approach Copyright © 2011 SciRes. JEP 1186 managing expenditure in clean technology 2 ut, refor- estation 1 ut and CO2 revenue 3 ut. efforts From 6, the controlofrestation Figure refo 1 ut technology , and investment in innovating or improving clean 2 ut y poi forestat on dy ive of comp ributio cause se effect un , in simulation increase acutely during rly stage and then converge to the stable values, h clearlnts out the urgent need of a concerted of reion and clean technology to change the emissinamics into a desired trajectory. From rspectdesired economic development, at the ng,anies produced more pollutions (which means they emit more CO2) may also have more eco- ic contns to GDP growth [36] and then GDP deteriorates beof the cost of global warming and outil a balance. The control effort of venue the ea whic effort CO2 the pe beginni nom greenh CO2 re 3 ut reasonab in our simulation also interprets this nly by an acute descent to negative and then climb to positive gently, which means to ensure the unlimited GDP growth and following a desired reference model, the government should provide a financial sub- sidy to improve indu strial th rough pu t in ear ly years, even it creates more pollution, until the scale enterprises can bear the loss of carbon tax. By tuning the weighting matrices of error punishment and control cost , m en account, becau invariant when tobust minimax tracking control starts. In this studyshown that the tracking error is nished by a low and a high control cost, which means to guarantee the robust minimax tracking control performance, the control strategy can endure more tracking error by using less control, thus making the control method efficiently and viably. If the CO emission model is free of external distur- bance, i.e. , the robust tracking control performance has a loweptimal upper bound situatio Q k e pu R se t he r , it is Q ore situation in reality can be he cost of control inputs may not ta b R 20c r subo00.41 ore . It implies that if theurements of states are maccurate, and the controlled system could track the desired reference trajectory more sophistically, which means the control design for t he C O2 emission system is more precisely. Although international cooperation from tradable quotas and permits can reduce CO2 emission efficiently, uncertainties about compliance costs have caused coun- tries to withdraw from negotiations. Without tuning any system parameters, these time-invariant control efforts could make the CO2 emission system too rigid to respond for an immediate need or lead the CO2 emission system toward an uncontrollable circumstance under disturbance, which may finally lose its control ability for actual dy- namics of CO2 emission system. Optimal control method guarantee the control performance. If the more flexible CO2 emission targets can be made to incorporate opti- mum choices of investments with minimum impact on the GDP growth, i.e. taking account of the stochastic disturbances with respect to minimax tracking control problem, then climate agreements for reducing green- house effect may become more attractive and efficient [25,37]. In this study, the fuzzy interpolation technique is em- ployed to approximate the nonlinear CO2 emission sys- tem, so that LMIs technique is used to efficiently solve the nonlinear minimax optimization problem in our ro- bust minimax tracking design procedure. Since the pro- posed robust minimax tracking control design can efficiently control the CO2 emission in real time to pro- tect environment from the global warming and reduce greenhouse effect, in the future, the applications of ro- bust minimax tracking control design for environmental resource conservation and pollution control under sto- chastic disturbance would be potential in ecological and economic field. 6. Conclusions If current GHG concentrations remainstant, the eral centuries of in- res and sea level rise. Slowing such climate change requires overcoming inertia in political, technological, and geophysical systems. To efficiently manage the resources commitment for de- creasing the atmospheric CO2, mathematical methods have been proposed to help people make decision. How- ever, how to ensure the desired CO2 emission perform- ance under stochastic disturbances is still important and infancy. In this study, based on robust control theory and dynamic game theory, a nonlinear stochastic game prob- lem is equivalent to a nonlinear robust minimax tracking problem, for controlling the CO2 emission system to achieve a desired time response under the influence of parametric fluctuations, environmental noises and un- known initial conditio ns. To solve the nonlinear HJI-constrained problem for the robust minimax tracking control design is generally difficult. Instead of solving the HJI-constrained problem, a fuzzy stochastic game approach is proposed to trans- form this nonlinear robust minimax tracking control problem into a set of equivalent linear robust minimax problems. Such transformation allows us to solve an equivalent LMI-constrained problem for this robust minimax tracking control design in an easier way with the help of Robust Control Toolbox i Matlab. etric fluctuation and environmental noise meas n co world would be committed to sev creasing global mean temperatu without take account of the effect of intrinsic and exter- nal disturbances in the design procedure could even not This robust minimax tracking method not only con- siders the param n  Robust Resource Management Control for CO Emission and Reduction of Greenhouse Effect: 1187 2 Stochastic Game Approach in a ditio initial condition of the sy meth und and 7-001-ASP. but also guarantees the tracking performance subop- timal conn. And the unknown stem also be considered as a random factor, thus this od can be used to control the CO2 emission system tracking aroany feasible reference model whenever the control of this system starts. Although this theoretical method rests on the con s erva tive su bop ti mal method , this fact doesn’t frustrate its potential as a government policy guideline and the power of prediction in public d ecision- making. Once these obstacles have been surmounted, i.e. more rapid response by real time monitor via e-govern- ment implementation, this method would be powerful to control and manage the economic and ecological re- source. What is more is that for its convenient and effi- cient control design for nonlinear systems with paramet- ric fluctuationstochastic uncertainties, this dynamic game approach can be applied in other fields with similar demands. 7. Acknowledgements The work was supported by the National Science Coun- cil of Taiwan under grant No. NSC 99-2745-E-007-001- ASP and NSC 100-2745-E-00 REFERENCES [1] T. M. L. Wigley, “The Climate Change Commitment,” Science, Vol. 307, No. 5716, 2005, pp. 1766-1769. doi:10.1126/science.1103934 [2] P. Friedlingstein anS. Solomon, “Contributions of Past and Present Human Generations to Committed Warming Caused by Carbon Dioxide,” Proceedings of the National Academy of Sciences of the United States of America, Vol. 102, No. 31, 2005, pp. 10832-10836. d doi:10.1073/pnas.0504755102 [3] M. A. L.etano, D. F. M. Gherardi and T. Yoneyama, “Optimal Resource Management Control for CO2 Emis- sion and Reduction of the Greenhouse Effect,” Ecologi- cal Modelling, Vol. 213, No. 1, 2008, pp. 119-126. Ca doi:10.1016/j.ecolmodel.2007.11.014 [4] S. J. Davis, K. Caldeira and H. D. Matthews, “Future CO2 Emissions and Climate Change from Existing Energy In- frastructure,” Science, Vol. 329, No. 5997, 2010, pp. 1330-1333. doi:10.1126/science.1188566 [5] A. Salehi-Khojin, K. Y. Lin, C. R. Field, et al., “Nonther- mal Current-Stimulated Desorption of Gases from Car- bon Nanotubes,” Science, Vol. 329, No. 5997, 2010, pp. 1327-1330. doi:10.1126/science.1194210 [6] J. D. Scheraga and N. A. Leary, “Improving the Effi- ciency of Policies to Reduce CO2 Emissions,” Energy Policy, Vol. 20, No. 5, 1992, pp. 394-404. doi:10.1016/0301-4215(92)90061-6 [7] UNEP, “United Nations Environment Program,” http://www.unep.org/ [8] G. Marland, T. A. Boden, R. J. Andres, et al., “Global, Regional, and National Fossil Fuel CO2 Emissions,” Carbon Dioxide Information Analysis Center, Environ- mental Sciences Division, Oak Ridge National Labora- tory, Oak Ridge, 2006. [9] WWF, “World Wildlife Fund,” http://www.wwf.org.uk/researcher/issues/footprint/index. asp. [10] UNFCCC, “United Nations Framework Convention on Climate Change, Status of Ratification of the Kyoto Pro- tocol,” http://unfccc.int/kyoto_protocol/status_of_ratification/ite ms/2613.php. [11] W. D. Nordhaus, “To Slow or Not to Slow: The Eco- nomics of the Greenhouse Effect,” The Economic Journal, Vol. 101, No. 407, 1991, pp. 920-937. doi:10.2307/2233864 [12] W. D. Nordhaus, “A Sketch of the Economics of the Greenhouse Effect,” The American Economic Review, Vol. 81, No. 2, 1991, pp. 146-150. [13] W. D. Nordhaus, “Reflections on the Economics of Cli- mate Change,” The Journal of Economic Perspectives, Vol. 7, No. 4, 1993, pp. 11-25. [14] J. M. Poterba, “Global Warming Policy: A Public Fi- ve,” The Journal of Economic Perspec- 63. nance Perspecti tives, Vol. 7, No. 4, 1993, pp. 47- [15] K. R. Stollery, “Constant Utility Paths and Irreversible Global Warming,” Canadian Journal of Economics, Vol. 31, No. 3, 1998, pp. 730-742. doi:10.2307/136210 [16] M. A. L. Caetano, D. F. M. Gherardi, G. P. Ribeiro, et al., “Reduction of CO2 Emission by Optimally Tracking a Pre-Defined Target,” Ecological Modelling, Vol. 220, No. 19, 2009, pp. 2536-2542. doi:10.1016/j.ecolmodel.2009.06.003 [17] B. K. Oksendal, “Stochastic Differential Equations: An Introduction with Applications,” Springer Verlag, New York, 2003. [18] B. S. Chen, C. S. Tseng and H. J. Uang, “Robustness Design of Nonlinear Dynamic Systems via Fuzzy Linear Control,” IEEE Transactions on Fuzzy Systems, Vol. 7, No. 5, 2002, pp. 571-585. doi:10.1109/91.797980 [19] B. S. Chen, C. S. Tseng and H. J. Uang, “Mixed H2/H∞ Fuzzy Output Feedback Control Design for Nonlinear Dynamic Systems: An LMI Approach,” IEEE Transac- tions on Fuzzy Systems, Vol. 8, No. 3, 2002, pp. 249-265. doi:10.1109/91.855915 [20] T. Takagi and M. Sugeno, “Fuzzy Identification of Sys- tems and Its Applications to Modeling and Control,” IEEE Transactions on Systems, Man, and Cybernetics, Vol. 15, 1985, pp. 116-132. [21] W. H. Zhang and B. S. Chen, “State Feedback H∞ Con- trol for a Class of Nonlinear Stochastic Systems,” SIAM. Journal on Control and Optimization, Vol. 44, 2006, pp. 1973-1991. doi:10.1137/S0363012903423727 [22] W. H. Zhang, B. S. Chen and C. S. Tseng, “Robust H∞ Copyright © 2011 SciRes. JEP  Robust Resource Management Control for CO2 Emission and Reduction of Greenhouse Effect: Stochastic Game Approach Copyright © 2011 SciRes. JEP 1188 Filtering for Nonlinear Stochastic Systems,” IEEE Trans- actions on Signal Processing, Vol. 53, No. 2, 2005, pp. 589-598. doi:10.1109/TSP.2004.840724 [23] P. Agostini, M. Botteon and C. Carraro, “A Carbon Tax to Reduce CO2 Emissions in Europe,” Energy economics, Vol. 14, No. 4, 1992, pp. 279-290. doi:10.1016/0140-9883(92)90034-B [24] R. Boyd, K. Krutilla and W. K. Viscusi, “Energy Taxa- tion as a Policy Instrument to Reduce CO2 Emissions: A Net Benefit Analysis,” Journal of Environmental Eco- nomics and Management, Vol. 29, No. 1, 1995, pp. 1-24. doi:10.1006/jeem.1995.1028 [25] R. McKitrick, “What’s Wrong with Regulating Carbon Dioxide Emissions,” A Briefing at the United States Con- gress, 2001. [26] F. B. Hanson, “Applied Stochastic Processes and Control for Jump-Diffusions: Modeling, Analysis, and Computa- tion,” Society for Industrial and Applied Mathematics, Philadelphia, 2007. doi:10.1137/1.9780898718638 [27] S. Boyd, L. El Ghaoui, E. Feron, et al., “Linear Matrix Control Theory,” Society for thematics, Philadelphia, 1994 H2/H∞ Con- trol with StateE Transactions on Automatic Con4, pp. 45-57. Inequalities in System and Industrial and Applied Ma . [28] T. Basar and G. J. Olsder, “Dynamic Noncooperative Game Theory,” Society for Industrial and Applied Mathematics, 2nd Edition, Philadelphia, 1999. [29] B. S. Chen and W. H. Zhang, “Stochastic -Dependent Noise,” IEE trol, Vol. 49, No. 1, 200 doi:10.1109/TAC.2003.821400 [30] K. Tanaka and H. O. Wang, “Fuzzy Control Systems rate Document Repository, Euro- tudy 1960-2000-2020— /www.fao.org/docrep/008/ae428e/ae428e00.htm atistics.htm h Service,” bal Environment, ental Assessment Agency,” inters, Eds., The Eco- Optimal Intensity Targets Design and Analysis: A Linear Matrix Inequality Ap- proach,” Wiley-Interscience, New York, 2001. [31] WRI, “World Resources Institute, Earth Trends Envi- ronmental Information,” http://www.earthtrends.wri.org. [32] FAOSTAT, “Fao Corpo pean Forest Sector Outlook S Main Report,” http:/ [33] A. Maddison,” The World Economy,” http://www.theworldeconomy.org/publications/worldeco nomy/st [34] USDA, “United States Department of Agriculture, Eco- nomic Researc http://www.ers.usda.gov/Data/macroeconomics/Data/Hist oricalGDPDeflatorValues.xls [35] HYDE, “History Database of the Glo Netherlands Environm http://www.rivm.nl/hyde/bdf/gdp. [36] G. M. Grossman, “Pollution and Growth: What Do We Know?” In: I. Goldin and L. A. W nomics of Sustainable Development, Cambridge Univer- sity Press, Cambridge, 1995, pp. 19-50. [37] F. Jotzo and J. C. V. Pezzey, “ for Greenhouse Gas Emissions Trading under Uncer- tainty,” Environmental and Resource Economics, Vol. 38, No. 2, 2007, pp. 259-284. doi:10.1007/s10640-006-9078-z  Robust Resource Management Control for CO Emission and Reduction of Greenhouse Effect: 1189 2 Stochastic Game Approach 14), let us Appendix A: Proof of Theorem 1 Equation Section (Next) For the augmented stochastic system in (de- note a Lyapunov energy function 0Vxt for 00x with 00.V Then the regulation problem in (15) is equivalent to the following minimax problem 2, 0 tTT T dVx t 0 0 )f f minmax,minmax ( ut ut vt vt ut vtEVx V xtdt xtQxtutRutvtvtdtx (A1) By Ito formula in Lemma 1 [21,22], we get 2 d1 d2 T xt Vxt wt 2 dd1 d T T Vxt VxtVx xt Hxt tx 2 tHxt 2 d 2tt T Vx t xtGxt ut CvtHxtH xtHxt t (A2) xt xt Substituting (A2) to (A1) and by the fact that d d wt Et0 , we get () () minmax , minmax 0 ut vtJut vt EVx Vxt () () 0 2 1 TT T xtQxtu tRutvtvt Vxt Vxt Cv t 2d, 0 2 minmax (0) () () T Hx tHx ttx xt xt EVx V ut vt () () T TVx t Vxt Fxt Gxtut xt xt 2 f f ut vt tT 12 0 2 11 2 () 11 44 111 222 1 2 f f TT T tTT T T TTT T xt VxtVxtVxt Vxt Vxt FxtxtQxtGxtRGxtCC txtxtxtxt VxtVxt Vxt HxtHxtutRGxtRutRGxt xt xt xt V vtC 1d,0 2 T T xtV xt vtCt x xt xt Then the minimax solution is given as follows ** 1 0 2 22 ,0 1 4 11 0 2 4 f f TT tTT T TT Ju tvtEVxVxt VxtVxt Vxt FxtxtQxtGxtR Gxt txt Vxt VxtVxt CCHx tHx tx xt xtxt , xt Copyright © 2011 SciRes. JEP  Robust Resource Management Control for CO Emission and Reduction of Greenhouse Effect: 1190 2 Stochastic Game Approach with 1 1() T ut RG 2 () , 1 2 T Vxt xt 2 t. Vx t vtC xt If Equation (1 9 ) hol ds, t hen ,0 f utvt EVxVxt . From the inequality in (16), the minimax solution should be less than 200 T Ex Ix . After that the inequality in (20) is obtainws ed as follo 2 00 0,0 T EV xExIxx . Q.E.D. Appendis B: Proof of Theorem 2 Equation Section (Next) For the fuzzy system in (27), let us denote a Lyapunov function ,0 f Jut vtEVxVxt 0 T Vxtx tPxt , for 00x with 00.V is equivaThen the minimax regulation problem lent to the following in (16) 2 0 d mid ,0 d f t TTTT T ff Vxt nmax,minmax0 0 ut ut vt vt u tvtExPxxxt Q tPx tx tut Rutvt vttx t (B1) By Ito formula in Lemma 1 [21,22], we get 111 d2 d LLL TTT iiiiijij iij Vxt dw t tPh ztAxtButCvtDh zthztxtDPDxt tdt (B2) Substituting (B2) to (B1) and by the fact that d0 d wt Et , we get 2 01 11 2 1 minmax00 2 d minmax0 0 1 f TT ff ut vt L tTT TT iii i LL TT ij ij ij TT ff ut vt L TTTTTT ii i E xPxxtPx t xtQxtutRutvtvtxtP hztAxt ButCvt hzth zt xtDPDxtt ExPxx tPxt xtQxthzt xtPAxt xtAPxtxtPCC i 0 1 11 11 1 11 11 d minmax0 0 f t LL LL TT TT ijijij ij ij ij T T LL TTT iij j ii TT f ut vt Px t h zthztxtPBRBPxthzthztxtDPDxt RuthztBPx tRRuthztBPx tvtCPx tvtCPx tt ExPxx tP T 1 2 011 1 11 1 11 () d f f LL tTTT TT ijii ijij ij T T LL TTT ii ii ii xt hzthztxtPAAPQPB RBPPCCPDPDxt RuthztBPx tRRu thztBPx tv tCPxtvtCPx tt T C opyright © 2011 SciRes. JEP  Robust Resource Management Control for CO Emission and Reduction of Greenhouse Effect: 1191 2 Stochastic Game Approach inimax solution is given as follows The m 1 2 011 ,00 1d f TT ff LL tTTT TT ijii ijij ij JutvtE xPxxtPxt hzth zt xtPAAPQ PBR BPPCCPDPDxtt with 1 1 LT jj j ut hztRBPxt , 2 1T vt CPxt . In order to simplify the above equation, suppose the inequality in (29) hold, then 2 00 ut vt ff TT minmax ,, 00 00 TT ut vtJutvt ExPxxt x Ix i.e. Pxt Ex PxE 2 PI . Q.E.D. Copyright © 2011 SciRes. JEP
|