Journal of Signal and Information Processing, 2011, 2, 322-329
doi:10.4236/jsip.2011.24046 Published Online November 2011 (http://www.SciRP.org/journal/jsip)
1
A Wavelet Spectrum Technique for Machinery
Fault Diagnosis
Derek Kanneg1, Wilson Wang2
1eMech Systems Inc., Thunder Bay, Canada; 2Department of Mechanical Engineering, Lakehead University, Thunder Bay, Canada.
Received June 13th, 2011; revised August 3rd, 2011; accepted August 12th, 2011.
ABSTRACT
Rotary machines are widely used in various applications. A reliable machinery fault detection technique is critically
needed in industries to prevent the machinery system’s performance degradation, malfunction, or even catastrophic
failures. The cha llenge for reliable fault diagnosis is related to the ana lysis of non-stationary features. In this paper, a
wavelet spectrum (WS) technique is proposed to tackle the challenge of feature extraction from these non-stationary
signatures; this work will focus on fault detection in rolling element bearings. The vibration signatures are first ana-
lyzed by a wavelet transform to demodulate representative features; the periodic features are then enhanced by
cross-correlating the resulting wavelet coefficient functions over several contributive neighboring wavelet bands. The
effectiveness of the proposed techn ique is examined by experimen tal tests correspond ing to differen t bearing cond itio ns.
Test results show that the developed WS technique is an effective signal processing approach for non-stationary feature
extraction and analysis, and it can be applied effectively for bearing fault detection.
Keywords: Machinery Condition Monitoring, Rotary Machines, Bearing Fault Detection, Non-Stationary Signal,
Wavelet Transform, Resonance Feature
1. Introduction
Rolling element bearings are widely used in rotary ma-
chinery. A reliable bearing fault diagnostic technique is
critically needed in a wide array of industries to prevent
machinery performance degradation, malfunction, or ev-
en catastrophic failures [1]. Bearing condition monitoring
usually involves two sequential processes: feature extrac-
tion and fault diagnosis [2]. Feature extraction is a proc-
ess in which health condition related features are extra-
cted by appropriate signal processing techniques, wher-
eas fault diagnosis is a decision-making process to esti-
mate bearing health conditions based on the extracted
representative features. Therefore, feature extraction pla-
ys the key role for bearing health condition monitoring,
whereas non-robust features may lead to false alarms (i.e.,
an alarm is triggered by some noise instead of a real
bearing fault) or missed alarms (i.e., the monitoring tool
cannot recognize the existence of a bearing defect) in
diagnostic operations [3].
Several techniques have been proposed in the literature
for bearing fault-related feature extraction, in which the
analysis can be performed in the time domain, the frequ-
ency domain, or the time-frequency domain [4-6]. In
time-domain analysis, for example, a bearing fault is det-
ected by monitoring the variation of some statistical in-
dices such as root-mean-square value, crest factor or ku-
rtosis. A bearing is believed to be damaged if the mon-
itoring indices exceed predetermined thresholds; howev-
er, it is usually challenging to determine robust threshol-
ds in real-world applications. Frequency-domain analysis
is based on the transformed signal in the frequency do-
main. The advantage of frequency-domain analysis over
time-domain analysis is its capability to easily identify
and isolate certain spectral components of interest [7].
Bearing health conditions are assessed by examining the
fault related characteristic frequency components in a
spectrum or in some extended spectral expressions such
as bispectrum or cepstrum maps [8,9]. Frequency-based
techniques are usually supplemented with certain signal
analysis methods to enhance representative spectral com-
ponents, which include frequency filters, envelope analy-
sis, and modulation sidebands analysis [10]. Frequency-
domain techniques, however, are not suitable for the an-
alysis of non-stationary signatures that are generally rela-
ted to machinery defects. Non-stationary or transient sig-
natures can be analyzed by applying time-frequency do-

A Wavelet Spectrum Technique for Machinery Fault Diagnosis323
main techniques such as the short-time Fourier transform
(FT) [11], Wigner-Ville distribution [12], spectral kurto-
sis [13], cyclostationary analysis [14], or wavelet trans-
form (WT) [15]. In bearing fault diagnosis, the WT is a
favorite technique, because it does not contain such cross
terms as those in the Wigner-Ville transform, while it can
provide a more flexible multi-resolution solution than the
short-time FT. According to signal decomposition para-
digms, the WT can be classified as the continuous WT,
discrete WT, wavelet packet analysis, and those WT with
post-processing schemes [16-19].
If a bearing is damaged, the generated vibration sig-
natures could be either stationary or non-stationary. It is
relatively easier to analyze the stationary signatures using
some classical fault detection techniques [20]. However,
it still remains a challenging task to extract robust repre-
sentative features from the non-stationary vibration sig-
nals (e.g., those generated from a fault on bearing rotat-
ing components), particularly in real-world industrial ap-
plications. This is because: 1) a bearing is a system in-
stead of a simple mechanical component, which consists
of inner/outer rings as well as a number of rolling elem-
ents; 2) slippage often occurs between the rolling elem-
ents and rings in operations; and 3) the machinery opera-
tion conditions are usually noisy. Correspondingly, the
objective of this paper is to develop a wavelet spectrum
(WS) technique to tackle this challenge in which the rep-
resentative periodic features will be enhanced by an inte-
gration process over several contributive wavelet bands.
2. The Wavelet Spectrum (WS) Technique
Whenever a fault occurs on a bearing component, impa-
cts are generated in operation, which in turn excite the
bearing and its support structures. The resulting resona-
nce signatures are usually amplitude modulated by the
bearing defect [2]; therefore, the analysis of these reso-
nance signatures plays a key role in vibration-based
bearing fault detection. Figure 1(a) shows part of a typi-
cal acceleration signal, measured from the housing of a
tested bearing with an inner-race defect when the shaft
speed t
f
= 35 Hz. When a defect occurs on a bearing
rotating component, the modes and magnitudes of the
resulting resonances often vary over time due to the
variation in angular position of the impacts [20]; this
non-stationary characteristic of condition-related signa-
tures makes bearing fault detection still remain a very
challenging task in both research and industrial applica-
tions. In this work, a WS technique is proposed to invest-
tigate the characteristics of these non-stationary reson-
ance signatures for the purpose of bearing fault detection.
The WS technique involves five steps for signal process-
ing, as discussed as follows.
The first step is to apply the WT to demodulate the
resonance vibration signatures, both stationary and non-
stationary, over a series of wavelet bands. Given a cont-
inuous signal


x
t, the wavelet coefficients are deter-
mined by
  
*
,dWtsxsw st






 
(1)
Where


*
wt denotes the complex conjugation of mo-
ther wavelet function


wt ; s and t are the scale and
time variables, respectively, which produce dilation and
translation [20]. The choice of an appropriate mother
wavelet depends on the signal properties and the purpose
of the analysis. By testing and comparison, Morlet
wavelet is selected as the mother wavelet for the signal
analysis in this work, which is a modulated Gaussian
function:
 
2
0
2
0
expexp 2π
2
t
wtj ft
b





(2)
where 0 is the spread of the Gaussian function and 0 b
f
is the center frequency of the pass-band of the mother
wavelet. As 00
increases, the duration of the wavelet
expands, and the time resolution will decrease corre-
spondingly. As a result, the obtained mother wavelet
bf


wt may not be suitable to analyze fast-decaying tran-
sient signatures. To solve this problem, the product of the
spread and the scaled center frequency is kept as a con-
stant in this work, i.e.,

0
000
1
2ln2
ii i
i
b
bffs bf
s
 (3)
where 00 2π2ln2bf  was given in [20]; i
s
represents the ith selected scale; i
b and i
f
are the
corresponding ith spread and center frequency, respec-
tively. Based on the relation between i and i
b
f
as in
Equation (3), the mean of the obtained mother wavelet


wt will be kept less than 10–12 in this case, and the
effective support will vary with the scaled center frequ-
ency to accommodate the variation of the signatures of
interest. At each wavelet scale i
s
, the magnitude of
wavelet coefficient function

,i sWt that represents
the demodulated envelope signal is normalized by its
standard deviation, that is
 
  
2
11
,
,
1
,,
i
iLL
li li
ll
Wts
Wts
WtsWtsL
L



1





(4)
where l = 1,2, ···, L, and L is the total number of samples;
i = 1,2, ···, I, and I is the number of wavelet scales;


,
li
Wts is the lth sample of

,i Wts . To reduce the

A Wavelet Spectrum Technique for Machinery Fault Diagnosis 324
interference effects from the low-frequency noisy com-
ponents, in this work, the overall frequency band of in-
terest is chosen as


,2.56
ts
Zf f, where t
f
denotes the
shaft rotation speed, Z is the order of shaft harmonics,
t
Z
f represents the lower bound frequency for feature
extraction (Z = 35 is used in this case);
s
f
is the sam-
pling frequency, and the constant 2.56 is selected to
avoid aliasing effects. The centre frequencies of the
wavelet should be deployed properly to implement the
WT over this designated frequency band


,2.56f
ts ,
without the overlapping between the wavelet frequency
bands. Based on the FT of the dilated wavelet
Zf


wst,
the 3-dB bandwidth i for the ith centre frequency BW
i
f
is derived as follows:


1,BW f1
ii

  , where
ln 22π   is a constant. Beginning with the lower
bound frequency t, the centre frequencies Nf i
f
can be
recursively calculated and positioned as:


1i
i
1
1
it
f
Zf




, i = 1,2, ···, I – 1 (5)


11 i
f
1
22 .
s
i
f
f
56




 


I
, i = I (6)
where I is the number of the wavelet scales (7

in
this case). Figures 1(b)-(h) show the respective normal-
ized wavelet coefficients


,i Wts over seven wavelet
bands, which are determined based on the vibration sig-
nal as shown in Figure 1(a). It can be seen that the reso-
nance signatures in Figure 1(a) are usually demonstrated
in several consecutive wavelet bands (Figures 1(b)-(h))
due to the variation of the transient modes.
The second step to implement the proposed WS tech-
nique is to cross-correlate the wavelet coefficients from
the neighboring wavelet bands to enhance the de-
fect-related periodic features, that is,
 
,
*
1
,Xl EWtls



ii
Wtsi


(7)
 
i
i
Xl i
i
Xl


 (8)

where


E denotes the expectation function;


i
X
l
are the cross-correlation sequences that are normalized
by their standard deviation i

around the mean i

. In
estimating the correlation sequence, the method adopted
here is slightly different from the commonly used Pear-
son’s approach. Pearson product-moment correlation est-
imation limits

i
-0.4
0
0.4 (a)
Vib (V)
0
10 (b:i = 1)
0
10 (c:i = 2)
0
10 (d:i = 3)
0
10 (e:i = 4)
Wavelet coefficients
0
10
(f:i = 5)
0
10
(g:i = 6)
5001000 1500 2000 25003000
0
10
Sample points
(h:i = 7)
Figure 1. (a) Part of an acceleration signal generated by a
bearing with an inner-race defect; (b)-(h) The normalized
wavelet coefficients obtained from the vibration signal over
seven wavele t bands ( i =1, 2, ···, 7).
marked by arrows. From a physical perspective, each
time as a bearing incipient fault encounters its mating
components, an impact is generated, which in turn in-
duces the resonance of the local structure. Corresponding
to each impulse, the resonant response usually occurs
over consecutive frequency bands in a random nature.
Figures 2(a)-(f) illustrate the


i
X
l array deter-
mined from six pairs of neighboring wavelet bands. It is
seen that some periodic features are prominent (e.g., in
Figures 2(b), (e), and (f)) whereas others are less pro-
nounced (e.g., in Figures 2(a), (c), and (d)). Corre-
spondingly, another key process in bearing incipient fault
detection is how to properly choose the more contrib-
utive wavelet bands to integrate cross-correlation coeffi-
cient functions to highlight the periodic features.
X
l to the range of [-1 1] whereas the
proposed one can prevent such a restriction. It is also
noted that the cross-correlations are performed on the
neighboring wavelet bands; this is because the demodu-
lated features from the resonance signatures are usually
reflected on the adjacent wavelet bands. An example is
illustrated in Figure 1 where the extracted features are
Each periodic feature with high amplitudes will mod-
ify the distribution of correlation sequence and cause the
distribution more skewed and/or tailed, which could be
detected by the Jarque-Bera (JB) statistic [21,22]. In this
work, the correlation coefficient from each pair of neigh-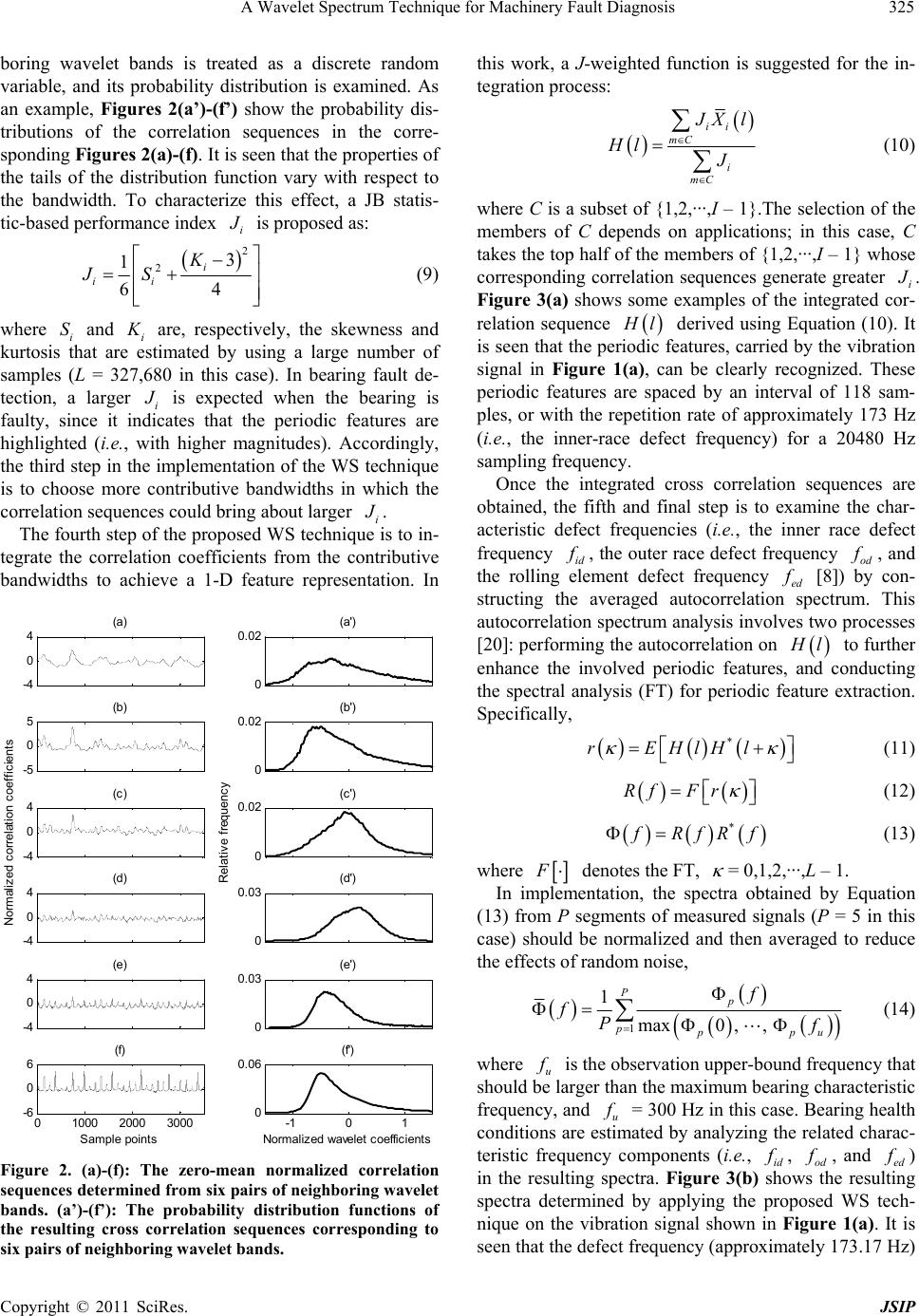

A Wavelet Spectrum Technique for Machinery Fault Diagnosis325
boring wavelet bands is treated as a discrete random
variable, and its probability distribution is examined. As
an example, Figures 2(a’)-(f’) show the probability dis-
tributions of the correlation sequences in the corre-
sponding Fig ures 2(a)-( f). It is seen that the properties of
the tails of the distribution function vary with respect to
the bandwidth. To characterize this effect, a JB statis-
tic-based performance index i
J
is proposed as:

2
23
1
64
i
ii
K
JS


 


 (9)
where i and i S
K
are, respectively, the skewness and
kurtosis that are estimated by using a large number of
samples (L = 327,680 in this case). In bearing fault de-
tection, a larger i
J
is expected when the bearing is
faulty, since it indicates that the periodic features are
highlighted (i.e., with higher magnitudes). Accordingly,
the third step in the implementation of the WS technique
is to choose more contributive bandwidths in which the
correlation sequences could bring about larger i
J
.
The fourth step of the proposed WS technique is to in-
tegrate the correlation coefficients from the contributive
bandwidths to achieve a 1-D feature representation. In
-4
0
4(a)
-5
0
5(b)
-4
0
4
Normalized c orrelati on c oeff i cient s
(c )
-4
0
4(d)
-4
0
4(e)
01000 2000 3000
-6
0
6
Sample points
(f)
0
0.02 (a')
0
0.02 (b')
0
0.02 (c')
Relat ive frequenc y
0
0.03 (d')
0
0.03 (e')
-1 0 1
0
0.06 (f')
Normal i zed wavelet coeffic i ents
Figure 2. (a)-(f): The zero-mean normalized correlation
sequences determined fr om six pairs of neighboring wavelet
bands. (a’)-(f’): The probability distribution functions of
the resulting cross correlation sequences corresponding to
six pairs of neighboring wavelet bands.
this work, a J-weighted function is suggested for the in-
tegration process:
 
ii
mC
i
mC
J
Xl
Hl J




 (10)
where C is a subset of {1,2,···,I – 1}.The selection of the
members of C depends on applications; in this case, C
takes the top half of the members of {1,2,···,I – 1} whose
corresponding correlation sequences generate greater i
J
.
Figure 3(a) shows some examples of the integrated cor-
relation sequence


H
l derived using Equation (10). It
is seen that the periodic features, carried by the vibration
signal in Figure 1(a), can be clearly recognized. These
periodic features are spaced by an interval of 118 sam-
ples, or with the repetition rate of approximately 173 Hz
(i.e., the inner-race defect frequency) for a 20480 Hz
sampling frequency.
Once the integrated cross correlation sequences are
obtained, the fifth and final step is to examine the char-
acteristic defect frequencies (i.e., the inner race defect
frequency id
f
, the outer race defect frequency od
f
, and
the rolling element defect frequency ed
f
[8]) by con-
structing the averaged autocorrelation spectrum. This
autocorrelation spectrum analysis involves two processes
[20]: performing the autocorrelation on

H
l to further
enhance the involved periodic features, and conducting
the spectral analysis (FT) for periodic feature extraction.
Specifically,



 
*
rEHlHl






 (11)


Rf Fr   



(12)




*
f
RfR f (13)
where


F

denotes the FT, = 0,1,2,···,L – 1. 
In implementation, the spectra obtained by Equation
(13) from P segments of measured signals (P = 5 in this
case) should be normalized and then averaged to reduce
the effects of random noise,
 



1
1
max0 ,,
Pp
ppp
f
fPu
f


 
 (14)
where u is the observation upper-bound frequency that
should be larger than the maximum bearing characteristic
frequency, and u = 300 Hz in this case. Bearing health
conditions are estimated by analyzing the related charac-
teristic frequency components (i.e., id , od , and ed)
in the resulting spectra. Figure 3(b) shows the resulting
spectra determined by applying the proposed WS tech-
nique on the vibration signal shown in Figure 1(a). It is
seen that the defect frequency (approximately 173.17 Hz)
f
f
f ff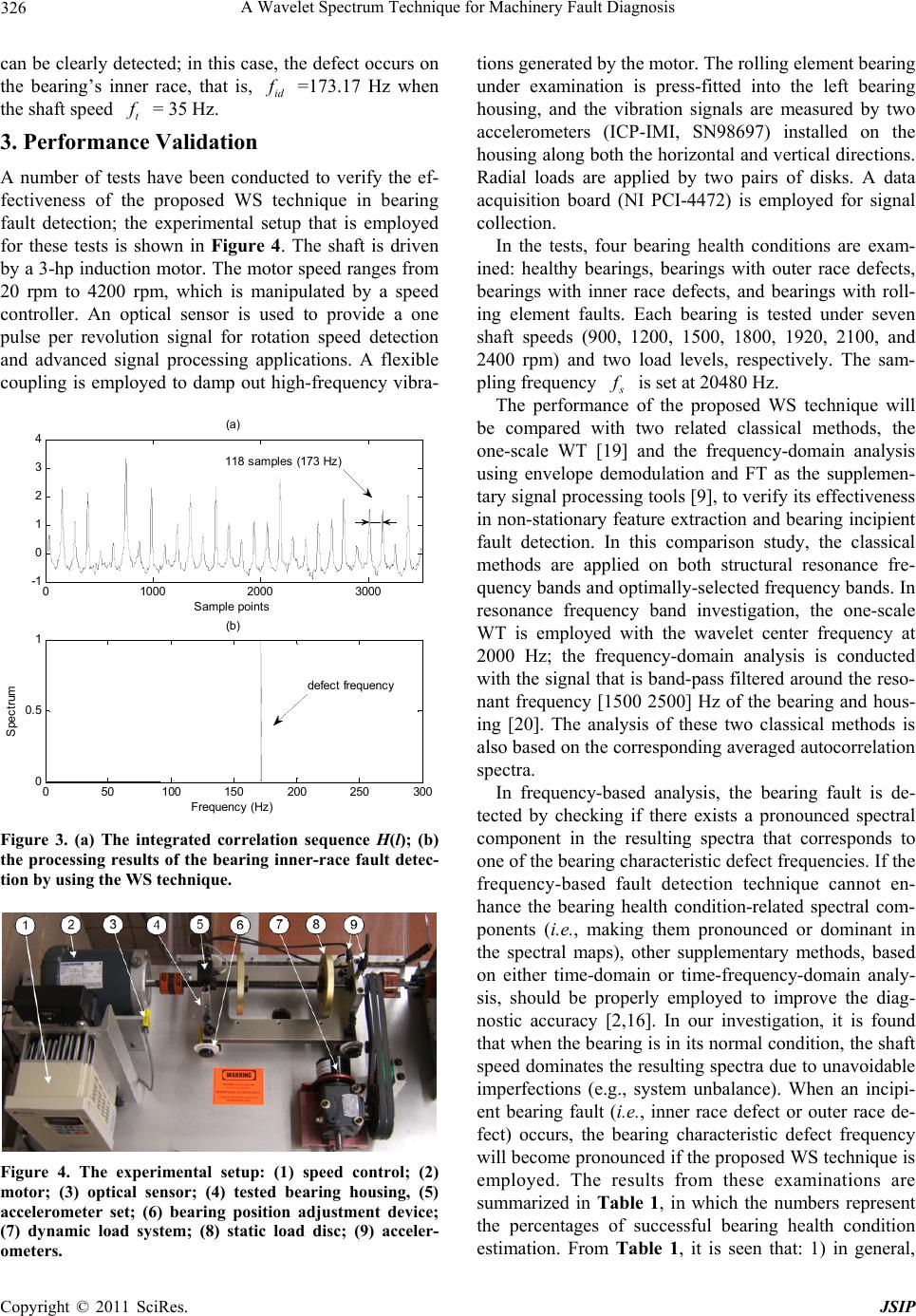

A Wavelet Spectrum Technique for Machinery Fault Diagnosis 326
can be clearly detected; in this case, the defect occurs on
the bearing’s inner race, that is, =173.17 Hz when
the shaft speed = 35 Hz.
id
f
t
f
3. Performance Validation
A number of tests have been conducted to verify the ef-
fectiveness of the proposed WS technique in bearing
fault detection; the experimental setup that is employed
for these tests is shown in Figure 4. The shaft is driven
by a 3-hp induction motor. The motor speed ranges from
20 rpm to 4200 rpm, which is manipulated by a speed
controller. An optical sensor is used to provide a one
pulse per revolution signal for rotation speed detection
and advanced signal processing applications. A flexible
coupling is employed to damp out high-frequency vibra-
01000 20003000
-1
0
1
2
3
4(a)
S am pl e poi nt s
050 100 150 200250 300
0
0.5
1(b)
Frequen cy (H
Spectrum
z)
118 s (173 Hz )ampl es
defect frequenc y
Figure 3. (a) The integrated correlation sequence H(l); (b)
the processing results of the bearing inner-race fault detec-
tion by using the WS technique.
Figure 4. The experimental setup: (1) speed control; (2)
motor; (3) optical sensor; (4) tested bearing housing, (5)
accelerometer set; (6) bearing position adjustment device;
(7) dynamic load system; (8) static load disc; (9) acceler-
ometers.
tions generated by the motor. The rolling element bearing
under examination is press-fitted into the left bearing
housing, and the vibration signals are measured by two
accelerometers (ICP-IMI, SN98697) installed on the
housing along both the horizontal and vertical directions.
Radial loads are applied by two pairs of disks. A data
acquisition board (NI PCI-4472) is employed for signal
collection.
In the tests, four bearing health conditions are exam-
ined: healthy bearings, bearings with outer race defects,
bearings with inner race defects, and bearings with roll-
ing element faults. Each bearing is tested under seven
shaft speeds (900, 1200, 1500, 1800, 1920, 2100, and
2400 rpm) and two load levels, respectively. The sam-
pling frequency
s
f is set at 20480 Hz.
The performance of the proposed WS technique will
be compared with two related classical methods, the
one-scale WT [19] and the frequency-domain analysis
using envelope demodulation and FT as the supplemen-
tary signal processing tools [9], to verify its effectiveness
in non-stationary feature extraction and bearing incipient
fault detection. In this comparison study, the classical
methods are applied on both structural resonance fre-
quency bands and optimally-selected frequency bands. In
resonance frequency band investigation, the one-scale
WT is employed with the wavelet center frequency at
2000 Hz; the frequency-domain analysis is conducted
with the signal that is band-pass filtered around the reso-
nant frequency [1500 2500] Hz of the bearing and hous-
ing [20]. The analysis of these two classical methods is
also based on the corresponding averaged autocorrelation
spectra.
In frequency-based analysis, the bearing fault is de-
tected by checking if there exists a pronounced spectral
component in the resulting spectra that corresponds to
one of the bearing characteristic defect frequencies. If the
frequency-based fault detection technique cannot en-
hance the bearing health condition-related spectral com-
ponents (i.e., making them pronounced or dominant in
the spectral maps), other supplementary methods, based
on either time-domain or time-frequency-domain analy-
sis, should be properly employed to improve the diag-
nostic accuracy [2,16]. In our investigation, it is found
that when the bearing is in its normal condition, the shaft
speed dominates the resulting spectra due to unavoidable
imperfections (e.g., system unbalance). When an incipi-
ent bearing fault (i.e. , inner race defect or outer race de-
fect) occurs, the bearing characteristic defect frequency
will become pronounced if the proposed WS technique is
employed. The results from these examinations are
summarized in Table 1, in which the numbers represent
the percentages of successful bearing health condition
estimation. From Table 1, it is seen that: 1) in general,

A Wavelet Spectrum Technique for Machinery Fault Diagnosis327
Table 1. Comparison of diagnostic results using different
methods.
One-scale
WT
Frequency
analysis WS
Healthy bearing 64.3% 71.4% 100%
Bearing with outer race defect 85.7% 85.7% 100%
Bearing with inner race defect 50.0% 57.1% 92.9%
the classical methods with entropy-based frequency band
selection can be more reliable in detecting a bearing fault
than those methods focusing only on structural resonance
frequency band; 2) the proposed WS outperforms these
two classical methods in terms of bearing fault diagnostic
accuracy, no matter which frequency band is examined.
In the following context, the processing results from one
testing case will be used, as an example, to compare the
performance of different bearing fault detection tech-
niques.
Healthy Bearing: As mentioned earlier, when the
bearing is in its normal condition, the shaft speed domi-
nates the resulting spectra due to some unavoidable shaft
imperfections (e.g., unbalance) and the varying compli-
ance. For example, Figures 5(a)-7(a) show the respec-
tive processing results from these three methods for a
healthy bearing (t = 35 Hz). It is seen that the shaft
speed can be clearly recognized by using the WS tech-
nique (Figure 5(a)). By contrast, the shaft speed infor-
mation can not be clearly identified by using the
one-scale WT and the frequency-domain analysis (Fig-
ures 6(a) and 7(a)); instead, the third harmonic of the
shaft speed dominates the resulting spectra (Figures 6(a)
and 7(a)), which is in fact very close to the outer race
defect frequency ( = 106.83 Hz) in this case.
f
od
f
3.1. Outer Race Fault Detection
Outer race fault detection is a relatively easy task be-
cause the ring is fixed and the defect-related resonance
modes do not change dramatically. Table 1 illustrates
that the proposed WS technique can detect the outer race
faults in all test cases in which the outer race defect fre-
quency dominates the resulting spectra; one example is
shown in Figure 5(b) when od = 106.83 Hz. It is
noted that the one-scale WT and the employed fre-
quency-domain technique can also detect the outer race
defects although in some test cases the harmonics of the
outer race defect frequency dominate the resulting spec-
tra, as seen in Figures 6(b) and 7(b).
f
3.2. Inner Race Fault Detection
The detection of a fault on an inner race is more chal-
lenging than on a fixed outer ring because the modes of
the generated resonance signatures vary over time. Test
results in Table 1 demonstrate that the WS technique is
more reliable (e.g., Figure 3(b)) than the related classical
0
0. 2
0.4 (a)
Spectrum
0
0. 5
1(b)
Spectrum
050100 150200250 300
0
0. 5
1(c)
Frequenc y (Hz)
Spectrum
shaft speed
defect frequenc y harm oni c
defect frequenc y
shaft speed
s haft speed harm oni c
defect frequenc y
Figure 5. The processing results when the WS technique is
applied: (a) healthy bearing; (b) bearing with an outer race
fault; (c) bearing with a rolling element fault.
0
0.2
0.4 (a)
Spectrum
0
0.5
1(b)
Spectrum
050100 150 200250 300
0
0.5
1(c)
Freque ncy (Hz )
Spectrum
s h aft speed
defec t frequency harm oni c
defec t frequency
s haft s peed
shaft speed ha rm onic
defec t frequency
Figure 6. The processing results when the one-scale WT
technique is applied: (a) healthy bearing; (b) bearing with
an outer race fault; (c) bearing with an inner race fault.
methods (e.g., Figures 6(c) and 7(c)) in detecting bearing
faults on rotating rings and in suppressing the noisy
spectral components. This is because the WS technique is
capable of integrating the periodic features from several
contributive wavelet bands.

A Wavelet Spectrum Technique for Machinery Fault Diagnosis 328
0
0.5
1(a)
S pectrum
0
0.5
1(b)
S pectrum
0
0.5
1(c)
Spectrum
050100 150200 250300
0
0.5
1(d)
S pectrum
Frequency (Hz )
shaft speed
defect frequency
s haft speed
defect frequency
defect frequency harm oni c
s haft speed t hi rd harm oni c
defect frequency
Figure 7. The processing results when the employed fre-
quency-domain technique is applied: (a) healthy bearing; (b)
bearing with an outer race fault; (c) bearing with an inner
race fault; (d) bearing with a rolling element fault.
3.3. Rolling Element Fault Detection
The detection of a rolling element fault for ball bearings
is one of the most challenging tasks in bearing health
condition monitoring, especially when the fault is at its
initial stage. This is because: a) the resonance signatures
generated by a ball defect are non-stationary; and b) the
impacts are random since the defect may not always
strike the races. In our tests, it is found that the rolling
element defect frequency can be detected as long as the
shaft speed is sufficiently high (e.g., over 30 Hz in this
test), although the related defect spectral component is
not the dominant one in the resulting spectra. It is also
seen that the defect frequency processed by using the WS
technique (e.g., Figure 5(c)) is more prominent than
those from the two classical methods (e.g., Figures
6(a)-7(d)).
4. Conclusions
A wavelet spectrum (WS) technique is proposed in this
paper for representative feature extraction and bearing
incipient fault detection. The WS technique performs
feature extraction by demodulating the non-stationary
resonance signatures generated by bearing incipient de-
fects and then correlating the periodic patterns over more
contributive wavelet bands. A Jarque-Bera statistic-based
performance indicator is suggested to guide the wavelet
band selection. The effectiveness of the proposed WS
technique is verified by a series of experiments corre-
sponding to different bearing conditions. Test results
show that the WS technique is an effective approach for
non-stationary feature extraction and bearing fault detec-
tion. It outperforms the related classical methods such as
one-scale wavelet transform and the employed fre-
quency-domain technique.
REFERENCES
[1] M. Patil, J. Mathew and P. Rajendrakumar, “Bearing
Signature Analysis as a Medium for Fault Detection: A
Review,” Journal of Tribology, Vol. 130, No. 1, 2008, pp.
1-7. doi:10.1115/1.2805445
[2] J. Liu, W. Wang and F. Golnaraghi, “An Enhanced Di-
agnostic Scheme for Bearing Fault Detection,” IEEE Tr-
ansactions on Instrumentation and Measurement, Vol. 59,
No.2, 2010, pp. 309-321.
doi:10.1109/TIM.2009.2023814
[3] W. Wang, F. Golnaraghi and F. Ismail, “Condition Moni-
toring of a Multistage Printing Press,” Journal of Sound
and Vibration, Vol. 270, No. 4-5, 2004, pp. 755-766.
doi:10.1016/S0022-460X(03)00209-8
[4] J. R. Stack, T. G. Habetler and R. G. Harley, “Fault-Sig-
nature Modeling and Detection of Inner-Race Bearing
Faults,” IEEE Transactions on Industry Applications, Vol.
42, No. 1, 2006, pp. 61-68.
doi:10.1109/TIA.2005.861365
[5] B. Holm-Hansen, R. Gao and L. Zhang, “Customized
Wavelet for Bearing Defect Detection,” Journal of Dy-
namic Systems, Measurement, and Control, Vol. 126, No.
4, 2004, pp. 740-745.
doi:10.1115/1.1850534
[6] D. Shi, W. Wang and L. Qu, “Defect Detection for Bear-
ings Using Envelope Spectra of Wavelet Transform,”
Journal of Vibration and Acoustics, Vol. 126, No. 4, 2004,
pp. 567-573. doi:10.1115/1.1804995
[7] A. Jardine, D. Lin and D. Banjevic, “A Review on Ma-
chinery Diagnostics and Prognostics Implementing Con-
dition-Based Maintenance,” Mechanical Systems and Sig-
nal Processing, Vol. 20, No. 7, 2006, pp. 1483-1510.
doi:10.1016/j.ymssp.2005.09.012
[8] Y. Choi and Y. Kim, “Fault Detection in a Ball Bearing
System Using Minimum Variance Cepstrum,” Measure-
ment Science and Technology, Vol. 18, No. 5, 2007, pp.
1433-1440. doi:10.1088/0957-0233/18/5/031
[9] P. Mcfadden and J. Smith, “Vibration Monitoring of Roll-
ing Element Bearings by the High-Frequency Resonance
Technique—A Review,” Tribology International, Vol. 17,
No. 1, 1984, pp. 3-10.
doi:10.1016/0301-679X(84)90076-8
[10] Y. Sheen, “An Analysis Method for the Vibration Signal
with Amplitude Modulation in a Bearing System,” Jour-
nal of Sound and Vibration, Vol. 303, No. 3-5, 2007, pp.

A Wavelet Spectrum Technique for Machinery Fault Diagnosis
329
538-552. doi:10.1016/j.jsv.2007.01.035
[11] T. Kaewkongka, Y. Au, R. Rakowski and B. Jones, “A
Comparative Study of Short Time Fourier Transform and
Continuous Wavelet Transform for Bearing Condition
Monitoring,” International Journal of COMADEM, Vol.
6, 2003, pp. 41-48.
[12] B. Kim, S. Lee, M. Lee, J. Ni, J. Song and C. Lee, “A
Comparative Study on Damage Detection in Speed-Up
and Coast-Down Process of Grinding Spindle-Typed Ro-
tor-Bearing System,” Journal of Materials Processing
Technology, Vol. 187-188, No. 12, 2007, pp. 30-36.
doi:10.1016/j.jmatprotec.2006.11.222
[13] J. Antoni and R. Randall, “The Spectral Kurtosis: Appli-
cation to the Vibratory Surveillance and Diagnostics of
Rotating Machines,” Mechanical Systems and Signal Pro-
cessing, Vol. 20, No. 2, 2006, pp. 308-331.
doi:10.1016/j.ymssp.2004.09.002
[14] L. Li and L. Qu, “Cyclic Statistics in Rolling Bearing
Diagnosis,” Journal of Sound and Vibration, Vol. 267,
No. 2, 2003, pp. 253-265.
doi:10.1016/S0022-460X(02)01412-8
[15] W. Wang, F. Ismail and F. Golnaraghi, “A Neuro-Fuzzy
Approach for Gear System Monitoring,” IEEE Transac-
tions on Fuzzy Systems, Vol. 12, No. 5, 2004, pp. 710-723.
doi:10.1109/TFUZZ.2004.834807
[16] K. Al-Raheem, A. Roy, K. Ramachandran, D. Harrison
and S. Grainger, “Application of the Laplace-Wavelet
Combined with ANN for Rolling Bearing Fault Diagno-
sis,” Journal of Vibration and Acoustics, Vol. 130, 2008,
pp. 1-9. doi:10.1115/1.2948399
[17] H. Ocak and K. Loparo, “HMM-Based Fault Detection
and Diagnosis Scheme for Rolling Element Bearings,”
Journal of Vibration and Acoustics, Vol. 127, No. 4, 2005,
pp. 299-306. doi:10.1115/1.1924636
[18] Q. Sun and Y. Tang, “Singularity Analysis Using Con-
tinuous Wavelet Transform for Bearing Fault Diagnosis,”
Mechanical Systems and Signal Processing, Vol. 16, No.
6, 2002, pp. 1025-1041. doi:10.1006/mssp.2002.1474
[19] C. Wang and R. Gao, “Wavelet Transforms with Spectral
Post-Processing for Enhanced Feature Extraction,” IEEE
Transactions on Instrumentation and Measurement, Vol.
52, No. 4, 2003, pp. 1296-1301.
doi:10.1109/TIM.2003.816807
[20] J. Liu, W. Wang and F. Golnaraghi, “An Extended Wave-
let Spectrum for Bearing Fault Diagnostics,” IEEE Trans-
actions on Instrumentation and Measurement, Vol. 57,
No. 12, 2008, pp. 2801-2812.
doi:10.1109/TIM.2008.927211
[21] C. Croux, G. Dhaene and D. Hoorelbeke, “Testing the
Information Matrix Equality with Robust Estimators,”
Journal of Statistical Planning and Inference, Vol. 136,
No. 10, 2006, pp. 3583-3613.
doi:10.1016/j.jspi.2005.02.021
[22] Y. Gel, W. Miao and J. Gastwirth, “Robust Directed
Tests of Normality against Heavy-Tailed Alternatives,”
Computational Statistics & Data Analysis, Vol. 51, No. 5,
2007, pp. 2734-2746. doi:10.1016/j.csda.2006.08.022