Intelligent Control and Automation, 2011, 2, 299-309
doi:10.4236/ica.2011.24035 Published Online November 2011 (http://www.SciRP.org/journal/ica)
An Adaptive Fuzzy Sliding Mode Control Scheme for
Robotic Systems
Abdel Badie Sharkawy*, Shaaban Ali Salman
Mechanical Engineering Department, Faculty of Engineering, Assiut University, Assiut, Egypt
Received August 7, 2011; revised September 1, 2011; accepted September 28, 2011
Abstract
In this article, an adaptive fuzzy sliding mode control (AFSMC) scheme is derived for robotic systems. In the
AFSMC design, the sliding mode control (SMC) concept is combined with fuzzy control strategy to obtain a
model-free fuzzy sliding mode control. The equivalent controller has been substituted for by a fuzzy system
and the uncertainties are estimated on-line. The approach of the AFSMC has the learning ability to generate
the fuzzy control actions and adaptively compensates for the uncertainties. Despite the high nonlinearity and
coupling effects, the control input of the proposed control algorithm has been decoupled leading to a simpli-
fied control mechanism for robotic systems. Simulations have been carried out on a two link planar robot.
Results show the effectiveness of the proposed control system.
Keywords: Sliding Mode Control (SMC), Adaptive Fuzzy Sliding Mode Control (AFSMC), Fuzzy Logic
Control (FLC), Adaptive Laws, Robotic Control
1. Introduction
Performance of many tracking control systems is limited
by variation of parameters and disturbances. This specially
applies for direct drive robots with highly nonlinear dy-
namics and model uncertainties. Payload changes and/or its
exact position in the end effector are examples of uncer-
tainties. The control methodologies that can be used are
ranging from classical adaptive control and robust control
to the new methods that usually combine good properties
of the classical control schemes to fuzzy [1,2], genetic al-
gorithms [3], neuro-fuzzy [4,5] and neural network [6]
based approaches. Classical adaptive control of manipula-
tors requires a precise mathematical model of the system’s
dynamics and the property of linear parameterization of the
system’s uncertain physical parameters [7].
The study of output tracking problems has a long-
standing history. Sliding mode control (SMC) is often fa-
vored basic control approach, because of the insensitivity
to parametric uncertainties and external disturbances [7-10].
The theory is based on the concept of changing the struc-
ture of the controller to achieve a desired response of the
system. By using a variable high speed switching feedback
gain, the trajectory of the system can be forced on a chosen
manifold, which is called sliding surfaces or switching sur-
faces, and remains thereafter. The design of proper switch-
ing surfaces to obtain the desired performance of the sys-
tem is very important and has been the topic of many pre-
vious works [11,12]. With the desired switching surface,
we need to design a SMC such that any state outside the
switching surface can be driven to the switching surface in
finite time. Generally, in the SMC design, the uncertainties
are assumed to be bounded. This assumption may be rea-
sonable for external disturbance, but it is rather restrictive
as far as unmodelled dynamics are concerned.
Nowadays, fuzzy logic control (FLC) systems have been
proved to be able to solve complex nonlinear control prob-
lems. They provide an effective means to capture the ap-
proximate nature of real world. Examples are numerous;
see [13] for instance. While non-adaptive fuzzy control has
proven its value in some applications [1,2,14], it is some-
times difficult to specify the rule base for some plants, or
the need could arise to tune the rule-base parameters if the
plant changes. This provides the motivation for adaptive
fuzzy control, where the focus is on the automatic on-line
synthesis and tuning of fuzzy controller parameters. It
means the use of on-line data to continually “learn” the
fuzzy controller, which will ensure that the performance
objectives are met. This concept has proved to be a prom-
ising approach for solving complex nonlinear control
problems [15,16].
Recently, adaptive fuzzy sliding mode control design has

A. B. SHARKAWY ET AL. 300
drawn much attention of many researchers. Because, con-
trol chattering, an inherent problem associated with SMC,
can evoke un-modeled and undesired high frequency dy-
namics, Ho et al. [17] have proposed an adaptive fuzzy
sliding mode control with chattering elimination for nonli-
near SISO systems. The adaptive laws, however, rely on
the projection algorithms, which can hardly be satisfied in
practical problems. In [18], the authors have established an
adaptive sliding controller design based on T-S fuzzy sys-
tem models. The fuzzy system used is rather complicated
and the upper bound of the uncertainty is needed to synthe-
size the controller. A robust fuzzy tracking controller for
robotic manipulator which uses sliding surfaces in the con-
trol context can be found in [19]. The control scheme,
however, depends heavily on the properties of the dynamic
model of robotic manipulators and similar to [17], the au-
thors use the projection algorithms which have practical
limitations.
More recently, Li and Huang [20] have designed a MI-
MO adaptive fuzzy terminal sliding mode controller for
robotic manipulators. In the first phase of their work, the
fuzzy control part relied on some expert knowledge and a
trial-and-error procedure is needed to determine the output
singletons. In the second phase, they designed an adaptive
control scheme that determines these parameters on-line.
The rule base, however is restricted to five rules per each
joint and the fuzzy singletons should have values within
specified ranges to enforce stability.
In this work, an adaptive fuzzy sliding mode control
(AFSMC) scheme is proposed for robotic systems. The
scheme is based on the universal approximation property of
fuzzy systems and the powerfulness of SMC theory. A one
dimensional adaptive FLC is designed to generate the ap-
propriate control actions so that the system’s trajectories
stick to the sliding surfaces. Adaptive control laws are de-
veloped to determine the fuzzy rule base and the uncertain-
ties. With respect to SMC, the proposed algorithm elimi-
nates the usual assumptions needed to synthesize the SMC
and better performance can be achieved.
The paper is organized as follows. In Section 2, the
equivalent control method is used to derive a SMC for rigid
robots. Section 3 introduces the proposed AFSMC which is
a model free approach. Simulation results which include
comparison between AFSMC and SMC are presented in
Section 4. Section 5 offers our concluding remarks.
2. Sliding Mode Control (SMC) Design
In this Section, the well-developed literature is used to
demonstrate the main features and assumptions needed to
synthesis a SMC for robotic systems. SMC employs a
discontinuous control effort to derive the system trajec-
tories toward a sliding surface, and then switching on
that surface. Then, it will gradually approach the control
objective, the origin of the phase plane. To this end, con-
sider a general n-link robot arm, which takes into ac-
count the friction forces, unmodeled dynamics, and dis-
turbances, with the equation of motion given by
()(,)()()() ()
ds d
M
xx Cxxx GxFxFxTtt


 
 
(1)
where
n
x
R
n
R  
joint angular position vector of the robot;
applied joint torques (or forces);
() nn
M
xR

 inertia matrix, positive definite;
(, )n CxxxR
 effect of Coriolis and centrifugal forces;
() n Gx R gravitational torques;
nn
d
F
R

 diagonal matrix of viscous and/or dynamic
friction coefficient;
() n
s
F
xR vector of unstructured friction effects and
static friction terms;
n
d
TR vector of generalized input due to disturbances
or unmodeled dynamics.
The controller design problem is as follows. Given the
desired trajectories with some (or all) sys-
tem parameters being unknown, derive a control law for
the torque (or force) input
,,, ddd xxx 
()t

such that the position
vector
x
and the velocity vector can track the de-
sired trajectories, if not exactly then closely. For simplic-
ity, let (1) rewritten as:
x

()(,) ()
M
xxf xxt



  (2)
where the vector
(,) (,)()()().

 
 
ds d
f
xxCxxxGxFxF xTt
The following assumptions are needed to synthesis a
SMC:
Assumption 1: The matrix ()
M
x
ˆ()
is bounded by a
known positive definite matrix
M
x.
Assumption 2: There exists a known estimate
for the vector function in (2).
),(
ˆxxf 
),( xxf
The tracking control problem is to force the state vec-
tor to follow desired state trajectories . Let
be the tracking error vector. Further,
let us define the linear time-varying surface [21],
)(txd
)()()( txtxte d 
)(ts
() ()()
s
tet t



,

12
( ,)(),(),,()T
n
s
xts tstst (3)
where and
)()()( txtxte d
  )(t

is a time varying
linear function. Thus from (2) and (3), we can get the
equivalent control (also called ideal controller):
])[(),()( 

  d
eq xxMxxft (4)
where )(t
eq

is equivalently the average value of )(t

which maintains the system’s trajectories (i.e. tracking
errors) on the sliding surface . To ensure that
they attain the sliding surface in a finite time and there-
0)( ts

A. B. SHARKAWY ET AL.301
after maintains the error on the sliding manifold,
generally the control torque
()et
( )t

consists of a low fre-
quency (average) component and a hitting (high
frequency) component

eq

t 
ht

as follows
)t(
ht
)(t
eq
)(t




 (5)
The role of )(t
ht

acts to overcome the effects of the
uncertainties and bend the entire system trajectories to-
ward the sliding surface until sliding mode occurs. The
hitting controller )(
ht t

is taken as [8,21]
)ssgn(K
ht 

(6)
where,

n1
diag, ,
K
kk

12



 
sgn ,sgn
, , and
0
sgn
i
k

, ,


sgn n

s
ss
x
x



)(


sT.
To verify the control stability, let us first get an ex-
pression for . Using (3)-(5), the first derivative of (3)
is:
)(ts


)
)
ht
i
dtxM
tx
tetxs







)(
)(
)(),(
1



d
f
t
t
 
)(
)(
tx
t

,(
(

(7)
Choosing a Lyapunov function
)(
2tsi
.0
)

i st
)[(
1x
0
2
1
1
V1
n
i

)(
1
n
ii
ii
sk
st 
)

(tsi

(8)
and differentiating using (6) and (7), we obtain:
(
2
1
1




i
i
ht
n
isV

)(t
 d
x
i
(9)
which provides an exponentially stable system.
Since the parameters of (2) depend on the manipulator
structure and payload it carries, it is difficult to obtain
completely accurate values for these parameters. In SMC
theory, estimated values are usually used in the control
context instead of the exact parameters. So that (4) can be
written as:
]
ˆ
,(
ˆ
)( 


eq Mxxft (10)
where , are bounded estimates for ,
and respectively. As mentioned earlier in As-
sumption 1 and 2, they are assumed to be known in ad-
vance.
)(
ˆxM
),( xx
),(
ˆxxf )(xM
f
In sliding mode, the system trajectories are governed by
[9]:
,0)( tsi , (11) )n,,1 
So that, the error dynamics are determined by the
function )(t

. If coefficients of )t(

were chosen to
correspond to the coefficients of a Hurwitz polynomial, it
is thus implying that t. This suggests
0)( telim )(t

taking the following form:

 dt)( 21 i
i
i
i
iectec

, with (12)
0, 21 
ii cc
So that, in a sliding manifold, the error dynamics is:
0)()()( 21


tectecte i
i
i
i
i (13)
and the desired performance is governed by the coeffi-
cients and c.
1 2
In summary, the sliding mode control in (5), (6) and (10)
can guarantee the stability in the Lyapunov sense even
under parameter variations. As a result, the system tra-
jectories are confining to the time varying surfaces (3).
With this in hand, the error dynamics is decoupled i.e.
each degree of freedom is dependent on its perspective
error function, (13). The control law (10) however, shows
that the coupling effects have not eliminated since the
control signal for each degree of freedom is dependent on
the dynamics of the other degrees of freedom. Inde-
pendency is usually preferred in practice. Furthermore, to
satisfy the existence condition, a large uncertainty bound
should be chosen in advance. In this case, the controller
results in large implementation cost and leads to chatter-
ing efforts.
c
3. Decoupled Robot Tracking Control Design
In this Section, we propose a fuzzy system that would
approximate the equivalent control (4). The main chal-
lenge facing the application of fuzzy logic is the devel-
opment of fuzzy rules. To overcome this problem, an
adaptive control law is developed for the on-line genera-
tion of the fuzzy rules. The input of the fuzzy system is the
sliding surfaces (3), and the output is a fuzzy controller,
which substitutes for the equivalent (4). With this choice,
no bounds are needed about the system functions. Fur-
thermore, the uncertainties are estimated and continu-
ously compensated for, which means that the hitting
controller ht (6) is adaptively determined on-line. The
coming Subsection gives a brief introduction to fuzzy
logic systems and characterizes them with the type, which
is utilized in this contribution.
u
3.1. Fuzzy Logic Systems
A fuzzy logic system consists of a collection of fuzzy
IF-THEN rules. A one-input one-output fuzzy system has
the following form:
L
Rule :IF is THEN is l
lf
lsA

 (14)
where 1, 2,,

lL is the rule number,
s
and
f

are
respectively, the input and output variables. l
A
is the
antecedent linguistic term in rule ; and l l

, 1,,

lL
is the label of the rule conclusion, a real number called
fuzzy singleton. The conclusion of each rule (control ac-

A. B. SHARKAWY ET AL. 302
tion), a numerical value not a fuzzy set, can be considered
as pre-defuzzified output. Defuzzification maps output
fuzzy sets defined over an output universe of discourse to
a crisp output,
f

. In this work, we have adopted sin-
gleton fuzzifier, product inference, the center-average
defuzzifier which reduces the fuzzy rules (14) into the
following fuzzy logic system:
1
1
()
(, )
()
l
l
Ll
A
l
fL
A
l
s
s
s








(15)
where l
A

is the membership grade of the input into
the fuzzy set l
s
A
. In (15), if l

’s are free (adjustable)
parameters, then it can be rewritten as:
(,) ()
T
f
s
s



 (16)
where 1 (, )
L

 
,
 
1
[( ),()]   
is the parameter vector and
() 
L
T
s
ss is a regression vector given by
1
()
()
()
l
l
lA
L
A
l
s
s
s






(17)
Generally, there are two main reasons for using the
fuzzy systems in (16) as building blocks for adaptive
fuzzy controllers. Firstly, it has been proved that they are
universal approximators [22]. Secondly, all the parame-
ters in ()
s

can be fixed at the beginning of adaptive
fuzzy systems expansion design procedure so that the
only free design parameter vector is

. In this case,
(,)
s

 is linear in parameters. This approach is adopted
in synthesizing the adaptive control law in this paper.
Without loss of generality, Gaussian membership
functions have been selected for the input variables. A
Gaussian membership function is specified by two pa-
rameters

,c

:
2
1
()gaussian(;c, )exp2
l
j
j
jj
A
xc
xx





 




where represents the membership function’s center
and
c

determines its width.
The fuzzy system used in this contribution is one input
one output system, (14). The input of the fuzzy system is
normalized using
L
number of equally spaced Gaussian
membership functions inside the universe of discourse.
Slopes are identical, see Figure 1.
The described fuzzy system is used to approximate the
nonlinear dynamics of robotic systems. In a decoupled
manner, the control action is computed for each degree of
freedom, based on the corresponding sliding surface. The
control actions l

(output singletons) which are con-
1

l
3l
2

l
Ll

3
c
1
c
2
c
L
c
Figure 1. Input fuzzy sets.
oming Subsection, adaptive laws are derived to do this
3.2. The Adaptation Mechanism
Fuzzy systems are universal function approximators.
section, we derive an adaptive control law
to
c
task. The antecedent part is fixed with Gaussian mem-
bership functions.
They can approximate any nonlinear function within a
predefined accuracy if enough rules are used. This im-
plies the necessity of using expert knowledge in the form
of large number of rules and suitable membership func-
tions. Usually trial and error procedure is needed to
achieve the requested accuracy. Assigning parameters of
the fuzzy systems (or some of them) adaptively greatly
facilitates the design (e.g. reduce the number of rules)
and enhances the performance (saves the computation
resources).
In this Sub
determine the consequent part (control actions con-
tained in parameter vector

) of the fuzzy system which
is used to approximate the unknown nonlinear dynamics
of robotic systems. The proposed scheme saves the need
to expert knowledge and tedious work needed to assign
parameters of the fuzzy system. Furthermore, distur-
bances, approximation errors and uncertainties are de-
termined compensate for on-line leading to a stable
closed loop system.
Lyapunov stability analysis is the most popular ap-
proach to prove and evaluate the convergence property
of nonlinear controllers, e.g., sliding mode control, fuzzy
control system. Here, Lyapunov analysis is employed to
investigate the stability property of the proposed control
system. By the universal approximation theorem [22],
there exists a fuzzy controller ),(


s
f in the form of
(16) such that
()t( ,)T
eqif iiiiii
s





 , 1, ,in (18)
where i

is the approximation error and is bounded by
ii
E 

. Employing a fuzzy controller ˆ
ˆ(, )
i
f
ii
s

 to
ate )(t
i
eq
approxim

as
ˆˆ
ˆ(, )T
i
f
ii ii
s



 (19)
where ˆi

is the estimated value of the parameter vector
i

. Now, the SMC in (5) can be rewritten as:
tained in the paramter vector e

should be known. In the

A. B. SHARKAWY ET AL.303
where the fuzzy controller
ˆ
ˆ
()( ,)( )  
ifiiihtii
ts s (20)
ˆ
ˆ(,)


f
iii
s
controller
is designed to
approximate the equivalent()
eqi t

. Define
ˆ
ˆ(, )

  

f
ieqifiii
s, iii
ˆ

 
use (17), then it
is obtained that
 , and
T
i
f
iii





  (21)
An expression for ()
s
t
 can be expressed as follows:
11
11
(,) ()()
()()()
()()(,)()
()()()(,)()
d
d
eq ht
sxt ett
xtx tt
Mx Mxfxxxt
d
M
xMxfxxx



t







 
 


 





(22)
Substituting from (19-21):
1)()(ht
sM xu

 
 (
where
23)
11 22
,,,
TTTT
nn








 
.
() 
Now, assume that
1
M
x

can be approximated by
finite diagonal matrix
known constant posi-
tive de
M
. Unlike constant con-
schemes (see [23,24] for example), this assump-
tion has been taken into accouns follows. Equation (23)
can be rewritten as
trol gain
t a
,()
T
iiihtiiii
s
Mu E  

, 1,,in (24)
where is the su
i
E
certainties. A cont
f
m of approximn errors an
rol goal would on-line
Define a Lyapunov functio
atiod un-
be thedetermi-
nation oits estimate, ˆ()
i
Et. The estimation error is de-
fined by
()Et E
, 1,,in. (25) ˆ()
iii
Et
n as

2
E

2
2
1
(), ,2
n
ii
i
Vs tEs M 






,
,
12
1
22
T
ii i
i ii
ii
M







where and are positive constants. Differentiat-
ing (2ect to time and using (23), it is
(26)
1

5) with
2

resp ob-
tained that

2
,




 
 
T
nii ii
i i
EE
Vs ,,
1
12
,






iii iiiii
i
ii
EssMM
,,
1
1
()
T
nTii ii
iiihti iiiiiii
i
i
EE
sM uEMM

 


 




 

,
2i




,,
1
1
[()]( )
nj
Tii
iiiiiiiihtiiii
i
i
EE
Ms MsuEM





,
2i










To satisfy, the adaptive laws can be selected as
i

20V

1iii
s



 (27)
Using (20)
ˆsgn( )
htii i
uEs (28)
2
ˆ()
iiii
(29) Et Es   


then (22) can be rewritten as


2
) ]
iii i
E sE
2,
1
ˆ
(), ,[sgn(
ˆ
()0
n
ii ii
i
iii
VstEMsEs
E E



,
1
m
ii
isM 






 

 
(3
Therefore, is reduced gradually and the con
system is stabl which means that the system trajectories
converge to tsliding surfaces
0)
trol
2
V
e
he ()
s
t while ˆ

and
re
ˆ E
main boundeNow, if we let

d.
,2
1
ˆ
()
m
iiii
i
ΓtsMEEV
i


 (31)
and integrate


Γt with respect to time, then it is
shown that
is bounded and
is non-incr unded, it implies that
(33)
22
0()d((0), ,)((),,)
 
 (32)
Because

 
tΓVsEVstE
2((0), ,)Vs E


easing and bo
2((),,)Vst E


0
lim( )d
t
tΓ

  
Furthermore,
Γ
 is bounded, so that by Barbalat's
lemma [7], it can be shown that 0( )d0


lim

 tΓ.
esult, the proposed
t
That is, . As a
AFSMC is asym
e retten as follow
ler (34) has two terms;
()st 0 as
pto
0tr
tically stable.
Hence, the control law (18) can bwris
ˆ
,)sgn( )

ifiiiii
utusEs , 1,,.in (34)
ˆ
ˆ
() (
In summary, the adaptive fuzzy sliding mode control-
ˆ
ˆ(, )

fi
us given in (19) with
parameter
the
ˆi

adjusted by (27) an
AFSMC
d the uncertain
ap
nals to the robotic system may result in chattering caused
ties and
proximation bound ˆi E adjusted by (29). By applying
these adaptive laws, the is model free and can
be guaranteed to be stable for any nonlinear system has
the form of (2).
It should be noted that implementing the algorithm
implies that the both error dynamics and control signals
has been decoupled, since each of them is dependent
only on the perspective sliding surface. Unlike SMC, the
proposed AFSMC does not require any knowledge about
the system functions nor their bounds. It adaptively de-
termines and compensates for the unknown dynamics
and external disturbances leading to a stable closed loop
system. Figure 2 shows the main elements of the control
system.
Remark 1. Since the control laws (6) and (34) contain
the sign function, direct application of such control sig-

A. B. SHARKAWY ET AL. 304

 ets  )(
eq
u
ht
u
u
x
d
x

ˆ
E
ˆ
Figure 2. The closed loop control system utilizing AFSMC.
by the signal discontinuity. To overcome this problem,
the control law is smoothed ou
yer
1
x
2
x
1
l
2
l
1
m
2
m
t within a thin boundary

la[7,21] by replacing the sign function by a satu-
ration function defined as:
sgn 1
sat
ii
i
ss
s

 





1
ii
iii
ii
ss







4. Simulation Results
this Section, we simulate the AFSMC and SMC on a
ulation tests are carried out
using MATLAB R2009a, version 7.8 under Windows 7
In
two link robot; Figure 3. SimFigure 3. A two link rigid ro bot.
The friction and disturbance torques were unknown to
the algorithm. Random signals were generated by the
rand function in MATLAB.
The desired trajectories for and were set as:
environment. A two link robot arm with varying loads is
used to generate data in the simulation tests. The arm is
depicted as 2-input, 2-ouput nonlinear system. The con-
trol architecture shown in Figure 2 represents the closed
loop system, in which the robot is the plant to be con-
trolled. The detailed descriptions of the matrices)(xM ,
(,)Cxx
 and )(xG in (1) for this robot are given in Ap-
pendix A. We consider the state variable vector as the
joint positions; i.e. 12
[,]
T
x
xx. They are usually avail-
dbackals through encoders mounted on the
motor shafts.
Link parameters a2 (1)rand,
213 (1)mrand , 11.0 ml and 20.7 ml, where
the mass of lin
able fee sign
1
x2 x
111222
()),
dd
sin() , ()sin(
x
t t A txtA    
with 11.2
A
rad

,21.6 rad

A, 1
1π/2 rads


,
1
2πrad s



.
Initially, the arm is assumed at rest, i.e.
1
0[0,0] rads




T, and position of links as
t
x
[π/12, π/12]
T
x0 rad
t
sition error oo
0[15 ,15  t
e
1
[1.89,5.03]s
, which resulted in initial po-
and velocity error ] degree
T
re
k twrandomly
om nes from
12m

k one
va
0.10.0 . Figure
k tw
ure 4(b).
1
m and lin
o-rand
a) shows t
ue
o 2 m are
umberang
me history
ried; )1(rand is a pseudr
4( heir ti. A ran-
dom disturbance torq has been added to the gravity
torque of lino, such that [0, 7(1)]T
d
T rand , Fig-
Dynamic and static friction torques were se-
lected as follows:
1
5cos() 0
0 3
d
x
F
2
cos()
x


, 1
1.8 sgn()


s
2
1.2 sgn()

x
F
x
0rad
T
AFSMC has been


t
e
The
.
simulated under the following
setermine each
of theo equivale
ttings. Two rules were implemented to de
twnt control components, i.e. 2

L in
(14). Each rule base has
the subscript de
ber. This means that a total
te
one input, i s and one output,
i
eq
 , where tes the joint num-
were used to de-
1, 2i
of 4
no
rules
rmine the two equivalent torques. This is relatively a
quite small number of rules. In a similar study, i.e. adap-
tive fuzzy sliding mode control for nonlinear systems [25],

A. B. SHARKAWY ET AL.305
1
m
2
m
0 1 2 3
2
3
4
0123
0
2
4
6
8
4
2
0
01 2 3
(a) (b)
Figure 4. Mass of links (a) and disturbance (b) profiles.
the rule base consists of 36 ru
freedom system (the inverted
Coefficients of the sliding surf
s and . After few simulation
in
les for a one de
pendulum).
gree of
aces in (12) were picked
a1 2
tests, the learning rates were adjusted as 1[15,1.5]
T
 
and 2[45, 6]
T
 . The estimated errors in (28)
[40,40]T c
function in
[3,3]T c
d (28) has
have been
itiated as ˆ[300,100]
T
E . As mentioned earlier, the
sign(6) anbeen replaced by the
saturation function with 1
i

, 2,1i.
Evhe parameter vectors is given in Figure
5(a). Zeros te their elements. The su-
perscripts denote the rule number, 1 and 2. The rates of
adaptation for the paramece d
olution of t
were used to initia
eter vtors arepicted in Fig-
ur
by the AFSMC. Similar to what we
e 5(b). As it can be noticed, the rate of adaptation of
rule 1 is very close to rule 2 for the same joint. This re-
mark was noticed by the authors from an enlarged version
of Figure 5(b). Time history of the estimated errors is
shown in Figure 6.
With respect to SMC in (5), (6) and (10), we have si-
mulated it under the following settings. The control sys-
tem has been initiated with the same initial conditions (i.e.
e and e
) followed
did with respect to the AFSMC, the sign function in (6)
has been replaced by the saturation function. The gain K
of the hitting controller gain in (6) was set as 70
K
I

ere wh
I
is 22 identity matrix. This value of
K
has
been sel, ected as the maximum
maximum possible rate of
possible onewhich means
convergence. Larger value
hesize the SMC, results in chattering. To syntˆ()
M
xand
ˆ(,)
f
xx
 in (10) were selected as follows: ˆ5
M
I which
means that it is a time-independent matrix and
0.5 02
ˆ
0 0.51dsd
f
xFxFT






where ,
ds
F
F and d T are defined above.
Similar to AFSMC, the friction and disturbance torques
were unknown to the control algorithm. Results are shown
in Figures 7-12. A close look to these Figures shows that
SMC tle. Figure 12
de
the AFwas lit-bit faster than SMC
picts the control signals. In the transient phase, the
maximum input torques of the SMC exhibits larger values
than those of the AFSMC.
In order to quantify the performance of the two con-
trollers, we have used the following three criteria.
1) Integral of the absolute value of error (IAE):
0() df
t
I
AEett
2) Integral of time multiplied by the absolute value of
the error (ITAE)
0() d
f
t
I
TAEte tt

01 2 3
0
5
01 2 3
-0.5
0
0.5
1
2
ˆ

2
1
ˆ

0123
-200
0
200
1
1
ˆ

2
2
ˆ

0123
-20
0
20
2
1
~


2
2
~


1
2
~


1
1
~


(a) (b)
Figure 5. Time history of (a) parameter vectors (i.e. control actions) and (b) adaptation rate.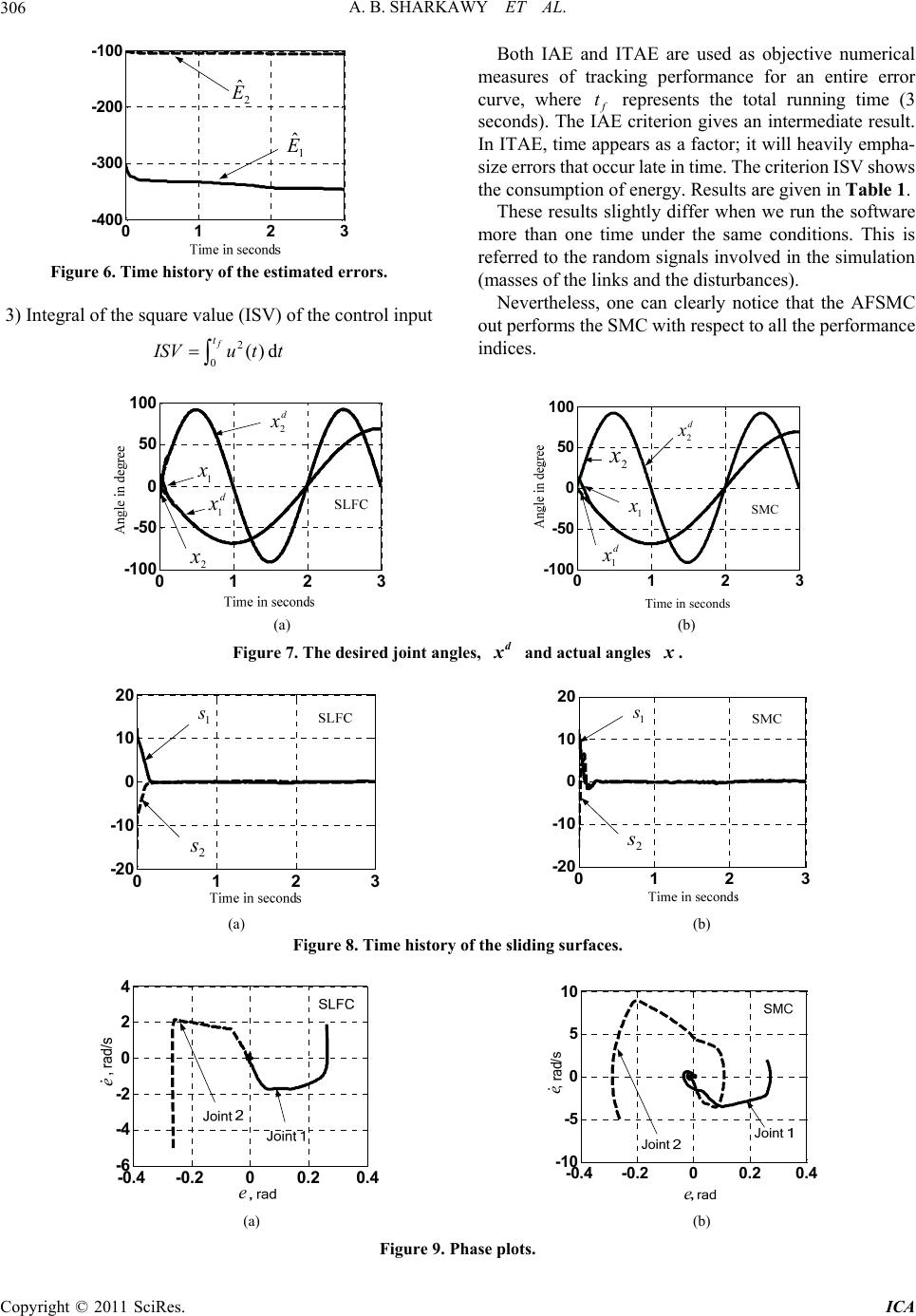

A. B. SHARKAWY ET AL. 306
0 1 23
-400
-300
-200
-100
1
ˆ
E
2
ˆ
E
Figure 6. Time history of the estimated er
Integral of th
rors.
3)e square value (ISV) of the control input
2
0()d
f
t
I
SVut t
Both IAE and ITAE are used as objective numerical
measures of tracking performance for an entire error
curve, where represents the total running time (3
seconds). The criterion gives an intermediate result.
In ITAE, time appears as a factor; it will heavily empha-
size errors that occur late in time. The criterion ISV shows
the consumption of energy. Results are given in Table 1.
These results slightly differ when we run the software
more than one time under the same conditions. This is
o the random signals involved in the simulation
nd the disturbances).
rly notice that the AFSMC
e performance
in
f
t
IAE
referred t
(masses of the links a
Nevertheless, one can clea
out performs the SMC with respect to all th
dices.
0123
100
-100
-50
0
50
1
x
d
x
1
d
x
2
2
x
0 1 2 3
-100
-50
0
50
100
Time in seconds
1
x
d
x
1
SMC
2
x
d
x
2
(b)
, d x and
(a)
Figure 7. The desired joint angles actual angles x.
0 1 2 3
-20
-10
0
10
20
1
s
2
s
0 1 2
3
-20
-10
0
10
20
1
s
2
s
(a) ) (b
Figure 8. Time history of the sliding surfaces.
-0.4 -0.2 00.2 0.4
-6
-4
-2
0
2
4
e
e

-0.4 -0.200.2 0.4
-10
-5
0
5
10
e
e

(a) (b)
Figure 9. Phase plots.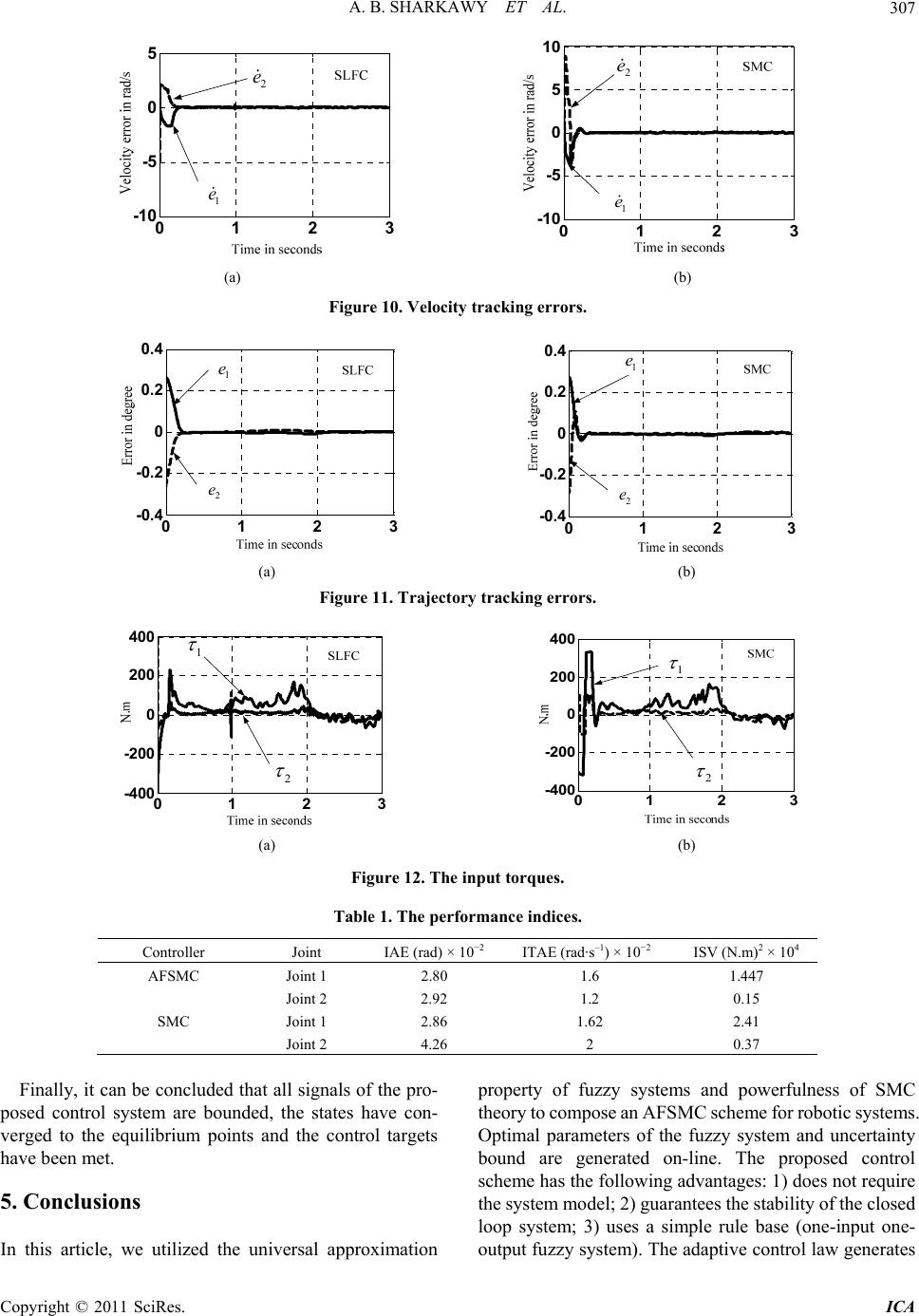

A. B. SHARKAWY ET AL.307
01 2 3
-10
-5
0
5
1
e

2
e 
0 1 23
-10
-5
0
5
10
1
e

2
e

(a) (b)
Figure 10. Velocity tracking errors.
0 12 3
-0.4
-0.2
0
0.2
0.4
1
e
2
e
0123
-0.4
-0.2
0
0.2
0.4
1
e
2
e
(a) (b)
F igure 11. Trajectory tracking errors.
0 1 2 3
-400
-200
0
200
400
1

2

0123
-400
-200
0
200
400
1

2

(a) (b)
Table 1. The perrmance indices.
Controller Joint IAE (rad) × 10− rad·s–1) × 10−2 ISV (N.m)2 × 104
Figure 12. The input torques.
fo
2 ITAE(
AFSMC Joint 1 2.80 1.6 1.447
Joint 2 2.92 1.2 0.15
SMC Joint 1 2.86 1.62 2.41
Joint 2 4.26 2 0.37
Finally, it can be concluded that all signals of the pro-
posed control system are bounded, the states hav
verged to the equilibrium points and the cont
have been met.
5. Conclusions
In this article, we utilized the universal approximation
property of fuzzy systems and powerfulness of SMC
compose an AFSMC scheme for robotic systems.
m and uncertainty
e. The proposed control
he following advantages: 1) does not require
del; 2) guarantees the stability of the closed
) uses a simple rule base (one-input one-
output fuzzy system). The adaptive control law generates
e con-
targets
theory to
Optimal rol parameters of the fuzzy syste
bound are generated on-lin
scheme has t
the system mo
loop system; 3

A. B. SHARKAWY ET AL. 308
on-line the fuzzy rhermore, tcertain
learned on-line and compo
parison with SMC, the proposed cocheme is d
coupled and has elied the assus, which a
usually needed to synthesize a SMC.
The control scheme has been simulated on a two link
pl
uting time, thereby increasing the sam-
ling frequency for possible implementation. It shoul
e developed adaptive laws learn the
zzy rules and uncertainties. Zeros have been used to
ules. Furthe unties are
adaptivelyensated for. In cm-
ntrol se-
minat mptionre
anar robot. The fuzzy system needs only two rules per
joint to determine the control signal. The approach sig-
nificantly eliminates the fuzzy data base burden and re-
duces the comp
pd be
emphasized that, th
fu
initiate them. Results show the effectiveness of the overall
closed-loop system performance.
6. References
[1] A. B. Sharkawy, H. El-Awady and K. A. F. Moustafa,
“Stable Fuzzy Control for a Class of Nonlinear Systems,”
Tranactions of the Institute of Measurement and Control,
Vol. 25, No. 3, 2003, pp. 265-278.
doi:10.1191/0142331203tm086oa
[2] J. Lin, R.-J. Lian, C.-N. Huang and W.-T. Sie, “Enhanced
Fuzzy Sliding Mode Controller for Active Suspension
Systems,” Mechatronics, Vol. 19, No. 7, 2009, pp. 1178-
1190. doi:10.1016/j.mechatronics.2009.03.009
[3] P. C. Chen, C. W. Chen and W. L. Chiang, “GA-Based
Modified Adaptive Fuzzy Sliding Mode Controller for
Nonlinear Systems,” Expert Systems with Applications,
Vol. 36, No. 3, 2009, pp. 5872-5879.
doi:10.1016/j.eswa.2008.07.003
[4] S. Kaitwanidvilai and M. Parnichkun, “Force Control in a
Pneumatic System Using Hybrid Adaptive Neuro-Fuzzy
Model Reference Control,” Mechatronics, Vol. 15, No. 1,
2005, pp. 23-41. doi:10.1016/j.mechatronics.2004.07.003
[5] L.-C. Hung and H.-Y. Chung, “Decoupled Sliding-Mode
with Fuzzy-Neural Network Controller
Systems,” International Journal of
for Nonlinear
Approximate Reason-
o. 1, 2007, pp. 74-97.
jar.2006.08.002
ing, Vol. 46, N
doi:10.1016/j.i
09
[6] Y. Zhiyong, W. Jiang and M. Jiangping, “Motor-Mecha-
nism Dynamic Model Based Neural Network Optimized
Computed Torque Control of a High Speed Parallel Ma-
nipulator,” Mechatronics, Vol. 17, 2007, pp. 381-390.
doi:10.1016/j.mechatronics.2007.04.0
cations in
el and M. Sadeghi,
Mo Slip Control of
Antilock Systems,” Transportation Research Part
C, Vol. 16, No. 6, 2008, pp. 73.
doi:10.1 .trc.2008.02.003
[7] J.-J. Slotine and W. Li, “Applied Nonlinear Control,”
Printice-Hall International, Inc., Upper Saddle River,
1991.
[8] V. I. Utkin, “Sliding Modes and Their Appli
Variable Structure Systems,” Mir Publishers, Moscow,
1978.
[9] V. I. Utkin, “Sliding Modes in Control and Optimiza-
tion,” Springer-Verlag, Berlin, 1992.
[10] A. Harifi, A. Aghagolzadeh, G. Alizad
“Designing a Slidingde Controller for
Brake
1-741
016/j
[11] B. Yao, . Chan and D. W, “Variable Structure
Adaptive Motion and Force C of Robot Manipula-
S. Pang
ontrol
tor,” Automatica, Vol. 30, No. 9, 1994, pp. 1473-1477.
doi:10.1016/0005-1098(94)90014-0
[12] B. Yao, S.P. Chan and D. Wang, “Unified Formulation of
Variable Structure Control Schemes for Robot Manipu-
lators,” IEEE Transactions on Automatic Control, Vol.
39, No. 2, 1994, pp. 371-376. doi:10.1109/9.272337
[13] K. Passino and S. Yurkovich, “Fuzzy Control,” Addison-
Wesley Longman, Inc., Boston, 1998.
[14] R. Ordonez, J. Zumberge, J. T. Spooner and K. M. Pass-
ino, “Adaptive Fuzzy Control: Experiments and Com-
parative Analysis,” IEEE Transactions on Fuzzy Systems,
Vol. 5, No. 2, 1997, pp. 167-188. doi:10.1109/91.580793
[15] F. H. Hsiao, C. W. Chen, Y. W. Liang, S. D. Xu and W
L. Chiang, “T-S Fuzzy Controllers for
.
Nonlinear Inter-
connected TMD Systems with Multiple Time Delays,”
IEEE Transactions on Circuits and Systems, Vol. 52, No.
9, 2005, pp. 1883-1893. doi:10.1109/TCSI.2005.852492
[16] F. H. Hsiao, J. D. Hwang, C. W. Chen and Z. R. Tsai,
“Robust Stabilization of Nonlinear Multiple Time-Delay
Large-Scale Systems via Decentralized Fuzzy Control,”
IEEE Transactions on Fuzzy Systems, Vol. 13, No. 1,
2005, pp. 152-163. doi:10.1109/TFUZZ.2004.836067
[17] H. F. Ho, Y. K. Wong and A. B. Rad, “Adaptive Fuzzy
Sliding Mode Control with Chattering Elimination for
SISO Systems,” Simulation Modeling Practice and The-
ory, Vol. 17, No. 7, 2009, pp. 1199-1210.
doi:10.1016/j.simpat.2009.04.004
C.-C. Cheng and S.-H. Chien[18] , “Adaptive Sliding Mode
Controller Design Based on T-S Fuzzy System Models,”
Automatica, Vol. 42, No. 1, 2006, pp. 1005-1010.
doi:10.1016/j.automatica.2006.02.016
[19] H. F. Ho, Y. K. Wong and A. B. Rad, “Robust Fuzzy
Tracking Control for Robotic Manipulators,” Simulation
Modelling Practice and Theory, Vol. 15, No. 7, 2007, pp.
801-816. doi:10.1016/j.simpat.2007.04.008
[20] T.-H. S. Li and Y.-C. Huang, “MIMO Adaptive Fuzzy
Terminal Sliding-Mode Controller for Robotic Manipu-
lators,” Information Sciences, Vol. 180, No. 23, 2010, pp.
4641-4660. doi:10.1016/j.ins.2010.08.009
[21] Y. Stephaneko and C.-Y. Su, “Variable Structure Control
of Robot Manipulators with Nonlinear Sliding Mani-
folds,” International Journal of Control, Vol. 58, No. 2,
1993, pp. 285-300. doi:10.1080/00207179308923003
[22] L. X. Wang, “Adaptive Fuzzy Systems and Control,”
PTR Prentice Hall, Upper Saddle River, 1994.
[23] S.-J. Huang and W.-C. Lin, “Adaptive Fuzzy Controller
with Sliding Surface for Vehicle Suspension Control,”
IEEE Transactions on Fuzzy Systems, Vol. 11, No. 4,
2003, pp. 550-559. doi:10.1109/TFUZZ.2003.814845
[24] A. Poursamad and A. H. Davaie-Markazi, “Robust Adap-

A. B. SHARKAWY ET AL. 309
tive Fuzzy Control of Unknown Chaotic Systems,” Ap-
plied Soft Computing, Vol. 9, No. 3, 2009, pp. 970-976.
doi:10.1016/j.asoc.2008.11.014
[25] M. Roopaei, M. Zolghadri and S. Meshksar, “Enhanced
Adaptive Fuzzy Sliding mode Control for Uncerta
09,
Nonlinear Systems,” Communications in Nonlinear Sci-
ence and Numerical Simulation, Vol. 14, No. 9-10, 20
pp. 3670-3681. doi:10.1016/j.cnsns.2009.01.029
in
Appendix A
Assuming rigidity of links and joints and using the Lagran
bot arms is given by
ge method, it can be shown that the equation of motion of the
2
ro
11112111 1211
22122221 2
0
M
Mx CCx G
M
Mx CxG


 

 
 
 


here
,
w
22
11121222 1 22
() 2cos
M
mmlmlmllx 
2
1221 22 2122
cos ,
M
Mmlmll x
2
2222 ,
M
ml
112 1 22
sllx 
2
2sinllx  Cm ,x
),
122 1 222
in ,x Cm
212 1 212
sin ,Cmllxx
()cosGmmglx
1121122 12
cos(mgl xx 
222 12
cos( ),Gmgl xx
2
and 9.8 m sec is the acceleration of gravity. g