Int. J. Communications, Network and System Sciences, 2009, 2, 792-796
doi:10.4236/ijcns.2009.28092 blished Online November 2009 (http://www.SciRP.org/journal/ijcns/). Pu
Ant Colony Optimization Based on Adaptive Volatility
Rate of Pheromone Trail
Zhaoquan CAI1, Han HUANG2,3, Yong QIN4, Xianheng MA2
1Educational Technology Center, Huizhou University, Huizhou, China
2School of Software Engineering, South China University of Technology, Guangzhou, China
3State Key Lab for Novel Software Technology, Nanjing University, Nanjing, China
4Center of Information and Network, Maoming University, Maoming, China
Received May 25, 2009; revised July 15, 2009; accepted August 13, 2009
Abstract
Ant colony optimization (ACO) has been proved to be one of the best performing algorithms for NP-hard
problems as TSP. The volatility rate of pheromone trail is one of the main parameters in ACO algorithms. It
is usually set experimentally in the literatures for the application of ACO. The present paper first proposes an
adaptive strategy for the volatility rate of pheromone trail according to the quality of the solutions found by
artificial ants. Second, the strategy is combined with the setting of other parameters to form a new ACO
method. Then, the proposed algorithm can be proved to converge to the global optimal solution. Finally, the
experimental results of computing traveling salesman problems and film-copy deliverer problems also indi-
cate that the proposed ACO approach is more effective than other ant methods and non-ant methods.
Keywords: Ant Colony Optimization (ACO), Adaptive Volatility Rate, Pheromone Trail
1. Introduction
ACO was first proposed by M. Dorigo and his colleagues
as a multi-agent approach to deal with difficult combi-
natorial optimization problems such as TSP [1]. Since
then, a number of applications to the NP-hard problems
have shown the effectiveness of ACO [1]. Up till now,
Ant Colony System (ACS) [2] and MAX-MIN Ant Sys-
tem (MMAS) [3] are so successful and classical that their
strategies such as pheromone global-local update and
Maximum-Minimum of pheromone are widely used in
recent research [1].
The main parameters of ACO may conclude: ,
k

,

and

, where is the number of artificial ants
used for solution construction,
k

is the parameter for
volatility of pheromone trail and ,

 determines the
relative importance of pheromone value and heuristic
information [2,4,5]. All of the parameters are usually set
with experimental methods in the application of ACO
[5–7]. For the adaptive parameter setting, M. Dorigo and
L.M. Gambardella presented a formula for the optimal
number of ants based on the value of k

and in
0
q
ant colony system. I. Watanabe and S. Matsui proposed
an adaptive control mechanism of the parameter candi-
date sets based on the pheromone concentrations [8]. M.
L., Pilat, and T. White put forward the ACSGA-TSP
algorithm [9] with an adaptive evolutionary parame-
ters

,

, and gave the experimental values of
these parameters for some TSP problems. For the pa-
rameters
0
q

and

, which regulate the relative impor-
tance of pheromone trail and closeness [10], H. Huang
proposed a dynamic strategy for a bi-directional search-
ing ant colony system [11]. However, other parameters
should be set experimentally.
This paper presents a trial work of setting the parame-
ters of ACO adaptively. First, a tuning rule for

is
designed based on the quality of the solution constructed
by artificial ants. Then, we introduce the adaptive

to
form a new ACO algorithm, which is tested to compute
several benchmark instances of traveling sales-man
problem and film-copy deliverer problem. Finally, the
experimental result indicates that the new ACS with
adaptive

performs better than GA [12], ACO [13]
and ACS [2,14]. Furthermore, the convergence of the
proposed ACO algorithm is proved.

Z. Q. CAI ET AL. 793
2. Adaptive Volatility Rate of Pheromone
Trail
The framework of ACO [1–2] is inspired by the ants’
foraging behavior in selecting the shortest path between
the nest and the food. Each ant builds a tour (i.e. a feasi-
ble solution to the TSP) by repeatedly applying a sto-
chastic greedy rule (the state transition rule) as Equation
(1) shows.
()
(,)
(,)
[()][] ()
[()][]
()
0
m
k
m
gs rJ g
gt
gs gs
gt
gr gr
tifsJ g
t
Pt
otherwise














(1)
where m
g
s
P is the probability with which the ant
chooses to move from city
m
g
to city in iteration , st

is the pheromone, 1/ d

 is the reciprocal of dis-
tance
g
s
d, and (
m)
J
g is the set of cities not having
been visited yet when ant is at city
m
g
.
After constructing its tour, an artificial ant also modi-
fies the amount of pheromone on the visited edges by
applying the pheromone updating rule. The rule is de-
signed so that it tends to give more pheromone to the
edges which should be visited by ants. The classical
pheromone updating rule is:
(1) (1)()()
gsgs gs
ttt



  (2)
where ()
gs t


(,)
is the increment for the pheromone of
edge
g
s at the -th iteration, and t

is the volatil-
ity rate of the pheromone trail. The optimal

was set
0.1

 experimentally [1,2,4], which means that 90 per
cent of the original pheromone trail remains and its 10
per cent is replaced by the increment.
In order to update the pheromone according to the
quality of solutions found by ants, an adaptive rule for
volatility of the pheromone trail is designed as follows:
111
/( )
mm mP
LLL 

 (3)
where is the length of the solution found by ant
, and
m
Lm
S
m
P
L is the length of the solution
P
S built based
on the pheromone matrix, shown as Equation (4).
()
argmax {[(,)}
m
uJr
s
ru


 (4)
where
s
is the city selected as the next one to city
for any
r
(,)
P
rs S.
The motivation of the proposed rule is: better solutions
should contribute more pheromone, and the worse ones
contribute less. We will use this rule to design a new
ACO algorithm in the following section.
3. An ACO Algorithm with the Adaptive
Parameter
In this section, a new ACO algorithm with the adaptive
rule (shown as Equation 3) is introduced as follows:
Algorithm new ACO
input: An instance of TSP or FDP problems
Initialize solutions and pheromone value.
best SNULL

.
while termination conditions not met do
Construct
P
S
for 1i

to do {k is the number of ar-
tificial ants}
k
()
i
SConstructSolution t

.
i

is calculated based on .
i
S
if () or
(
()( )
i
Length SLength Sbest
L
best
SNUL

) then
best i SS

Endif
Endfor
best

is calculated based on .
best
S
Carry out the pheromone updating rule with
i

(1,...,ik

) and best

.
Endwhile
Output
: .
best
S
End_Algorithm
The framework of the proposed algorithm is similar to
ant colony system (ACS) [2], so are the initialization,
solution construction and setting of the parameters
00.9q

, 10k

, 1


and 2

. There is only an up-
dating rule in the algorithm shown as Equation 5 and 6.
1
(1)(1 )()
g
sigs
tt 

 
ii
L  (5)
where (,) i
g
sS

 and for the
-th iteration.
111
/( )
iii P
LLL 


t
1
(1)(1 )()
g
sbestgsbest best
tt 

 L (6)
where (,)best
g
sS

 and for
the -th iteration.
11
/( )
bestbestbest P
LLL 


1
t
4. Convergence of the Proposed Algorithm
In this section, we give the convergence proof of the new
ACO algorithm.
Given an arbitrary path(,)
g
s,
'
'1
111
1
1(1 )
() (1)()(1)(0)1(1)
t
t
gs grgs
ttU

1
U

 


 
(7)
C opyright © 2009 SciRes. IJCNS

Z. Q. CAI ET AL. 794
Therefore, ()
gs t

has an upper boundary and a lower
boundary, we assume 0()
low gshigh
PtP



where , , 0'tt 111
1minminmax
/( )LLL 

 maxU

, is the length of the worst tour
and is the length of optimal tours.
1
min
),( )}L
min
{(0
gs

L
max
L
with-
out a loss of generality.
'
'2
222
2
1(1 )
()(1 )()(1 )(0)1(1 )
t
t
gs grgs
ttD

2
D

 


 
When is the optimal solution to a n-city TSP
and
*
S
)* (,ab S

as an arbitrary path, the probability
, with which is found by artificial ant in
iteration , can meet:
0
()
( 
ab
Pt (,)ab
00
tt 0
(8) )
where , , 0'tt 111
2maxmaxmin
/( )LLL 

 minD

.
1
max
),( )}L {(0
gs

0
00
0
()
()
() {}()
ab ab
ab
aj aj
jJa
t
PtPq qt







 
 (9)
Because 12
0, 1

, ()
gs
DtU


 when . t
min min
00
00 00
max
0m
() ()
()[ ()][]
() ()[ ]
ab abaalow
ab
ajajhigh ahigh
jJa jJa
tt
Pn ppp
tPkP
min
ax
P




 
 


 




}
(10)
and the results are shown in Table 1. It should be noted
that every instance is computed 20 times. The algorithms
are both programmed in Visual C++6.0 for Windows
System. They would not stop until a better solution could
be found in 500 iterations, which is considered as a vir-
tual convergence of the algorithms.
where [2],
00
{pPqq *
min (, )
min {}
ij
ij S



 and
*
)
max {}
ij
ij S
max (,



.
Given min
00
max
1
low
high
P
ap
kP






0
n
t
, the probability, by
which can be found by ants in iteration , is
, where is the number
of cities. The probability, by which can never be
found from iteration , is:
*
S
(,
0
t
*
*
1
00
)
()( )n
ab
abS
S
PtPn a




0
t
*
S
Table 1 shows that the proposed ACO algorithm
(PACO) performs better than ACS [2] and ACO [13].
The shortest lengths and the average lengths obtained by
PACO are shorter than those found by ACS and ACO in
all of the TSP instances. Furthermore, it can be con-
cluded that the standard deviations of the tour lengths
obtained by PACO are smaller than those of another al-
gorithms. Therefore, we can conclude that PACO is
proved to be more effective and steady than ACS [2] and
ACO [13]. Computation time cost of PACO is not less
than ACS and ACO in all of the instances because it
needs to compute the value of volatility rate 1 k

times
per iteration. Although all optimal tours of TSP problems
cannot be found by the tested algorithms, all of the errors
for PACO are much less than that for another two ACO
approaches. The algorithms may make improvement in
solving TSP when reinforcing heuristic strategies like
local search like ACS-3opt [2] and MMAS+rs [3] are
used.
*
*
0
0
0
~
0
(,)
1
0
() [1( )]
[1] 0
k
ab
Stt ab S
nk
tt
tPP
a





 


(11)
where is the number of artificial ants and can be
arbitrary.
k0 t
Hence, can be found by probability one when the
iteration , which theoretically confirms the capac-
ity of global optimization of the proposed ACO algorithm.
*
S
t
5. Numerical Results FDP problem is an extended style of TSP problem.
Two FDP instances in the literature [14] are computed by
GA-FDP [12], ACS-FDP [14] and the proposed ACO-
FDP on a PC with an Intel Pentium 400MBHz Processor
and 128 MB EMS memory, and the results are shown in
Table 2. It should be noted that every instance is com-
puted 20 times. The algorithms are both programmed in
Visual C++6.0 for Windows System. They would not
stop until a better solution could be found in 500 itera-
tions, which is considered as a virtual convergence of the
algorithms.
This section indicates the numerical results in the ex-
periment that the proposed ACO algorithm is used to
solve TSP problems [15] and FDP problems [14]. Other
approaches for the problems ACS [2], ACO [13], GA-
FDP [12] and ACS-FDP [14] are also tested in the same
machines as the comparison with the proposed ACO.
Several TSP instances are computed by ACS [2], ACO
[13] and the proposed ACO on a PC with an Intel Pen-
tium 550MBHz Processor and 256MB SDR Memory,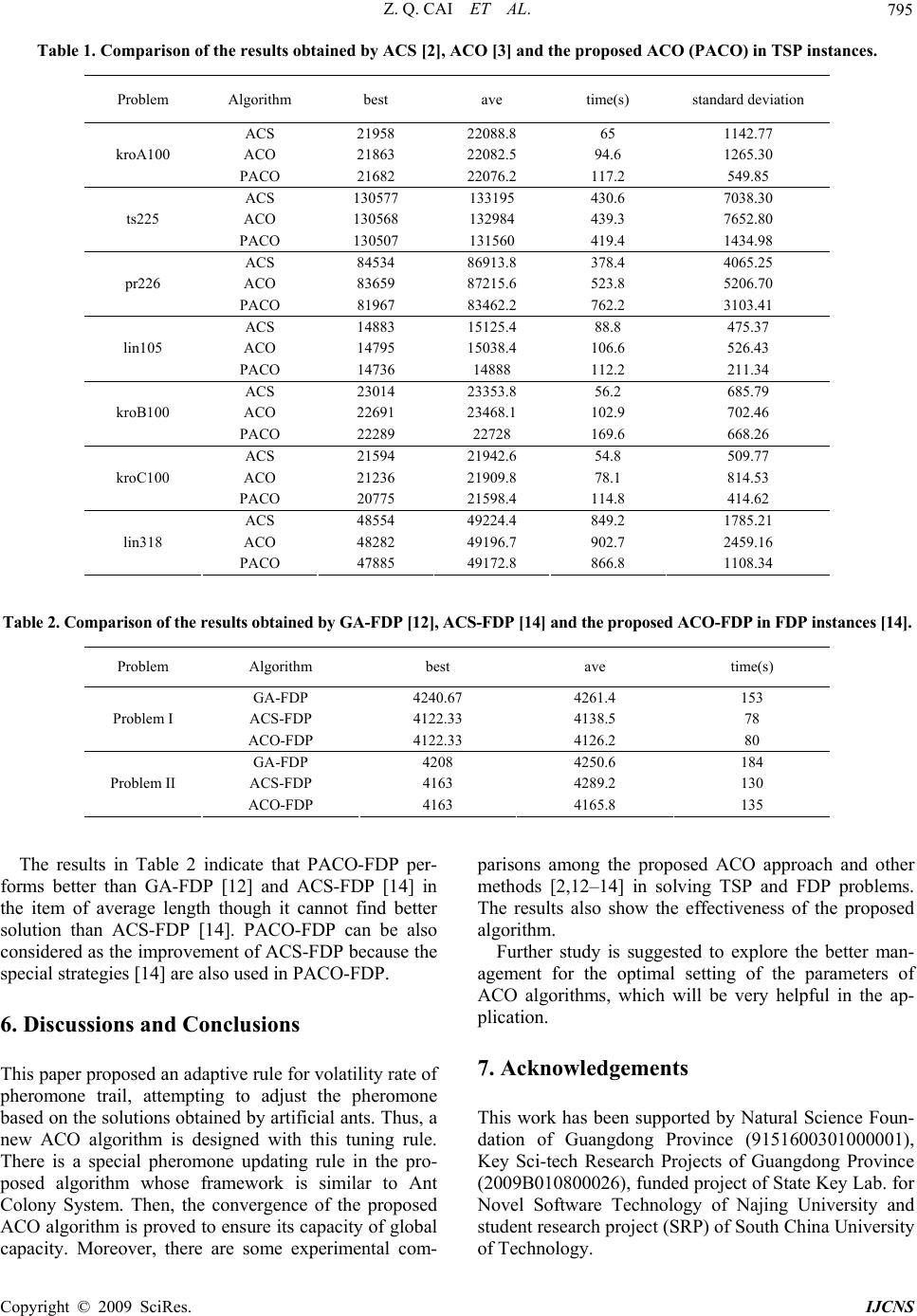

Z. Q. CAI ET AL. 795
Table 1. Comparison of the results obtained by ACS [2], ACO [3] and the proposed ACO (PACO) in TSP instances.
Problem Algorithm best ave time(s) standard deviation
ACS 21958 22088.8 65 1142.77
ACO 21863 22082.5 94.6 1265.30 kroA100
PACO 21682 22076.2 117.2 549.85
ACS 130577 133195 430.6 7038.30
ACO 130568 132984 439.3 7652.80 ts225
PACO 130507 131560 419.4 1434.98
ACS 84534 86913.8 378.4 4065.25
ACO 83659 87215.6 523.8 5206.70 pr226
PACO 81967 83462.2 762.2 3103.41
ACS 14883 15125.4 88.8 475.37
ACO 14795 15038.4 106.6 526.43 lin105
PACO 14736 14888 112.2 211.34
ACS 23014 23353.8 56.2 685.79
ACO 22691 23468.1 102.9 702.46 kroB100
PACO 22289 22728 169.6 668.26
ACS 21594 21942.6 54.8 509.77
ACO 21236 21909.8 78.1 814.53 kroC100
PACO 20775 21598.4 114.8 414.62
ACS 48554 49224.4 849.2 1785.21
ACO 48282 49196.7 902.7 2459.16 lin318
PACO 47885 49172.8 866.8 1108.34
Table 2. Comparison of the results obtained by GA-FDP [12], ACS-FDP [14] and the proposed ACO-FDP in FDP instances [14].
Problem Algorithm best ave time(s)
GA-FDP 4240.67 4261.4 153
ACS-FDP 4122.33 4138.5 78 Problem I
ACO-FDP 4122.33 4126.2 80
GA-FDP 4208 4250.6 184
ACS-FDP 4163 4289.2 130
Problem II
ACO-FDP 4163 4165.8 135
The results in Table 2 indicate that PACO-FDP per-
forms better than GA-FDP [12] and ACS-FDP [14] in
the item of average length though it cannot find better
solution than ACS-FDP [14]. PACO-FDP can be also
considered as the improvement of ACS-FDP because the
special strategies [14] are also used in PACO-FDP.
6. Discussions and Conclusions
This paper proposed an adaptive rule for volatility rate of
pheromone trail, attempting to adjust the pheromone
based on the solutions obtained by artificial ants. Thus, a
new ACO algorithm is designed with this tuning rule.
There is a special pheromone updating rule in the pro-
posed algorithm whose framework is similar to Ant
Colony System. Then, the convergence of the proposed
ACO algorithm is proved to ensure its capacity of global
capacity. Moreover, there are some experimental com-
parisons among the proposed ACO approach and other
methods [2,12–14] in solving TSP and FDP problems.
The results also show the effectiveness of the proposed
algorithm.
Further study is suggested to explore the better man-
agement for the optimal setting of the parameters of
ACO algorithms, which will be very helpful in the ap-
plication.
7. Acknowledgements
This work has been supported by Natural Science Foun-
dation of Guangdong Province (9151600301000001),
Key Sci-tech Research Projects of Guangdong Province
(2009B010800026), funded project of State Key Lab. for
Novel Software Technology of Najing University and
student research project (SRP) of South China University
of Technology.
C opyright © 2009 SciRes. IJCNS

Z. Q. CAI ET AL. 796
8. References
[1] M. Dorigo, G. D. Caro, and L. M. Gambardella, “Ant
algorithms for discrete optimization,” Massachusetts In-
stitute of Technology, Artificial Life 5, pp. 137–172,
1999.
[2] M. Dorigo and L. M. Gambardella, “Ant colony system:
A cooperative learning approach to the traveling sales-
man problem,” IEEE Transactions on Evolutionary
Computation, Vol. 1, No. 1, pp. 53–66, 1997.
[3] T. Stützle and H. H. Hoos, “MAX-MIN ant system, fu-
ture gener,” Computer System, Vol. 16, No. 8, pp. 889–
914, 2000.
[4] M. Dorigo and C. Blum, “Ant colony optimization theory:
A survey,” Theoretical Computer Science, Vol. 344, pp.
243–278, 2005.
[5] A. C. Zecchin, A. R. Simpson, H. R. Maier, and J. B.
Nixon, “Parametric study for an ant algorithm applied to
water distribution system optimization,” IEEE Transactions
on Evolutionary Computation, Vol. 9, No. 2, April 2005.
[6] M. Dorigo and L. M. Gambardella, “Ant colonies for the
traveling salesman problem,” Bio-systems, Vol. 43, pp.
73–81, 1997.
[7] K. M. Sim and W. H. Sun, “Ant colony optimization for
routing and load-balancing: Survey and new directions,”
IEEE Transactions on Systems, Man, and Cybernetics—
Part A: Systems and Humans, Vol. 33, No. 5, September
2003.
[8] I. Watanabe and S. L. Matsui, “Improving the perform-
ance of ACO algorithms by adaptive control of candidate
set, evolutionary computation,” CEC’03, Vol. 2, pp.
1355–1362, 2003.
[9] M. L. Pilat and T. White, “Using genetic algorithms to
optimize ACS-TSP,” M. Dorigo et al. (Eds.):ANTS’02,
LNCS 2463, pp. 282–287, 2002.
[10] L. M. Gambardella and M. Dorigo, “Ant-Q: A rein-
forcement learning approach to the traveling salesman
problem,” Appeared in: Proceedings of ML-95, Twelfth
Intern. Conference on Machine Learning, Morgan Kauf-
mann, pp. 252–260, 1995.
[11] H. Huang and Z. F. Hao, “A bi-directional searching ant
colony system,” Proceedings of 2006 International Con-
ference on Intelligent Systems and Knowledge Engineer-
ing (ISKE’06), April 6-7, 2006.
[12] R. W.Cheng and M. Gen, “Film-copy deliverer problem
using genetic algorithms,” Computers & Industrial Engi-
neering, Vo1. 29, No. l-4, pp. 549–553, 1995
[13] J. Sun, S. W. Xiong, and F. M. Guo, “A new pheromone
updating strategy in ant colony optimization,” Proceed-
ings of 2004 International Conference on Machine
Learning and Cybernetics, Vol. 1, pp. 620–625, 2004.
[14] Z. F.Hao, H. Huang, X. W. Yang, Y. C. Liang, “Solve the
film-copy deliverer problem using ant colony system,”
Proceedings of the Third International Conference on
Machine Learning and Cybernetics, Shanghai, 26-29
August 2004.
[15] G. Reinelt, “A traveling salesman problem library,”
ORSA Journal on Computing, TSPLIB, Vol. 3, No. 4, pp.
376–384, 1991.