Int. J. Communications, Network and System Sciences, 2009, 2, 754-758
doi:10.4236/ijcns.2009.28087 blished Online November 2009 (http://www.SciRP.org/journal/ijcns/).
Pu
Modified Ceiling Bounce Model for Computing Path Loss
and Delay Spread in Indoor Optical Wireless Systems
K. SMITHA 1, A. SIVABALAN 2, J. JOHN 2
1Delphi Technical Center India, Bangalore, India
2Department of Electrical Engineering, Indian Institute of Technology, Kanpur, India
Received July 18, 2009; revised August 18, 2009; accepted September 23, 2009
Abstract
This paper proposes modifications to the tradional Ceiling Bounce Model and uses it to characterize diffuse
indoor optical wireless channel by analyzing the effect of transceiver position on signal propagation
properties. The modified approach uses a combination of the tradional ceiling bounce method and a
statistical approach. The effects of different transmitter-receiver separations and height of the ceiling on path
loss and delay spread are studied in detail.
Keywords: Indoor Optical Channel, Modified Ceiling Bounce Model, Path Loss, Delay Spread
1. Introduction
The increasing demand for high data rates along with
high mobility of data terminals has resulted in the
expanding popularity of optical wireless local area
networks (LANs) [1–3]. The optical spectral region has
plenty of unused unregulated bandwidth making it
possible to establish high bit rate data links. Since optical
signals are blocked by the walls of the rooms, optical
wireless communication systems are secure from eaves-
dropping and interference. The square law photo detector
used at the receiver end is always thousands of times
larger than the wavelength of the light and hence, multi-
path propagation does not produce fading in a direct
detection system.
Among different IR system configurations, the diffuse
topology is the most robust one for local area networks
as it does not require either LOS path between the
transmitter and receiver or strict alignment between them.
The problems associated with such a configuration are
high path loss and intersymbol interference (ISI) due to
multipath dispersion. Multipath propagation results in ISI
because of the spreading out of pulses in time due to the
availability of different paths of varying path lengths for
propagation. This limits the maximum bit rate achie-
vable.
Detailed characterization of multipath medium is esse-
ntial for the successful design of indoor wireless systems.
Modeling and simulation of indoor infrared channel has
been addressed in the literature with the pioneering work
of Gfeller et al. [1,2], who introduced the idea of using
infrared for indoor wireless communications. They
presented a method for determining the power distri-
bution throughout a room given the geometry of the
channel. Barry et al. [4–7] proposed the recursive
method for evaluating the impulse response of an indoor
free-space optical channel with Lambertian reflectors
through which accurate analysis of the effects of mul-
tipath dispersion can be carried out for any multiple
reflections of any order. Perez Jimenez et al. [8,9]
suggested a closed-form expression for the RMS delay
spread which can be used to find the impulse response of
an optical wireless channel, based on several exper-
iments. Carruthers et al. [10] proposed the Ceiling Bou-
nce model which adopts a simple modeling approach
assuming an infinitely large room, i.e. considering only a
single reflection from the transmitter to receiver via
ceiling in the room.
In this paper, we present a detailed characterization of
the indoor optical wireless channel by combining the
statistical approach [8,9] and the traditional ceiling
bounce model [10]. The effect of transmitter and receiver
location on different system features viz., RMS delay
spread, path loss and system bandwidth are analysed in
detail. In Section 2, we define our impulse response
calculation method. Effect of transceiver position on
RMS Delay Spread is discussed in Section 3. Section 4
discusses the effect of transmitter and receiver position

K. SMITHA ET AL. 755
on path Loss. The last section describes the conclusions
of the work.
2. Impulse Response Calculation Using
Modified Ceiling Bounce Approach
For the calculation and analysis the room is assumed to
be empty. It is assumed that the transmitter is pointed
straight upwards and emits a Lambertian pattern which
corresponds to a transmitter semi angle (at half power) of
. The reflecting elements are also assumed to be
perfect Lambertian reflectors with reflectivity between
0.6 and 0.8 [7]. The receiver is assumed to be pointed
straight upward. The transmitter and receiver are located,
respectively, at coordinates (
60
11
,
x
y) and (22 ,
x
y) in the
horizontal (x,y) plane and and represents the
transmitter-ceiling and receiver-ceiling vertical separa-
tions. The room is assumed to be empty. Figure 1
represents the configuration explained above.
1
h2 h
2.1. Traditional Ceiling Bounce Approach
We base our study on the Ceiling Bounce method
developed by Carruthers et al. [10] where the impulse
response of a channel is given by,
67
()=6( )()()
o
htGata ut (1)
where, is called the ceiling bounce
parameter. represents the DC (optical)
gain, is unit function,
=2 /aH
=3
o
GA
()ut
c
2
H 

is the plane reflectivity,
A
the receiver photodiode area, is the separation
distance from the ceiling (transmitter and receiver
assumed to be co-located), and the velocity of light.
H
c
The above model represents the impulse response due
to diffuse reflection from a single infinite plane reflector,
which is a good approximation to a large ceiling. As an
approximation, this model considers only the first
bounce off the ceiling and ignores the higher order
reflections from the walls and ceiling. When the trans-
mitter and receiver are near the center of a large room,
the impulse response of a diffuse configuration is
dominated by the single bounce off the ceiling. When the
Figure 1. Configuration chosen for channel parameter
analysis.
receiver is further separated from the transmitter, the
ceiling no longer appears to the transmitter to be well
approximated by an infinite plane, and the contribution
of the walls to the impulse response will increase relative
to that of the ceiling. This method cannot consider
different separations of transmitter and receiver from the
ceiling. So a new approach is followed in this work to
find the impulse response and the latter channel analysis
using this response.
2.2. Modified Ceiling Bounce Approach
2.2.1. Calculation of RMS Delay Spread
For fixed transmitter and receiver locations, multipath
dispersion is completely characterized by the channel
impulse response . The RMS delay spread
()ht rms

, is
commonly used to quantify the time dispersive properties
of multipath channels .
In this work, the RMS delay spread is calculated
initially using the statistical approach proposed by Perez
Jimenez et al. [8,9]. According to this approach, the
value of rms delay spread depends upon the distance
between transmitter-reflector-receiver d, the transmission
angle between transmitter and receiver

, and mode
number of the source radiation pattern.
The general expression for rms delay is given by [8]
()= ()
rmsnsab coscd
  (2)
For the configuration considered in this paper, after
substituting the statistical parameters, the above equation
becomes [8],
=2.370.007 (0.80.002 )
rms nn
  d
22
2
(3)
The estimated values of rms delay spread obtained
using this closed form expression is very accurate. This
value is used as the parameter in the ceiling bounce
model to find the actual impulse response.
2.2.2. Calculation of Path Loss
The path loss of an unshadowed diffuse configuration
can be estimated using the expression [7]:
22 2
12
22
11 1
22 2
22 2
=
1(()() )
(( )())
oR
Ceiling
GAhh
hxx yy
dx dyhxxyy

 
 
 (4)
The expression assumes a detector field-of-view half
angle of and a Lambertian source. The results
almost follow closely the experimental results, but it
shows variations at large horizontal separations, where
the effect of neglected higher order reflections is
relatively important.
90
C opyright © 2009 SciRes. IJCNS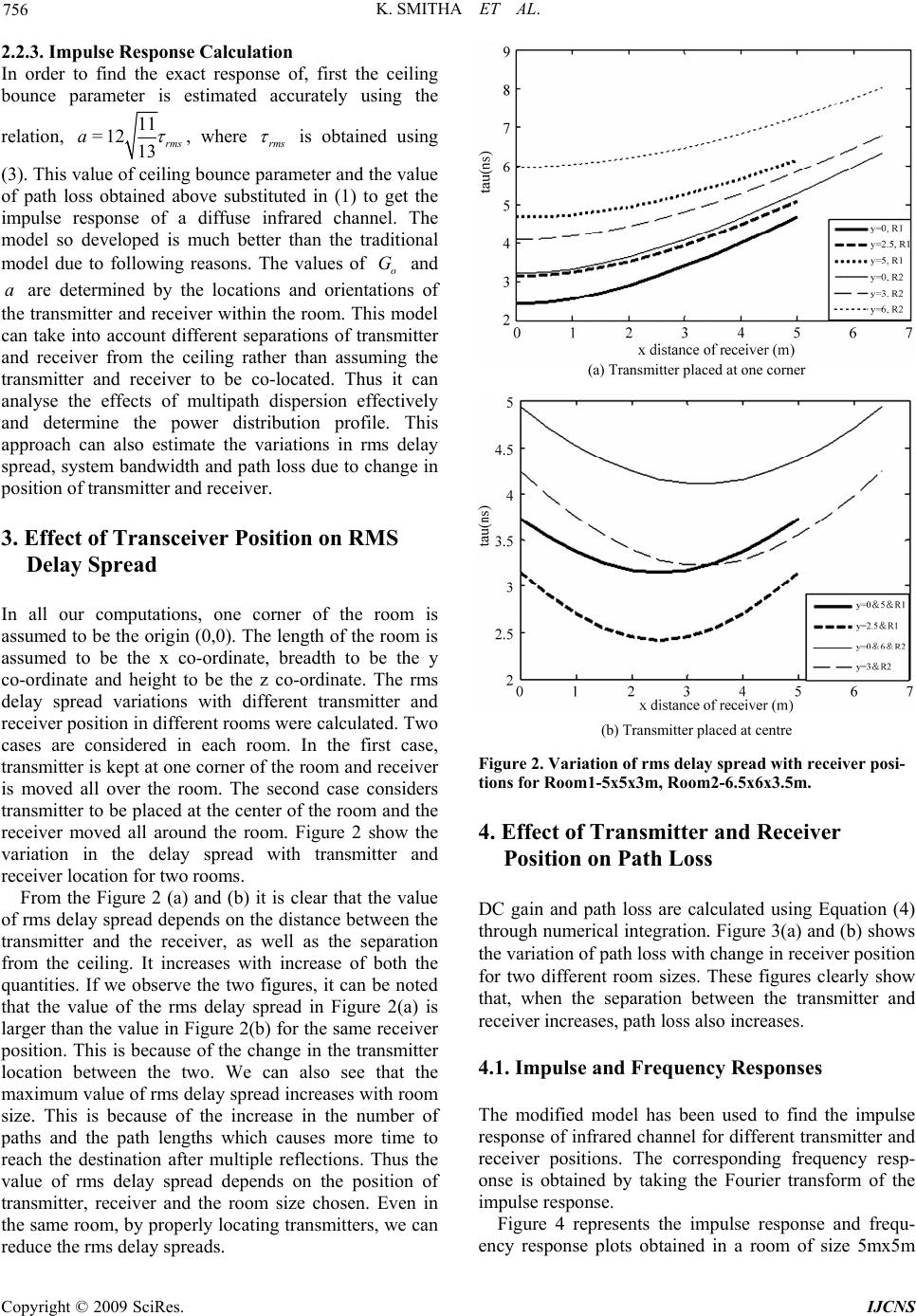

K. SMITHA ET AL. 756
2.2.3. Impulse Response Calculation
In order to find the exact response of, first the ceiling
bounce parameter is estimated accurately using the
relation, 11
=12 13 rms a

, where rms

is obtained using
(3). This value of ceiling bounce parameter and the value
of path loss obtained above substituted in (1) to get the
impulse response of a diffuse infrared channel. The
model so developed is much better than the traditional
model due to following reasons. The values of and
are determined by the locations and orientations of
the transmitter and receiver within the room. This model
can take into account different separations of transmitter
and receiver from the ceiling rather than assuming the
transmitter and receiver to be co-located. Thus it can
analyse the effects of multipath dispersion effectively
and determine the power distribution profile. This
approach can also estimate the variations in rms delay
spread, system bandwidth and path loss due to change in
position of transmitter and receiver.
o
G
a
3. Effect of Transceiver Position on RMS
Delay Spread
In all our computations, one corner of the room is
assumed to be the origin (0,0). The length of the room is
assumed to be the x co-ordinate, breadth to be the y
co-ordinate and height to be the z co-ordinate. The rms
delay spread variations with different transmitter and
receiver position in different rooms were calculated. Two
cases are considered in each room. In the first case,
transmitter is kept at one corner of the room and receiver
is moved all over the room. The second case considers
transmitter to be placed at the center of the room and the
receiver moved all around the room. Figure 2 show the
variation in the delay spread with transmitter and
receiver location for two rooms.
From the Figure 2 (a) and (b) it is clear that the value
of rms delay spread depends on the distance between the
transmitter and the receiver, as well as the separation
from the ceiling. It increases with increase of both the
quantities. If we observe the two figures, it can be noted
that the value of the rms delay spread in Figure 2(a) is
larger than the value in Figure 2(b) for the same receiver
position. This is because of the change in the transmitter
location between the two. We can also see that the
maximum value of rms delay spread increases with room
size. This is because of the increase in the number of
paths and the path lengths which causes more time to
reach the destination after multiple reflections. Thus the
value of rms delay spread depends on the position of
transmitter, receiver and the room size chosen. Even in
the same room, by properly locating transmitters, we can
reduce the rms delay spreads.
(a) Transmitter placed at one corner
(b) Transmitter placed at centre
Figure 2. Variation of rms delay spread with receiver posi-
tions for Room1-5x5x3m, Room2-6.5x6x3.5m.
4. Effect of Transmitter and Receiver
Position on Path Loss
DC gain and path loss are calculated using Equation (4)
through numerical integration. Figure 3(a) and (b) shows
the variation of path loss with change in receiver position
for two different room sizes. These figures clearly show
that, when the separation between the transmitter and
receiver increases, path loss also increases.
4.1. Impulse and Frequency Responses
The modified model has been used to find the impulse
response of infrared channel for different transmitter and
receiver positions. The corresponding frequency resp-
onse is obtained by taking the Fourier transform of the
impulse response.
Figure 4 represents the impulse response and frequ-
ency response plots obtained in a room of size 5mx5m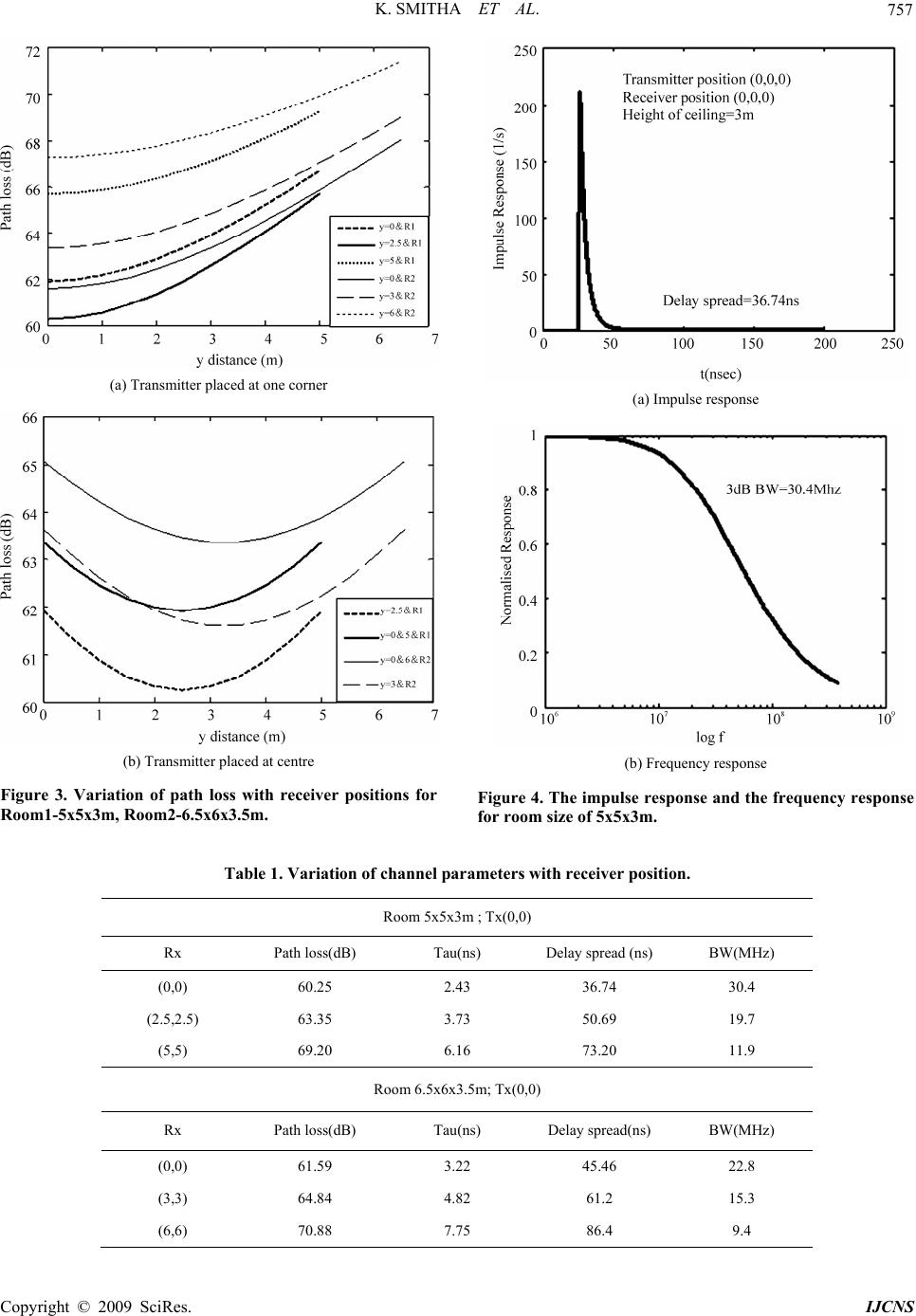

K. SMITHA ET AL. 757
(a) Transmitter placed at one corner
(a) Impulse response
(b) Transmitter placed at centre (b) Frequency response
Figure 3. Variation of path loss with receiver positions for
Room1-5x5x3m, Room2-6.5x6x3.5m.
Figure 4. The impulse response and the frequency response
for room size of 5x5x3m.
Table 1. Variation of channel parameters with receiver position.
Room 5x5x3m ; Tx(0,0)
Rx Path loss(dB) Tau(ns) Delay spread (ns) BW(MHz)
(0,0) 60.25 2.43 36.74 30.4
(2.5,2.5) 63.35 3.73 50.69 19.7
(5,5) 69.20 6.16 73.20 11.9
Room 6.5x6x3.5m; Tx(0,0)
Rx Path loss(dB) Tau(ns) Delay spread(ns) BW(MHz)
(0,0) 61.59 3.22 45.46 22.8
(3,3) 64.84 4.82 61.2 15.3
(6,6) 70.88 7.75 86.4 9.4

K. SMITHA ET AL. 758
x3m. Table 1 shows all the important channel parameters
obtained using the modified ceiling bounce approach in
two rooms of size 5x5x3m and 6.5x6x3.5m. As the
separation between the transmitter and receiver increases,
the system bandwidth also decreases as is evident from
the Table 1. This has effect on the maximum bit rate
achievable. With distance the multipath effects are more
pronounced, which causes a decrease in the bandwidth,
thus resulting in reduction of the maximum bit rate
achievable.
5. Conclusions
Modified ceiling bounce method to find the propagation
properties of the channel is propossed. This method
allows computing impulse response of the diffuse
channel with less computational complexity than the
simple Ceiling bounce model. The influence of
transceiver position on the indoor diffuse channel
parameters is analyzed. Results clearly show that path
loss is a function of separation between the transmitter
and receiver.
6. References
[1] F. R. Gfeller, and U. Bapst, “Wireless in-house data
communication via diffuse infrared radiation,” Pro-
ceedings of IEEE., Vol. 67, pp. 1474–1485, 1979.
[2] F. R. Gfeller, H. R. Muller, and P. Vettiger, “Infrared
communication for in-house applications,” Proceedings
of IEEE Conference on Computer Communication, pp.
132–138, 1978.
[3] Z. Ghassemlooy and A. C. Boucouvalas, “Guest editorial:
Indoor optical wireless communications system and net-
works,” International Journal Communication System,
Vol. 18, pp. 191–193, 2005.
[4] J. R. Barry, J. M. Kahn, W. J. Krause, E. A. Lee, and D.
G. Messerschmitt, “Simulation of multipath impulse
response for wireless optical channels,” IEEE Journal of
Selected Areas on Communication, Vol. 11, pp. 367–379,
April 1993.
[5] J. R. Barry, “Wireless infrared communication,” Boston:
Kluwer, 1994.
[6] J. M. Kahn and J. R. Barry, “Wireless infrared commu-
nications,” Proceedings of IEEE, Vol. 85, pp. 265–298,
February 1997
[7] J. M. Kahn, W. J. Krause, and J. B. Carruthers,
“Experimental characterization of nondirected indoor
infrared channels,” IEEE Transaction Communication,
Vol. 43, pp. 1613–1623, 1995.
[8] R. P. Jimenez, J. Berges, and M. J. Betancor, “Statistical
model for the impulse response of infrared indoor diffuse
channels,” IEE Electronic Letters, Vol. 33, pp. 1298–
1300, 1997.
[9] R. P. Jimenez, V. M. Melian, and M. J. Betancor,
“Analysis of multipath impulse response of diffuse and
quasi-diffuse optical links for IR-WLAN,” Proceedings
of 14th Conference on IEEE Computer Communication
Society, Vol. 1, pp. 924–930, 1995.
[10] J. B. Carruthers and J. M. Kahn, “Modelling of non-
directed wireless infrared channels,” IEEE Transa- ction
on Communication, Vol. 45, pp. 1260–1268, 1997.