Journal of Applied Mathematics and Physics
Vol.06 No.01(2018), Article ID:82287,9 pages
10.4236/jamp.2018.61029
Fractional Difference Approximations for Time-Fractional Telegraph Equation
Ru Liu
College of Information Science and Engineering, Chengdu University, Chengdu, China



Received: September 5, 2017; Accepted: January 28, 2018; Published: January 31, 2018
ABSTRACT
In this paper, we approximate the solution to time-fractional telegraph equation by two kinds of difference methods: the Grünwald formula and Caputo fractional difference.
Keywords:
Time-Fractional Telegraph Equation, the Grünwald Formula, Caputo Fractional Difference

1. Introduction
The classical telegraph equation has another name of the transmission line equation. Because it is originated from the variational relationship between the voltage wave and the current wave on the well-proportioned transmission line, such equation can describe the ordinary diffusion phenomena well. However, when comes to the abnormal diffusion phenomena during the finite long transmits process, where the voltage wave or the current wave possibly exists, the classical telegraph equation cannot describe it well. Fortunately, we have the fractional telegraph equation to handle certain kinds of abnormal diffusion phenomena. For example, R.C. Cascaval [1] investigated several aspects of the fractional telegraph equation, in an effort to better understand the anomalous diffusion process observed in blood flow experiments. Fractional telegraph equation is an telegraph equation where the integer derivative with respect to time or space is replaced by a derivative of fractional order. Furthermore, the fractional telegraph equation is broadly studied to explain the random walks of the suspension flows.
In fact, there are lots of authors who have studied the fractional telegraph equation. E. Orsingher and X. Zhao [2] used the Fourier transform methods to studied the space-fractional telegraph equation. A so-called perturbation Laplace method, a generalized differential transform method and Fourier sin and cos transforms were used by Y. Khan [3], M. Gar [4] and S. Zhang [5] to study fractional telegraph equations, respectively. S. Das [6] used homotopy analysis method, an effective approximate analytical mathematical tool, to solve fractional telegraph equation. W. Jiang [7] obtained the exact solution to the time-fractional telegraph equation with Robin boundary value conditions by using the reproducing kernel theorem. While, A. Ansari [8] used the Bromwich integral for the inverse Melin transform to find an integral representation for a fractional exponential operator, which can be applied to obtain a formal solution of the time-fractional telegraph equation. The Adomian decomposition method was used by S. Momani [9] to achieve analytic and approximate solutions to the space and time fractional telegraph equation. By using a method of separating variables, J. Chen [10] solved a time-fractional telegraph equation with three kinds of nonhomogeneous boundary conditions, namely, Dirichlet, Neumann, Robin boundary conditions. Mittag-leffler functions and generalized Mittag-leffler functions are very important to fractional differential equations. And, S. Yakubovich [11] and R.F. Camargo [12] used them to study fractional telegraph equations.
Orsingher and Beghin [13] obtained the Fourier transform of the fundamental solutions to time-fractional telegraph equations of order 2α. For the special case , they gave the exact representation of the fundamental solution and showed that it was the distribution of a telegraph process with Brownian time. In this paper, we will consider the numerical solutions to this equation.
Actually, some authors have already studied the numerical solutions to some kinds of time or space fractional telegraph equations, such as C. Li [14], Z. Zhao [15], N. J. Ford [16], A. Sevimlican [17], and M. Dehghan [18]. The fractional telegraph equation we consider here is different from all of which they discussed in their papers. Moreover, we will use some other difference methods which are different from what they used, too.
What we will discuss is the following time-fractional telegraph equation [13]:
(1.1)
where , the coefficient .
For , We have the initial conditions,
(1.2)
While, for , besides the condition (1.2), condition
is added.
As for the boundary condition, we consider the Dirichlet boundary condition,
The fractional derivatives appearing in (1.1) is in the sense of Caputo, that is
where 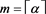 and
.
and
.
2. The Difference Method
In this section, we introduce the basic ideas for the numerical solution to the time-fractional telegraph Equation (1.1) by difference scheme.
For some positive integers M and N, the grid sizes in space and time for the finite difference algorithm are defined by and , respectively. The grid points in the space interval are the numbers and the grid points in the time interval are labeled . We denote the values of the function U at the grid points by . U which is the numerical solution to Equation (1.1) can approximate its exact solution u.
2.1. The Grünwald Formula
According to [[19], (2.36) and (2.37)], we have the following difference schemes which is accurate of order . To obtain the initial values, we use the method of explicit difference.
Firstly, if , then
(2.3)
where . Arranging the system above, we have
We can write the system above in matrix form,
(2.4)
where , and , ,
Here and are the matrices of the following form,
where .
Remark 2.1. All the elements above the diagonal line of the matrix are zero, as well as the elements other than elements on the diagonal line of matrix .
Secondly, if , then
(2.5)
Similarly, we can write the above system into the form of matrix,
Here and are the matrices of the following form,
where .
2.2. The Caputo Fractional Difference
Considering the definition of Caputo derivative, we may use the following difference scheme involved in [[20], (21)]. By the method of implicit difference which is more harmonic with the so-called Caputo derivative we use here, we can get the initial values.
When , we have the following system
(2.6)
and arrange the system above,
Writing the system above in matrix form, we know
where , and are the matrices of the following form,
where .
When , we have the following system
(2.7)
Remark 2.2. We give the supplemental initial values without any conflict.
Arranging the system above, we have
Writing the system above in matrix form, we know
where , and , ,
Here and are the matrices of the following form,
where
.
3. Stability and Convergence of the Method
From difference schemes (2.3), (2.5), (2.6) and (2.7), we obtain four couples of matrices. Because every couple of iteration matrices is similar with each other, we take the scheme (2.3) as an example. Treatments of other schemes are the same as treatment of (2.3).
In order to transform the two-step difference scheme in (2.4) into the one-step one, we use the modified Gauss-Elimination method, and transform the Equation (2.4) into the following,
(3.8)
Next we should determine the matrices and above. From , we can choose and . Substitute and into Equation (3.8), then
Writing into the form
we obtain the following equalities
where
Applying the method of analyzing the eigenvalues of the iteration matrices of the schemes, we can obtain the stability.
Let ρ(A) be the spectral radius of a matrix A, which means the maximum of the absolute value of the eigenvalues of the matrix A. We have the following results.
Theorem 3.1. The difference scheme (2.3) is stable.
Proof. From the analysis of pages 24 and 83 in [21], we should prove that .
1) Obviously, .
2) Since
.
3) If , let us calculate .
Because
knowing that and for , we can obtain that . Consequently, we can get our conclusion by induction. □
Remark 3.1. According to the Lax equivalence theorem [22], we can obtain the convergence of the method from stability and consistency of the proposed scheme.
Corollary 3.1. The difference schemes (2.5), (2.6) and (2.7) are all stable and convergent.
Cite this paper
Liu, R. (2018) Fractional Difference Approximations for Time-Fractional Telegraph Equation. Journal of Applied Mathematics and Physics, 6, 301-309. https://doi.org/10.4236/jamp.2018.61029
References
- 1. Cascaval, R.C., Eckstein, E.C., Frota, C.L. and Goldstein, J.A. (2002) Fractional Telegraph Equations. Journal of Mathematical Analysis and Applications, 276, 145-159. https://doi.org/10.1016/S0022-247X(02)00394-3
- 2. Orsingher, E. and Zhao, X. (2003) The Space-Fractional Telegraph Equation and the Related Fractional Telegraph Process. Chinese Annals of Mathematics, 24, 45-56. https://doi.org/10.1142/S0252959903000050
- 3. Khan, Y., Diblik, J., Faraz, N. and kmarda, Z. (2012) An Efficient New Perturbative Laplace Method for Space-Time Fractional Telegraph Equations. Advances in Difference Equations, 2012, 1-9. https://doi.org/10.1186/1687-1847-2012-204
- 4. Garg, M., Manohar, P. and Kalla, S.L. (2011) Generalized Differential Transform Method to Space-Time Fractional Telegraph Equation. International Journal of Differential Equations, 2011, 1-9. https://doi.org/10.1155/2011/548982
- 5. Zhang, S. (2007) Solution of Semi-Boundless Mixed Problem for Time-Fractional Telegraph Equation, Acta Mathematicae Applicatae Sinica, 23, 611-618. https://doi.org/10.1007/s10255-007-0399
- 6. Das, S., Vishal, K., Gupta, P.K. and Yildirim, A. (2011) An Approximate Analytical Solution of Time-Fractional Telegraph Equation. Applied Mathematics and Computation, 217, 7405-7411. https://doi.org/10.1016/j.amc.2011.02.030
- 7. Jiang, W. and Lin, Y. (2011) Representation of Exact Solution for the Time-Fractional Telegraph Equation in the Reproducing Kernel Space. Communications in Nonlinear Science and Numerical Simulation, 16, 3639-3645. https://doi.org/10.1016/j.cnsns.2010.12.019
- 8. Ansari, A. (2012) Fractional Exponential Operators and Time-Fractional Telegraph Equation. Boundary Value Problems, 2012, 1-6. https://doi.org/10.1186/1687-2770-2012-125
- 9. Momani, S. (2005) Analytic and Approximate Solutions of the Space- and Time-Fractional Telegraph Equations. Applied Mathematics and Computation, 170, 1126-1134. https://doi.org/10.1016/j.amc.2005.01.009
- 10. Chen, J., Liu, F. and Anh, V. (2008) Analytical Solution for the Time-Fractional Telegraph Equation by the Method of Separating Variables. Journal on Mathematical Analysis and Applications, 338, 1364-1377. https://doi.org/10.1016/j.jmaa.2007.06.023
- 11. Yakubovich, S. and Rodrigues, M.M. (2012) Fundamental Solutions of the Fractional Two-Parameter Telegraph Equation. Integral Transforms and Special Functions, 23, 509-519. https://doi.org/10.1080/10652469.2011.608488
- 12. Camargo, R.F., de Oliveira, E.C. and VazJr, J. (2012) On the Generalized Mittag-Leffler Function and Its Application in a Fractional Telegraph Equation. Mathematical Physics, Analysis and Geometry, 15, 1-16. https://doi.org/10.1007/s11040-011-9100-8
- 13. Orsingher, E. and Beghin, L. (2004) Time-Fractional Telegraph Equations and Telegraph Processes with Brownian Time. Probability Theory and Related Fields, 128, 141-160. https://doi.org/10.1007/s00440-003-0309-8
- 14. Li, C. and Cao, J. (2012) A Finite Difference Method for Time-Fractional Telegraph Equation. Mechatronics and Embedded Systems and Applications (MESA), 2012 IEEE/ASME International Conference on. IEEE, 314-318. https://doi.org/10.1109/MESA.2012.6275581
- 15. Zhao, Z. and Li, C. (2012) Fractional Difference/Finite Element Approximations for the Time-Space Fractional Telegraph Equation. Applied Mathematics and Computation, 219, 2975-2988. https://doi.org/10.1016/j.amc.2012.09.022
- 16. Ford, N.J., Rodrigues, M.M., Xiao, J. and Yan, Y. (2013) Numerical Analysis of a Two-Parameter Fractional Telegraph Equation. Journal of Computational and Applied Mathematics, 249, 95-106. https://doi.org/10.1016/j.cam.2013.02.009
- 17. Sevimlican, A. (2010) An Approximation to Solution of Space and Time Fractional Telegraph Equations by He’s Variational Iteration Method. Mathematical Problems in Engineering, 2010, 1-11. https://doi.org/10.1155/2010/290631
- 18. Dehghan, M., Yousefi, S.A. and Lotfi, A. (2011) The Use of He’s Variational Iteration Method for Solving the Telegraph and Fractional Telegraph Equations. International Journal for Numerical Methods in Biomedical Engineering, 27, 219-231. https://doi.org/10.1002/cnm.1293
- 19. Bajlekova, E.G. (2001) Fractional Evolution Equations in Banach Spaces. Ph.D. Thesis, Eindhoven University of Technology.
- 20. Nagai, A. (2003) Discrete Mittag-Leffler Function and Its Applications. Publ. Res. Inst. Math. Sci. Kyoto Univ., 1302, 1-20.
- 21. Smith, G.D. (1993) Numerical Solution of Partial Differential Equations: Finite Difference Methods. Oxford Univ. Press.
- 22. Richtmyer, R.D. and Morton, K.W. (1967) Difference Methods for Initial-Value Problems. Interscience, New York.

