Open Journal of Inorganic Non-metallic Materials, 2011, 1, 1-7
doi:10.4236/ojinm.2011.11001 Published Online October 2011 (http://www.SciRP.org/journal/ojinm)
A New Faraday Rotation Measurement Method for the
Study on Magneto Optical Property of PbO-Bi
2
O
3
-B
2
O
3
Glasses for Current Sensor Applications
Qiuling Chen, Qiuping Chen, Shuangbao Wang
Department of Materials Science and Chemical Engineering, Politecnico di Torino, Torino, Italy
Received August 17, 2011; revised September 19, 2011; accepted September 28, 2011
Abstract
MAGNETO-OPTICAL current transformers (MOCT) based on the Faraday Effect provide numerous ad-
vantages over the conventional transformers. However the commonly used materials in MOCT are crystals
that are very expensive and temperature dependence thus will cause many problems for the output signal.
Cost efficient diamagnetic PbO-Bi
2
O
3
-B
2
O
3
(PBB) glass system is fabricated in this study, for the aim of ob-
taining a good candidate glass with high Verdet constant and good temperature resistance to replace crystals.
A home-made optical bench was setup, calibrated and used for measuring the Verdet constant of the fabri-
cated glasses. Glass with composition of 50%PbO-40%Bi
2
O
3
-10%B
2
O
3
in mol showed high Verdet constant
(0.1533 min·G
–1
·cm
–1
) and good value of the figure of merit (0.02635 min·G
–1
), which can be considered as
the ideal candidate for MOCT applications.
Keywords: MOCT, Magnetic Optical Glass, Verdet Constant
1. Introduction
MAGNETO-OPTICAL current transformers (MOCT’s)
based on the Faraday Effect provide numerous advantages
over the conventional transformers. The measurements are
contactless, small volume and cost efficient. It is hopeful
for MOCT can find much wider applications especially in
automobile industry [1,2]. However commonly used
materials for MOCT are crystals which are very expensive
and temperature dependence [3,4]. On the other hand, low
cost glass with good optical-magnetic properties (e.g. high
Verdet constant and figure of merit etc.) is required greatly
[5-7].
Literatures on glasses based on heavy metal oxides for
the above application have been reported [1,2]. Especially
the oxide glasses with lead and bismuth oxides, due to the
big mass and polarizability of ions Pb
2+
and Bi
3+
belong to
diamagnetism glass and has good temperature resistance,
smaller phonon energy and larger refraction indices [2,4]
comparing to borosilicate, phosphate and silicate glasses.
Based on previous study carried out by the authors [1,5], a
PbO-Bi
2
O
3
-B
2
O
3
(PBB) based glass system was chosen
for this study with the aim of obtaining a good candidate
for MOCT design.
Concerning the measurement of Faraday rotation, the
conventional double light way method is complex due to
the use of lock-in amplifier and computer assisted detec-
tor system and so on [8,9]. In this study, a home-made
single light way method was setup, calibrated and used
to measure the Verdet constant of the glass, the advan-
tage of this optical bench is single and low cost: no needs
the lock-in amplifier, the detector is a power meter. The
magnetic field is induced by solenoids on which the cur-
rent will be applied by a DC supplier. Through the opti-
cal bench, the magneto optical properties of the glasses
were studied.
2. Experiments
2.1. Glass Fabrication and Characterization
The compositions of the prepared glass are listed in
Table 1. Synthesis was carried out in ceramic crucibles
in an electric oven at the temperature at around 900˚C
followed with stirring during melting. The melted mass
was poured into a cast brass form and then relief
annealed. Samples used for studies were cut into 10 mm
× 2 mm slides and polished using Logitech PM5. From

Q. CHEN ET AL.
2
many samples of different percantage of oxides, the one
with optimum composition assuring the best optical and
magnetic properties was chosen.
The refractive indexes of samples were measured
using a prism coupling method (Metricon Model 2010
M). The absorption spectra in ultraviolet-visible region
(200 - 2000 nm) were recorded for each sample using a
UV-Visible-IR spectrophotometer (Varian Cary 500).
Optical energy gap for the studied glasses were evaluated
from relation (
 h  )
1/2
= B
1/2
(h  – E
g
), where B
1/2
is the
slope of the absorption edge reflecting the sample dis-
order [10,11] and h is the photon energy. On the absor-
ption edge the slope line was extended and cross onto
horizontal axis (wavelength), the crossing-point means
the absorption threshold wavelength.
Raman spectra were measured using a MKI Renish-
aw Raman spectroscopy equipped with a BH2-UMA
Olympus microscope between 200 cm
–1
to 2000 cm
–1
.
2.2. Faraday Effect Measurements on Glasses
2.2.1. Optical Ben ch Setup
Figure 1 schematically shows the setup for the Verdet
constant measurement. In order to investigate the Fara-
day Effect of the fabricated PBB glasses, a home-made
Faraday Effect test apparatus is built up: a He-Ne laser
with 15 Mw power at 632.8 nm wavelength was used as
the light source, a 100% refection mirror was used to
change the light way to a polarizer which polarized the
incident light beam to pass the glass which was placed in
a 320 turns solenoid. The polarizers, solenoids and po-
wermeter detector are integrated in a dark box (dotted
line) to avoid the background light and reduce the noise
(two polarizers were set in 90˚ to each other in orienta-
tion).
2.2.2. Measurement and Calcul ation
Due to the Faraday rotation, an angle will happened under
the magnetic field B, the output intensity of the current is
different from that of without B. The difference between
Figure 1. Schematic diagram of optical bench set-up for
Faraday rotation measurement, 1. He-Ne Laser; 2. Polarizers;
3. Bulk glass; 4. DC supplier; 5. Solenoide; 6. Power meter.
the two values is named ΔI. The I, I
0
, the rotated angle θ,
and the Verdet constant of glass V, meet the following
relationship:
I = I
0
cos
2
(a + θ) (1)
ΔI = I
0
sin
2
(θ) ∞ I
0
θ
2
(while a = 90˚) (2)
q = VBL (3)
B = µ
0
NI/L
s
(4)
where I is the detected transmission light intensity with-
out magnetic field, I
0
is the original incident light inten-
sity with the magnetic field applied, a is the angle be-
tween two polarizes without magnetic field, L is the
sample length, µ
0
is the constant (1.26 × 10
−6
B·m
−1
), N
is the turns of solenoids, I is the applied current, Ls is the
length of solenoids. Through the detected output light
intensity (I and I
0
), the rotated angle θ could be obtained
according to Equations (1) and (2). B could be obtained
through the Equation (4). And according to Equation (3),
the V can be calculated.
2.2.3. Unifor mi ty Test of Magneti c Field
The magnetic field B was induced by the DC supplier.
The current was set as 1A DC, and the light intensity I
and I
0
, represented the output voltage values from detec-
tor before and after the switch on of the DC circuit, re-
spectively; through the switch on and off the current, a
magnetic field will be induced or disappeared in the so-
lenoid.
The uniformity and homogenous of B inside the sole-
noids was tested using the magnetometer. The length of
solenoid is around 0.2 m. The B in every one centimeter
from the middle of the solenoid to two ends was meas-
ured using magnetometer. Figure 2 shows the distribu-
tion profile of the B in different position of the solenoids.
It can be seen that the inner magnetic field of solenoid is
uniform.
The relationship between applied current I and the
change of B also was measured for the aim of verify the
uniformity of B inside the solenoids. Changing the ap-
plied current, different B in the middle of solenoid was
obtained from magnetometer. Figure 3 shows the changes
of B under different current I. The relationship between
them is a linear which proved again the B inside the so-
lenoids is homogenous and uniform.
2.2.4. C al ibration of Optical B e nc h
Calibration of the set up was performed using a stand-
ard pure silica sample (its Verdet Constant = 0.01352
min·G
–1
·cm
–1
from literatures [9]). Every time before
measuring the glasses, under the same condition the pure
silica was put inside the solenoids, with and without B, the
utput of intensity of current was recorded and calcula- o

Q. CHEN ET AL.
3
Figure 2. Distribution profile of the B in different position of the solenoids.
Figure 3. Magnetic field B vs current I.
3. Results ted. Compare to its value of 0.01352 min·G
–1
·cm
–1
, if the
measured value is not exceed 0.001 error rate, this
proved that the optical bench is ok for use.
Table 1 reports the composition of prepared glasses and

Q. CHEN ET AL.
4
Table 1. Magnetic-optical properties of the PBB glass sam-
ples.
Glass PBB01 PBB2 PBB03 PBB4 PBB5 PBB06
Composition* 50-40-10 40-50-10 20-70-10 35-45-20 15-65-20 25-35-40
V (min·G
–1
·cm
–1
) 0.1533 0.1153 0.1105 0.083 0.0830.0505
Cutoff (nm) 474.85 471.27 469.84 448.38 458.39 406.16
Q (min·G
–1
) 0.026 0.016 0.015 0.014 0.0140.012
T
g
(˚C ) 289 293 292 307 315 327
T
x
-T
g
(˚C ) 81 63 61 100 58 101
n @633nm 2.374 2.357 2.139 2.215 2.0592.002
ρ (g/cm
–3
) 8.33 8.33 8.31 7.85 8.03 6.57
*Composition of PBB is in mol: PbO-Bi
2
O
3
-B
2
O
3
.
their thermal and magneto optical properties, including
the T
g
, refractive index, Verdet constant, cutoff, the fig-
ure of merit and so on. The difference of T
x
and T
g
is
usually used to evaluate the thermal stability of the
glasses, generally speaking, the bigger the difference, the
more stable of the glass.
3.1. UV-Vis and FT-IR Spectra Analysis
Figure 4 shows the absorption spectra in the UV-visible
region of all glasses. The absorption coefficient, cutoff
changed strongly with the glass composition. The cutoff
shifted to longer wavelength with the increasing of total
amount of PbO + Bi
2
O
3
. Glass PBB01 showed the big-
gest cutoff and lower absorption compared with other
samples. Figure 5 shows the FT-IR spectra analysis on
the prepared glasses. PBB01 showed more than 70% of
transmittance during 2000 nm to 4000 nm. The peak
around 3300 nm is due to the OH absorption. With the
increase of PbO and Bi
2
O
3
content, the spectrum exhibits
a shift to longer wavelength.
3.2. Verdet Constants and the Figure of Merit
The magnetic optical property of fabricated glasses is
Figure 4. UV-visible absorption spectra of the PBB glasses.
Figure 5. FT-IR transmittance spectra of the PBB glasses.
evaluated in term of Verdet constant V and the figure of
merit Q. The relationship between V and Q is: Q = V/
 ,
where
 is the absorption coefficient which was obtained
from Figure 4. Table 1 reports the Verdet constant for
all the glass samples, along with their cutoff and figure
of merit. Figure 4 shows the relationship between Verdet
constant and the cutoff. The PBB01 showed the highest
value of Verdet constant e.g. 0.1533 min·G
–1
·cm
–1
, the
largest cutoff wavelength of 474.85 nm and the best Q of
0.02635 min·G
–1
.
3.3. Raman Spectra
The change of glass properties is due to the change of
glass structures. Figure 7 reports the change of structures
for all samples. There are mainly five peaks named as, A
(400 cm
–1
), B (550 cm
–1
), C (710 cm
–1
), D (920 cm
–1
)
and a broad band (E) around 1220 cm
–1
. A significant
change in spectrum both for the shape and intensity was
observed. PBB01 showed the highest intensity of peaks
for A (400 cm
–1
)and B (550 cm
–1
), and PBB06 showed
the lowest intensity of the same peaks.
The presences of different peaks for heavy metal ox-
ides glasses at different wavelength, for example, 300 -
600 cm
–1
, especially vibrations between 380 - 580 cm
–1
due to the bridging anion modes, and 650 - 950 cm
-1
due
to the non-bridging anion modes [12]. Bismuth and lead
cations have similar atomic weight, they have similar
polarization behaviors. The peak A and B in Figure 7
correspond to the “bridge-anion” motion due to symmet-
ric stretch motion of Bi-O-Bi and Pb-O-Pb bridges com-
bined with some Bi-O-Pb.
A broadening at around 1250 cm
–1
which is named as
E peak is attributed mainly to trigonal boron [BO
3
] [13,
14]. With the change of content of B
2
O
3
in the glass, a

5
Q. CHEN ET AL.
slight change for the peak E was also observed.
4. Discussion
Samples with different compositions presented different
thermal and magneto optical properties as showed pre-
viously. The Verdet constant of the glasses, which was
measured using the home-made optical bench, has rela-
tion with the composition, energy gap and cutoff of the
glasses.
4.1. Relationship between Verdet Constant and
Composition
It is know that the Verdet constant of a magnetic-optical
material is related to the electron shell structure of the
atoms in the transparent medium. If the ions have the
electron structure same with inert gas, the applied field
can induce the Zeeman splitting on the ion energy levels.
The resulting rotation of the polarized plane is diamag-
netism, and the rotating angle θ is positive; the applied
field can induce the moment of force of electrons change
in the ions which have unpaired electrons. Basing on the
classical electromagnetism theory [15,16], Bacquerel has
proposed the relationship between the Verdet constant of
a diamagnetic material and the properties of the materials
as shown in the following equation:

d
Ve2mc
d
n


 (5)
Here, V is the Verdet constant, is the refraction
index of the material;
n
ddn

is the dispersion of the
material; e is electron’s electrical quant, m is the electron
mass, c is light speed and λ is the corresponding light
wavelength. From this Equation (5), it can be seen that
Verdet constant of the diamagnetic material becomes
higher when the dispersion of the material increases. In
fact, the presence of heavy metal ions such as Pb
2+
, Bi
3+
in the glasses could contribute greatly to the color dis-
persion of the glasses. Therefore, the increase of the total
amount of these ions in the glasses will not only lead to
the shift of their cutoff, but also the increase of Verdet
constant.
Basing on the quantum theory [7,15] the Verdet con-
stant of the diamagnetic material is also related to the ion
carriers with energy level splitting possibility as demon-
strated in the following formulary (6):
 
2
22
nn
n
V4πvAvvN
2








(6)
Here is the carriers in per unit volume; : fre-
quency of the incident wave;
n
is the frequency of
electrons migration; is parameters correlative with
migration intensity.
N v
v
n
A
The formulary (6) shows that the Verdet constant of a
diamagnetic material is related to the carriers’ concentra-
tion N, in the case of this study, the Pb
2+
and Bi
3+
ions
are the carriers. Therefore glasses containing higher den-
sity of Pb
2+
and Bi
3+
ions such as PBB01 will show
higher Verdet constant.
From the formulary (6), it is also noted that the Verdet
constant of a diamagnetic material has no relationship
with the working temperature. This is ideal for MOCT,
which makes this PBB glass have great advantages over
the currently used crystal for MOCT.
4.2. Relationship between Verdet Constant and
Energy Gap
From Figure 6 and Table 1 , it can be seen that the Ver-
det constant also has relationship with cutoff, and the
cutoff of glass is related to the energy required for the
electron transition of glass network former from unex-
cited states to excited states. Therefore the shift of cutoff
for PBB glasses depended strongly on the change of the
total amount of PbO + Bi
2
O
3
in the glass, which in fact
act as both glass network former and modifiers [1,5]. On
the other hand, with the decrease of B
2
O
3
content which
acts as glass network former, the glass network structure
will be significantly modified, as it can be seen also from
the Raman Spectra in Figure 7 . In fact, heavy metal ions
such like Pb
2+
, and Bi
3+
play important roles in the glass
as network modifiers that weaken the bridged O-B bonds.
With increasing of PbO + Bi
2
O
3
content, an increase of
structural disorder occurred (the PbO could also behavior
as network formers, considering the difference between
PbO and Bi
2
O
3
), and various non-bridged centers inside
the network will be produced. As a consequence the en-
ergy required for breaking down the glass network of OB
bond will be decreased which leads to the shift of the cu-
Figure 6. The relationship between the Verdet constant and
cutoff.

Q. CHEN ET AL.
6
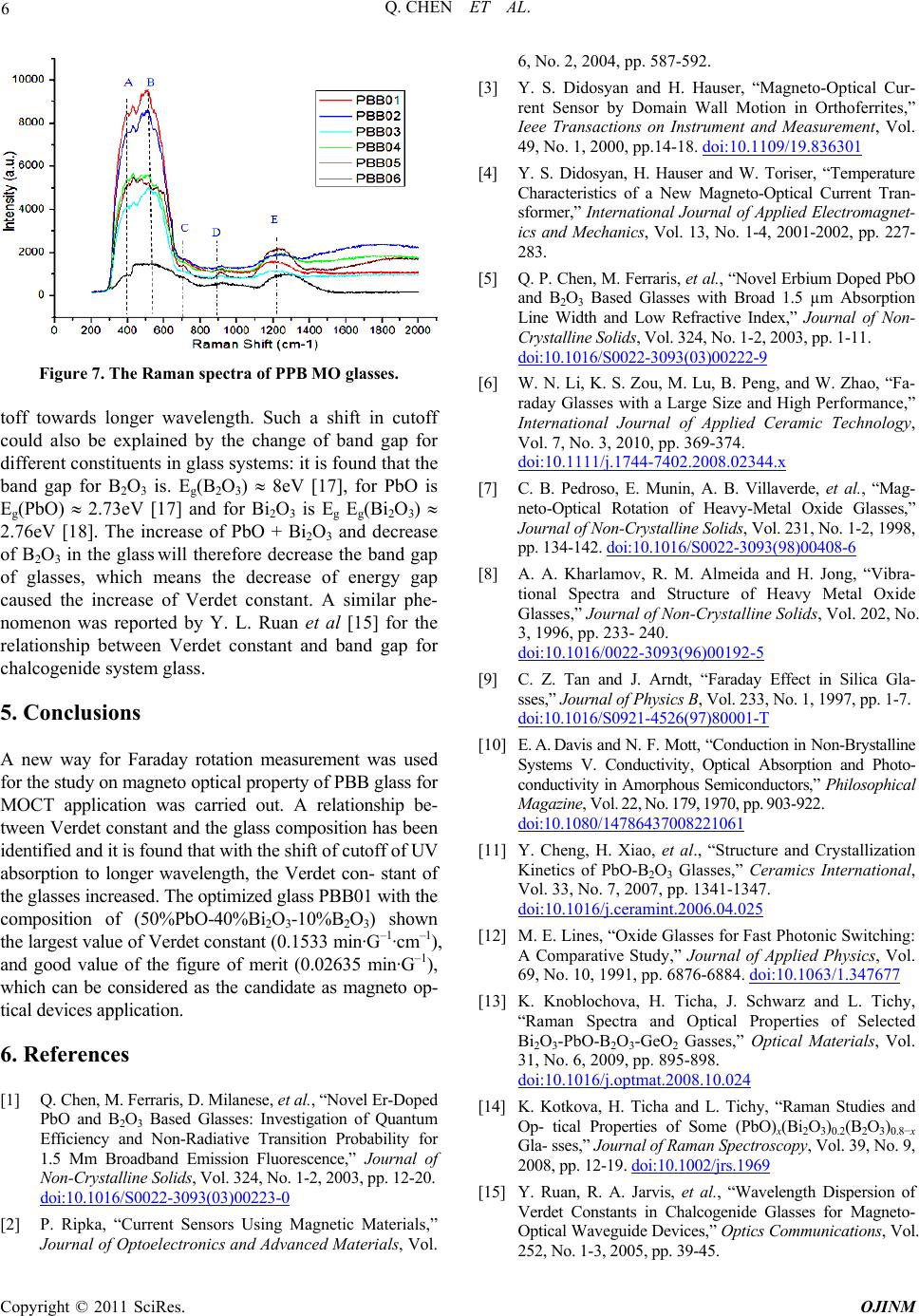
Figure 7. The Raman spectra of PPB MO glasses.
toff towards longer wavelength. Such a shift in cutoff
could also be explained by the change of band gap for
different constituents in glass systems: it is found that the
band gap for B
2
O
3
is. E
g
(B
2
O
3
)  8eV [17], for PbO is
E
g
(PbO)  2.73eV [17] and for Bi
2
O
3
is E
g
E
g
(Bi
2
O
3
) 
2.76eV [18]. The increase of PbO + Bi
2
O
3
and decrease
of B
2
O
3
in the glass will therefore decrease the band gap
of glasses, which means the decrease of energy gap
caused the increase of Verdet constant. A similar phe-
nomenon was reported by Y. L. Ruan et al [15] for the
relationship between Verdet constant and band gap for
chalcogenide system glass.
5. Conclusions
A new way for Faraday rotation measurement was used
for the study on magneto optical property of PBB glass for
MOCT application was carried out. A relationship be-
tween Verdet constant and the glass composition has been
identified and it is found that with the shift of cutoff of UV
absorption to longer wavelength, the Verdet con- stant of
the glasses increased. The optimized glass PBB01 with the
composition of (50%PbO-40%Bi
2
O
3
-10%B
2
O
3
) shown
the largest value of Verdet constant (0.1533 min·G
–1
·cm
–1
),
and good value of the figure of merit (0.02635 min·G
–1
),
which can be considered as the candidate as magneto op-
tical devices application.
6. References
[1] Q. Chen, M. Ferraris, D. Milanese, et al., “Novel Er-Doped
PbO and B
2
O
3
Based Glasses: Investigation of Quantum
Efficiency and Non-Radiative Transition Probability for
1.5 Μm Broadband Emission Fluorescence,” Journal of
Non-Crystalline Solids, Vol. 324, No. 1-2, 2003, pp. 12-20.
doi:10.1016/S0022-3093 (03)002 23-0
[2] P. Ripka, “Current Sensors Using Magnetic Materials,”
Journal of Optoelectronics and Advanced Materials, Vol.
6, No. 2, 2004, pp. 587-592.
[3] Y. S. Didosyan and H. Hauser, “Magneto-Optical Cur-
rent Sensor by Domain Wall Motion in Orthoferrites,”
Ieee Transactions on Instrument and Measurement, Vol.
49, No. 1, 2000, pp.14-18. doi:10.1109/19.836301
[4] Y. S. Didosyan, H. Hauser and W. Toriser, “Temperature
Characteristics of a New Magneto-Optical Current Tran-
sformer,” International Journal of Applied Electromagnet-
ics and Mechanics, Vol. 13, No. 1-4, 2001-2002, pp. 227-
283.
[5] Q. P. Chen, M. Ferraris, et al., “Novel Erbium Doped PbO
and B
2
O
3
Based Glasses with Broad 1.5 µm Absorption
Line Width and Low Refractive Index,” Journal of Non-
Crystalline Solids, Vol. 324, No. 1-2, 2003, pp. 1-11.
doi:10.1016/S0022-3093 (03)002 22-9
[6] W. N. Li, K. S. Zou, M. Lu, B. Peng, and W. Zhao, “Fa-
raday Glasses with a Large Size and High Performance,”
International Journal of Applied Ceramic Technology,
Vol. 7, No. 3, 2010, pp. 369-374.
doi:10.1111/j.1744-7402.2008.02344.x
[7] C. B. Pedroso, E. Munin, A. B. Villaverde, et al., “Mag-
neto-Optical Rotation of Heavy-Metal Oxide Glasses,”
Journal of Non-Crystalline Solids, Vol. 231, No. 1-2, 1998,
pp. 134-142. doi:10.1016/ S0022-3 093(98) 00408-6
[8] A. A. Kharlamov, R. M. Almeida and H. Jong, “Vibra-
tional Spectra and Structure of Heavy Metal Oxide
Glasses,” Journal of Non-Crystalline Solids, Vol. 202, No.
3, 1996, pp. 233- 240.
doi:10.1016/0022-3093(96)00192-5
[9] C. Z. Tan and J. Arndt, “Faraday Effect in Silica Gla-
sses,” Journal of Physics B, Vol. 233, No. 1, 1997, pp. 1-7.
doi:10.1016/S0921-4526 (97)800 01-T
[10] E.
A. Davis and N. F. Mott, “Conduction in Non-Brystalline
Systems V. Conductivity, Optical Absorption and Photo-
conductivity in Amorphous Semiconductors,” Philosophical
Magazine, Vol.
22, No. 179, 1970, pp. 903-922.
doi:10.1080/1478643700 822106 1
[11] Y. Cheng, H. Xiao, et al., “Structure and Crystallization
Kinetics of PbO-B
2
O
3
Glasses,” Ceramics International,
Vol. 33, No. 7, 2007, pp. 1341-1347.
doi:10.1016/j.ceramint.2006.04.025
[12] M. E. Lines, “Oxide Glasses for Fast Photonic Switching:
A Comparative Study,” Journal of Applied Physics, Vol.
69, No. 10, 1991, pp. 6876-6884. doi:10.1063/1.347677
[13] K. Knoblochova, H. Ticha, J. Schwarz and L. Tichy,
“Raman Spectra and Optical Properties of Selected
Bi
2
O
3
-PbO-B
2
O
3
-GeO
2
Gasses,” Optical Materials, Vol.
31, No. 6, 2009, pp. 895-898.
doi:10.1016/j.optmat.2008.10.024
[14] K. Kotkova, H. Ticha and L. Tichy, “Raman Studies and
Op- tical Properties of Some (PbO)
x
(Bi
2
O
3
)
0.2
(B
2
O
3
)
0.8−x
Gla- sses,” Journal of Raman Spectroscopy, Vol. 39, No. 9,
2008, pp. 12-19. doi:10.1002/jrs. 1969
[15] Y. Ruan, R. A. Jarvis, et al., “Wavelength Dispersion of
Verdet Constants in Chalcogenide Glasses for Magneto-
Optical Waveguide Devices,” Optics Communications, Vol.
252, No. 1-3, 2005, pp. 39-45.

Q. CHEN ET AL.
7
doi:10.1016/j.optcom.2 005.03.037
[16] C. B. Peroso, E. Munin, et al., “Magneto-Optical Rotation
of Heavy-Metal Oxide Glasses,” Journal of Non-Crystal-
line Solids, Vol. 231, No. 1-2, 1998, pp. 134-142.
doi:10.1016/S0022-3093 (98)004 08-6
[17] T. Watadabe, K. Muratsubaki, et al., “Hardness and Elas-
tic Properties of Bi
2
O
3
-based Glasses,” Journal of Mate-
rials Science , Vol. 36, No. 10, 2001, pp. 2427-2433.
doi:10.1023/A:1017973830342
[18] E. Munin, A. B. Villaverde, et al., “Magneto-Optical Rota-
tion of Heavy-Metal Oxide Glasses,” Journal of Non-Cry-
stalline Solids, Vol. 231, No. 1-2, 1998, pp. 134-142.
doi:10.1016/S0022-3093 (98)004 08-6
p[