Journal of Information Security, 2011, 2, 139-150
doi:10.4236/jis.2011.24014 Published Online October 2011 (http://www.SciRP.org/journal/jis)
139
New Approach for Fast Color Image Encryption Using
Chaotic Map
Kamlesh Gupta1*, Sanjay Silakari2
1Department of Com p ut er Sci ence, Jaypee University of Engineering and Technology, Guna, India
2Department of Com p ut er Sci ence, Rajiv Gandhi Technical University, Bhopal, I ndia
Received June 6, 2011; revised July 5, 2011; accepted July 16, 2011
Abstract
Image encryption using chaotic maps has been established a great way. The study shows that a number of
functional architecture has already been proposed that utilize the process of diffusion and confusion. How-
ever, permutation and diffusion are considered as two separate stages, both requiring image-scanning to ob-
tain pixel values. If these two stages are mutual, the duplicate scanning effort can be minimized and the en-
cryption can be accelerated. This paper presents a technique which replaces the traditional preprocessing
complex system and utilizes the basic operations like confusion, diffusion which provide same or better en-
cryption using cascading of 3D standard and 3D cat map. We generate diffusion template using 3D standard
map and rotate image by using vertically and horizontally red and green plane of the input image. We then
shuffle the red, green, and blue plane by using 3D Cat map and standard map. Finally the Image is encrypted
by performing XOR operation on the shuffled image and diffusion template. Theoretical analyses and com-
puter simulations on the basis of Key space Analysis, statistical analysis, histogram analysis, Information
entropy analysis, Correlation Analysis and Differential Analysis confirm that the new algorithm that mini-
mizes the possibility of brute force attack for decryption and very fast for practical image encryption.
Keywords: Chaotic Map, 3D Cat Map, Standard Map, Confusion and Diffusion
1. Introduction
With the fast development of image transmission through
computer networks especially the Internet, medical im-
aging and military message communication, the security
of digital images has become a most important concern.
Image encryption, is urgently needed but it is a chal-
lenging task because it is quite different from text en-
cryption due to some intrinsic properties of images such
as huge data capacity and high redundancy, which are
generally difficult to handle by using conventional tech-
niques. Nevertheless, many new image encryption sche-
mes have been suggested in current years, among which
the chaos-based approach appears to be a hopeful direc-
tion.
General permutation-diffusion architecture for chaos-
based image encryption was employed in [1,2] as illus-
trated in Figure 1. In the permutation stage, the image
pixels are relocated but their values stay unchanged. In
the diffusion stage, the pixel values are modified so that
a minute change in one-pixel spreads out to as many pix-
els as possible. Permutation and diffusion are two dif-
ferent and iterative stages, and they both require scan-
ning the image in order to gain the pixel values. Thus, in
the encryption process, each round of the permutation-
diffusion operation requires at least twice scanning the
same image.
In this paper, we generate diffusion template using 3D
standard map and rotated image by using vertically and
horizontally red and green plane of the input image. We
then shuffle the red, green, and blue plane by using 3D
Figure 1. Permutation and diffusion based image crypto-
system.

K. GUPTA ET AL.
140
Cat map and standard map. Finally the Image is en-
crypted by performing XOR operation on the shuffled
image and diffusion template. The objectives of this new
design includes: 1) to efficiently extract good pseudo-
random sequences from a cascading of 3D cat and stan-
dard map for color image and 2) to simultaneously per-
form permutation and diffusion operations for fast en-
cryption.
The rest of this paper is organized as follows: Section
2 focuses on the efficient generation of pseudorandom
sequences. In Section 3, proposed algorithm is described
in detail. Section 4 presents simulation results and per-
formance analyses. In Section 5, conclusions and future
work.
2. Efficient Generation of Pseudorandom
Sequences
The generation of pseudorandom is based on two cas-
caded chaotic maps behave as a single chaotic map in
present case. The 3D cat map & 3D standard map are
taken for encryption. The pseudorandom matrix gener-
ated by this method is given below. (The explanation for
pseudorandom sequences generation is given in Section
3).
3. Proposed Algorithm
The proposed algorithm are divided into several stages
Table 1. Generation of pseudorandom values by proposed
method.
and explained below.
3.1. Diffusion Template
According to the proposal the diffusion template must
have the same size as main image. Let the main image
have m number of rows n number of columns then the
diffusion template is created as follows

255
, ,roundijk j
n






(1)
where 1im

, 1jn

 and . 13k
Equation (1) form the matrix with all rows filled with
linearly spaced number in between 0 to 255. The se-
quence is randomized by 3D standard map in discrete
form as given below.
The 3D standard map randomizes the pixels by real-
locating it in new position by utilizing its property of one
to one mapping. Figure 2 shows the final diffusion tem-
plate by using 3D standard map.


modiij m
 (2)
1sin mod
2


 
 



c
jjkKi pi n (3)
1 sin2sinmod
22
pp
kkK iKjp
pi pi

 
 
  

 

(4)
where the K1, K2 are the integers, p = 3 for the case of
color image and i′, j′, k′ shoes the transformed location of
i, j, k.


diff diff
,, ,,

I
ijkI ijk
 
.
3.2. Image Encryption
Step 1. The main image is divided into three separate
images IR, IG and IB as follows




,,
R,1
I
xyIxy

,,
G

,2
I
xyIxy

 
,,,3
B
I
xyIxy
where 1
x
m

 and 1
y
n.
Step 2. The Red and Green image are transform verti-
Figure 2. Diffusion template.

K. GUPTA ET AL. 141
cally and horilue image re-zontally respectively. The b
mains same and reconstructs the new image.

,m
2
RR
mod,
I
xy Ixmy

 





,m
2
GR
nod
I
xyIx yn



 


 
,,
BB
I
xyIxy


new ,,1 , R

I
xyI xy



new ,,2, G

I
xyI xy



new ,,3 , B

I
xyI xy

.
Step 3. Perform the first level confusion by usin2D
ca
w

where j′ and k′ are obtained by 2D cat map and p q are
erate Final confusion stage by two cascade
3D

g
t map. Slice the plane normal to R, G, B Planes by
I′new(i, j, k) = I′SRGB(j′, k′) = Inew(i, j, k)
here 1im , 1jn and 13k.
k
and

mo

dm

1modk n
xy
rrp


rpq
jj

y
kqj

integer > 0 and rx, ry are offset integer such that 0 ≤ rx ≤ m,
0 ≤ ry ≤ n.
Step 4. Gen
maps first by cat map then by standard map. So the
transformation of location (i, j, k) into (i″, j″, k″) is per-
formed by following equations.

1

 iaabiaj

mod




xzy z
yxzxyzy
aaaaaabkm



+
1mod
zxyxzyz zz

1
y
zxyzyzxz
yy
ibabaabbiab
jaa aaabbaa
abk n









1 m






xxy yx
xyxyxx yy
kabbbibj
aabbababk

modiik m
 



y
b


od

p
1sin mod
2
n
jijK in
pi


   
 




1sin 2
2sinmod
2
p
kkKipi
p
K
jp
pi

 







 





con ,, ,,
I
fi jkIijk
  

where
x
a,
y
a,
z
a,
x
b,
y
b,
z
b and 1
K
, 2
K
are
n step is followed by diffusion obtained
by
.3. Key Generation Process
he proposed method has a large number of variables
fling Ds = 8 bits.
8
ion template variables Dk1Dk2 = 8 + 8 =
16
. Sliced RGB plane Shuffling = Ss = 8 bits.
ts.
bi
p 7. Final Confusion shuffling Cs = 8 bits.
8 + 8 +
2
onfusion cat map variables CaCb = 8 + 8 =
16
0. Confusion offset of standard map Cx′Cy′Cz′
=
dard map variables Ck1Ck2 = 8
+
ructure
k1Dk2SsSxSySpSq
C
To
s.
.4. Image Decryption
tep 1. Generate the diffusion template in same way as
mation of location is done by two
ca
e re-transformation of location (i″, j″, k″) into (i, j,
k)
integers >0.
Each confusio
EXOR operations performed between each pixels of
Iconf and diffusion Idiff. The proposed image encryption
architecture is given in Figure 3.
= II I
encpconfdiff.
3
T
which can be used as key parameters but to avoid the
exceptionally large key and decreased key sensitivity, the
parameter which does not having great affects on en-
cryption are avoid or scaled. The selected key parameters
and their length are given below
Step 1. Diffusion template shuf
Step 2. Diffusion template offset value DxDyDz = 8 +
+ 2 = 18 bits.
Step 3. Diffus
bits.
Step 4
Step 5. Sliced RGB plane offset values SxSy = 8 bi
Step 6. Sliced RGB Plane Variables SpSq = 8 + 8 = 16
ts.
Ste
Step 8. Confusion offset of cat map CxCyCz =
= 18 bits.
Step 9. C
bits.
Step 1
8 + 8 + 2 = 18 bits.
Step 11. Confusion stan
8 = 16 bits.
Final key st
DsDxDyDzD
sCxCyCzCaCbCx’Cy’Cz’Ck1Ck2
tal bits = 8 + 18 + 16 + 8 + 8 +16 + 8
+ 16 + 16 + 18 + 16 = 148 bit
3
S
in encryption section.
Step 2. Re-transfor
scaded 3D maps firstly by standard map then by cat
map.
So th
is performed by following equations


modiik m

 

1sin mod
2
jijkin
pi
  
 
 



n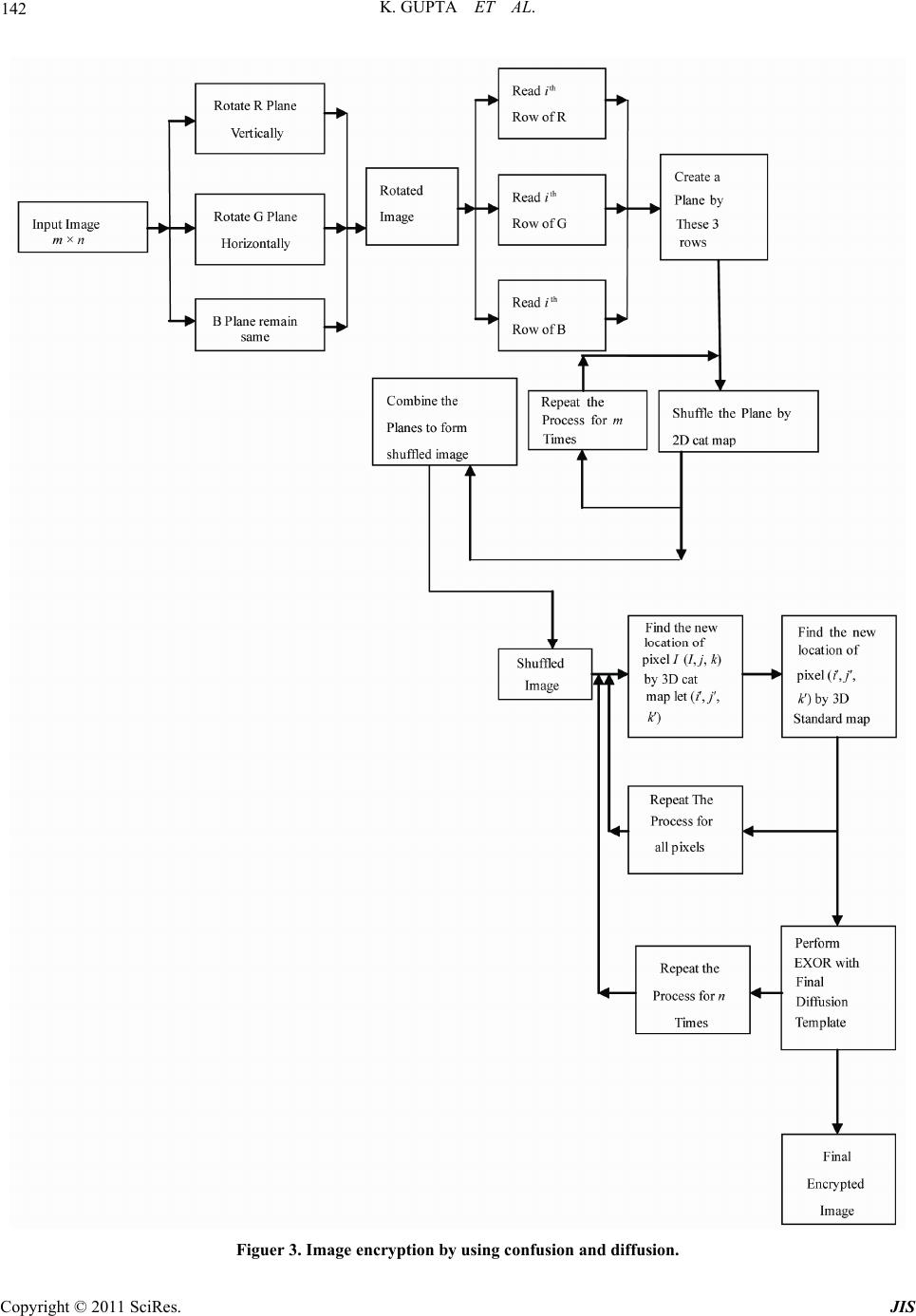



K. GUPTA ET AL.
142
Figuer 3. Image encryption by using confusion and diffusion.

K. GUPTA ET AL. 143
1sin2 mod
22
nn
kkkjk j
pi pi


 

 





1
mod

 





xzy z
yxzxyzy
iaabiaj
aaaaaab km




1
mod
zxyxzyz zz
p
y
zxyzyzxyy
x
ibabaabbiab
j aaaaabbaab
ak n




 





1mod
xxy yx
xyxyxxyy
kabbbibj
aabbababkp




 

Iretransf (i, j, k) = Iencp (i, j, k)
where
x
a,
y
a,
z
a,
x
b,
y
b,
z
b and , are
integers > 0.
Each confusion step is followed by diffusion obtained
by EXOR operations performed between each pixels of
Iretrnsf and diffusion Idiff
1K2K
dencp retrnsfdiff
I
II

.
Step 3. Performing inverse of First level confusion.
Slicing the plane normal to R, G, B Planes

,
 
SRGB dencp
,,
I
jkIijk


for each value of i, j changed from 0 to m, k changed
from 0 to 3.
De-shuffling the sliced plane
 
DRGB SRGB
,,
I
jk Ijk


where j′ and k′ are obtained by 2D cat map given below
m
n
where p and q are integers > 0, and rx, ry are offset inte-
gers such that 0 ≤ rx ≤ m and 0 ≤ ry ≤ n.
Recombining the planes for forming 3D matrix for next
operation


mod
xy
jjrrpk

 
1m
y
kqjrpq k od

 
DRGB
,, ,
I
ijk Ijk  .
Step 4. Re-rotating the image planes
Dividing main image into three separate images IR, IG
and IB as follows
 
,,
R

,1
I
xyIxy


 
,,
g

,2
I
xyIxy





,,,3
B
I
xy I xy

where 1
x
m and 1
y
n.
d plane verticallyScro lling the re

,m
2
RR
mod,
I
xy Ixmy







.
Scrolling the green plane horizontally

,m
2
GR
nod
I
xyIx yn









.
Blue plane remain intact.


,,
BB

I
xyIxy.
Step 5. Next recombination of planes are performed to
form final decrypted image




,,1 ,
final R
I
xyI xy



,,2,
final G
I
xyI xy


3 ,
B
,,
final
I
xyI xy
4. Performance Analysis
4.1. Key Space Analysis
The strong point of the proposed algorithm is the genera-
tion of the permutation sequence with the chaos se-
quence. The key space should also be suitably large to
make brute-force attack not feasible. In the proposed
algorithm, we use 148 bit key (37 Hex number) is used.
It has been observed in Figures 4(a) and (b) that with
slightly varying the initial condition of the chaotic se-
quence. It has been almost impossible to decrypt the im-
age.
4.2. Statistical Analysis
It is well known that passing the statistical analysis on
cipher-text is of crucial importance for a cryptosystem
actually, an ideal cipher should be strong against any
statistical attack. In order to prove the security of the
proposed image encryption scheme, the following Statis-
tical tests are performed.
4.2.1. Histogram Analysis
To prevent the access of information to attackers, it is
important to ensure that encrypted and original images
do not have any statistical similarities. The histogram
analysis clarifies that, how the pixel values of image are
distributed. A number of images are encrypted by the
encryption schemes under study and visual test is per-
formed.
An example is shown in Figure 5. In Figure 5 shows
histogram analysis on test image using proposed algo-
rithm. The histogram of original image contains great
sharp rises followed by sharp declines as shown in Fig-
ure 5 and the histograms of the encrypted images for
different round as shown in Figures 5(a)-(f) have uni-
form distribution which is significantly different from
original image and has no statistical similarity in ap-

K. GUPTA ET AL.
144
(a)
1010110D2833020202 and Decrypted by 0304002030402030-
03040020304020301011010110D2833040404 and Decrypted
(b)
Figure 4. (a) Input image encrypted with 0304002030402 030101
with
pe
tistical attack. The encrypted image histogram,
approximated by a uniform distribution, quite different
fr
very good correlaon among adjacent piels in
the digital image [3]. Equation (5) is used to study the
djacent pixels in horizontal,
1011010110D2833020203; (b) Input lenna image encrypted
by 03040020304020301011010110D2833040405.
arance. So, the surveyed algorithms do not provide any
clue for sta
is
om plain-image histogram.
4.2.2. Correlation Analysis
There is a ti x
Correlation between two a
vertical and diagonal orientations. This is shown in Fig-
ure 6.
x and y are intensity values of two neighboring pixels
in the image and N is the number of adjacent pixels se-
lected from the image to calculate the correlation. 1000
pairs of two adjacent pixels are selected randomly from
image to test correlation. The correlation coefficient be-


 
111
2
2
11
j
NN
j j
jj
NN
j
jj
x y
Ny y


 






(5)
2
2
11
j
N
jj
j
NN
j
jj
Nxy
Nx x









r
c

145 K. GUPTA ET AL.
(a)
(b)
(c)
(d)

K. GUPTA ET AL.
146
(e)
(f)
Figure 5. (a) Histogram for red, green and blue plane of original and encrypted image for R = 1; (b) Histogram for red, green
and blue plane of encrypted image for R = 2; (c) Histogram for red, green and blue plane of encrypted image for R = 4; (d)
Histogram for red, green and blue plane of encrypted image for R = 8; (e) Histogram for red, green and blue plane of en-
crypted image for R = 16; (f) Histogram for red, green and blue plane of encrypted image for R = 32.
Figure 6. Correlation for horizontal, vertical and diagonal.
tween original and cipher image is calculate in Table 6.
4.3. Key Space Analysis
Key space size is the total number of different keys that
can be used in the cryptography. Cryptosystem is totally
sensitive to all secret keys. A good encryption algorithm
should not only be sensitive to the cipher key, but also the
key space should be large enough to make brute-force at-
tack infeasible. The key space size for initial conditions and
control parameters is over than 2148. Apparently, the key
space is sufficient for reliable practical use.
4.4. Differential Analysis
In general, a desirable characteristic for an encrypted
image is being sensitive to the little changes in plain-
image (e.g. modifying only one pixel). Adversary can
create a small change in the input image to observe
changes in the result. By this method, the meaningful
relationship between original image and cipher image
can be found. If one little change in the plain-image can

K. GUPTA ET AL. 147
cause a significant change in the cipher-image, with re-
spect to diffusion and confusion, then the differential
attack actually loses its efficiency and becomes almost
useless. There are three common measures were used for
differential analysis: MAE, NPCR and UACI. Mean Ab-
solute Error (MAE). The bigger the MAE value, the bet-
ter the encryption security. NPCR means the Number of
Pixels Change Rate of encrypted image while one pixel
of plain-image is changed. UACI which is the Unified
Average Changing Intensity, measures the average in-
tensity of the differences between the plain-image and
Encrypted image.
Let C(i, j) and P(i, j) be the color level of the pixels at
the ith row and jth column of a W × H cipher and plain-
image, respectively. The MAE between these two images
is defined in
 
11
1
MAE, ,
WH
ji
cij pij
WH


 .
er two cipher-images, C1 and C2, wh
(6)
Consid ose cor-
responding plain-images have only one pixel difference.
The NPCR of these two images is defined in

,,
N
PCR 100%
ij
Dij
WH


 (7)
where W and H are the width and height of the image
and D(i, j) is defined as



 
0,if 1,2,
,.
1,if 1,2,





CijC ij
Dij CijCij

Another measure, UACI, is defined by the following
formula:

,
1, 2,
1
UACI 100%
255
ij
cijc ij
WH




. (8)
Tests have been performed on the encryption schemes
on a 256-level color image of size 256 × 256 shown in
Figures 5(a)-(f). The MAE, NPCR and UACI experi-
ment result is shown in Tables 4 and 2. The Tables 3
and 5 compare the result of Yo
based on chaotic map and our. Results obtained from
to
ttle changes in the input image is under 0.01%. Ac-
ation result, the rate influ-
nce due to one pixel change is very low. The results
demonstrate that a swiftly change in the original image
will result in a negligible change in the ciphered image.
4.5. Information Entropy Analysis
It is well known that the entropy H(m) of a message
source m can be measured by
ng previous related work
NPCR show that the encryption scheme’s sensitivity
li
cording to the UACI estim
e
  
1
0
1
log
m
i
ii
Hmpm pm


 (9
where M is the total number of symbols mi ∈ m; p(mi)
represents the probability of occurrence of symbol mi
and log denotes the base 2 logarithm so that the entropy
is expressed in bits. For a random source emitting 256
symbols, its entropy is H(m) = 8 bits. This means that the
cipher-images are close to a random source and the pro-
posed algorithm is secure against the entropy attack. The
test result on different image for different round is de-
fined in Table 7.
4.6. Speed Analysis
cesses. In general, en-
cryption speed is highly dependent on the CPU/MPU
structure, RAM size, Operating System platform, the
programming language and also on the compiler options.
So, it is senseless to compare the encryption speeds of
two ciphers image.
Without using the same developing atmosphere and
optimization techniques. Inspire of the mentioned diffi-
culty, in order to show the effectiveness of the proposed
image encryption scheme over existing algorithms. We
Table 2. NPCR, UACI and Entropy for key sensitivity test.
Lenna Error
Image R = 2 R = 3 R = 4
)
Apart from the security consideration, some other issues
on image encryption are also important. This includes the
encryption speed for real-time pro
NPCR 99.5966593424998836263 99.651082356 .609
UACI 52.539481368751.6816741344 50.603535970
Entropy 7.999130689807.99912231127 7.9991865161
NPCR 99.610392252699.5905558268 99.599711100
8581327550 48.719709807
Entropy 7.999010789687.99905756543 7.9991734549
Baboon Error Image
UACI 46.999834846047.
Table 3. Comparison of NPCR
Name of image R = 1
and UACI with Yong Wong et al.
R = 2 R = 3
Our Yong Wang et. alOur Yong Wang et. alOur Yong Wang et al.
NPCR 99.62 97.621
Airplane
UACI 33.19 32.909
99.60 99.637 99.62 99.634
33.10 33.575 33.35 33.580

K. GUPTA ET AL.
148
eren
= 4 R = 8 R = 10 R = 16 R = 32
Table 4. NPCR and UACI for diff
Image R = 1 R = 2 R = 3
t round on different color image.
R
NPCR 99.55 99.57 99.59 99.59 99.61 99.60 99.60 99.61
Baboon
UACI 37.17 38.68 39.00
MAE 71.65 74.52 75.29
NPCR 99.63 99.64 99.59
Lenna
UACI 28.87 27.51 27.33
38.78 38.69 38.88 39.03 38.89
75.18 75.23 75.37 75.34 75.50
99.62 99.62 99.61 99.62
UACI 38.05 38.26 37.99
MAE 75.20 74.68
99.61 99.59 99.60
33.28 33.32 33.31
99.59
27.42 27.43 27.64 27.51 27.37
77.58 77.76 77.84 77.67 77.54
99.58 99.63 99.62 99.62 99.62
38.03 38.34 38.20 38.33 38.11
74.48 74.89 74.62 74.62 74.61
9.62 99.63
MAE 80.84 77.24 77.46
NPCR 99.62 99.62 99.58
Pepper
74.27
NPCR 99.62 99.60 99.59
Airplane
33.35
9
UACI 33.19 33.10 33.27 33.329
Table 5. The round number of scanning-imag
tion and diffusion to achieve NPCR > 0.996 a
NPCR UACI
No. of Round for Confusion
and Diffusion
e, permuta-
nd UACI >
0.287.
Our >0.996 >0.287 1
Ref. [3] >0.996 >0.333 2
Ref. [4] >0.996 >0.333 18
Ref. [5] >0.996 5
Ref. [6] >0.996 >0.333 6
Ref. [7] >0.996 >0.333 6
evaluated the performance of encryption schemes with
an un-optimized MATLAB 7.0 code. Performance was
measured on a machine with Intel core 2 Duo 2.00 GHz
CPU with 2 GB of RAM running on Windows XP. The
time for encryption and decryption is measured for dif-
ferent round is shown in Tables 8 and 9.
4.7. FIPS 140 Testing
We also sr proposed algorithm pass the FIPS
14ss testsThere are four tesono-bit,
Poker, Runs tests and Lng run tesach
was to test the randomness of a sam-
quence length of 20,0 as follo
how that ou
0-2 randomne. ts: M
ots. E of the tests
designedple se
00 bitsws:
4.7.1. The Monobit Test
1) Calculate x which is the number of ones in the
20,000 bit stream.
2) The test is passed if 9725 < x < 10,275.
4.7.2. The Poker Test
1) Divide the 20,000 bit stream into 5000 contiguous 4
bit segments. Count and store the number of occurrences
of each of the 16 possible 4 bit values. Denote g(i) as the
number of each 4 bit value i where 0 - 15.
2) Calculate x by

15 2
0
5000
5000 i
Xgi


 (10)
16
t is if 2.16 < 6.17.
4.7e R
un mc-
tivf aeenf
all lengths in the sld be counted and
sto
teifof runs is each
cind e
.
4.7.4. The Lg Run Test
1) Findngest run in the 20,000
e ngen in f
20bothnd z smaller , the
test is passed.
3) The tespassedx < 4
.3. Thuns Test
1) A rrepresents a aximal sequene of consecu
e bits oll ones or all zros. The incidces of runs o
ample stream shou
red.
2) Thest is passed the number
w
10
ithin theorresponding terval specifie below Tabl
on
the lobits.
2) If th length of the lost ruthe bit stream o
,000 bit ( of one aero) isthan 26

K. GUPTA ET AL. 149
Correlation coefof plae orrelatiicient ofimage
Table 6. Correlation coefficient for plain and cipher image.
ficient in imagCon coeff Cipher
Images Horizontal Vertical Diagonal Horizontal Vertical Diagonal
Baboon 8646 0.810.007 0.
.9156 0.8603 0.006 0.091
Pepper 0.9376 0.890.006 0.
0.0.829314 0.004 037
Lena 00.8808
0.9364
0.001
0.005 35 023
Table 7. Entropy test for different color image.
Im R = 1 R = 2 R = 3 R = 4 R = 8 R = 10 R = 16 R = 32 Yong Wang et al. [7]age
Our Scheme
Baboon 7.9988 7.9990 7.9991 7.9992 7.9990 7.9990 7.9990 7.9991 -
Lenna 7.9981 7.9991 7.9991 7.9992 7.9991 7.9990 7.9990 7.9990 7.9990
Pepper 7.9987 7.9991 7.9991 7.9989 7.9989 7.9992 7.9992 7.9992 7.9990
Air7.9989 7.9989 7.9991 7.9991 7.9991 7.9991 7.9991 7.9992
Boat 7.9986 7.9992 7.9991 7.9990 7.9990 7.9990 7.9991 7.9991
plan -
-
Table 8.ptioin seor difround.
Image R3 R = 4 R =R =R
Encryn time cond fferent
= 1 R = 2 R = 8 10 = 16 R = 32
Our Scheme
Baboon 0.510 0.87 1.20 1.56 2.94 3.65 5.73 11.24
5615.697 11.225
per 0.521 0.87 1.197 1.561
Airplan 0.521 0.87 1.197 1.561 11.225
Bat 21 0.81.5615.697 11.225
Lenna 0.521 0.87 1.197 1.
Pep
2.933 3.662
2.933 3.662 5.697 11.225
2.933 3.662 5.697
o0.57 1.197 2.933 3.662
Table 9. Deption time in se
Im× 25 = 1 R = 2 R =
crycond for different round.
4 R = 8 R = 10 R = 16 R = 32 age 256 6 R R = 3
Our Scheme
Baboon .43 0.77 1.12 1.470 2.85 3.55 5.62 11.17
429 0.77 137 1.471 2.869 3.548 5.618
r 430 0.78 139 1.472 2.11.22
Airplan 0.429 0.77 1.137 1.471 2.11.20
41.523 5.594 11.15
0
Lenna0.1.11.20
Peppe0.1.869 3.549 5.619
869 3.548 5.618
Boat 0.434 0.722 1.065 1.4 2.807 3
We need to change the testing algorithm to suit to im-
age data so we randomly chose 100 streams of 20,000
consecutive bits from the ciphered images of image A.
Then we find statistics of the randomly chosen 100
reams for each test and compared them to the accep-
ow the numbers of the samples
mong 100 randomly chosen samples, which passed the
places the tradi-
better encryption using cascading of 3D standard
an
orizontally red and green plane of the input image.
e then shuffle the red, green, and blue plane by using
ap. Finally the Image is en-
crthe shuffled
im
ut, both confirming that the new cipher
st
tance ranges. Table 11 sh
a
Mono-bit, Poker, Long run tests and run tests.
5. Conclusions
This paper presents a technique which re
tional preprocessing complex system and utilizes the
basic operations like confusion, diffusion which provide
same or
d 3D cat map. We generate diffusion template using
3D standard map and rotate image by using vertically
and h
W
3D Cat map and standard m
ypted by performing XOR operation on
age and diffusion template. Completion of the design,
both theoretical analyses and experimental tests have
een carried ob

K. GUPTA ET AL.
150
Length of the run 3 ≥6
Table 10. FIPS-140 test range.
1 2 4 5
Reerval 5 86 3 1quired int2315 - 2681114 - 13527 - 72240 - 384 03 - 209 103 - 209
Table 11. FIPS-140 pass, F = f
Name of image R = 1 R = 2 R = 3 R = 4 R = 8 R = 10 R = 16 R = 32
test P =ail.
runs 10P, 10P 12P, 12P 16P, 12P 17P, 14P 11P, 12P 13P, 15P 12P, 14P 15P, 11P
pocke
mono 1008
r 374.4P 3P 13.644P 678P 556P
1P 9913P
P , 12P , 13PP, 20P P, 12P
P 0P 856P1.558P 2P
P P 38P 054P 900P 2P
P 3P , 13P , 13PP, 11P P, 14P
P 7P 454P0.227P .929P r
mono 10085P 9982P 10001P 9967P 10048P 9994P 9913P 10036P
runs 12P, 10P 5P, 12P 12P, 13P 12P, 11P
pocker 880.25F 30.016P 13.504P 12.134P 16.761P 20.108P 12.800P 9.568P Airplan
m10030P 10075P9975P 40P 1P P
7F
2P
9.894
9975P
15.44 12.985P
9952P
8.12.12.556P
2P
Baboon
9969P
5P
9990P 10031003
runs 10P, 11P13P, 1513P, 117P, 13P12P13P 1512
pocker 317.4F 24.30P14.0228.99218.227P 21. 118.75
Lenna
mono 9956P 10025P10103996799 1091011
runs 12P, 16P13P, 1512P, 112P, 14P12P13P 1314
pocker138.41F 13.196P12.05713.3318.227P 20. 127Peppe
14P, 13P 17P, 23P 12P, 14P 14P, 13P 1
ono 9996P99100799469973P
poshigh sy and fast encryptioeed. In
conclusion, therefore, the new cipher indeed has excel-
lent potential for practical imagption applications.
6. References
[1] hen, Y. d C. K., “A Syc Image
Encryption Scheme Based on 3D Chaotic Cat Maps,”
Chaos Solitons & Fractals, Vol. 21
[4] Z. ang and W. Guan, “Chaos-Based Image
Encrrithm,” Physics Letters A, Vol. .
1-3. 153
sesses ecuritn sp
e encry
G. CMao an Chuimmetri
, No. 3, 2004, pp.
749-761. doi:10.1016/j.chaos.2003.12.022
[2] D. Xiao, X
Guan, F. Hu
yption Algo346, No
, 2005, pp-157.
doi:10.1016/j.physleta.2005.08.006
S. Lian, J. Sun and Z. Wang, “A Cipher Based on a
Suise of thotic Staap,” C oli-
tons & Fractals, Vol. 26, No. 1, 2005, pp. 117-129.
[5] Block
table Ue Chandard Mhaos S
doi:10.1016/j.chaos.2004.11.096
[6] K. W. Wong, B. S. Kwok and W. S. Law, “A Fast Image
ased on Chaotic Standard Map,”
Physics Letters A, Vol. 372, No. 15, 2008, pp. 2645-2652.
Encryption Scheme B
. LiaP. Wei, “Analysis andvement
of a Chaos-Based Image Encryption Algorithm,” Chaos
Solitons & Fractals, Vol. 40, No. 5, December 2007.
[3] ga, K.-Wong, X. Fo and G.en, “A
haos-Bast Imacryptionrithm,”
o ng, Vol. 12.
o and Impro
Y. Wan. W. Lia R. Ch
New Cased Fge En Algo
Applied Soft Cmputi1, No. 1, 2011, pp. 514-52
doi:10.
doi:10.1016/j.phy07.12.0sleta.20 26
[7] Y. Mao, G. Chen and S. Lian, “A Novel Fast Image En-
crypcheme B 3D C Baker Maps,” In-
ternational Journal of Bifurcation and Chaos, Vol. 14,
No. 10, 2004, pp. 3613-3624.
tion Sased onhaotic
doi:10.1142/S0218 40115112740X
1016/j.asoc.2009.12.011