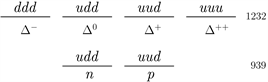Open Access Library Journal
Vol.04 No.12(2017), Article ID:81065,10 pages
10.4236/oalib.1104164
On the Significance of Standard Model Errors
Eliahu Comay
Charactell Ltd., Tel-Aviv, Israel
Copyright © 2017 by author and Open Access Library Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 16, 2017; Accepted: December 11, 2017; Published: December 14, 2017
ABSTRACT
The paper discusses the existence of errors in the Standard Model. An adequate amount of examples and references support the arguments. The errors belong to the electromagnetic, strong and weak interactions sectors of the Standard Model. It turns out that this state of affairs is far from being well-known and too many people unjustifiably glorify the Standard Model as an excellent theory. It is explained why a reexamination of the Standard Model can only improve the status of physics.
Subject Areas:
Theoretical Physics
Keywords:
The Standard Model, Electrodynamics, Strong Interactions, Weak Interactions, Error Correction

1. Introduction
Error correction is widely recognized as an extremely important assignment of human activity. Factories call it QA, computer programmers call it debugging, etc. The concept named Devil’s Advocate [1] is relevant to this issue, because it presents objections to mainstream ideas and in so doing it encourages a deeper examination of these ideas. As a matter of fact, the task of error correction require a preliminary step where specific errors are identified.
Evidently, this issue is an important aspect of the scientific activity in general. The present work examines error correction within the realm of physics. Here errors (or error candidates) are identified as mathematical inconsistencies of a given theoretical structure or as experimental data that cannot be explained by mainstream theories of the relevant epoch. The following lines describe briefly two actual periods that illustrate this topic.
William Thomson (Lord Kelvin) was a leading physicist during the latter decades of the 19th century. At this time classical non-relativistic physics was recognized as the mainstream physical theory. In a famous talk delivered at about year 1900 he pointed out two dark clouds that lie over physics: the puzzling result of the Michelson-Morley experiment and the problem of black body radiation [2] . The identification of these problems has certainly en- couraged people to think about them and to try finding how they can be settled.
At about the same time M. Planck has introduced the quantum concept as an element of his explanation of black body radiation data [3] . Plank’s work was the first step towards the creation of quantum theories.
The solutions of the two problems formulated by Kelvin have made a very far reaching impact. It has turned out that “two major physical theories were developed during the twentieth century starting from these issues: for the former, the theory of relativity; for the second, quantum mechanics. Albert Einstein, in 1905, published the so-called “Annus Mirabilis papers”, one of which explained the photoelectric effect and was a precursor of quantum mechanics, another of which described special relativity” [2] .
The developments indicate that the 19th century physical theories have not been abandon completely. As a matter of fact, these theories are quite good for cases where the particles’ speed is much smaller than the speed of light and if the classical limit of quantum mechanics holds.
The 1920s is another interesting epoch in the development of physical theories. At the beginning of this decade the Bohr atomic model was regarded as a promising approach because it provides a good description of the hydrogen atom energy levels [4] . However, attempts to extend this theory in order to explain atoms having more than one electron have ended in vain (see e.g. [5] , p. 2).
The first step has been taken by L. de Broglie who described in 1924 the wave nature of a massive particle. Few years later Heisenberg and Schroedinger have formulated quantum mechanics. In this case, the Bohr atomic theory has been abandoned completely (except in some popular and nonscientific illustrations of atomic structure).
The previous examples show two periods-the first decade of the twentieth century and the 1920s-where the mainstream physical community discussed scientific contradictions and abandoned useless theories. In particular, Bohr himself has abandoned his atomic theory and participated in the development of the present form of quantum mechanics. The behavior of the physical community in these periods contributes to the great scientific legacy of seeking better theories. This activity relied on the effect of error recognition which was a great stimulus for the search for a way out from the contradictions. The main objective of the present work is to show that, unfortunately, the present state of affairs is different. In particular, the Standard Model (SM) takes a primary status in presently accepted particle physics theories. The paper points out many SM errors and discusses the attitude of the current physical community to these errors.
Units where are used. Greek indices run from 0 to 3. The metric is diag. (1, −1, −1, −1). Relativistic expressions are written in the standard notation. Square brackets [ ] denote the dimension of the enclosed expression. In a system of units where there is just one dimension, and the dimension of length, denoted by [L], is used. In particular, energy and momentum take the dimension [L−1] and the electric charge is a dimensionless pure number. The second section presents quite a few SM specific errors. The third section discusses the rather strange effect where many people support the SM. The last section contains concluding remarks.
2. Examples of Standard Model Errors
This section is dedicated to a description of quite a few SM errors that have been piled up during many decades. These errors substantiate the claim stating that the present physical community has serious problems. Each error is briefly explained and an adequate amount of references support them. The references also contain other SM contradiction that are not explicitly mentioned in this work.
1) Believe it or not, a free gauge transformation is unacceptable in electro- magnetic theories based on the variational principle in general and in QED in particular. The correct form of the relevant theorem is: “If a Lagrangian function is invariant under a transformation and both the Lagrangian function and the transformation are mathematically consistent then∙∙∙”. Evidently, mathematical consistency is a crucial requirement that every physical theory must satisfy. The following arguments explain the root of the error of electromagnetic gauge transformations.
The Lagrangian density is the primary element of electrodynamics that is based on the variational principle. Here the charge-fields interaction term is (see [6] , p. 78)
(1)
where is the charge’s 4-current and is the 4-potential. The electro- magnetic 4-potential of a charge e takes the form of the Lienard-Wiechert formula (see [6] , p. 174 or [7] , p. 656)
(2)
Here denotes the 4-vector from the retarded space-time position of the charge to the field point and is the retarded 4-velocity of the charge.
By definition, the gauge 4-potential is derived from an arbitrary function of the four space-time coordinates (see [8] , p. 342 after (8.1.13); [9] , p. 482, after (15.1); [10] , p. 207 after (23b); [11] , p. 192; [12] , p. 316, after (14.21)). Let
(3)
be the gauge quantity obtained from . Evidently, of (2) is a 4-vector whose dimension is [L−1]. Therefore, dimension and relativistic covariance of physical expressions mean that also the additional gauge 4-vector of (3) must be a 4-vector whose dimension is [L−1]. In principle, these restrictions are violated by an ordinary gauge transformations which is an arbitrary function of the four space-time coordinates. More gauge contradictions are discussed in [13] . In particular, this article shows a specific example which proves that a gauge transformation is inconsistent with a simple interference calculation.
2) The present form of the electromagnetic fields term of the QED Lagrangian density is (see [8] , p. 349)
(4)
Here the electromagnetic fields tensor is the sum of bound fields and radiation fields
(5)
Now, radiation fields have spin = 1 and an odd parity (see the photon data in [14] ). On the other hand, one can regard the hydrogen atom as a measuring device. An examination of the hydrogen atom ground state proves that bound fields have spin = 0 and an even parity. Hence, the introduction of (5) into (4) boils down to
(6)
Evidently, the last term of (6) has an odd parity while other terms have an even parity. It means that the present form of the QED Lagrangian density violates parity conservation whereas electrodynamics conserve parity. Furthermore, the angular momentum of the product of the spin = 0 and the spin = 1 functions of the last term of (6) is unity. By contrast, the Lagrangian density of a physical field should be a Lorentz scalar. For these reasons, the Lagrangian density (4) is certainly an erroneous element of the present structure of QED. For further details see [15] and references therein.
3) The recent QED failure to explain the proton’s charge radius data (see [16] as well as the two different values of the proton charge radius in [14] ) provides an experimental support for the theoretical QED contradictions mentioned above.
4) The following lines prove that the SM strong interactions sector (QCD) has been constructed on an erroneous basis. For this end, let us examine the four baryons. In an attempt to prove the need for QCD, particle physics textbooks state that the single particle wave functions of the three uuu quarks of the baryon are symmetric ground state s-waves. Thus, the isospin quantum number of the baryon is a symmetric isospin state and its space-spin and parity state is a symmetric space-spin state. Hence, the books claim that these data demonstrate a fiasco of the Fermi-Dirac statistics of ordinary quantum mechanics (see [17] , p. 5), because the three uuu quarks are fermions and their wave function must be antisymmetric. An analogous argument has also been used by one of the QCD pioneers, who refers to the three sss quarks of the baryon [18] . The following lines prove that the quantum state of the and of the baryons is not a symmetric single particle s-wave.
Figure 1 illustrates energy levels of the two nucleons and those of the four baryons. The goodness of the isospin notion indicates that all the baryons have the same space, spin and isospin symmetry (for reading a proof of this claim, see [19] , p. 57). Hence, if the state of the baryon is inconsistent with fundamental laws of ordinary quantum mechanics then the same is true for the state of the and the baryons. However, it is clearly seen in Figure 1 that the and the baryons are excited states of the neutron and the proton, respectively. As excited states, the laws of ordinary quantum mechanics prove that the and the baryons should have excited space-spin states. This conclusion holds for every member of the isospin quartet of Figure 1. Hence, the single particle spatial part of the quarks is not a ground state s-wave and its entire state is consistent with the laws of ordinary quantum mechanics.
An analogous argument holds for the baryon. Here the octet and the decuplet representations of the SU(3) group respectively replace the doublet and the quartet representations of the SU(2) isospin group of Figure 1 (see [20] , pp. 147, 152).
It can be concluded that contrary to the argument used for the need of QCD, the state of the and of the baryons is not a single particle s-wave.
5) Experiment shows that the cross-section of a hard photon scattered on a proton is about the same as the corresponding neutron data [21] . This effect belongs to the combined domains of electromagnetic and strong interactions. The SM has no explanation for this effect [22] . The following issue is relevant to this matter. The photon is an elementary particle which is known for more than 100 years and the nucleons are the best-known hadrons. However, many particle physics textbooks do not contain an appropriate discussion of hard photon-nucleon interaction in general and of the above mentioned proton-neutron similarity in particular.
Figure 1. Baryonic energy levels of doublet and quartet isospin states, and the quarks that compose each of them (see text).
6) QCD is inconsistent with many experimental data [23] . One can also read a popular science book that discusses many aspects of this issue [24] . Items 7, 8 describe two examples of these QCD errors.
7) The EMC effect is known for more than 30 years. The data prove that the self-volume of quarks increases with the increase of the number of nucleons in nuclei. It turns out that QCD predictions are completely inconsistent with this effect [25] . This QCD problem has not been settled yet. Indeed, on April 14, 2017 the Wikipedia item of the EMC effect describes it in the following words: “The EMC effect has been bewildering physicists up to the present day” [26] . Similarly, a recent CERN publication admits that the data still puzzles QCD supporters [27] .
8) Experimental data show that the proton radius is larger than that of the pion [14] . Another proton information says that its quarks are enclosed in a volume that is much smaller than that of its antiquarks. (This information is derived from the uncertainty principle and the width of the momentum graphs of the proton’s quark and its antiquark (see [20] , p. 281)). QCD has no explanation for the effect where the pion’s one quark can hold the antiquark within a rather small volume whereas the proton’s four quarks (the three valence quarks and the antiquark’s companion) cannot hold the antiquark within a volume which is at least not larger than their own volume.
9) The electroweak theory of the SM contains erroneous elements (see Section 2 in [28] ). For example, the are two electrically charged particles which the electroweak theory regards as elementary. These particles play a crucial role in this theory. However, in spite of the fact that the electroweak theory is about 50 years old, this interpretation of the contradicts Maxwellian electrody- namics because it does not satisfy charge conservation [28] . The following evidence illustrates this issue. In the case of the electron, the Dirac theory provides an expression for a conserved 4-current (see [29] , p. 24). By contrast, the electroweak theory is nearly 50 years old. However, people working with the CERN LHC machine still use an effective expression for the electromag- netic interactions (see e.g. Equation (3) in [30] ).
10) The SM electroweak theory is inconsistent with the data. For example, Equation (21.3.2) of [31] , p. 305 means that the electroweak theory treats the neutrino as a massless two-component spinor. By contrast, it is now recognized that the neutrino is a massive four-component spinor [32] . Referring to this issue, one should note that Wigner’s analysis of the representations of the inhomogeneous Lorentz group (see [33] ; [34] , pp. 44-53; [35] , pp. 143-150) proves that a massive particle and a massless particle are inherently different physical objects.
11) A mathematically real quantum function cannot describe an elementary massive particle. This assertion is proved in [36] . It follows that the Majorana neutrino theory, the Yukawa theory of the nuclear force, the electroweak Z theory, and the mathematically real Higgs boson theory are wrong.
This section presents a quite long list of SM errors which are still awaiting settlement. Several aspects of these SM errors are discussed below.
3. Discussion
The SM aims to formulate the physical laws of three kinds of interactions: electromagnetic. strong and weak. Each of these interactions is addressed by appropriate items of the foregoing list, which present well documented specific errors. Therefore, the SM contains theoretical and experimental errors that are relevant to all forces claimed to be covered by this theory. More examples of SM errors can be shown.
It turns out that contrary to what is expected from a scientific community, SM proponents simply ignore this predicament and tell people that the SM is free of any contradictions. As a matter of fact, some of them go even further and use groundless superlatives in their description of the SM. One can find many statements of this kind in the literature and on the web. Here are few examples of SM glorification that have been published in the new millennium by institutes and individuals. These examples indicate that even persons who do not belong to the present establishment unjustifiably adhere to the SM.
1) Fermilab is a large USA national laboratory. On November 18, 2011 it declared: “The Standard Model: The most successful theory ever” [37] . Fermilab repeated this groundless declaration on December 18, 2016 [38] .
2) CERN is a very large European research center. An official CERN publication declares: “everything we know up to now is described by the Standard Model” [39] . It is quite strange to realize that this baseless declaration contradicts another CERN publication entitled “The EMC effect still puzzles after 30 years” [27] .
3) In the introduction to his book [40] , R. Oerter praises the SM, and like the above mentioned Fermilab declaration, he belittles the merits of other scientific theories. Thus, he refers to the SM and states: It surpasses in precision, in universality, in its range of applicability from the very small to the astronomically large, every scientific theory that has ever existed. This theory bears the unassuming name “The Standard Model of Elementary Particles”.
4) M. Strassler completely ignores the above mentioned SM errors and states in [41] :
SM is simplest and most elegant theory consistent with data:
• Completely self-contained; no missing parts, no inconsistencies
• No confirmed conflicts with any existing experiments!
• Simplest and most elegant → the one most likely to be right
5) P. Woit is certainly a physicist who is not afraid to express a critical opinion on current trends of mainstream physical research [42] . Unfortunately, he himself adheres to the fundamentally erroneous opinion of SM glorification. For example, in the above mention book he declares: “The standard model has been such an overwhelming success that elementary particle physics is now in the historically unparalleled situation of having no experimental phenomena to study that are in disagreement with the model. Every particle physics experiment that anyone has been able to conceive and carry out has given results in precise agreement with the standard model.” (see the top of p. 91 in [42] ). It turns out that he has not changed his mind and on June 24, 2015 he published the following statements: “∙∙∙one remarkable aspect of the Standard Model is that it is consistent all the way up to much higher energies than we have any hope of probing experimentally. One can take the theory’s consistency with all current data as evidence that the Standard Model may be something rather close to a final theory” [43] . Beside the inconsistency of his statements with the data described in Section 2, readers may also wonder how can he be sure that the SM is consistent at energies so high that no experiment has ever reached?
6) The physical approach of L. Smolin is analogous to that of P. Woit. Indeed, in the same year each of them published a book that criticizes the popular idea of string theory [42] [44] . Unfortunately, like P. Woit, he praises the SM. For example, in the introduction to his book he refers to the period that begins with the SM construction. Here he defies evidence and declares: “No one has since done an experiment that was not consistent with this model∙∙∙”.
The above mentioned list of SM glorification is just a drop in the ocean. Indeed, one can use modern search utilities an find many other SM supporting statements in the scientific literature.
4. Concluding Remarks
The SM validity is examined in this work. The second section deals with many examples indicating that this theory is incompatible with well-established experimental data as well as with mathematical consistency. The third section presents quite a few quotes showing that in spite of these contradictions, too many people are unaware of the actual situation and groundlessly glorify the SM as a very successful and contradiction-free theory.
The order of the problematic items of the second section groups together issues that belong to a specific force-electromagnetic, strong and weak. Taking a scientific point of view, each erroneous item is equally important because science cannot proceed further without the confidence that it relies on an error-free basis.
The main purpose of this work is to convince readers that the present state of affairs requires a further examination of the SM validity as a physical theory. Therefore, it aims to stimulate members of the physical community to carry out a closer examination of the issues presented in the second section. Nothing bad can come out of this assignment. Indeed, if the SM is a really good theory then people will better understand some new aspects of its structure. On the other hand, even if only a few of the contradictions mentioned above are valid, then the SM should either be corrected or discarded. Evidently, changes in the SM may affect other physical fields, like cosmology.
Cite this paper
Comay, E. (2017) On the Significance of Standard Model Errors. Open Access Library Journal, 4: e4164. https://doi.org/10.4236/oalib.1104164
References
- 1. https://en.wikipedia.org/wiki/Devil
- 2. https://en.wikipedia.org/wiki/William_Thomson,_1st_Baron_Kelvin
- 3. https://en.wikipedia.org/wiki/Max_Planck
- 4. https://en.wikipedia.org/wiki/Niels_Bohr
- 5. Dirac, P.A.M. (1978) Mathematical Foundations of Quantum Theory. In: Marlow, A.R., Ed., Academic Press, New York.
https://doi.org/10.1016/B978-0-12-473250-6.50005-4 - 6. Landau, L.D. and Lifshitz, E.M. (2005) The Classical Theory of Fields. Elsevier, Amsterdam.
- 7. Jackson, J.D. (1975) Classical Electrodynamics. John Wiley, New York.
- 8. Weinberg, S. (1995) The Quantum Theory of Fields. Vol. I, Cambridge University Press, Cambridge.
- 9. Peskin, M.E. and Schroeder, D.V. (1995) An Introduction to Quantum Field Theory. Addison-Wesley, Reading Mass.
- 10. Pauli, W. (1941) Relativistic Field Theories of Elementary Particles. Reviews of Modern Physics, 13, 203.
https://doi.org/10.1103/RevModPhys.13.203 - 11. Yang, C.N. and Mills, R. (1954) Conservation of Isotopic Spin and Isotopic Gauge Invariance. Physical Review, 96, 191.
https://doi.org/10.1103/PhysRev.96.191 - 12. Halzen, F. and Martin, A.D. (1984) Quarks and Leptons, an Introductory Course in Modern Particle Physics. John Wiley, New York.
- 13. Comay, E. (2017) Gauge Contradictions in the QED Lagrangian Density. OALib Journal, 4, e3596.
http://www.scirp.org/journal/PaperInformation.aspx?PaperID=76182 - 14. Patrignani, C. et al. (Particle Data Group) (2016) Review of Particle Physics. Chinese Physics C, 40, 100001.
http://pdg.lbl.gov/ - 15. Comay, E. (2015) Interrelations between Mathematics and Experiment in the Present Structure of Quantum Electrodynamics. OALib Journal, 2, e2211.
http://www.scirp.org/Journal/PaperInformation.aspx?PaperID=69004 - 16. Pohl, R., et al. (2010) The Size of the Proton. Nature, 466, 213-216.
https://doi.org/10.1038/nature09250 - 17. Halzen, F. and Martin, A.D. (1984) Quarks and Leptons. Wiley, New York.
- 18. Fritzsch, H. (2012) CERN Courier.
http://cerncourier.com/cws/article/cern/50796 - 19. Comay, E. (2011) Spin, Isospin and Strong Interaction Dynamics. Progress in Physics, 4, 55.
- 20. Perkins, D.H. (1987) Introduction to High Energy Physics. Addison-Wesley, Menlo Park.
- 21. Bauer, T.H., Spital, R.D., Yennie, D.R. and Pipkin, F.M. (1978) The Hadronic Properties of the Photon in High-Energy Interactions. Reviews of Modern Physics, 50, 261.
- 22. Comay, E. (2003) Remarks on Photon-Hadron Interactions. Apeiron, 10, 87.
- 23. Comay, E. (2012) The Regular Charge-Monopole Theory and Strong Interactions. Electronic Journal of Theoretical Physics, 9, 93.
- 24. Comay, O. (2014) Science or Fiction? The Phony Side of Particle Physics. S. Wachtman’s Sons.
- 25. Aubert, J.J., et al. (1983) The Ratio of the Nucleon Structure Functions F2N for Iron and Deuterium. Physics Letters B, 123, 275-278.
https://doi.org/10.1016/0370-2693(83)90437-9 - 26. EMC Effect.
https://en.wikipedia.org/wiki/EMC_effect - 27. CERN Courier (2013) The EMC Effect Still Puzzles after 30 Years.
http://cerncourier.com/cws/article/cern/53091 - 28. Comay, E. (2016) A Theory of Weak Interaction Dynamics. OALib Journal, 3, 1-10.
http://www.scirp.org/journal/PaperInformation.aspx?paperID=72788 - 29. Bjorken, J.D. and Drell, S.D. (1964) Relativistic Quantum Mechanics. McGraw-Hill, New York.
- 30. Aad, G., et al. (2012) Measurement of the WW Cross Section in s = 7 TeV pp Collisions with the ATLAS Detector and Limits on Anomalous Gauge Couplings. Physics Letters B, 712, 289-308.
https://doi.org/10.1016/j.physletb.2012.05.003 - 31. Weinberg, S. (1995) The Quantum Theory of Fields, Vol. 2. Cambridge University Press, Cambridge.
- 32. Formaggio, J.A. and Zeller, G.P. (2012) From eV to EeV: Neutrino Cross Sections across Energy Scales. Reviews of Modern Physics, 84, 1307.
https://doi.org/10.1103/RevModPhys.84.1307 - 33. Wigner, E. (1939) On Unitary Representations of the Inhomogeneous Lorentz Group. Annals of Mathematics, 40, 149-204.
https://doi.org/10.2307/1968551 - 34. Schweber, S.S. (1964) An Introduction to Relativistic Quantum Field Theory. Harper & Row, New York.
- 35. Sternberg, S. (1994) Group Theory and Physics. Cambridge University Press, Cambridge.
- 36. Comay, E. (2016) Problems with Mathematically Real Quantum Wave Functions. OALib Journal, 3, 1-6.
https://www.scirp.org/journal/PaperInformation.aspx?PaperID=70117 - 37. http://news.fnal.gov/2011/11/the-standard-model-the-most-successful-theory-ever/
- 38. http://www.elliottmccrory.com/wp/2016/the-standard-model-the-most-successful-theory-ever/
- 39. https://atlasphysathome.web.cern.ch/content/standard-model
- 40. Oerter, R. (2006) The Theory of Almost Everything: The Standard Model, the Unsung Triumph of Modern Physics. Plume, New York.
- 41. https://higgs.ph.ed.ac.uk/sites/default/files/Strassler_Looking%20Beyond%20SM.pdf
- 42. Woit, P. (2006) Not Even Wrong: The Failure of String Theory and the Search for Unity in Physical Law. Basic Books, New York.
- 43. Woit, P. (2015) Towards a Grand Unified Theory of Mathematics and Physics.
https://arxiv.org/pdf/1506.07576.pdf - 44. Smolin, L. (2006) The Trouble with Physics. Houghton Mifflin, Boston.