 Open Journal of Marine Science, 2011, 3, 73-81 doi:10.4236/ojms.2011.13008 Published Online October 2011 (http://www.SciRP.org/journal/ojms) Copyright © 2011 SciRes. OJMS Parametric Linear Stochastic Modelling of Benue River Flow Process Otache Y. Martins, Isiguzo E. Ahaneku, Sadeeq A. Mohanned Department of Agricultural & Bioresources Engineering, Federal University of Technology, Minna, Nigeria E-mail: martynso_pm@yahoo.co.uk Received May 11, 2011; revised May 30, 2011; accepted July 2, 2011 Abstract The dynamics and accurate forecasting of streamflow processes of a river are important in the management of extreme events such as floods and droughts, optimal design of water storage structures and drainage net- works. In this study, attempt was made at investigating the appropriateness of stochastic modelling of the streamflow process of the Benue River using data-driven models based on univariate streamflow series. To this end, multiplicative seasonal Autoregressive Integrated Moving Average (ARIMA) model was developed for the logarithmic transformed monthly flows. The seasonal ARIMA model’s performance was compared with the traditional Thomas-Fiering model forecasts, and results obtained show that the multiplicative sea- sonal ARIMA model was able to forecast flow logarithms. However, it could not adequately account for the seasonal variability in the monthly standard deviations. The forecast flow logarithms therefore cannot read- ily be transformed into natural flows; hence, the need for cautious optimism in its adoption, though it could be used as a basis for the development of an Integrated Riverflow Forecasting System (IRFS). Since fore- casting could be a highly “noisy” application because of the complex river flow system, a distributed hydro- logical model is recommended for real-time forecasting of the river flow regime especially for purposes of sustainable water resources management. Keywords: Stochastic Process, Water Resources, Dynamics, River Flow, Modeling 1. Introduction Inherent in the principles of water resources management is the judicious utilization and conservation of the avail- able water resources. One of the ways to enhance this is the proper estimation of water demand both quantita- tively and qualitatively. Within this overall management system, the hydrologist is often required to estimate the magnitude of extreme events, whereas operation of some of the design works is often dependent on reliable esti- mates of flow for an ensuing period of time. Since river is an essential component of the hydrologic cycle, its flow forecasting provides a veritable, and basic informa- tion on a wide range of problems related to the design and operation of the entire river system. A very common constraint encountered in the context of water resources planning is inadequacy of streamflow records. The available streamflows, known as historical records, are often quite short, generally sometimes less than a quarter of a century in length. Thus, a system designed on the basis of the historical record only faces a chance of being inadequate for the unknown flow sequence that the sys- tem might experience. The historical record comprising a single short series does not cover a sequence of low flows as well as high flows. Hence, the reliability of a system has to be evaluated under these conditions which are not possible with historical records alone. Statistically, the historical record is a sample out of a population of natural streamflow process. Thus, the gen- erated flows are neither historical flows nor a prediction of future flows but rather are representative of likely flows in a stream or river. Streamflow, being a natural phenomenon, has a random component, though not fully random since it has been observed that it exhibits het- eroscedastic behavioural pattern. Forecasting river flow in general or after heavy rainfall event is important for public safety, environmental issues, and water manage- ment. For these purposes, mathematical models have been developed based either on physical considerations [1-4] or on statistical analysis [5-7]. Conventional mod- els for streamflow forecasting typically involve a number of physical variables that function as inputs. A physical  OTACHE ET AL. 74 Copyright © 2011 SciRes. OJMS variable that is not very useful for forecasting on its own can often be useful when used in conjunction with other variables. Given the number of physical variables that could be considered as potentially relevant, it is apparent that a very large number of different combinations of both variables and mathematical relationships that link them together are available when developing a stream- flow forecasting model. Determining an appropriate model structure by trial-and-error process is therefore not always practical [8]. The non-practical determinate nature of model struc- ture for streamflow/river flow forecasting can really be appreciated in a wider context considering the fact that river flow is usually treated as a random process, purely stochastic. The justification is that river flow is a func- tion of precipitation and other processes which, at pre- sent level of knowledge, seem to evolve randomly in time and space. Even if the underlying phenomena and their interactions were thoroughly understood, it would not be possible to describe mathematically the rate of discharge in a natural water course without involving unsystematic or unknown effects [9]. Considering the issues involved in river flow studies within the premise of a wider hydrological horizon, it is pertinent to appre- ciate the following seemingly, contemporaneous para- doxes: 1) In the face of the stifling dearth of long and con- tinuous data availability, can realistic generalizations be made from forecasting the dynamics of the Benue River? 2) Considering the complex nature of river flow and the significant variability it exhibits in both time and space, what is the appropriateness of using stochastic method for modelling the Benue River flow process? To this end, the objective of this study is to model the streamflow process of the Benue River with Autoregres- sive Integrated Moving Average (ARIMA) models, fo- cusing on short term forecasting for the purposes of evaluating suitability of particular model type as a pre- liminary step towards developing an enhanced “River Flow Forecasting System” for the river. 2. Materials and Methods 1) Hydrology of the Benue River The Benue River is the major tributary of the Niger River. It is approximately 1 400 km long and almost navigable during the rainy season (between July and Oc- tober). Hence, it is an important transportation route in the regions it flows through. Its headwaters rises in the Adamawa Plateau of the Northern Cameroon, flows into Nigeria south of the Mandara Mountains through the east-central part of Nigeria before entering the Niger River at Lokoja (Figure 1a). The wide flood plain is used for agriculture, with main crops being sugar cane and rice. There is only one high-water season because of its southerly location; this normally occurs from May to October, while on the other hand, the low-water period is from December to June. Figure 1b explains the hydro logical flow regime of the Benue River in line with the general climatic pattern. There are definite wet and dry seasons which give rise to changes in river flow and sa- linity regimes. The flood of the Benue River (upper, middle, and downstream) lasts from July to October, and sometimes up to early November. 2) Data Base Management In this study, historical time series for gauging stations at the base of the Benue River (i.e., Lower Benue River Basin) at Makurdi (7°44′ N, 8°32′ E) was used. A total of 26 years (1974–2000) water stage and discharge data were collected and used. The daily flow data were ag- gregated to monthly and annual data series by taking the average of each month’s flow and calendar year. Simi- larly, the annual maximum and minimum daily average discharges were obtained according to the water year, i.e., months of April to March for the streamflow process. 3) Model Formulation and Forecast Strategy The possibility of fitting a multiplicative seasonal ARIMA model to the logarithms of the monthly flows was examined. The forecasts from this model were compared to forecasting using a conventional Thomas-Fiering model. Comparison of forecast errors was also performed to bring to the fore the suitability of either of the models for forecasting the streamflow process of the river. Model formulation and development was patterned after Box and Jenkins [1], Carlson et al. [11] and McKerchar and Delleur [12]. a) Thomas-Fiering Model Thomas and Fiering [13] described a linear stochastic model for simulating synthetic flow data. On a monthly basis, this represents the means, standard deviations, serial correlations between successive flows, and the skewness. This model uses a linear regression relation- ship to relate the flow 1t Q in the (t+1)th month, (t be- ing from the start of the generated sequence) to the flow t in the t(th) month. If Q Q and 1 Q be the mean monthly discharges during months j and j+1, respectively, within a repetitive annual cycle of 12 months, b be the regression coefficient for estimating the flow in the (j+1)th month from the jth month, and tt be a normal de- viate with zero mean and unit variance, the Tho- mas-Fiering equation will be 12 2 11 1 1 tjjtjtj j QQ bQQtr (1) If an average first-order serial correlation coefficient r1 is used to replace the 12 monthly rj values, it can easily be shown using the relationship  OTACHE ET AL. 75 (a) (b) Figure 1. (a) Map of Nigeria showing Benue River and its traverse; (b) general hydrological year flow regime Copyright © 2011 SciRes. OJMS 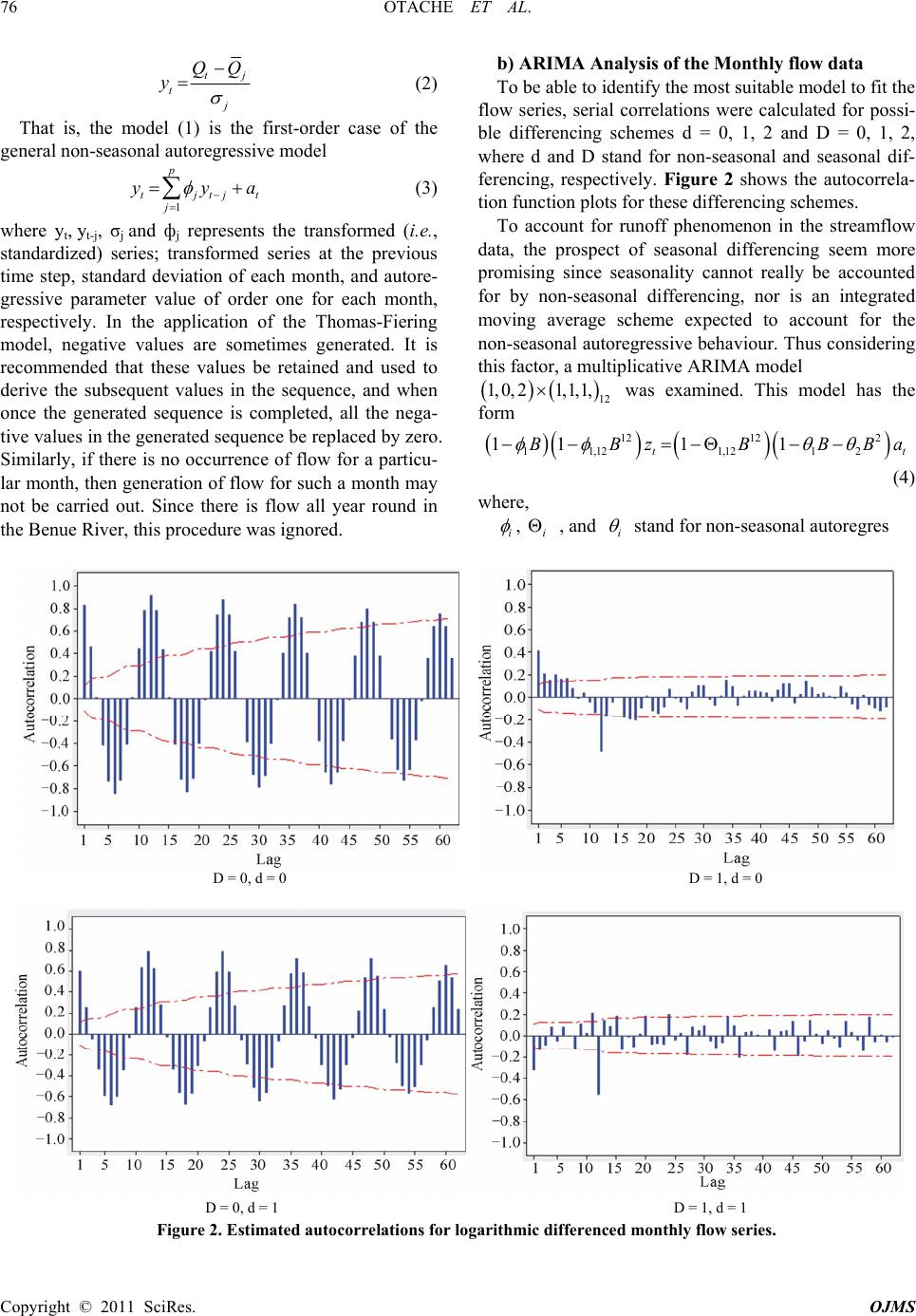 OTACHE ET AL. 76 t tj QQ y Copyright © 2011 SciRes. OJMS j t a (2) That is, the model (1) is the first-order case of the general non-seasonal autoregressive model 1 p tjtj j yy (3) where yt, yt-j, σj and фj represents the transformed (i.e., standardized) series; transformed series at the previous time step, standard deviation of each month, and autore- gressive parameter value of order one for each month, respectively. In the application of the Thomas-Fiering model, negative values are sometimes generated. It is recommended that these values be retained and used to derive the subsequent values in the sequence, and when once the generated sequence is completed, all the nega- tive values in the generated sequence be replaced by zero. Similarly, if there is no occurrence of flow for a particu- lar month, then generation of flow for such a month may not be carried out. Since there is flow all year round in the Benue River, this procedure was ignored. b) AR IMA Analysis of the Monthly flow data To be able to identify the most suitable model to fit the flow series, serial correlations were calculated for possi- ble differencing schemes d = 0, 1, 2 and D = 0, 1, 2, where d and D stand for non-seasonal and seasonal dif- ferencing, respectively. Figure 2 shows the autocorrela- tion function plots for these differencing schemes. To account for runoff phenomenon in the streamflow data, the prospect of seasonal differencing seem more promising since seasonality cannot really be accounted for by non-seasonal differencing, nor is an integrated moving average scheme expected to account for the non-seasonal autoregressive behaviour. Thus considering this factor, a multiplicative ARIMA model 12 1, 0,21,1,1, was examined. This model has the form 1212 2 11,121,121 2 111 1 tt BBz BBB a (4) where, i , i , and i stand for non-seasonal autoregres D = 0, d = 0 D = 1, d = 0 D = 0, d = 1 D = 1, d = 1 Figure 2. Estimated autocorrelations for logarithmic differenced monthly flow series. 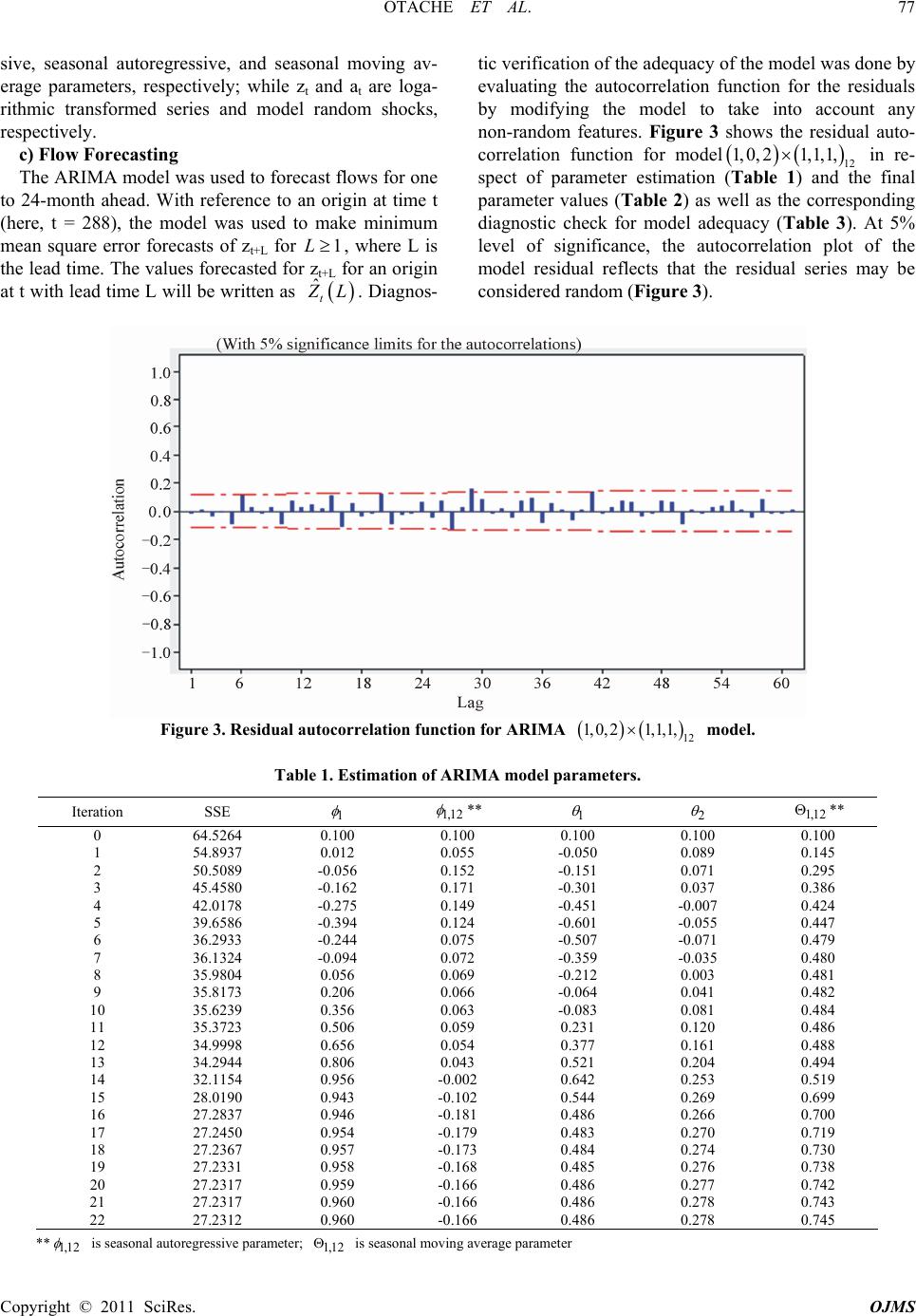 OTACHE ET AL. 77 sive, seasonal autoregressive, and seasonal moving av- erage parameters, respectively; while z t and a t are loga- rithmic transformed series and model random shocks, respectively. c) Flow Forecasting The ARIMA model was used to forecast flows for one to 24-month ahead. With reference to an origin at time t (here, t = 288), the model was used to make minimum mean square error forecasts of z t+L for, where L is the lead time. The values forecasted for z t+L for an origin at t with lead time L will be written as 1L ˆ t L. Diagnos- tic verification of the adequacy of the model was done by evaluating the autocorrelation function for the residuals by modifying the model to take into account any non-random features. Figure 3 shows the residual auto- correlation function for model 12 in re- spect of parameter estimation (Table 1) and the final parameter values (Table 2) as well as the corresponding diagnostic check for model adequacy (Table 3). At 5% level of significance, the autocorrelation plot of the model residual reflects that the residual series may be considered random (Figure 3). 1, 0,21,1,1, Figure 3. Residual autocorrelation function for ARIMA 12 1, 0,21,1,1, model. Table 1. Estimation of ARIMA model parameters. Iteration SSE 1 1,12 ** 1 2 1,12 ** 0 64.5264 0.100 0.100 0.100 0.100 0.100 1 54.8937 0.012 0.055 -0.050 0.089 0.145 2 50.5089 -0.056 0.152 -0.151 0.071 0.295 3 45.4580 -0.162 0.171 -0.301 0.037 0.386 4 42.0178 -0.275 0.149 -0.451 -0.007 0.424 5 39.6586 -0.394 0.124 -0.601 -0.055 0.447 6 36.2933 -0.244 0.075 -0.507 -0.071 0.479 7 36.1324 -0.094 0.072 -0.359 -0.035 0.480 8 35.9804 0.056 0.069 -0.212 0.003 0.481 9 35.8173 0.206 0.066 -0.064 0.041 0.482 10 35.6239 0.356 0.063 -0.083 0.081 0.484 11 35.3723 0.506 0.059 0.231 0.120 0.486 12 34.9998 0.656 0.054 0.377 0.161 0.488 13 34.2944 0.806 0.043 0.521 0.204 0.494 14 32.1154 0.956 -0.002 0.642 0.253 0.519 15 28.0190 0.943 -0.102 0.544 0.269 0.699 16 27.2837 0.946 -0.181 0.486 0.266 0.700 17 27.2450 0.954 -0.179 0.483 0.270 0.719 18 27.2367 0.957 -0.173 0.484 0.274 0.730 19 27.2331 0.958 -0.168 0.485 0.276 0.738 20 27.2317 0.959 -0.166 0.486 0.277 0.742 21 27.2317 0.960 -0.166 0.486 0.278 0.743 22 27.2312 0.960 -0.166 0.486 0.278 0.745 ** is seasonal autoregressive parameter; is seasonal moving average parameter 1,12 1,12 Copyright © 2011 SciRes. OJMS  OTACHE ET AL. 78 Copyright © 2011 SciRes. OJMS Table 2. Final model parameter estimates. Parameters Statistics Type Coef SE Coef T P AR 1 0.9600 0.0284 33.83 0.000 SAR 12** -0.1657 0.0748 -2.22 0.028 MA1 0.4859 0.0667 7.29 0.000 MA 2 0.2782 0.0646 4.31 0.000 SMA 12* 0.7447 0.0544 13.69 0.000 Constant 0.000318 0.001155 0.28 0.783 ** Seasonal autoregressive parameter, * seasonal moving average parameter Table 3. Modified Box-Pierce (L jung-Box) Chi-Square statistic. Lag 12 24 36 48 Chi-Square 10.2 29.0 46.3 60.4 Critical value 12.6 28.9 43.8 58.1 DF 6 18 30 42 In terms of the forecasting function, the general ARIMA model can be written in three alternative forms: as a difference equation, an infinite sum of the current and weighted previous values of shocks at, and an infi- nite sum of weighted previous observations plus the cur- rent value of at. Conditional expectation of any of these forms supplies a forecasting function. In this regard, the difference equation was used. By recalling that tt ZL Z L , using square brackets to signify condi- tional expectation, noting that 1 11 0,1, 2, ˆ1, 2, ˆ10,1,2, 0 tjtj tt tjttj tj tj zz j zzjj aazzj a 1 ,2,j t a (5) and taking expectation of the model, which has the general form 1212 2 11,121,121 2 111 1 t BBz BBB , the forecasting function can be obtained according as: 111,12 1211,1213 11 221,1212 1 1,121321,1214 tL tLtLtL tL tLtLtL tL tL zz zz aa aa aa the model fit was done with 26 years of flow data). The 3. Results and Discussion Figure 4 shows the behaviour of the ARIMA model (6) Equation (6) can be expanded for the respective lead time (L) to make the forecasts with zt+L, the dependent forecast variable as a function of L. Both the Thomas Fiering and ARIMA models were used to make forecasts of the monthly flow series. Subsequently, the forecasts from the models were compared with the actual flows. Because the last 2 years flow data was used for the com- parison, the parameters were re-estimated for both mod- els for the entire flow series shortened by 2 years (i.e., flow forecasts were considered from the aspect of choosing a particular time origin and taking cognizance of the behaviour of the forecast function as the lead time L increases; that is, the long-term behaviour of the fore- cast function should be a useful theoretical check on the fit of a model. Taking the origin t = 288, forecasts for the logarithms of the flow were made using both models. forecast function; the forecasts are quite close to the monthly means. Baring data quality problems, stationar- ity issues, and model over-fitting, for an ideal forecast function, this behaviour is to be expected. Forecasts in the distant future for a trend-free series should be the unconditional estimates of the means. Figure 5 indicates that the forecasts are all within the bounds with respect to actual flows. Based on this, and taking into considera- tion the data size for model fitting, the ARIMA model has reproduced the monthly means well. Figure 6 illus- trates the standard errors of the forecasts. This figure compares the monthly standard deviations of the loga- rithms of the monthly flow with the standard errors for forecasts of the two models under discourse, respectively, for 124L . As L becomes large (say, greater than 4), the error of a forecast for Thomas-Fiering model, tends closely to that of the historic flow, whereas the ARIMA model deviates away significantly. The be- haviour of the Thomas-Fiering model in this regard is further explained by Figure 7, where it was used to simulate the flow regime for 26 years. It was able to re- produce the flow dynamics clearly well. This attribute reinforces its suitability to be used for long-term flow forecasting of the Benue River. The failure of the ARIMA model to account for the seasonal pattern in the standard deviations is a major limitation of the model. In standard 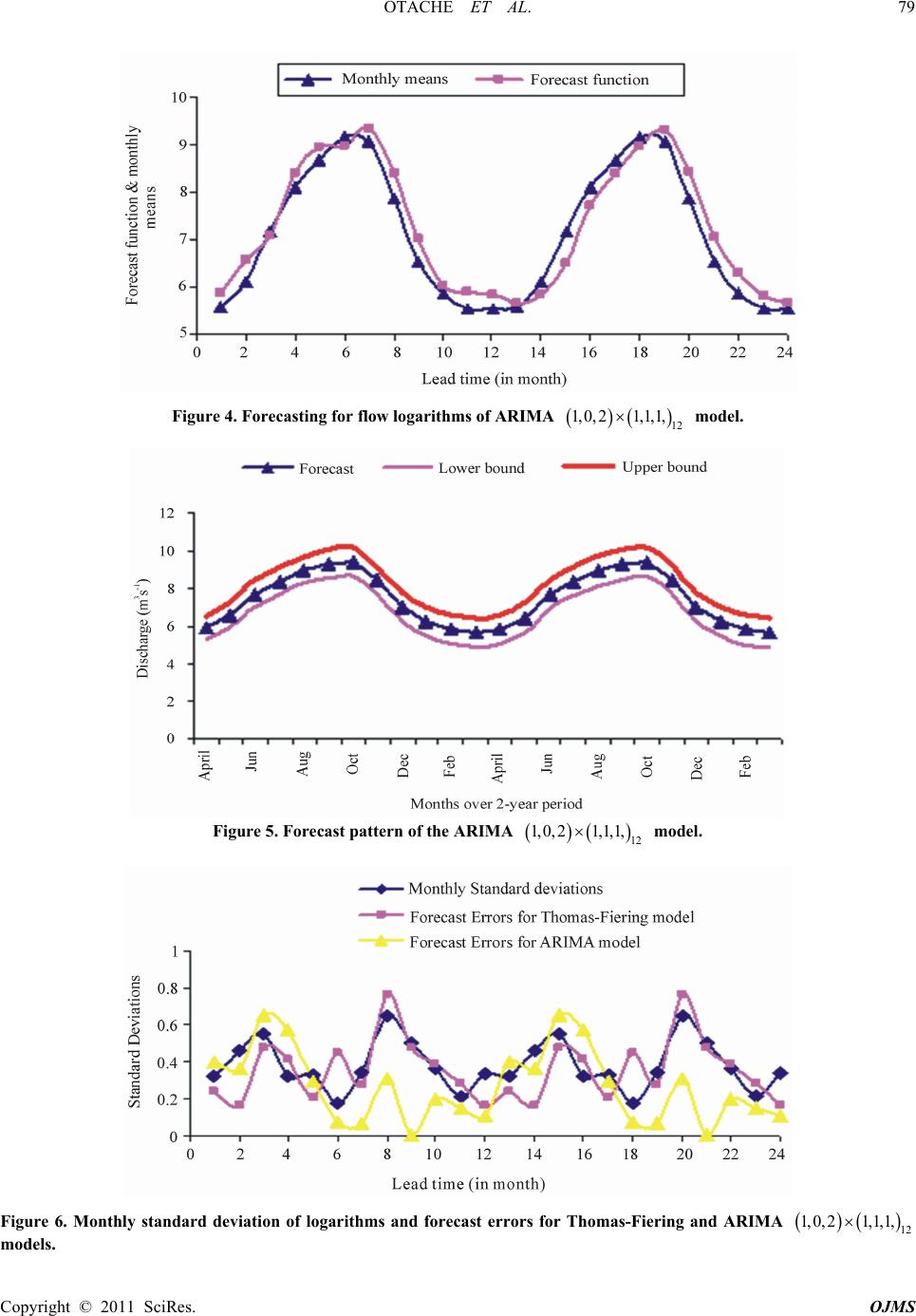 OTACHE ET AL. 79 12 1, 0, 21,1,1, modelFigure 4. Forecasting for flow logarithms of ARIMA . 12 1, 0, 21,1,1, moFigure 5. Forecast pattern of the ARIMA del. Figure 6. Monthly standard deviation of logarithms and forecast errors for Thomas-Fiering and ARIMA 12 1, 0, 21,1,1, models. Copyright © 2011 SciRes. OJMS 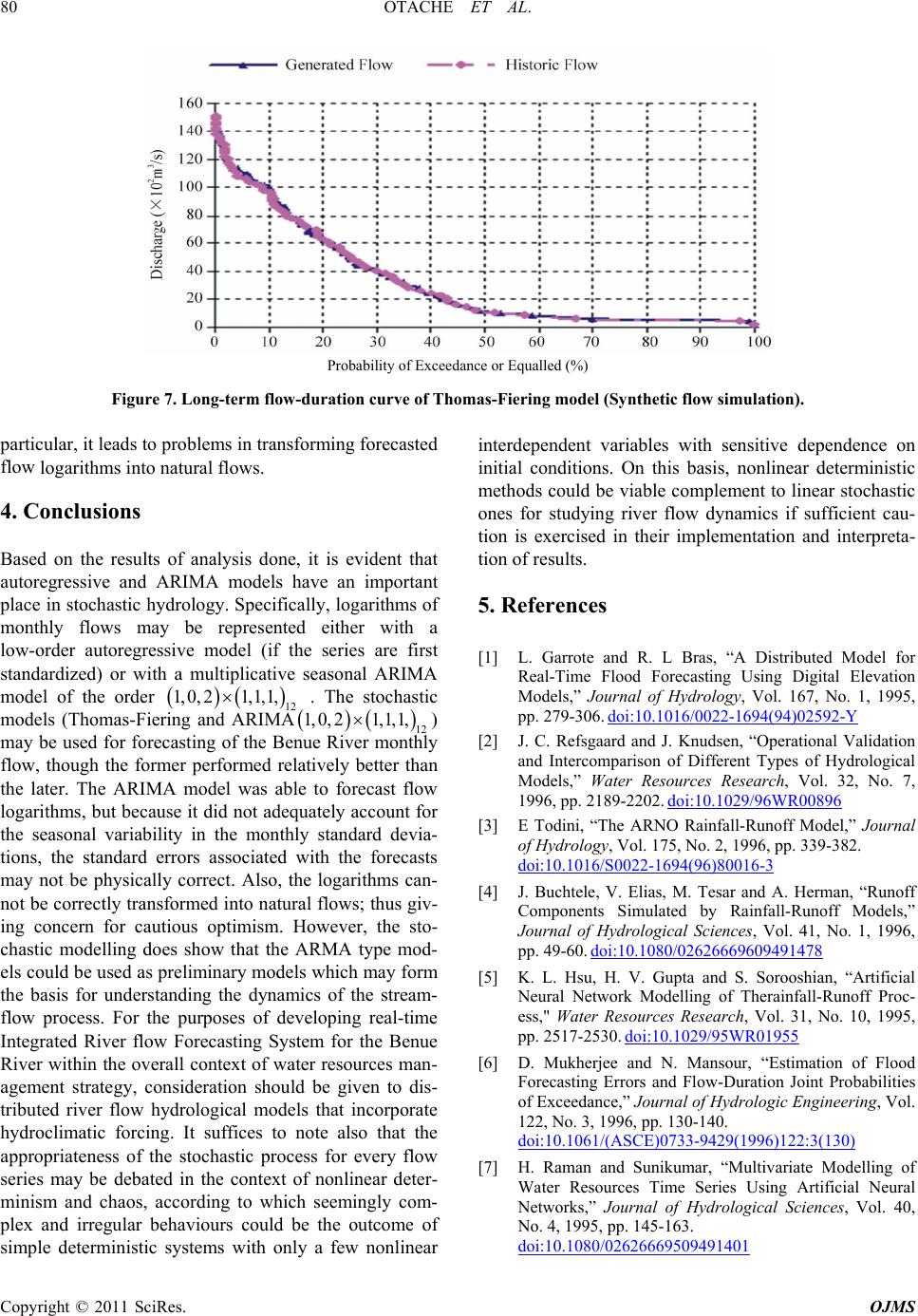 OTACHE ET AL. Copyright © 2011 SciRes. OJMS 80 Probability of Exceedance or Equalled (%) Figure 7. Long-term flow-duration curve of Tynthetic flow simulation). articular, it leads to problems in transforming forecasted . Conclusions ased on the results of analysis done, it is evident that homas-Fiering model (S p flow logarithms into natural flows. 4 B autoregressive and ARIMA models have an important place in stochastic hydrology. Specifically, logarithms of monthly flows may be represented either with a low-order autoregressive model (if the series are first standardized) or with a multiplicative seasonal ARIMA model of the order 12 1, 0,21,1,1, . The stochastic models (Thomas-Fier ing and ARIMA 12 1, 0,21,1,1, ) may be used for forecasting of the Benuey flow, though the former performed relatively better than the later. The ARIMA model was able to forecast flow logarithms, but because it did not adequately account for the seasonal variability in the monthly standard devia- tions, the standard errors associated with the forecasts may not be physically correct. Also, the logarithms can- not be correctly transformed into natural flows; thus giv- ing concern for cautious optimism. However, the sto- chastic modelling does show that the ARMA type mod- els could be used as preliminary models which may form the basis for understanding the dynamics of the stream- flow process. For the purposes of developing real-time Integrated River flow Forecasting System for the Benue River within the overall context of water resources man- agement strategy, consideration should be given to dis- tributed river flow hydrological models that incorporate hydroclimatic forcing. It suffices to note also that the appropriateness of the stochastic process for every flow series may be debated in the context of nonlinear deter- minism and chaos, according to which seemingly com- plex and irregular behaviours could be the outcome of simple deterministic systems with only a few nonlinear initial conditions. On this basis, nonlinear deterministic methods could be viable complement to linear stochastic ones for studying river flow dynamics if sufficient cau- tion is exercised in their implementation and interpreta- tion of results. 5. Reference River monthl interdependent variables with sensitive dependence on s d R. L Bras, “A Distributed Model for Real-Time Flood Forecasting Using Digital Elevation [1] L. Garrote an Models,” Journal of Hydrology, Vol. 167, No. 1, 1995, pp. 279-306. doi:10.1016/0022-1694(94)02592-Y [2] J. C. Refsgaard and J. Knudsen, “Operational Validation and Intercomparison of Different Types of Hydrological Models,” Water Resources Research, Vol. 32, No. 7, 1996, pp. 2189-2202. doi:10.1029/96WR00896 [3] E Todini, “The ARNO Rainfall-Runoff Model,” Journal of Hydrology, Vol. 175, No. 2, 1996, pp. 339-382. doi:10.1016/S0022-1694(96)80016-3 [4] J. Buchtele, V. Elias, M. Tesar and A. Herman, “R Components Simulated by Rainfall unoff -Runoff Models,” Journal of Hydrological Sciences, Vol. 41, No. 1, 1996, pp. 49-60. doi:10.1080/02626669609491478 [5] K. L. Hsu, H. V. Gupta and S. Sorooshian, “Artificial Neural Network Modelling of Therainfall-Runoff Proc- ess," Water Resources Research, Vol. 31, No. 10, 1995, pp. 2517-2530. doi:10.1029/95WR01955 [6] D. Mukherjee and N. Mansour, “Estimation of Flood Forecasting Errors and Flow-Duration Joint Probabilities of Exceedance,” Journal of Hydrologic Engineering, Vol. 122, No. 3, 1996, pp. 130-140. doi:10.1061/(ASCE)0733-9429(1996)122:3(130) [7] H. Raman and Sunikumar, “M Water Resources Time Series Using Artificial Neural ultivariate Modelling of Networks,” Journal of Hydrological Sciences, Vol. 40, No. 4, 1995, pp. 145-163. doi:10.1080/02626669509491401  OTACHE ET AL.81 Copyright © 2011 SciRes. OJMS n and S. P. Simonovic, “Short al Neural Networks. [8] C. M. Zealand, D. H. Bur Term Forecasting Using Artifici Journal of Hydrology, Vol. 214, No. 1-4, 1999, pp. 32-48. doi:10.1016/S0022-1694(98)00242-X [9] N. T. Kottegoda, “Stochastic Water Resources Technol- ogy,” The Macmillan Press Ltd, London, 1980, pp. 2-3, nd Control,” Holden-Day Press, San F m Models to Four Annual Flow 21, 112-113. [10] G. E. P. Box and G. M Jenkins, “Time Series Analysis Forecasting aran- cisco, 1976, pp. 32-100. [11] R. F. Carlson, A. J. A. McCormick and D. G. Watts, “Ap- plication of Linear Rando Series,” Water Resources Research, Vol. 6, No. 4, 1970, pp. 1070-1078. doi:10.1029/WR006i004p01070 [12] A. I. McKerchar and J. W. Delleur, “Application of Sea- sonal Parametric Linear Stochastic Models to Monthly Flow Data,” Water Resources Research, Vol. 10, No. 2, 1974, pp. 246-254. doi:10.1029/WR010i002p00246 [13] H. A. Thomas and M. B. Fiering, “Mathematical Synthe- sis of Streamflow Sequences for the Analysis of River Basins by Simulations,” In Design of Water Resource Systems, Edited by Mass et al., Harvard University Press, Cambridge, 1962, pp. 459-493.
|