Atmospheric and Climate Sciences, 2011, 1, 197-205
doi:10.4236/acs.2011.14022 Published Online October 2011 (http://www.SciRP.org/journal/acs)
A Probe for Consistency in CAPE and CINE during
the Prevalence of Severe Thunderstorms:
Statistical-Fuzzy Coupled Approach
Sutapa Chaudhuri
Department of Atmos p heri c S ci ences , University of Calcutta, Kolka ta, India
Received May 16, 2011; revised July 1, 2011; accepted July 20, 2011
Abstract
Thunderstorms of pre-monsoon season (April-May) over Kolkata (22˚32' N, 88˚20' E), India are invariably
accompanied with lightning flashes, high wind gusts, torrential rainfall, occasional hail and tornadoes which
significantly affect the life and property on the ground and aviation aloft. The societal and economic impact
due to such storms made accurate prediction of the weather phenomenon a serious concern for the meteor-
ologists of India. The initiation of such storms requires sufficient moisture in lower troposphere, high surface
temperature, conditional instability and a source of lift to initiate the convection. Convective available poten-
tial energy (CAPE) is a measure of the energy realized when conditional instability is released. It plays an
important role in meso-scale convective systems. Convective inhibition energy (CINE) on the other hand
acts as a possible barrier to the release of convection even in the presence of high value of CAPE. The main
idea of the present study is to see whether a consistent quantitative range of CAPE and CINE can be identi-
fied for the prevalence of such thunderstorms that may aid in operational forecast. A statistical-fuzzy coupled
method is implemented for the purpose. The result reveals that a definite range of CINE within 0 - 150 J·kg–1
is reasonably pertinent whereas no such range of CAPE depicts any consistency for the occurrence of severe
thunderstorms over Kolkata. The measure of CINE mainly depends upon the altitude of the level of free
convection (LFC), surface temperature (T) and surface mixing ratio (q). The box-and-whisker plot of LFC, T
and q are drawn to select the most dependable parameter for the consistency of CINE in the prevalence of
such thunderstorms. The skills of the parameters are evaluated through skill score analyses. The percentage
error during validation with the observation of 2010 is estimated to be 0% for the range of CINE and 3.9%
for CAPE.
Keywords: Severe Thunderstorms, Forecast, CAPE, CINE, Statistics, Fuzzy Logic
1. Introduction
Thunderstorms of pre-monsoon season (April-May) over
Kolkata (22˚32' N, 88˚20' E, India are local severe stor-
ms, termed as Nor’westers because the approach of these
storms towards the station is predominantly from the
north-westerly direction and are locally known as “Kal-
baishakhi” meaning “danger in the month of Baishakh”. In
general, thunderstorms are recurrent features and prevail
over different parts of India. However, Nor’westers leads
to remarkable devastation causing significant socio-eco-
nomic impact over the region due to loss of life and prop-
erty and aviation hazard. Precise forecast of Nor’westers
continues to be a challenge for the atmospheric scientists
of India. This has, doubtless, occupied the attention of
the meteorologists over the last nine decades or so. Ini-
tially all the investigations were based on the observa-
tions of surface parameters before and immediately after
the occurrence of thunderstorms. Priority was given to
thermodynamic parameters especially the wet bulb and
wet bulb potential temperature [1]. Indian meteorologists
[2] could identify well before the publication of thunder-
storm project report in United States [3] that not only the
discontinuity in temperature and moisture in the vertical
plane was a favorable environment for the genesis of
such thunderstorms but the large-scale flow pattern to

S. CHAUDHURI
198
advect temperature and moisture were also important. A
major contribution was made by introducing the micro-
physics of cloud in explaining updraft and down draft [4].
Initially, the primary importance was given to the low
level features [5] and later the upper atmosphere was
observed to be a prime promoter of deep convection [6].
Coupling of low level and upper level features was then
suggested to be important [7]. Theory of excessive over-
shooting proved the validity of parcel convection in some
form [8]. The significant parameters for the prediction
of pre-monsoon thunderstorms at Kolkata were identified
using statistical methods [9]. The level of downdraft for-
mation was identified during Nor’westers using frequency
domain analysis [10]. The multivariate technique was
applied to reduce the number of variables in forecasting
pre-monsoon thunderstorms [11]. The consequences,
before and after the occurrence of Nor’westers were
brought into the knowledge using statistical method [12].
Some cases of Nor’westers were simulated by different
numerical models [13-15].
Probably due to the complex nature of the pheno-
menon and non-availability of the proper network of
observations, no single technique, so far, has proven to
be sufficient enough for the accurate prediction of
Nor’westers. The complex nature and non-linearity in-
herent in the atmospheric processes necessitated a way
out from the existing conventional methods.
The application of artificial intelligence (AI) in the
form of soft computing technique [16] in atmospheric
sciences has become very popular since 1990s. Many
scientists have used AI methods in meteorology [17-27].
The method of genetic algorithm (GA) is observed to
be useful to identify the appropriate energy required for
the genesis of severe thunderstorms over Kolkata [28].
The method of ampliative reasoning is used to identify
the critical values of CAPE and CINE for definite occur-
rence of severe thunderstorms [29]. Artificial Neural
Network (ANN) model is developed to forecast the
maximum wind speed associated with severe thunder-
storms over Kolkata [30]. The depth of the potential
convective instability during Nor’westers was quantified
using a hybrid soft computing model [31]. The convec-
tive available potential energy (CAPE) is observed to
play a significant role in linking the thermodynamics and
microphysical processes during severe thunderstorms
[32]. The significance of the shape of CAPE in estimate-
ing the severity of pre-monsoon thunderstorm over Kol-
kata was established using chaotic graph theory [33]. The
consequence of surface parameters due to the occurrence
of severe thunderstorms is observed with rough set theory
[34]. Preferred sequence of low level clouds for the de-
velopment of severe thunderstorms was identified using
soft computing technique [35]. The importance of 06
UTC observations in the study of Nor’westers is empha-
sized in the paper. Bipartite graph model is developed for
forecasting thunderstorm over Kolkata [36]. The model
provides 12 hour forecast (nowcasting) of thunder-
storms with 96% accuracy. The significance of convec-
tive energies in forecasting severe thunderstorms is pre-
sented with one hidden layer neural net and variable
learning rate back propagation algorithm [37]. The con-
cept of fractal dimension is introduced in the study of
pre-monsoon thunderstorms [38]. Graph spectral distan-
ce and entropy estimation are implemented for nowcast-
ing thunderstorms [39].
The main objective of the study is to reveal a depen-
dable quantitative range of CAPE and CINE for the
prevalence of severe thunderstorms over Kolkata during
the premonsoon season, which may abet in the opera-
tional forecast of the weather system.
2. Materials and Methods
2.1. Meteorological Data
The upper air Radiosonde (RS)/Rawinsonde (RW) data
at 00 and 12 UTC used in the present study are collected
from the website of the Department of Atmospheric Sci-
ence, University of Wyoming for the pre-monsoon sea-
son (April-May) during the period from 1997 to 2009.
The location of the study is Kolkata (22˚32' N, 88˚20' E)
(station no. 42809). The record of the occurrences of
thunderstorms is collected from Regional Meteorologi-
cal Centre, (RMC), Kolkata, India. The records include
the time of occurrence, duration, maximum wind speed,
direction of squall advancement and available satellite
and radar observations.
The input variables used in the present study are the
RS/RW sounding data at the UTC before the occur-
rence of thunderstorms. The convective available poten-
tial energy (CAPE), convective inhibition energy (CINE),
altitude of the level of free convection (LFC) from the
surface level are computed using the RAOB (Rawin-
sonde Observation) software and taken as the input pa-
rameters along with the surface temperature and surface
mixing ratio for implementing the coupled approach of
statistics and fuzzy theory. The variability in the altitude
of LFC, surface temperature and surface mixing ratio are
estimated using box-whisker plots.The Thunderstorm
days of 2010 are selected for the validation of the result
with the observation.
2.2. Methodology
The methodology in this study includes the Z-statistics of
the statistical hypothesis testing to identify the quanti-

S. CHAUDHURI 199
,
tative ranges of CAPE and CINE for the occurrence of
severe thunderstorms. The fuzzy membership is imple-
mented to discern the significance of the linguistic vari-
ables “more” in relation to the consistency of the ranges
of CAPE and CINE. The box-and-whisker plot are drawn
to view the variability in the altitude of LFC, surface
temperature (T) and surface mixing ratio (q) during se-
vere thunderstorms. According to Wilks [40], accuracy is
simply the correspondence between the observations and
forecasts while forecast skill refers to the accuracy of a
forecast set relative to a set of control forecasts, an im-
provement over a control forecast set. The Heidke Skill
Score (HSS) uses random forecasts as the control set.
However, Jolliffe and Stephenson [41] demonstrated that
Odds Ratio Skill Score (Yule’s Q) is more preferable
than HSS in evaluating the performance of binary fore-
casts since Yule’s Q satisfies the criteria of equitability,
regularity, and consistency where as HSS satisfies only
the equitability. Nevertheless, either HSS or Yule’s Q
should provide a better assessment of performance. A
contingency table is prepared and the Yule’s Q, True
Skill Statistics (TSS) and Hiedke Skill Score (HSS) are
computed to identify the skill of the parameters.
2.2.1. Statistical Hypoth esi s T e stin g
Meteorological data analysis and making prediction
based on these data requires a huge archive of data. The
weather prediction cannot be made accurate unless it is
made on the basis of a sample data having adequate ver-
satility because the nonlinearity and complexity are in-
herent in the atmospheric processes. The implementa-
tion of the logic of hypothesis testing thus becomes nec-
essary [42]. Several statistics are used in testing different
hypotheses. Use of a particular statistic depends upon the
type of the problem. In the present study, Z-statistic is
used.
A sample of 124 severe thunderstorms with wind
speed more than 65 km·h1 during the period from 1997
to 2009 in the pre-monsoon season (April-May) is col-
lected for this study.
The frequencies of the occurrence of thunderstorms
for different ranges of CAPE and CINE are computed
during the pre monsoon season over Kolkata within the
period from 1997 to 2009 (Table 1).
This gives a mean CINE
x
= 131 and a standard
deviation of CINE = 102.78.
The mean CINE is assumed to be 150 J·kg1 in this
study because the maximum number of thunderstorms
occurred for CINE within the range of 0 to 150 J·kg1.
The null hypothesis in case of CINE is thus, defined
as:H0:  = 150.
Without contradicting the observational records, an
alternative hypothesis becomes:
Table 1. Frequency (percentage) of pre-monsoon thunder-
storms over Kolkata within different ranges of CAPE and
CINE.
CAPE (J·kg1)CINE (J·kg1)
0 - 150151 - 300 301 - 450 451 - 600Total
0000 - 100016
(12.9%)
16
(12.9%)
07
(5.7%)
00
(0%)
39
(31.5%)
1000 - 200025
(20.2%)
07
(5.6%)
02
(1.6%)
00
(0%)
34
(27.4%)
2000 - 300022
(17.7%)
04
(3.2%)
00
(0%)
01
(1%)
27
(21.9%)
> 3000 24
(19.4%)
00
(0%)
00
(0%)
00
(0%)
24
19.4%)
Total 87 27 09 01 124
(70.2%)(21.7%) (7.3%) (1%) (100%)
H1:  < 150
A one-tailed test is performed in this case. As the
variance of CINE associated with the occurrence of
thunderstorms is not known, the standard deviation ˆ

is estimated:
ˆ

= SD = 103.19 (1)
where n = 124.
The test-statistic, Z = (–) 2.053
and Z
0.05 = 1.645 [from standard table]
The result shows that the absolute value of the test-
statistic, Z computed for the samples exceeds the tabular
value at 5% level of significance (Figure 1). Thus, null
hypothesis is rejected and the alternative hypothesis is
accepted. This indicates that, in 95% cases the mean
value of CINE for the occurrence of pre-monsoon thun-
derstorms will be less than 150 J·kg–1.
To fix the range of CINE, a two-tailed test is to be
performed.
The test-statistic in this case is
Z0.025 = 1.96 [from standard table]
because Z = Z if Z > 0
and Z = () Z if Z < 0 [by definition]
Using the Equation (2) (Wilks, 1995):

0
n
PZAP xA





 





(2)
We obtain:
P [113    148] = 95% (3)
where, P  Probability.
It is thus, observed that if 124 samples of severe thun-
derstorms of pre-monsoon season are repeatedly col-
lected then 95% of the average CINE associated with the
maximum frequency of severe thunderstorms will be
within the range of 113 to 148 J·kg1. This finding does
not involve serious Type-1 error and is, therefore rea-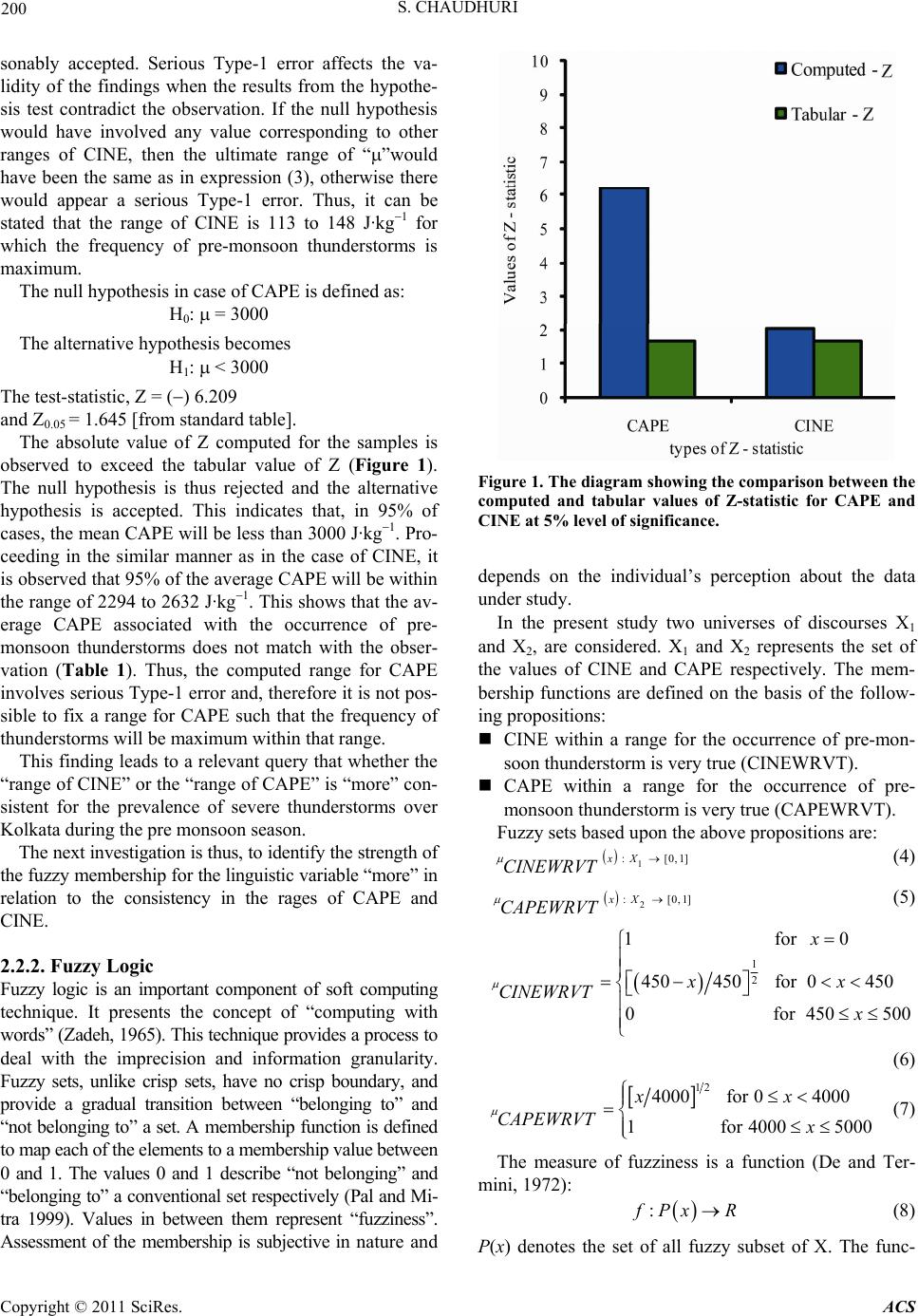

S. CHAUDHURI
200
sonably accepted. Serious Type-1 error affects the va-
lidity of the findings when the results from the hypothe-
sis test contradict the observation. If the null hypothesis
would have involved any value corresponding to other
ranges of CINE, then the ultimate range of “”would
have been the same as in expression (3), otherwise there
would appear a serious Type-1 error. Thus, it can be
stated that the range of CINE is 113 to 148 J·kg1 for
which the frequency of pre-monsoon thunderstorms is
maximum.
The null hypothesis in case of CAPE is defined as:
H0:  = 3000
The alternative hypothesis becomes
H1:  < 3000
The test-statistic, Z = () 6.209
and Z0.05 = 1.645 [from standard table].
The absolute value of Z computed for the samples is
observed to exceed the tabular value of Z (Figure 1).
The null hypothesis is thus rejected and the alternative
hypothesis is accepted. This indicates that, in 95% of
cases, the mean CAPE will be less than 3000 J·kg1. Pro-
ceeding in the similar manner as in the case of CINE, it
is observed that 95% of the average CAPE will be within
the range of 2294 to 2632 J·kg1. This shows that the av-
erage CAPE associated with the occurrence of pre-
monsoon thunderstorms does not match with the obser-
vation (Table 1). Thus, the computed range for CAPE
involves serious Type-1 error and, therefore it is not pos-
sible to fix a range for CAPE such that the frequency of
thunderstorms will be maximum within that range.
This finding leads to a relevant query that whether the
“range of CINE” or the “range of CAPE” is “more” con-
sistent for the prevalence of severe thunderstorms over
Kolkata during the pre monsoon season.
The next investigation is thus, to identify the strength of
the fuzzy membership for the linguistic variable “more” in
relation to the consistency in the rages of CAPE and
CINE.
2.2.2. Fuzzy Logic
Fuzzy logic is an important component of soft computing
technique. It presents the concept of “computing with
words” (Zadeh, 1965). This technique provides a process to
deal with the imprecision and information granularity.
Fuzzy sets, unlike crisp sets, have no crisp boundary, and
provide a gradual transition between “belonging to” and
“not belonging to” a set. A membership function is defined
to map each of the elements to a membership value between
0 and 1. The values 0 and 1 describe “not belonging” and
“belonging to” a conventional set respectively (Pal and Mi-
tra 1999). Values in between them represent “fuzziness”.
Assessment of the membership is subjective in nature and
Figure 1. The diagram showing the comparison between the
computed and tabular values of Z-statistic for CAPE and
CINE at 5% level of significance.
depends on the individual’s perception about the data
under study.
In the present study two universes of discourses X1
and X2, are considered. X1 and X2 represents the set of
the values of CINE and CAPE respectively. The mem-
bership functions are defined on the basis of the follow-
ing propositions:
 CINE within a range for the occurrence of pre-mon-
soon thunderstorm is very true (CINEWRVT).
 CAPE within a range for the occurrence of pre-
monsoon thunderstorm is very true (CAPEWRVT).
Fuzzy sets based upon the above propositions are:

1
:[0,xX
CINEWRVT
 1
,1]
] (4)

2
:[0xX
CAPEWRVT
  (5)

1
2
1 for 0
450450for 0450
0 for 450500
x
xx
CINEWRVT x





 




(6)

12
4000for 04000
1 for 40005000
xx
CAPEWRVT x






(7)
The measure of fuzziness is a function (De and Ter-
mini, 1972):


:
f
Px R (8)
P(x) denotes the set of all fuzzy subset of X. The func-

S. CHAUDHURI 201


 

tion “f” assigns to each fuzzy subset A of Xa value f(A)
that characterizes the degree of fuzziness of A.
The function “f” satisfies the following conditions:
 f(A) = 0 iff A is a crisp set.
 If AB, then f(A)f(B)
 f(A) is maximum when A is maximally fuzzy.
In general, measure of fuzziness can be expressed as:

() xA
xX
fA hgx 



 

 (9)

x
g
Xx is defined as:


:0,1
x
g
R  (10)
The functions
x
g
may be different for different x. It
is monotonically increasing in [0, 1/2] and monotonically
decreasing in [1/2, 1].
 
01
xx
gg0 (11)
x
g
(1/2) is the unique maximum of
x
g
.
Entropy is defined as a measure of fuzziness (Kosko,
1986):
 

()ln 1 ln1
xX
f
xxxx
AA AA
 

x

 
 

 

(12)
Equation (12) is a particular term of (11) with










ln1ln1
xAA AAA
g
xxx x      
x


3)
Fuzzy correlation gives a degree of association be
tween a fuzzy set and its nearest crisp set (Ghosh
G

(1
-
and
hosh, 2003);
 
12
4
,1 ()
n
Cii    
1 2
12
i
XX





(15)
 (14)

2
11
1
2()1
n
i
Xi 




2
22
1
2()1
n
i
Xi 


 (16)
1()i

represents the membership function of the fuzzy set
and 2()i

represents the characteristic function of the
ordin
hisker Diagram
The box-and-whisker plot is a histogram-like method of
onvenient, non-
Thstical skill score analysis for each parameter is done
ere the logic is “if
ary or crisp set.
2.2.3. The Box-and-W
displaying data (Tukey, 1977). It is a c
parametric way of graphically depicting groups of nu-
merical data using mean/median, upper and lower quar-
tiles, maximum and minimum value. The spacing be-
tween the different parts of the box helps to indicate the
degree of distribution and skewness inherent in the data.
The advantage of the box and whisker plot is its ability to
compare multiple datasets side-by-side. This non-parametric
statistics has been applied to meteorological, hydrologi-
cal data sets (Grumm and Hart, 2001; Thompson et al.
2007) for better visualization of skewness and dispersion.
The box-whisker diagram is drawn with the values of
LFC, T and q to identify the most consistent parameters.
2.2.4. Statistical Skill Sco re Analysis
e stati
using the contingency table (Table 2) wh
severe thunderstorms occur then 1 otherwise 0”. The statis-
tical skill score parameters considered in this study are
Yule’s Q, true skill statistic (TSS) and Heidke skill score
(HSS) (Jolliffe and Stephenson, 2003).
Yule’s Q satisfies the criteria of equitability, regularity,
and consistency and it is computed as
Yule’s Q = ()
()
ad bc
ad bc

 (17)
The worstle’s Q is 0
is 1.
Negative values would be associated with “bad”
fo
possible Yu and the best possible
TSS has a range of –1 to +1, with 0 representing no
skill.
recasts, and could be converted to positive skill simply
by replacing all the yes forecasts with no and vice-versa.
TSS is expressed as:
()
TSS ad bc  (18)
() ( )acbd
HSS is the number correct or the
The “standard forecast” is usually the number correct by
ch
proportion correct.
ance or the proportion correct by chance. The range of
the HSS is –∞ to 1. Negative values indicate that the
chance forecast is better, 0 means no skill, and a perfect
forecast obtains a HSS of 1. HSS is expressed as:
2( )
HSS [()() ()()]
ad bc
accd abbd

 (19)
Where “a” is the number of times that for
matched with observed “Yes”, “b” is the number of
of the
Observed
ecast “Yes”
times that forecast “Yes” did not match with observation,
“c” is the number of times that forecast is “No” but ob-
servation is “Yes” and “d” is the number of times that
forecast “No” matched with the observation “No”.
Table 2. Contingency table for computation of skill
arameters. p
YesNo
Yes a b a + b
Forecast
No c + d
a + c b + d
c d
n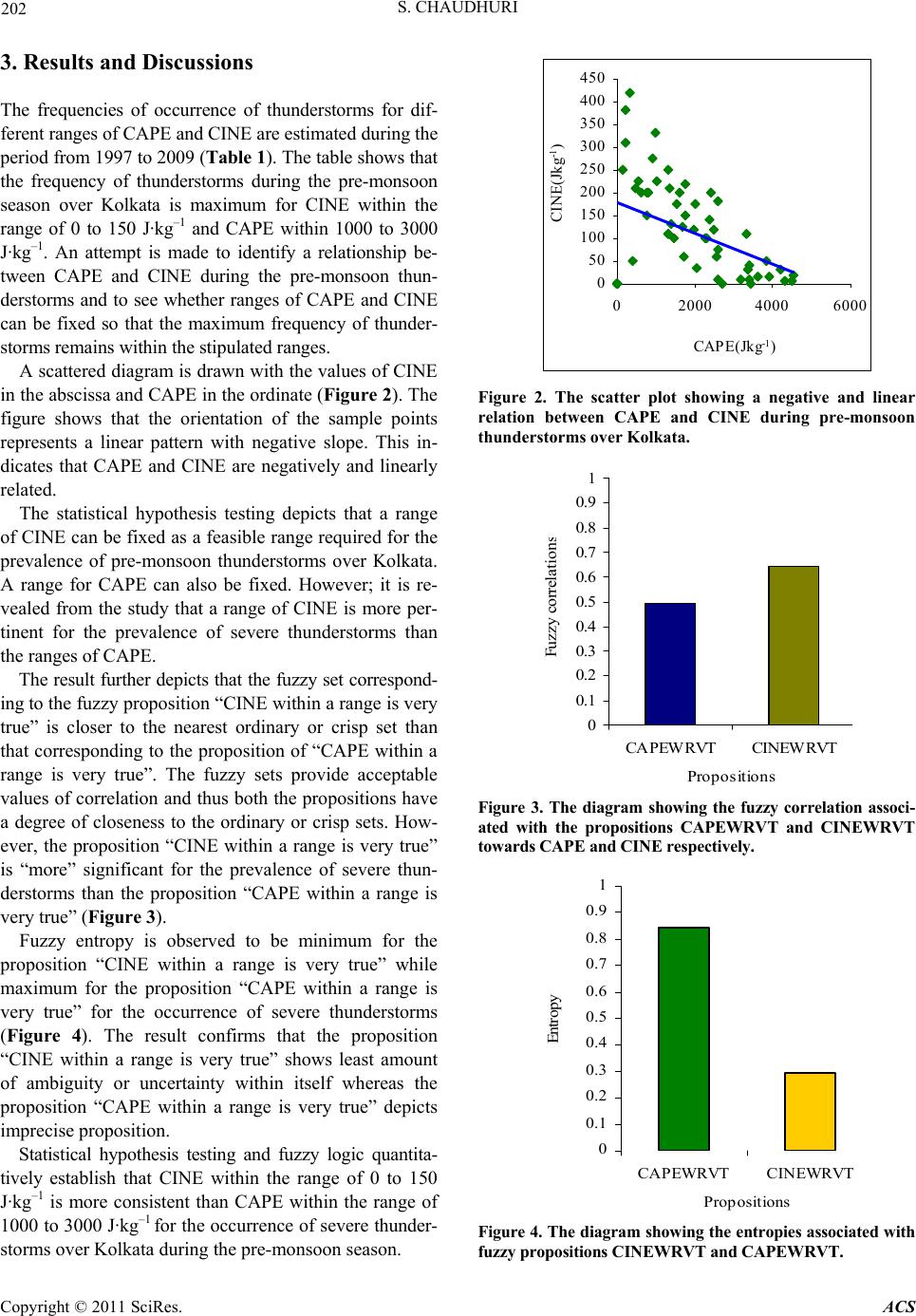

S. CHAUDHURI
202
3. Results and Discussions
thunderstorms for dif-
re estimated during the
The frequencies of occurrence of
ferent ranges of CAPE and CINE a
period from 1997 to 2009 (Table 1). The table shows that
the frequency of thunderstorms during the pre-monsoon
season over Kolkata is maximum for CINE within the
range of 0 to 150 J·kg–1 and CAPE within 1000 to 3000
J·kg–1. An attempt is made to identify a relationship be-
tween CAPE and CINE during the pre-monsoon thun-
derstorms and to see whether ranges of CAPE and CINE
can be fixed so that the maximum frequency of thunder-
storms remains within the stipulated ranges.
A scattered diagram is drawn with the values of CINE
in the abscissa and CAPE in the ordinate (Figure 2). The
figure shows that the orientation of the sample points
represents a linear pattern with negative slope. This in-
dicates that CAPE and CINE are negatively and linearly
related.
The statistical hypothesis testing depicts that a range
of CINE can be fixed as a feasible range required for the
prevalence of pre-monsoon thunderstorms over Kolkata.
A range for CAPE can also be fixed. However; it is re-
vealed from the study that a range of CINE is more per-
tinent for the prevalence of severe thunderstorms than
the ranges of CAPE.
The result further depicts that the fuzzy set correspond-
ing to the fuzzy proposition “CINE within a range is very
true” is closer to the nearest ordinary or crisp set than
that corresponding to the proposition of “CAPE within a
range is very true”. The fuzzy sets provide acceptable
values of correlation and thus both the propositions have
a degree of closeness to the ordinary or crisp sets. How-
ever, the proposition “CINE within a range is very true”
is “more” significant for the prevalence of severe thun-
derstorms than the proposition “CAPE within a range is
very true” (Figure 3).
Fuzzy entropy is observed to be minimum for the
proposition “CINE within a range is very true” while
maximum for the proposition “CAPE within a range is
very true” for the occurrence of severe thunderstorms
(Figure 4). The result confirms that the proposition
“CINE within a range is very true” shows least amount
of ambiguity or uncertainty within itself whereas the
proposition “CAPE within a range is very true” depicts
imprecise proposition.
Statistical hypothesis testing and fuzzy logic quantita-
tively establish that CINE within the range of 0 to 150
J· –1 kg is more consistent than CAPE within the range of
1000 to 3000 J·kg–1 for the occurrence of severe thunder-
storms over Kolkata during the pre-monsoon season.
0
50
100
150
200
250
300
350
400
450
02000 40006000
CAPE(Jkg-1)
CINE(Jkg-1 )
Figure 2. The scatter plot showing a negative and linear
relation between CAPE and CINE during pre-monsoon
thunderstorms ov er Ko lkata.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
s
CAPEWRVT CINEWRVT
Propositions
Fuzzy correlation
Figure 3. The diagram showing the fuzzy correlation associ-
ated with the propositions CAPEWRVT and CINEWRVT
towards CAPE and CINE respectively.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
CAPEWRVT CINEWRVT
Pro
p
ositions
Entropy
Figure 4. The diagram showing the entropies associated with
fuzzy p ropositions CINEWRVT and CAPEWRVT.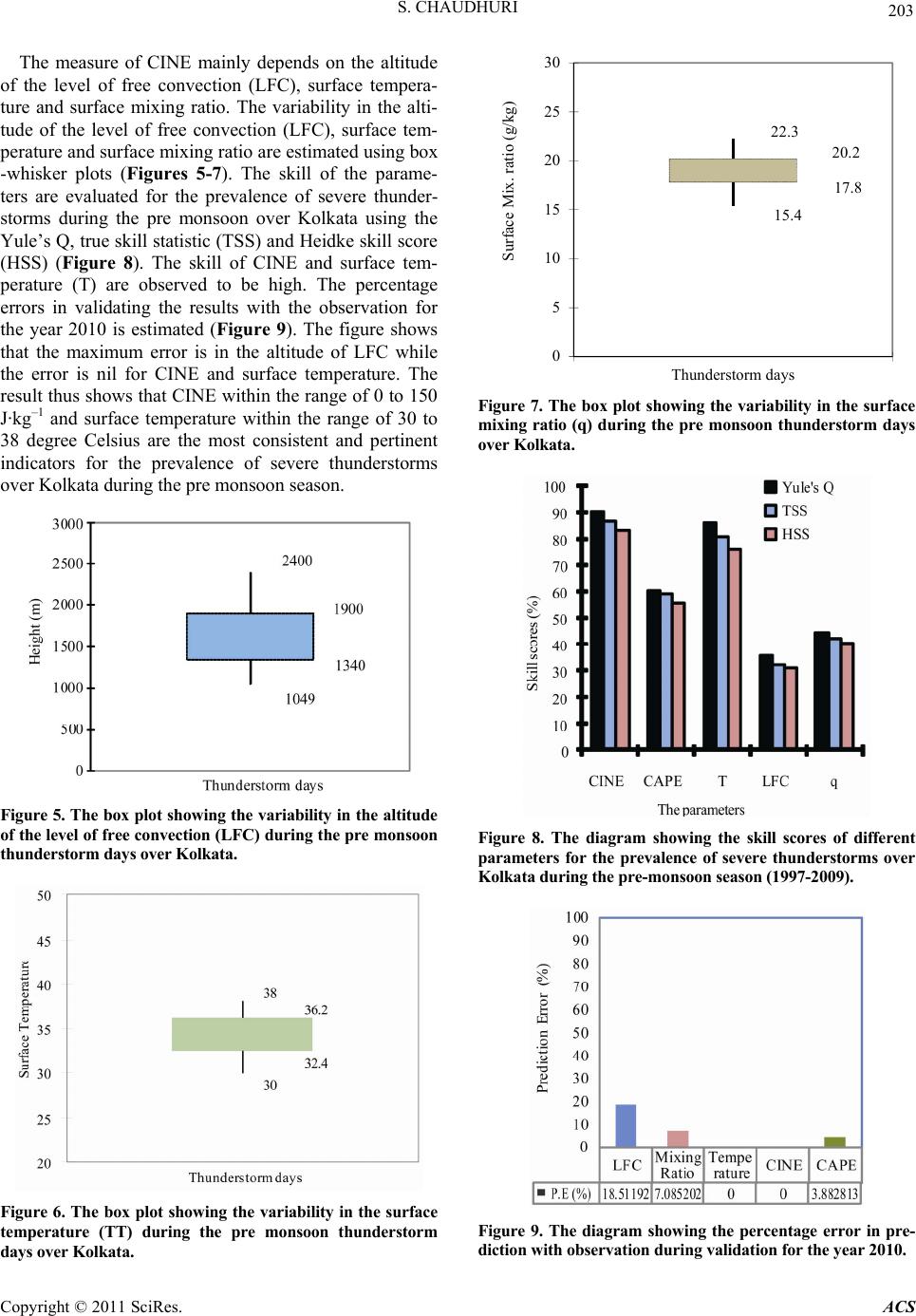

S. CHAUDHURI 203
The measure of CINE mainly depends on the altitude
of the level of free convection (LFC), surface tempera-
ture and surface mixing ratio. The variability in the alti-
tude of the level of free convection (LFC), surface tem-
perature and surface mixing ratio are estimated using box
-whisker plots (Figures 5-7). The skill of the parame-
ters are evaluated for the prevalence of severe thunder-
storms during the pre monsoon over Kolkata using the
Yule’s Q, true skill statistic (TSS) and Heidke skill score
(HSS) (Figure 8). The skill of CINE and surface tem-
perature (T) are observed to be high. The percentage
errors in validating the results with the observation for
the year 2010 is estimated (Figure 9). The figure shows
that the maximum error is in the altitude of LFC while
the error is nil for CINE and surface temperature. The
result thus shows that CINE within the range of 0 to 150
J·kg–1 and surface temperature within the range of 30 to
38 degree Celsius are the most consistent and pertinent
indicators for the prevalence of severe thunderstorms
over Kolkata during the pre monsoon season.
Figure 5. The box plot showing the variability in the altitude
of the level of free convection (LFC) during the pre monsoon
thunderstorm days over Kolkata.
Figure 6. The box plot showing the variability in the surface
temperature (TT) during the pre monsoon thunderstorm
days over Kolkat a.
20.2
22.3
15.4
17.8
0
5
10
15
20
25
30
Thunderstorm days
Surface Mix. ratio (g/kg)
Figure 7. The box plot showing the variability in the surface
mixing ratio (q) during the pre monsoon thunderstorm days
over Kolkata.
Figure 8. The diagram showing the skill scores of different
arameters for thp
Kolka e prevalence of severe thunderstorms over ta during the pre-monsoon season (1997-2009).
Figure 9. The diagram showing the percentage error in pre-
diction with observation during validation for the year 2010.

S. CHAUDHURI
204
he present study leads to conclusion that CINE with
the range of 0 to 150 J·kg–1 and surface temperature
within the range of 30˚C to 38˚C are the most signifycant
parameters for the prevalence of severe thunderstorms
over Kolkata during the pre-monsoon season. It can t
be suggested that if CINE remains within the range 0 -
150 J·kg–1 and surface temperature (T) is within the range
of 30˚C to 38˚C then a warming can be provided for the
prevalence of severe thunderstorms. If the upper ai
tures also support then definite forecast is possible.
5. Acknowledgements
The author acknowledges India Meteorological Depa
ment for sharing the data required for the study. The au-
6. References
of
Society, Vol. 71, 1948, pp.
eophysics, Vol. 5, 1954, pp. 243-248.
y, “On the Subtropical Jet Stream and
evelopment of Large-Scale Convection,”
Tellus, Vol. 8, No. 1, 1956, pp. 26-60.
4. Conclusions
Tin
hus
r fea-
rt-
thor also thanks Urmi Chaudhuri for her serene coop-
eration.
[1] C. W. B. Normand, “Wet Bulb Temperature and Thermo-
dynamics of Air,” Indian Meteorological Memoirs, Vol.
23, Part-I, 1921, pp. 5-11.
[2] IMD, “Nor’westers of West Bengal,” India Meteorological
Department Tech, Note 10, 1941.
[3] H. R. Byers and R. R Jr. Braham, “The Thunderstorm,” U.
S. Government Printing Office, Washington D. C., 1949,
p. 287.
[4] S. Mull and Y. P. Rao, “Effect of Vertical Accele
erstorms,” Quarterly Journal
ration
on Pressure during Thund
the Royal Meteorological
419-421.
[5] B. N. Desai and Y. P. Rao, “On the Cold Pools and Their
Role in the Development of Nor’westers over West Ben-
gal and East Pakistan,” Indian Journal of Meteorology
and G
[6] C. Ramaswam
Role in the D
Its
doi:10.1111/j.2153-3490.1956.tb01194.x
[7] P. Koteswaram and V. Srinivasan, “Thunderstorms over
Gangetic West Bengal in the Pre-Monsoon Season and
Geophysics, Vol. 10,
oting of Cb,” Indian Journal of Meteorology and
orms at Calcutta,” International Journal of
the Synoptic Factors Favorable for Their Formation,” In-
dian Journal of Meteorology and
1958, pp. 275-282.
[8] A. K. Mukherjee and A. K. Chowdhury, “Excessive
Oversho
Geophysics, Vol. 30, 1979, pp. 485-492.
[9] S. Ghosh, P. K. Sen and U. K. De, “Identification of Sig-
nificant Parameters for the Prediction of Pre-Monsoon
Thunderst
Climatology, Vol. 19, No. 6, 1999, pp. 673-681.
doi:10.1002/(SICI)1097-0088(199905)19:6<673::AID-JO
C384>3.0.CO;2-O
[10] S. Chaudhuri, “Identification of the Level of Downdraft
29.
Formation during Severe Thunderstorms: A Frequency
Domain Analysis,” Meteorology and Atmospheric Phys-
ics, Vol. 102, No. 1-2, 2008a, pp. 123-1
doi:10.1007/s00703-008-0014-3
[11] S. Chatterjee, S. Ghosh and U. K. De, “Reduction of
Number of Parameters and Forecasting Convective De-
velopment over Kolkata (22.53˚ N, 88.33˚ E), India dur-
ing Pre-Monsoon Season: An Application of Multivariate
Technique,” Indian Journal of Radio Space Physics&,
ingh and M. Mahakur,
Vol. 38, 2009, pp. 275-282.
[12] S. Chaudhuri and M. Biswas, “Pattern of Meteorological
Parameters during Severe Thunderstorms―A Frequency
Domain Analysis,” Mausam, Vol. 60, No. 1, 2008, pp.
1-10.
[13] P. Chatterjee, D. Pradhan and U. K. De, “Simulation of
Local Severe Storm by Mesoscale Model MM5,” Indian
Journal of Radio & Space Physics, Vol. 37, 2008, pp.
419-433.
[14] A. J. Litta and U. C. Mohanty, “Simulation of a Severe
Thunderstorm Event during the Field Experiment of
STORM Programme 2006, Using WRF-NMM Model,”
Current Science, Vol. 95, No. 2, 2008, pp. 204-215.
[15] P. Mukhopadhyay, H. A. K. S
“The Interaction of Large Scale and Mesoscale Environ-
ment Leading to Formation of Intense Thunderstorms
over Kolkata. Part I: Doppler Radar and Satellite Obser-
vations,” Journal of Earth System Science, Vol. 118, No.
5, 2009, pp. 441-466. doi:10.1007/s12040-009-0046-1
[16] L. A. Zadeh, “Probability Measures of Fuzzy Events,”
Journal of Mathematical Analysis and Applications, Vol.
23, No. 2, 1965, pp. 421-427.
doi:10.1016/0022-247X(68)90078-4
[17] D. W. McCann, “A Neural Network Short-Term Forecast
of Significant Thunderstorms,” Weather and Forecasting,
Vol. 7, No. 3, 1992, pp. 525-534.
doi:10.1175/1520-0434(1992)007<0525:ANNSTF>2.0.C
O;2
[18] C. Marzban and G. Stumpf, “A Neural Networks for
Damaging Wind Prediction,” Weather and Forecasting,
Vol. 13, No. 1, 1998, pp. 151-163.
doi:10.1175/1520-0434(1998)013<0151:ANNFDW>2.0.
CO;2
[19] W. W. Hsieh and T. Tang, “Applying Neural Network
Models to Prediction and Data Analysis in Meteorology
and Oceanography,” Bulletin of the American Meteoro-
logical Society, Vol. 79, No. 9, 1998, pp. 1855-1869.
doi:10.1175/1520-0477(1998)079<1855:ANNMTP>2.0.
CO;2
[20] D. A. K. Fernando and A. W. Jayawardena, “Runoff
Forecasting Using RBF Networks with OLS Algorithm,”
Journal of Hydrologic Engineering, Vol. 3, No
pp. 203-209.
. 3, 1998,
doi:10.1061/(ASCE)1084-0699(1998)3:3(203)
[21] A. S. Elshorbagy, P. Simonovic and U. S. Panu, “Per-
formance Evaluation of Artificial Neural Networks for

S. CHAUDHURI
205
, Vol. 5, No. 4, 2000, pp. 424-427.
Runoff Prediction,” Journal of Hydrologic Engineering
ASCE
doi:10.1061/(ASCE)1084-0699(2000)5:4(424)
[22] A. S. Tokar and M. Markus, “Precipitation-Runoff Mod-
eling Using Artificial Neural Netw
Models,” Journal of Hydrologic Engineering, Vol. 5, No.
2, 2000
orks and Conceptu
, pp. 156-161.
al
doi:10.1061/(ASCE)1084-0699(2000)5:2(156)
[23] C. Marzban and A. Witt, “A Bayesian Neural Network
for Severe Hail Size Prediction,” Weather and Forecast-
ing, Vol. 16, No. 5, 2001, pp. 600-610.
doi:10.1175/1520-0434(2001)016<0600:ABNNFS>2.0.C
O;2
[24] A. Abraham, N. S. Philip and B. Joseph, “Will We Have
a Wet Summer? Long Term Rain Forecasting Using Soft
Computing Models,” In: E. J. H. Kerchoffs and M.
Snorek, eds., Modeling and Simulation 2001, Pu
of the Society for Computer Simulation Inteblication rnational,
, Vol. 285,
Prague, 2001, pp. 1044-1048.
[25] M. P. Rajurkar , U. C. Kothyari and U. C. Chaube, “Mod-
eling of the Daily Rainfall-Runoff Relationship with Ar-
tificial Neural Network,” Journal of Hydrology
No. 1-4, 2001, pp. 96-113.
doi:10.1016/j.jhydrol.2003.08.011
[26] L. Jin, C. Yao and Y. K. Huang, “A Nonlinear Artificial
Intelligence Ensemble Prediction Model for Typhoon In-
tensity,” Monthly Weather Review, Vol. 136,
2008, pp. 4541-4554.
No. 12,
69.1doi:10.1175/2008MWR22
ology, Vol. 25, No. 7, 2008, pp. 1136-1148.
[27] Y. Wang, T. Y. Yu, M. Yeary, A. Shapiro, S. Nemati, M.
Foster, D. L. Jr Andra and M. Jain, “Tornado Detection
Using a Neuro-Fuzzy System to Integrate Shear and Spec-
tral Signatures,” Journal of Atmospheric and Oceanic
Techn
doi:10.1175/2007JTECHA1022.1
[28] S. Chaudhuri, “Genetic Algorithm to Recognize Apt En-
ergy for the Genesis of Severe Thunderstorms,” Vatabaran,
AFAC Journal of Meteorology, Vol. 29, No. 2, 2008, pp.
1-8.
S. Chaudhuri, “Ampliative Rea[29] soning to View the Preva-
lence of Severe Thunderstorms,” Mausam-Quarterly
Journal of Meteorology, Hydrology & Geophysics, Vol.
57, No. 3, 2006, pp. 523-526.
[30] S. Chaudhuri, “Artificial Neural Ne
cast Maximum Wind Speed Associa
twork Model to Fore-
ted with Severe Thun-
derstorms,” Vatabaran, AFAC Journal of Meteorology,
Vol. 30, No. 1, 2006, pp. 14-19.
[31] S. Chaudhuri, “A Hybrid Model to Estimate the Depth of
Potential Convective Instability during Severe Thunder-
storms,” Soft Computing, Vol. 10, No. 8, 2006, pp. 643-
648. doi:10.1007/s00500-005-0532-6
[32] S. Chaudhuri and S. Aich Bhowmik, “CAPE―A Link
between Thermodynamics and Microphysics for the Oc-
currence of Severe Thunderstorms,” Mausam-Quarterly
Journal of Meteorology, Hydrology & Geophysics, Vol.
57, No. 2, 2006, pp. 249-254.
[33] S. Chaudhuri, “Chaotic Graph Theory Approach for
Identification of Convective Available Potential Energy
(CAPE) Patterns Required for the Genesis of Severe
Thunderstorms,” Advances in Complex Systems, Vol. 10,
No. 3, 2007, pp. 413-422.
doi:10.1142/S0219525907001215
[34] S. Chaudhuri, “Consequences of Surface Parameters due
to the Occurrence of Severe Thunderstorms―A View
through Rough Set Theory,” Science & Culture, Vol. 73,
No. 11-12, 2007, pp. 391-395.
[35] S. Chaudhuri, “Preferred Type of Cloud in the Genesis of
Severe Thunderstorms―A Soft Computing Approach,”
Atmospheric Research, Vol. 88, No. 2, 2008, pp. 149-156.
doi:10.1016/j.atmosres.2007.10.008
[36] S. Chaudhuri and A. Middey, “The Applicability of Bi-
partite Graph Model for Thunderstorm Forecast over
Kolkata,” Advances in Meteorology, Vol. 2009, 2009, pp.
1-12. doi:10.1155/2009/270530
[37] S. Chaudhuri, “Convective Energies in Forecasting Se-
vere Thunderstorms with One Hidden Layer Neural Net
and Variable Learning Rate Back Propagation Algo-
rithm,” Asia-Pacific Journal of Atmospheric Sciences,
Vol. 46, No. 2, 2010, pp. 173-183.
[38] S. Chaudhuri, “Predictability of Severe Thunderstorms
with Fractal Dimension Approach,” Asian Journal of Wa-
ter, Air & Environmental Pollution, Vol. 7, No. 4, 2010,
pp. 81-87.
[39] S. Chaudhuri and A. Middey, “Nowcasting Thunder-
storms with Graph Spectral Distance and Entropy Esti-
mation,” Meteorological Applications, Vol. 18, No. 2,
2011, pp. 238-249. doi:10.1002/met.240
[40] D. S. Wilks, “Statistical Methods in the Atmospheric
ns, Chichester, 2003.
Sciences,” 2nd Edition, Elsevier, Oxford, 2006.
[41] I. T. Jolliffe and D. B. Stephenson, “Forecast Verification:
A Practitioner’s Guide in Atmospheric Science,” John
Wiley and So
[42] D. S. Wilks, “Statistical Methods in Atmospheric Sci-
ences,” Academic Press, Cambridge, 1995, pp. 114-122.