Paper Menu >>
Journal Menu >>
 New Journal of Glass and Ceramics, 2011, 1, 112-118 doi:10.4236/njgc.2011.13016 Published Online October 2011 (http://www.SciRP.org/journal/njgc) Copyright © 2011 SciRes. NJGC Effect of AgI on Conduction Mechanism in Silver-Vanadate Superionic Glasses Poonam Sharma, D. K. Kanchan*, Meenakshi Pant, Manish S. Jayswal, Nirali Gondaliya Solid Sate Ionics & Glass Research Laboratory, Department of Physics, Faculty of Science, The M.S. University of Baroda, Vado- dara (Gujarat), India. Email: *d_k_kanchan@yahoo.com Received June 14th, 2011; revised July 27th, 2011; accepted August 9th, 2011. ABSTRACT A quaternary super-ionic glass system xAgI: (95-x) [Ag2O:2V2O5]: 5TeO2, where 40 ≤ x ≤ 65 in steps of 5, has been pre- pared by melt quenching technique. The prepared glass samples are characterized by X-ray, FTIR and DSC studies. As revealed by the FTIR spectra, the oxyanion network is not affected by the addition of AgI. The frequency dependence of the electrical conductivity for various glass compositions at different temperatures has been analyzed in terms of Jon- scher’s universal power law. The measurements reveal that the conductivity increases from σ = 7.62 × 10–7 S/cm to 1.15 × 10–4 S/cm with increasing AgI content. The temperature dependent conductivity obeys the Arrhenius relationship. The impedance and modulus studies indicate the non-debye type of the frequency dispersion for all the glass samples. Keywords: Conductivity, Glass Transition Temperature, Infrared Spectra, Impedance, Modulus 1. Introduction AgI and Ag oxysalt based ion conducting materials at- tracted much attention from last many years, because of their high ionic conductivity at room temperature [1-4]. The glasses formed by AgI and Ag oxysalt complexes are constituted by randomly oriented micro domains ma- de by arrays of tetrahedral oxysalt complexes [5]. These complexes are linked together and are surrounded by non- mobile Ag+ ions which coordinate iodide polyhedra con- taining mobile Ag+ ions. The conductivity maximum is realized when the oxyanions are coordinated with the largest number of iodide polyhedral which is compatible with the vitreous state. In general, it is found that the ionic conductivity increases with the AgI content in the glass composition. Although AgI based glasses have been studied widely, very limited studies have been re- ported on silver-based vanado-tellurite glasses [6]. Hence, we have used V2O5and TeO2 as two glass formers with a very low amount of TeO2 salt (only 5 wt %) as it is dif- ficult to obtain glasses with high V2O5 contents and small amount of TeO2 is reported to induce superionic behavior when it is doped with metal halide [7]. Montani et. al. [8] had shown that addition of the Ag2O (network modifier) to the electronic V2O5 and TeO2 glass results the block- ing of the electronic paths which causes the electronic conductivity to fall down. And increasing network modi- fier concentration gives rise to more ionic transport due to closeness of non-bridging oxygens. The objective of present work is to investigate the in- fluence of AgI salt content on conduction mechanism and ionic relaxation behavior in Ag2O-V2O5 -TeO2 glass system in framework of the modulus formalism i.e., the conductivity relaxation mechanism. In order to view this effect, we have prepared xAgI - (95-x)[Ag2O:2V2O5] - 5TeO2 glass system, where 40 ≤ x≤ 65 in steps of 5 in the present paper. 2. Experimental Analytical Reagent grade starting chemicals: AgI, Ag2O, V2O5 and TeO2 were used to prepare the samples. All the compositions were weighed according to their mol%, crushed and then ground in an agate mortar and pestle for 2 hours by wet grinding method. The homogenous mix- ture obtained was then kept in an alumina crucible in a controlled electric muffle furnace at 673K. Subsequently, the furnace was heated to 673K at a rate of 100K/h and the melt was kept for 4 h at that temperature. After 4 hours, the melt was poured on a heavy thick copper plate kept at room temperature and pressed by another similar copper plate to quench it. X-ray diffraction was carried by X-ray diffraction ana- lyzer (Shimadzu) at 20 / min scan rate to confirm the amor- phous nature of prepared glass samples. The glass transi- tion temperature of the amorphous samples was measured 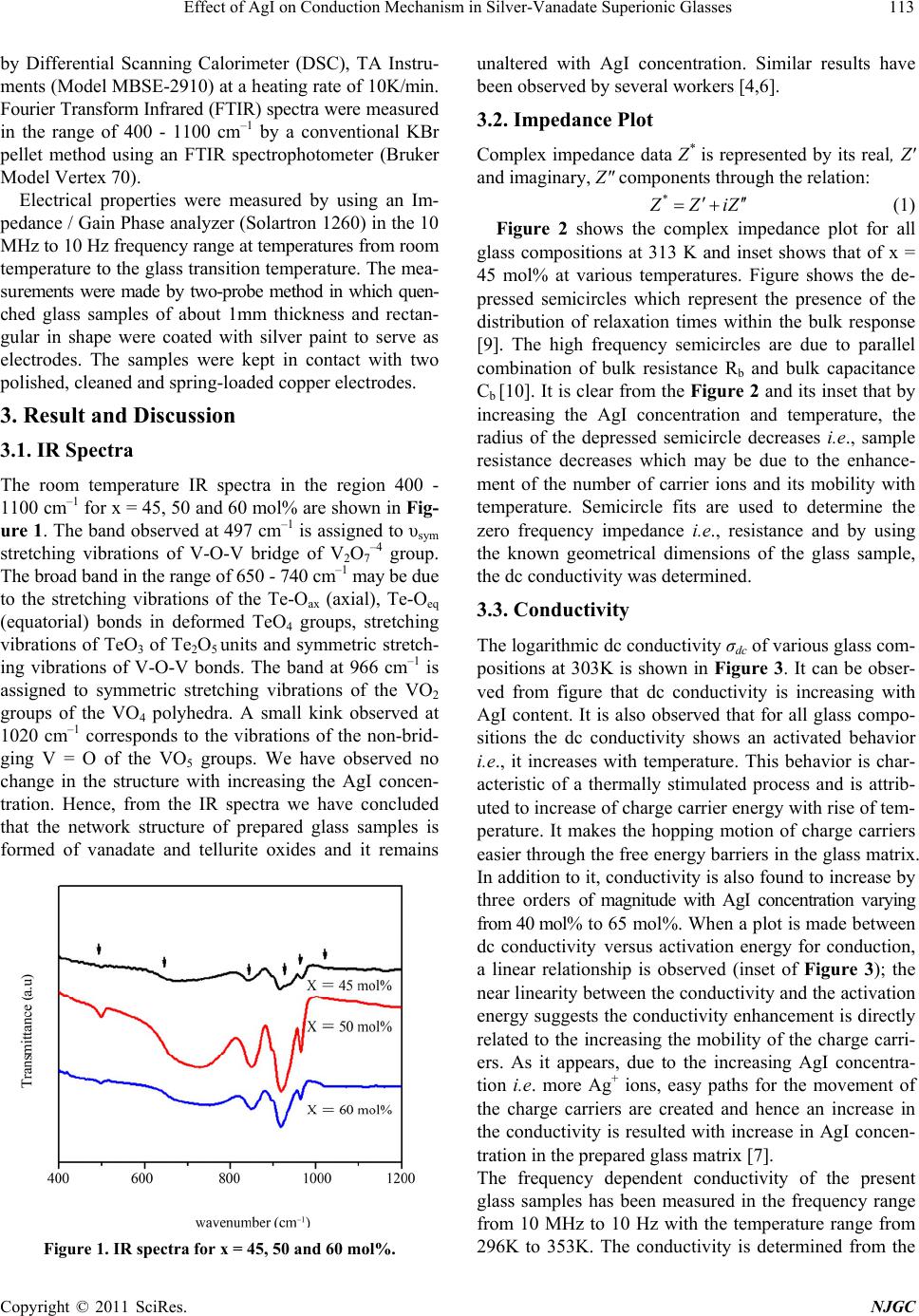 Effect of AgI on Conduction Mechanism in Silver-Vanadate Superionic Glasses113 by Differential Scanning Calorimeter (DSC), TA Instru- ments (Model MBSE-2910) at a heating rate of 10K/min. Fourier Transform Infrared (FTIR) spectra were measured in the range of 400 - 1100 cm–1 by a conventional KBr pellet method using an FTIR spectrophotometer (Bruker Model Vertex 70). Electrical properties were measured by using an Im- pedance / Gain Phase analyzer (Solartron 1260) in the 10 MHz to 10 Hz frequency range at temperatures from room temperature to the glass transition temperature. The mea- surements were made by two-probe method in which quen- ched glass samples of about 1mm thickness and rectan- gular in shape were coated with silver paint to serve as electrodes. The samples were kept in contact with two polished, cleaned and spring-loaded copper electrodes. 3. Result and Discussion 3.1. IR Spectra The room temperature IR spectra in the region 400 - 1100 cm–1 for x = 45, 50 and 60 mol% are shown in Fig- ure 1. The band observed at 497 cm–1 is assigned to υsym stretching vibrations of V-O-V bridge of V2O7 –4 group. The broad band in the range of 650 - 740 cm–1 may be due to the stretching vibrations of the Te-Oax (axial), Te-Oeq (equatorial) bonds in deformed TeO4 groups, stretching vibrations of TeO3 of Te2O5 units and symmetric stretch- ing vibrations of V-O-V bonds. The band at 966 cm–1 is assigned to symmetric stretching vibrations of the VO2 groups of the VO4 polyhedra. A small kink observed at 1020 cm–1 corresponds to the vibrations of the non-brid- ging V = O of the VO5 groups. We have observed no change in the structure with increasing the AgI concen- tration. Hence, from the IR spectra we have concluded that the network structure of prepared glass samples is formed of vanadate and tellurite oxides and it remains Figure 1. IR spectra for x = 45, 50 and 60 mol%. unaltered with AgI concentration. Similar results have been observed by several workers [4,6]. 3.2. Impedance Plot Complex impedance data Z* is represented by its real, Z' and imaginary, Z″ components through the relation: * Z ZiZ (1) Figure 2 shows the complex impedance plot for all glass compositions at 313 K and inset shows that of x = 45 mol% at various temperatures. Figure shows the de- pressed semicircles which represent the presence of the distribution of relaxation times within the bulk response [9]. The high frequency semicircles are due to parallel combination of bulk resistance Rb and bulk capacitance Cb [10]. It is clear from the Figure 2 and its inset that by increasing the AgI concentration and temperature, the radius of the depressed semicircle decreases i.e., sample resistance decreases which may be due to the enhance- ment of the number of carrier ions and its mobility with temperature. Semicircle fits are used to determine the zero frequency impedance i.e., resistance and by using the known geometrical dimensions of the glass sample, the dc conductivity was determined. 3.3. Conductivity The logarithmic dc conductivity σdc of various glass com- positions at 303K is shown in Figure 3. It can be obser- ved from figure that dc conductivity is increasing with AgI content. It is also observed that for all glass compo- sitions the dc conductivity shows an activated behavior i.e., it increases with temperature. This behavior is char- acteristic of a thermally stimulated process and is attrib- uted to increase of charge carrier energy with rise of tem- perature. It makes the hopping motion of charge carriers easier through the free energy barriers in the glass matrix. In addition to it, conductivity is also found to increase by three orders of magnitude with AgI concentration varying from 40 mol% to 65 mol%. When a plot is made between dc conductivity versus activation energy for conduction, a linear relationship is observed (inset of Figure 3); the near linearity between the conductivity and the activation energy suggests the conductivity enhancement is directly related to the increasing the mobility of the charge carri- ers. As it appears, due to the increasing AgI concentra- tion i.e. more Ag+ ions, easy paths for the movement of the charge carriers are created and hence an increase in the conductivity is resulted with increase in AgI concen- tration in the prepared glass matrix [7]. The frequency dependent conductivity of the present glass samples has been measured in the frequency range from 10 MHz to 10 Hz with the temperature range from 296K to 353K. The conductivity is determined from the Copyright © 2011 SciRes. NJGC 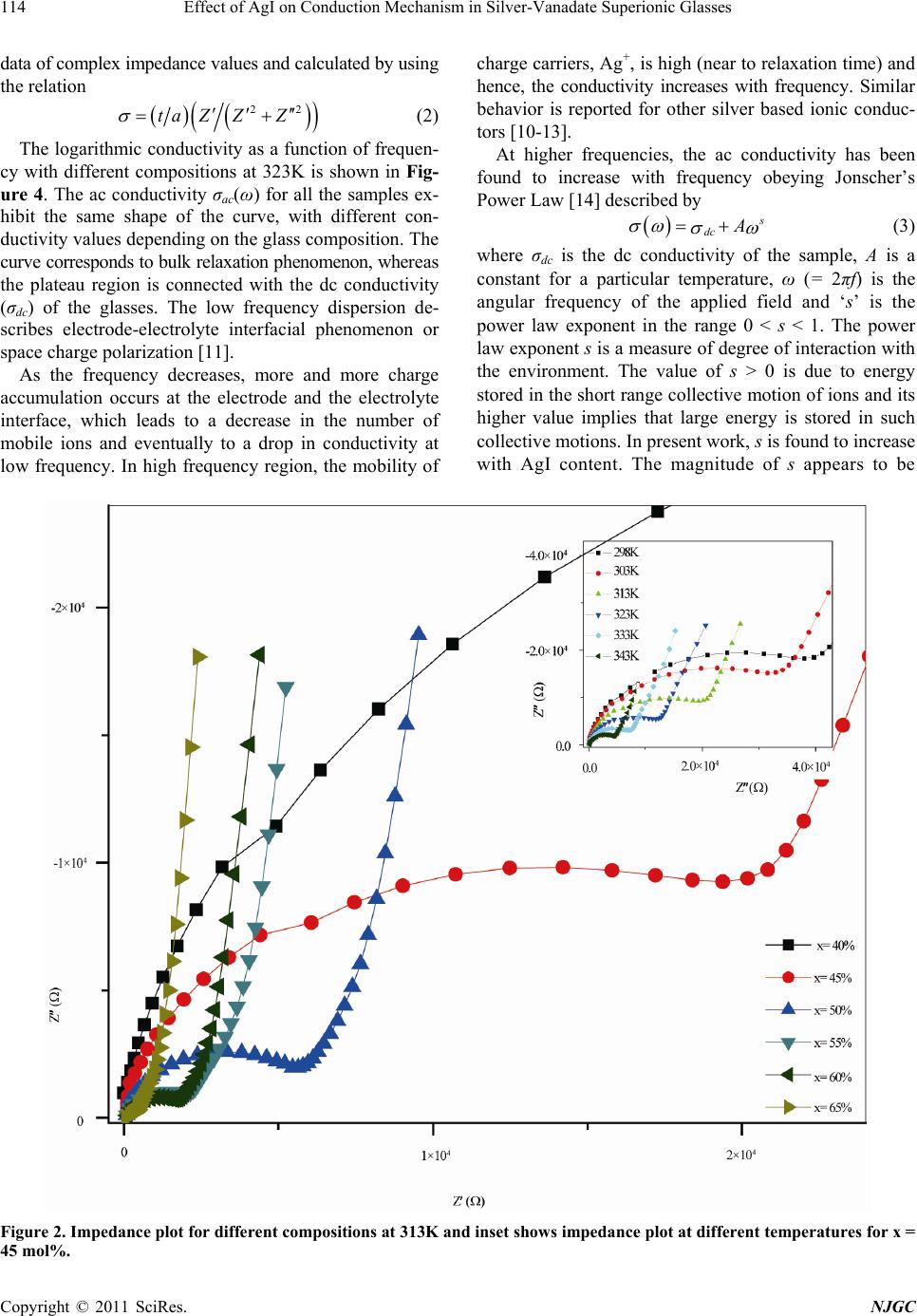 Effect of AgI on Conduction Mechanism in Silver-Vanadate Superionic Glasses Copyright © 2011 SciRes. NJGC 114 data of complex impedance values and calculated by using the relation 2 2 ta ZZZ (2) The logarithmic conductivity as a function of frequen- cy with different compositions at 323K is shown in Fig- ure 4. The ac conductivity σac(ω) for all the samples ex- hibit the same shape of the curve, with different con- ductivity values depending on the glass composition. The curve corresponds to bulk relaxation phenomenon, whereas the plateau region is connected with the dc conductivity (σdc) of the glasses. The low frequency dispersion de- scribes electrode-electrolyte interfacial phenomenon or space charge polarization [11]. As the frequency decreases, more and more charge accumulation occurs at the electrode and the electrolyte interface, which leads to a decrease in the number of mobile ions and eventually to a drop in conductivity at low frequency. In high frequency region, the mobility of charge carriers, Ag+, is high (near to relaxation time) and hence, the conductivity increases with frequency. Similar behavior is reported for other silver based ionic conduc- tors [10-13]. At higher frequencies, the ac conductivity has been found to increase with frequency obeying Jonscher’s Power Law [14] described by s dc A (3) where σdc is the dc conductivity of the sample, A is a constant for a particular temperature, ω (= 2πf) is the angular frequency of the applied field and ‘s’ is the power law exponent in the range 0 < s < 1. The power law exponent s is a measure of degree of interaction with the environment. The value of s > 0 is due to energy stored in the short range collective motion of ions and its higher value implies that large energy is stored in such collective motions. In present work, s is found to increase with AgI content. The magnitude of s appears to be Figure 2. Impedance plot for different co mpositions at 313K and inset shows impedance plot at different temperatures for x = 45 mol%. 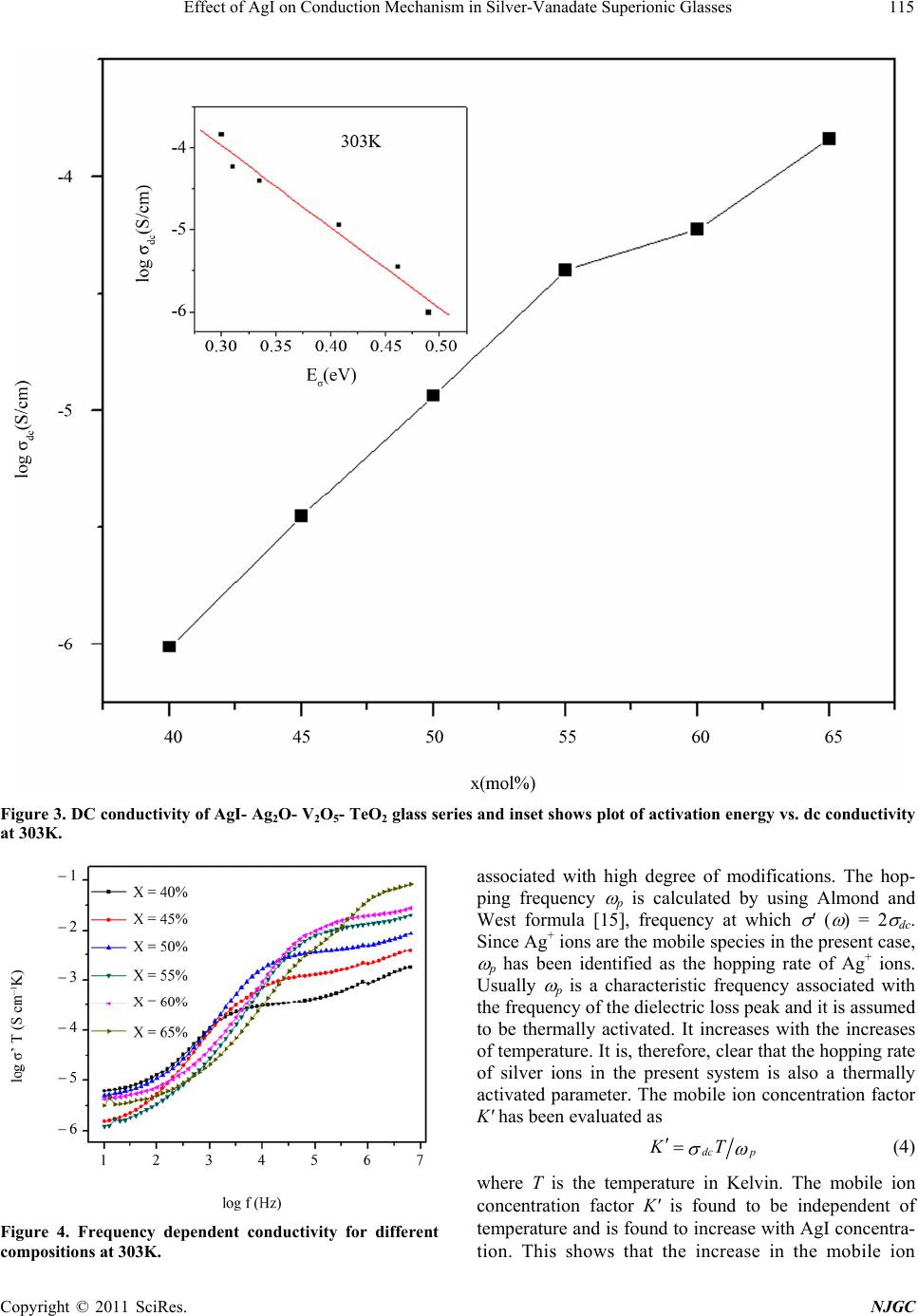 Effect of AgI on Conduction Mechanism in Silver-Vanadate Superionic Glasses115 Figure 3. DC conductivity of AgI- Ag2O- V2O5- TeO2 glass series and inset show s plot of activation ene rgy vs. dc c onductivity at 303K. Figure 4. Frequency dependent conductivity for different compositions at 303K. associated with high degree of modifications. The hop- ping frequency p is calculated by using Almond and West formula [15], frequency at which ′ ( ) = 2 dc. Since Ag+ ions are the mobile species in the present case, p has been identified as the hopping rate of Ag+ ions. Usually p is a characteristic frequency associated with the frequency of the dielectric loss peak and it is assumed to be thermally activated. It increases with the increases of temperature. It is, therefore, clear that the hopping rate of silver ions in the present system is also a thermally activated parameter. The mobile ion concentration factor K' has been evaluated as dc p KT (4) where T is the temperature in Kelvin. The mobile ion concentration factor K' is found to be independent of temperature and is found to increase with AgI concentra- tion. This shows that the increase in the mobile ion Copyright © 2011 SciRes. NJGC  Effect of AgI on Conduction Mechanism in Silver-Vanadate Superionic Glasses 116 concentration is attributed to the increase in the conduc- tivity i.e; with the increase in the AgI content. 3.4. Modulus Formalism Modulus spectroscopy highlights the bulk effects and it is complementary to impedance spectroscopy which high- lights electrode and grain-boundary effects. This forma- lism is particularly suitable to detect phenomena as elec- trode polarization and bulk property such as average re- laxation time [16,17]. We have used the complex electric modulus formalism to analyze the relaxation processes in the present system as it discriminates against electrode polarization and other interfacial effects. Electric modu- lus can be represented by the following equation. * 0 jC * M Z (5) In an ideal solid electrolyte system, it can be repre- sented by a single parallel RC element, where R and C represent the resistance and capacitance, respectively and is characterized by a single time constant as conductivity relaxation time. In ideal system, the peak maximum of Z″ and M″ is found at the same frequency and the shape of the peaks are identical with that predicted by Debye the- ory [18]. With the appropriate scaling, the normalized- modulus and impedance spectra of the Debye curves are completely superposable and are given by the equation: 2 1 RC ZR RC ; 0 2 1 CRC MCRC (6) The term, ωRC /[1+(ωRC)2 ] in imaginary part of im- pedance, Z″ and imaginary part of modulus, M″ is re- sponsible for debye-like peak shapes. To understand the non-debye behavior of the prepared glass samples, Z″ and M″ at 303K have been plotted in Figure 5 for x = 60 mol% glass sample. It is observed from figure that the Z″max and M″max do not occur at the same frequency which indicate a wide distribution of relaxation times. At low frequencies, Z″ shows large rise due to electrode 02468 0.0 -2.0x106 -4.0x106 -6.0x106 -8.0x106 Z" M" log f Z" 0.000 0.005 0.010 0.015 0.020 M" Figure 5. The impedance and modulus spectrum for x = 40mol% at 303K. polarization and at high frequency broadened modulus spectra indicates the distribution of relaxation times [19]. The real and imaginary part of modulus spectra for x = 45 mol% at different temperatures is presented in Figure 6 (a) and Figure 6 (b) respectively. Other glasses also showed almost similar M′ and M″ temperature depend- ence behavior. From M′ graph, it shows that whatever be the temperature, the value of M′( ) reaches a constant value at higher frequencies. At low frequencies, M′ and M″ approaches to zero indicating that the electrode po- larization phenomenon make a negligible contribution to M* and may be ignored when the electric data has been analyzed in this form [20]. The observed long tail at low frequencies is due to the large capacitance associated with the electrodes. The M″( ) spectrum relative to a given temperature shows an asymmetrical peak approximately centered in the dispersion region of M′( ). The asymmetrical peaks obtained suggest that the material can be interpreted by an equivalent circuit composed of a single parallel RC element [18]. The left part of the peak corresponds to 234567 -4.0 -3.5 -3.0 -2.5 -2.0 -1.5 -1.0 296K 303K 313K 323K 333K 343K 353K log M' log f (Hz) (a) (a) 1234567 0.000 0.006 0.012 0.018 296K 303K 313K 323K 333K 343K 353K M" log f (Hz) (b) (b) Figure 6. Frequenc y dependence of (a) re al part, M′ and (b) imaginary part of modulus, M″ at different temperatures for x = 45mol%. Copyright © 2011 SciRes. NJGC  Effect of AgI on Conduction Mechanism in Silver-Vanadate Superionic Glasses117 long range mobility and the right part of the peak is at- tributed to ions spatially confined in narrow potential wells. The frequency range where the peak occurs indi- cates the transition between long and short range mobil- ity and is defined by the condition c c = 1 [21] where c is the most probable relaxation time of ions. The M″ ( ) peak height is found to be nearly same at different tem- peratures and it is observed to shift to a higher frequency with increasing temperature. The peak in M″ variation corresponds to the relaxation frequency and the corre- sponding relaxation time is systematically shifted to higher frequencies as the temperature increases. Figure 7 shows the normalized plot of M″ / M″max ver- sus log f / fmax of the modulus for the glassy system for x = 50 mol% at different temperatures. The approximate over- lap of the modulus curves for all temperatures indicates the dynamical processes occurring at different frequent- cies are independent of temperature. Such results were also observed for other glass compositions. It is found that the normalized plot for different compositions do not merge on a single master curve which implies that the conductivity relaxation depends on the glass composition. This has usually been regarded as an indication of a dis- tribution of relaxation times in the conduction process [20].The observed broad peak can be assigned to the sum- mation of relaxations occurring in the bulk materials. The full width at half height obtained is greater than the De- bye type of relaxation with single time constant is attrib- uted to the presence of strong ion-ion interaction. The observed normalized plot is non-symmetric in agreement with the non-exponential behavior of the electrical func- tion described by Kohlrausch-William-Watts (KWW) exponential function [22] exptt ; (7) 10 where and are the conductivity relaxation time and Kohlrausch exponent respectively. The value of the Kohl- rausch parameter for most practical solid electrolyte is Figure 7. Normalized plot of M″ at different temperatures for x = 50mol%. smaller than one. The calculated values of lies in the range of 0.6 - 0.9 that is in agreement with the values reported [23]. 4. Conclusions The ionic conduction of the prepared glasses is a cones- quence of the presence of glass modifier (Ag2O) and the dopant (AgI). IR spectra show that the network structure of prepared glass samples is formed of vanadate and tel- lurite oxides and remains unaltered with AgI concentra- tion. The conductivity is found to obey the universal power law. The ionic conductivity as well as power law exponent is found to increase with AgI concentration. The modulus plot shows non-debye behavior and is asymmetric with respect to the peak maxima. The peaks are considerably broader on both sides of the maxima. The broadened modulus spectrum indicates the distribu- tion of relaxation times in the conduction process. It is inferred from the normalized plot of the prepared glass samples that the conductivity relaxation is independent of temperature but composition dependent. REFERENCES [1] D. Dutta and A. Ghosh, “Dynamics of Ag+ Ions in Binary Tellurite Glasses,” Physical Review E, Vol. 52, No. 2, 2005, pp. 024201-024203. doi:10.1103/PhysRevB.72.024201 [2] K. P. Padmasree and D. K. Kanchan, “Conductivity and Dielectric Studies on 20CdI2-80[xAg2O-y(0.7V2O5- 0.3B2O3) Super Ion Conducting System Where 1x/y3,” Journal of Non-Crystalline Solids, Vol. 352, No. 36-37, 2006, pp. 3841-3848. doi:10.1016/j.jnoncrysol.2006.06.012 [3] J. E. Garbarczyk, P. Machowski, M. Wasiucionek and W. Jakubowski, “Electrical Properties of AgI-Ag2O-V2O5-P2O5 Glasses,” Solid State Ionics, Vol. 157, No. 1-4, 2003, pp. 269-273.doi:10.1016/S0167-2738(02)00220-5 [4] A. K. Arof and S. Radhakrishna, “Electrical Properties of Silver Vanadate Electrochemical Cells,” Journal of Alloys and Compounds, Vol. 200, No. 1-2, 1993, pp. 129-134. doi:10.1016/0925-8388(93)90482-3 [5] T. Minami, “Preparation and Properties of Superionic Conducting Glasses Based on Silver Halides,” Journal of Non-Crystalline Solids, Vol. 56, No. 1-3, 1983, pp. 15-26. doi:10.1016/0022-3093(83)90440-4 [6] M. Pant, D. K. Kanchan, P. Sharma and M. S. Jayswal, “Mixed Conductivity Studies in Silver Oxide Based Bar- ium Vanado-Tellurite Glasses,” Material Science and Engineering B, Vol. 149, No. 1, 2008, pp. 18-25. doi:10.1016/j.mseb.2007.11.037 [7] G. El-Damrawi, “Silver Ion Transporting Mechanism in Superionic Conducting AgI-Ag2O-TeO2,” Journal of Physics: Condensed Matter, Vol. 11, No. 33, 1999, pp. 6385-6394. doi:10.1088/0953-8984/11/33/308 [8] R. A. Montani, A. Lorente and A. M. Frechero, “Effect of Copyright © 2011 SciRes. NJGC  Effect of AgI on Conduction Mechanism in Silver-Vanadate Superionic Glasses Copyright © 2011 SciRes. NJGC 118 Ag2O on the Conductive Behaviour of Silver Vanadium Tellurite Glasses,” Solid State Ionics, Vol. 146, No. 2-3, 2002, pp. 323-327. doi:10.1016/S0167-2738(01)01023-2 [9] J. R. Macdonald, “Impedance Spectroscopy and its Use in Analyzing the Steady State Ac Response of Solid and Liquid Electrolytes,” Journal of Electroanalytical Chem- istry and Interfacial Electrochemistry, Vol. 223, No. 1-2, 1987, pp. 25-50. doi:10.1016/0022-0728(87)85249-X [10] M. Pant, D. K. Kanchan and N. Gondaliya, “Transport Properties and Relaxation Studies in BaO Substituted Ag2O-V2O5-TeO2 Glass System,” Material Chemistry and Physics, Vol. 115, No. 1, 2009, pp. 98-104. doi:10.1016/j.matchemphys.2008.11.047 [11] M. D. Ingram, “Ionic Conductivity in Glass,” Physics and Chemistry of Glasses, Vol. 28, 1987, pp. 215-234. [12] J. Kawamura, S. Rikito, M. Shinya and M. Shimoji, “AC Conductivity of Li2O---Na2O---B2O3 Mixed-Alkali Gla- sses: Analysis Due to Transition Rate Distribution,” Solid State Ionics, Vol. 25, No. 2-3, 1987, pp. 155-164. doi:10.1016/0167-2738(87)90115-9 [13] N. Satyanaryan, A. Karthikeyan and M. Venkateswarlu, “AC Conductivity Studies on the Silver Molybdo-Arsenate Glassy System,” Journal of Material Science, Vol. 31, No. 20, 1996, pp. 5471-5477. doi:10.1007/BF01159319 [14] A. K. Jonscher, “The ‘Universal’ Dielectric Response,” Na- ture, Vol. 267, 1977, pp. 673-679.doi:10.1038/267673a0 [15] D. P. Almond, C. K. Duncan and A. R. West, “The De- termination of Hopping Rates and Carrier Concentrations in Ionic Conductors by a New Analysis of AC Conduc- tivity,” Solid State Ionics, Vol. 8, No. 2, 1983, pp. 159-164. doi:10.1016/0167-2738(83)90079-6 [16] D. P. Almond and A. R. West, “Impedance and Modulus Spectroscopy of Real Dispersive Conductors,” Solid State Ionics, Vol. 11, No. 1, 1983, pp. 57-64. doi:10.1016/0167-2738(83)90063-2 [17] J. M. Reau, X. Y. Jun, J. Senegas, C. L. Deit and M. Pou- lain, “Influence of Network Modifiers on Conductivity and Relaxation Parameters in Some Series of Fluoride Glasses Containing LiF,” Solid State Ionics, Vol. 95, No. 3-4, 1997, pp. 191-197. doi:10.1016/S0167-2738(96)00564-4 [18] R. J. Grant, M. D. Ingram and A. R.West, “An Investiga- tion of -alumina Electrolytes by Electric Modulus Spec- troscopy,” Electrochimica Acta, Vol. 22, No. 7, 1977, pp. 729-734. doi:10.1016/0013-4686(77)80027-3 [19] J. M. Reau, S. Rossignol, B. Tanguy, J. M. Rojo, P. Herrero, R. M. Rojas and J. Sanz, “Conductivity Relaxa- tion Parameters of Some Ag+ Conducting Tellurite Glasses Containing AgI or the (AgI)0.75 (T1I)0.25 Eutectic Mixture,” Solid State Ionics, Vol. 74, No. 1-2, 1994, pp. 65-73. doi:10.1016/0167-2738(94)90438-3 [20] M. Sural, A. Ghosh, “Electric Conductivity and Relaxa- tion in ZnF2–AlF3–PbF2–LiF Glasses,” Solid State Ionics, Vol. 130, No. 3-4, 2000, pp. 259-266. doi:10.1016/S0167-2738(00)00641-X [21] P. B. Macedo, C. T. Moynihan and R. Bose, “The Role of Ionic Diffusion in Polarization in Vitreous Ionic Conduc- tors,” Physics and Chemistry of Glasses, Vol. 13, 1972, pp. 171-179. [22] G. Williams and D. C. Watts, “Non-Symmetrical Dielec- tric Relaxation Behavior Arising from a Simple Empirical Decay Function,” Transactions of the Faraday Society, Vol. 66, 1970, 80-85, doi:10.1039/TF9706600080. [23] A. Pan and A. Ghosh, “Dynamics of Lithium Ions in Bis- muthate Glasses,” Journal of Chemical Physics, Vol. 112, No. 3, 2000, pp. 1503-1509. doi:10.1063/1.480717 |

