Technology and Investment Vol.06 No.01(2015), Article ID:54159,4
pages
10.4236/ti.2015.61008
Bundling and Consumers’ Reservation Value: Effects on Market Entry
Qing Hu
Graduate School of Economics, Kobe University, Kobe, Japan
Email: huqing549@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 December 2014; accepted 13 February 2015; published 16 February 2015
ABSTRACT
We consider a multiproduct incumbent which monopolizes one market but faces a potential entrant in another market. In a two dimensional Hotelling model, when consumers’ reservation value is relatively high, we show that the incumbent has an incentive to use bundling to deter entry only if a prior commitment is applicable. However, when consumers’ reservation value is low, the multiproduct firm even has no incentive to use bundling and bundling has no effect on entry deterrence.
Keywords:
Bundling, Entry Deterrence, Multiproduct firm, Product-Specific Preferences

1. Introduction
Suppose a multiproduct incumbent monopolizes one market but faces a potential entrant in another market. Whinston (1990) considered such a situation and, using a simple Hotelling model, argued that the incumbent could deter entry by bundling but only if it makes a prior commitment [1] . Nalebuff (2004) showed that in a modified Hotelling model, if the incumbent chooses prices before the entrant, it could deter entry by bundling even without any commitment [2] . Peitz (2008) showed that bundling may block entry in a two-dimensional Hotelling model [3] . However, there is a lack of research on this question by considering consumers’ reservation value.
In reality, consumers hold different reservation value to different products. A consumer’s reservation value is the highest price she is willing to pay. A product may be very welcomed thus consumers’ reservation value is very high and consumers are willing to pay high price. One example may be Apple Company’s products, saying IPhone. When the firm launches a new version of IPhone, consumers rush into the store to buy at a high price. At the same time, there are goods that are not popular for consumers, thus many people do not want to afford. We can say that consumers’ reservation value is relatively low in this case. Therefore, it is closer to the reality if we consider the entry deterrence problem by considering consumer’s reservation value. In opposite to previous work [1] - [3] where deterring entry by bundling (monopoly under bundling) is always more profitable than letting the entry occur, we find that when consumer’s reservation value is low, the incumbent even has no incentive to use bundling to deter entry. But when consumer’s reservation value is relatively high, it is not the case.
Bundling has attracted significant research attention, and most studies in this field consider symmetric competition. Matutes and Regibeau (1988) examined the incentive of pure bundling for two symmetric, multiproduct firms by building a two-dimensional Hotelling unit square [4] . They found that pure bundling selling strategies were always dominated by independent pricing strategy, regardless of the level of consumers’ reservation value. Gans and King (2006) extended Matutes and Regibeau’s (1992) model to analyze the incentives associated with mixed bundling [5] [6] . Thanassoulis (2007) and Armstrong and Vickers (2010) analyzed the case of mixed bundling in a fully served market [7] [8] .
The remainder of this paper is arranged as follows. In Section 2, the model is introduced. In Section 3, we analyze equilibriums and results. In Section 4, we present our conclusion.
2. The Model
Suppose there are two products, products 1 and 2. Product 1 is only provided by firm A, while product 2 may also be provided by firm B. We assume the marginal cost of either product for both firms is zero. Firm A has two strategies to select from, that is, pure bundling and independent pricing. Consumers purchase at most one unit of each product. Therefore, consumers are able to select at most six consumption combinations if firm A does not bundle, namely AA, AB, A1, A2, B2, and purchasing nothing. AA means buying products 1 and 2 from firm A; AB means buying product 1 from firm A and product 2 from firm B; and A1, A2, and B2 mean purchasing only a single product 1 from firm A, a single product 2 from firm A, and a single product 2 from firm B, respectively. A consumer purchasing one product will have a reservation value of C. Therefore, a consumer will have 2C if she purchases two products. We engage in a three-stage game. At the first stage, firm B decides whether to enter. If it enters, it pays a cost of F. At the second stage, firm A decides whether to bundle. At stage three, firms simultaneously set prices. We consider four situations: (1) independent pricing by monopolist A, (2) bundling by monopolist A, (3) competitive independent pricing, and (4) competitive bundling.
Consumers should be uniformly located in a Hotelling unit square with firm A located
at (0, 0) and firm B located at (1, 1). The horizontal interval represents product
1 and as a consumer located further away from firm A horizontally, she holds less
taste preference towards firm A’s product 1 and more prefers to firm B’s product
1. The vertical interval represents product 2. Under an independent pricing scheme,
a consumer located at
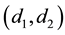
buying AB will get a surplus of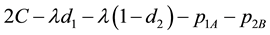 , where
, where
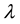 is the strength parameter of differentiation. Similarly, the consumer purchasing
only a single product will get a surplus
is the strength parameter of differentiation. Similarly, the consumer purchasing
only a single product will get a surplus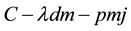 ,
,
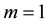 , 2,
, 2,
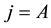 , B. When firm
A bundles, the consumer buying the bundle will earn a surplus
, B. When firm
A bundles, the consumer buying the bundle will earn a surplus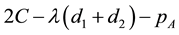 , where
, where
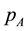 is the bundle price.
is the bundle price.
We denote the profit of firms A and B as ,
,
 , respectively.
, respectively.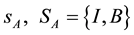 , where I
, where I
stands for independent pricing and B stands for bundling. In addition,
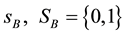 , where 0 means
does not enter and 1 means enter.
, where 0 means
does not enter and 1 means enter.
3. The Equilibrium Prices and Results
We extend the model of Matutes and Regibeau (1988) [4] by adding the single consumption.
For simplicity of calculation, we set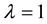 . We show the market configurations according to different levels
of consumers’ reservation value
. We show the market configurations according to different levels
of consumers’ reservation value
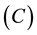 in Figure 1. Concerning the situation where firm
A bundles in a competitive market (situation 4), we demonstrate an example for the
calculation in the situation where
in Figure 1. Concerning the situation where firm
A bundles in a competitive market (situation 4), we demonstrate an example for the
calculation in the situation where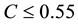 . The demand of AA on the horizontal and vertical axes are the
same, and we denote demand as
. The demand of AA on the horizontal and vertical axes are the
same, and we denote demand as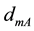 ,
,

(i.e.,




Independent pricing selling by a monopolist A





(a)(C < 2) (C ≥ 2)Bundling by a monopolist A (b)(C < 0.75) (C ≥ 0.75)Competitive independent pricing (c)(C < 1) (when 1 ≤ C < 1.5, adjacent market. (C ≥ 2)when 1.5 ≤ C < 2, competitive market)Competitive bundling (d)(C < 0.55) (0.55 ≤ C < 0.8) (0.8 ≤ C < 1.3) (e)(1.3 ≤ C < 2) (C ≥ 2)
Figure 1. Market configurations.
When







When












We find if firm A monopolizes the market, when




We can easily see if

However, if
We can see if

In a monopoly market, the bundle price is always lower than the total price of the
two products under independent pricing. However, when consumers’ reservation value
is small, consumers who cannot buy the bundle can buy single product under independent
pricing. Independent pricing provides more selections and the demand under this
situation is larger. Thus


4. Conclusion
When
Table 1. Firm A and Firm B’s profits when C = 0.6.
Table 2. Firm A and Firm B’s profits when C = 1.4.
which are not that popular for consumers so that there are many consumers that even do not want or just want one rather than both, we see that bundling cannot deter entry. If the products are very welcomed, bundling may deter entry only if the incumbent makes a prior commit. Therefore, we can see that by considering consumers’ reservation value in a two dimensional Hotelling model, bundling is not easy to happen because prior commitment to bundling is also difficult sometimes.
References
- Whinston, M. (1990) Tying, Foreclosure, and Exclusion. American Economic Review, 80, 837-860.
- Nalebuff, B. (2004) Bundling as an Entry Barrier. Quarterly Journal of Economics, 119, 159-187. http://dx.doi.org/10.1162/003355304772839551
- Peitz., M. (2008) Bundling May Blockade Entry. International Journal of Industrial Organization, 26, 41-58. http://dx.doi.org/10.1016/j.ijindorg.2006.09.005
- Matutes, C. and Regibeau, P. (1988) “Mix and Match”: Product Compatibility without Network Externalities. The RAND Journal of Economics, 19, 221-234. http://dx.doi.org/10.2307/2555701
- Gans, J.S. and King, S.P. (2005) Paying for Loyalty: Product Bundling in Oligopoly. Journal of Industrial Economics, 54, 43-62.
- Matutes, C., and Regibeau, P. (1992) Compatibility and Bundling of Complementary Goods in a Duopoly. Journal of Industrial Economics, 40, 37-54. http://dx.doi.org/10.2307/2950626
- Thanassoulis, J. (2007) Competitive Mixed Bundling and Consumer Surplus. Journal of Economics & Management Strategy, 16, 437-467. http://dx.doi.org/10.1111/j.1530-9134.2007.00145.x
- Armstrong, M. and Vickers, J. (2010) Competitive Nonlinear Pricing and Bundling. The Review of Economic Studies, 77, 30-60. http://dx.doi.org/10.1111/j.1467-937X.2009.00562.x
Appendix
Because there are a great number of market configurations and the ways of calculations are similar, we show one example of how we derived the outcomes. For more calculations, please contact with the author for the calculation paper.
When









The Equations of (A) and (B) can be solved by computer for several values of



