Technology and Investment
Vol.2 No.3(2011), Article ID:7017,6 pages DOI:10.4236/ti.2011.23023
Banking Firm, Risk of Investment and Derivatives
1Department of Business and Economics, Technische Universität Dresden, Dresden, Germany
2Department of Economics, Hong Kong Baptist University, Hong Kong, China
E-mail: udo.broll@tu-dresden.de, awong@hkbu.edu.hk
Received September 13, 2010; revised May 17, 2011; accepted May 24, 2011
Keywords: banking firm, investment, risk, derivatives, hedging, (µ, s)-preferences, stochastic dominance
Abstract
The economic environment for financial institutions has become increasingly risky. Hence these institutions must find ways to manage risk of which one of the most important forms is credit risk. In this paper we use the mean-variance (mean-standard deviation) approach to examine a banking firm investing in risky assets and hedging opportunities. The mean-standard deviation framework can be used because our hedging model satisfies a scale and location condition. The focus of this study is on how credit risk affects optimal bank investment in the loan and deposit market when derivatives are available. Furthermore we explore the relationship among the firstand second-degree stochastic dominance efficient sets and the mean-variance efficient set.
1. Introduction
In our paper we examine the behavior of a banking firm under credit risk. The banking firm can hedge its investment risk exposure by trading futures contracts. Credit risk is one of the most important forms of risk faced by banks as financial intermediaries. Management of risk through the selection and monitoring of borrowers and creating diversified loan portfolios has always been one of the predominant challenges in risk management in the banking sector [1,2].
In our model we will use the term derivatives for both securities originating from loan securitization and financial advanced instruments such as futures and options. One of our objectives is to examine how the possibility of selling part of the entire uncertain loan portfolio of a bank at a deterministic forward rate will affect the bank’s behavior in the deposit and loan market. Derivatives are financial instruments designed to reduce interest rate risk.
Derivatives can take the form of forwards, options or swaps which may be imbedded in financial assets such as loans and bonds. Derivatives allow an investor to reduce or eliminate credit risk or to buy credit risk in order to control total risk.
The number of derivatives transactions has increased significantly worldwide in recent years. The main reason for the rise of derivatives is an increase in dramatically fluctuations in risk as in the Asian Financial Crises in 1997, the Russian Financial Crises 1998, the Argentinean Financial Crisis in 2001, Enron crisis in 2002 and the financial crisis in 2007. There are many ways in which financial managers can utilize derivatives. The main applications are hedging, arbitrage and speculation. This paper shall focus on hedging, i.e., the desire of an investor to reduce risks in order to stabilize income and cashflow streams.
The basic motivation of the study can be interpreted as follows. Banks face risk. If the banking firm does not hedge, there will be some stochastic variability in the cashflows. Random fluctuations in cashflows due to credit risk result in variability in the amount of the bank’s profits. Variability in profits will generally be undesirable, to the extent that there is risk aversion. As derivatives have the ability to reduce this variability in cashflows, consequently the expected utility of the bank manager can be increased [3,4].
This study analyzes the optimal hedging policy of a risk-averse competitive banking firm faced with an exogenous change in credit risk. The two-dimensional meanstandard deviation model are used because this approach provides a clear and straightforward economic intuition for the bank’s revision of its optimal hedging policy whenever a parameter of the decision-making process changes. [5-7] have shown that if all random alternatives to be ranked are equal in distribution to one another, with the exception of scale and location, then any expected utility ranking of all random alternatives can be based solely on the means and standard deviations of the alternatives. Many well-known families of distribution functions, including the bank hedging model presented in this paper, satisfy this location and scale condition.
The analysis in this paper is based on the concept of (µ, σ)-preferences. The (µ, σ)-criterion on decision-making under uncertainty has experienced growing attention in very recent contributions, see for example, [8-13]. For a (µ, σ) risk-averse bank manager, this study derives a direct relationship between an exogenous change in parameters, the optimal hedge ratio and the elasticity of risk aversion. Furthermore, the relationship between the firstand second-degree stochastic dominance efficient sets and the mean-variance efficient set are explored.
The plan of the paper is as follows. Section 2 presents the model of a competitive banking firm under credit risk when derivatives are available. Derivation of the main results will be included. In Section 3 the concept of stochastic dominance is introduced to explore the relationship between the firstand second-degree stochastic dominance efficient sets and the mean-variance efficient set. Section 4 will be the conclusion.
2. Optimal Hedging and Increase in Risk
Consider a risk-averse bank in a one period framework. The bank is a financial intermediary, taking deposits D and making loans L. By bank’s technology it faces operational costs C(L, D) with strictly positive marginal costs: 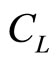 > 0 and
> 0 and 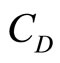 > 0. Equity capital, K, of the bank is assumed to be as given. At the beginning of the period, the bank has the following balance sheet:
> 0. Equity capital, K, of the bank is assumed to be as given. At the beginning of the period, the bank has the following balance sheet:
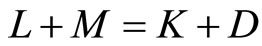
where M is the bank’s interbank market position. M can take a positive or a negative sign, implying lending or borrowing in the interbank market at an interest rate r which is assumed to be deterministic.
Loans, L, granted by the bank are risky subjected to uncentain repayment. Therefore the effective rate of return is risky:
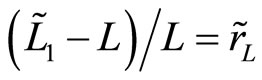
Deposits issued by the bank is assumed to have the same maturity as the loans. The bank is a quantity setter in the loan and deposit market where the supply of deposits is perfectly elastic and the deposit rate, 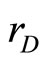 , is given. With credit risk, the random profit of the bank is defined as
, is given. With credit risk, the random profit of the bank is defined as
 .
.
Profits consist of the uncertain interest earned on loans plus positive (negative) interest on interbank position minus interest rate paid on deposits and operational costs.
As highlighted in the literature, there are many new instruments in the financial markets today which allow efficient risk management in banking. The creation of such instruments to manage credit risk is one of the most important steps towards complete risk-sharing markets. The following section shall analyze the impact of derivatives on a bank’s optimal deposit, loan decisions and risk management. The derivative trades a risky cashflow into a certain cashflow. The bank can hedge the credit risk by taking a short (long) position, i.e., selling (buying) contracts H, in the derivatives market. The given forward rate is denoted by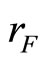 . It is assumed that there is a positive risk premium in the futures market (backwardation), i.e.
. It is assumed that there is a positive risk premium in the futures market (backwardation), i.e. .
.
Substituting the bank’s balance constraint and taking into account hedging possibilities will lead to
 .
.
The bank management is (m, s)-risk averse. This means that (i) the agent’s preference can be represented by a two-parameter function V(m, s) defined over mean m and standard deviation s of the underlying random variable, Y, such that:

where u is the utility function, Y is an investment or return with mean m, standard deviation s and pdf fY and (ii) that the function V satisfies the following properties: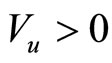 ,
,  ,
, 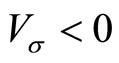 ,
, 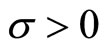 and
and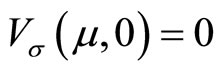 . Assume that the partial derivatives
. Assume that the partial derivatives 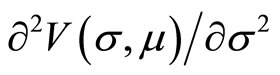 and
and  exist, then V is a strictly concave function and the indifference curves are convex in the (s, m)-space [14].
exist, then V is a strictly concave function and the indifference curves are convex in the (s, m)-space [14].
Given (s, m)-risk aversion, the decision problem of the bank management reads:
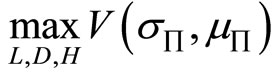 where
where 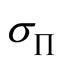 and
and 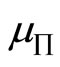 are expected profit and the standard deviation of profit respectively. Examination of the first order necessary conditions for the maximization problem leads to the following proposition:
are expected profit and the standard deviation of profit respectively. Examination of the first order necessary conditions for the maximization problem leads to the following proposition:
Proposition 1: Given an derivative market and the bank’s exposure to credit risk as described above, in the optimum: bank can separate its decision on risk management from its decisions on loan and deposit volumes and with backwardation, the bank underhedges its credit risk exposure.
Proof: From the first order conditions, we obtain two deterministic equations in loans L and deposits D such that:
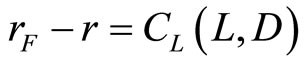 ,
,
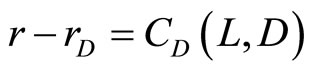 .
.
Since the derivative market is biased, we have 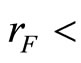
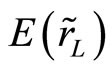 , an underhedge, i.e. L < H, is then implied.
, an underhedge, i.e. L < H, is then implied.
Proposition 1 is an example of the well-known separation property in the presence of hedging instrument. As a consequence, the bank will choose a volume of loans and deposits as in the case of certainty. Furthermore Proposition 1 is the result of the biasedness, i.e., a risk premium leads to an underhedged position.
The elasticity of risk aversion can be derived by characterizing the sensitivity of the hedge against a change in risk. In order to analyze an increase in risk and the revision of the optimal hedge policy, H, the elasticity of risk aversion is defined as follows:
Definition 1: Given s > 0, the elasticity of risk aversion with respect to the standard deviation is
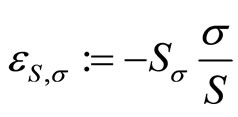
where  and
and .
.
Let S be the marginal rate of substitution between m and s, thus, S is interpreted as a measure of risk aversion in the (s, m)-space. The elasticity of risk aversion,  , is—in absolute value—given by the percentage change in risk aversion divided by the percentage change in risk.
, is—in absolute value—given by the percentage change in risk aversion divided by the percentage change in risk.
The change in credit risk is as follows: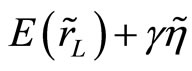
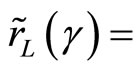 , where
, where 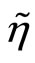 has zero mean and unit standard deviation. Then, increasing
has zero mean and unit standard deviation. Then, increasing 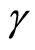 models an increase in risk. Substituting
models an increase in risk. Substituting 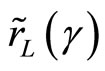 for the random variable generates a relationship between optimal hedge amount
for the random variable generates a relationship between optimal hedge amount 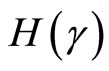 and the risk measured by the standard deviation of
and the risk measured by the standard deviation of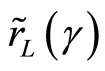 . Now the following claim can be made.
. Now the following claim can be made.
Proposition 2: Given backwardation in the derivatives market, when the risk increases, then the optimal hedge will increase if the elasticity of risk aversion is less than unity; remains unchanged if the elasticity of risk aversion is unity.
Proof: Expected profit and standard deviation of profit are respectively

By using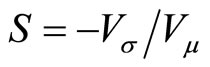 , the first order condition of the hedge problem implies
, the first order condition of the hedge problem implies
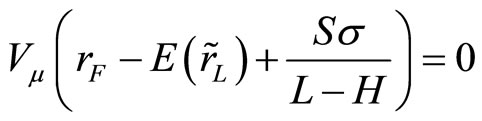 .
.
This condition can be satisfied if and only if the term in brackets equals to zero. Applying the implicit function theorem and Definition 1, we have:
sign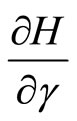 = sign
= sign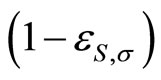 .
.
Definition 2: Given s > 0, the elasticity of risk aversion with respect to the expected profit wealth is:
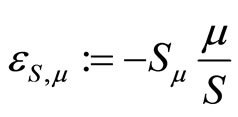
where 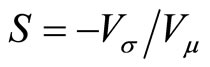 and
and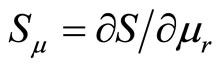 .
.
Corollary 1: With an increase in the expected futures rate, 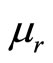 , the hedge ratio will decrease if the elasticity of risk aversion is less than unity; remain unchanged if the elasticity of risk aversion is unity; and increases if the elasticity of risk aversion is greater than unity.
, the hedge ratio will decrease if the elasticity of risk aversion is less than unity; remain unchanged if the elasticity of risk aversion is unity; and increases if the elasticity of risk aversion is greater than unity.
Proof: Using the same calculus as in proof of proposition 2 one can easily verify that sign = sign
= sign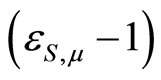 .
.
3. Stochastic Dominance and Mean-Variance Approach
Mean-variance efficient sets have been widely used in both economics and finance to analyze how people make their choices among risky assets. [15] demonstrated that if the ordering of alternatives is to satisfy the NM (Von Neumann-Morgenstern, [16]) axioms of rational behavior, only a quadratic NM utility function is consistent with an ordinal expected utility function that depends solely on the mean and variance of the return. Thereafter, [17] formulated an efficient set of definitions corresponding to the quadratic utility assumption. [18] pointed out that even if the return for each alternative has a normal distribution, the mean-variance framework cannot be used to rank alternatives consistent with the NM axioms unless a quadratic utility function is used.
[7] extended the mean-variance theory to include the comparison among distributions that differ only by location and scale parameters and to include general utility functions with only convexity or concavity restrictions. [19] elaborated on Meyer’s results to prove that the firstand second-degree stochastic dominance efficient sets are equal to the mean-variance efficient set under certain conditions while [20] found that the sign changes of the indifference curve slope depend on the speed of increase in the absolute risk aversion.
Earlier on, this paper has used the mean-variance (or mean-standard deviation) approach to examine a banking firm that is subjected to certain credit risk and hedging opportunities for a scale and location family of distributions. Next, it shall explore the linkage of the mean-variance efficient set to both the firstand second-degree stochastic dominance efficient sets and to the utility functions for both non-satiated and risk-averse investors. Definition of the stochastic dominance concept is as follows:
Definition 3: Given two random variables X and Y with F and G as their respective probability distribution functions, X is at least as large as Y and F is at least as large as G is the sense of:
1) FSD, denoted by  or
or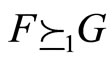 , if and only if
, if and only if 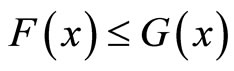 for each x;
for each x;
2) SSD, denoted by 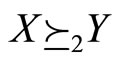 or
or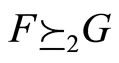 , if and only if
, if and only if 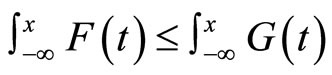 for each x;
for each x;
where FSD and SSD stand for first and second order stochastic dominance respectively. If in addition there exists x such that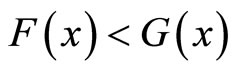 and
and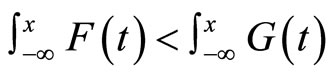 , we say that X is larger than Y and F is larger than G in the second of SFSD and SSSD, denoted by
, we say that X is larger than Y and F is larger than G in the second of SFSD and SSSD, denoted by 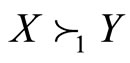 or
or 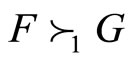 and
and  or
or 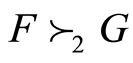 respectively, where SFSD and SSSD stand for strictly first and second order stochastic dominance respectively. The definitions of the utility functions for both non-satiated and risk-averse investors are as follow:
respectively, where SFSD and SSSD stand for strictly first and second order stochastic dominance respectively. The definitions of the utility functions for both non-satiated and risk-averse investors are as follow:
Definition 4:
1) For n = 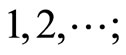
 and
and 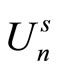 are sets of utility functions u such that:
are sets of utility functions u such that:

where 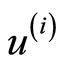 is the
is the 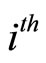 derivative of the utility function u.
derivative of the utility function u.
2) The extended sets of utility functions are defined as follows:
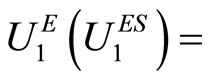 {u: u is (strictly) increasing}and
{u: u is (strictly) increasing}and
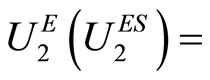 {u is increasing and (strictly) concave}.
{u is increasing and (strictly) concave}.
Note that in Definition 4, it is known (e.g. see Theorem 11C in [21]) that u in  are differentiable almost everywhere and their derivatives are continuous almost everywhere. Notice that any investor whose utility function belongs to
are differentiable almost everywhere and their derivatives are continuous almost everywhere. Notice that any investor whose utility function belongs to 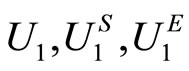 or
or  is a nonsatiated investor who prefers more to less. Any investor whose utility function belongs to
is a nonsatiated investor who prefers more to less. Any investor whose utility function belongs to 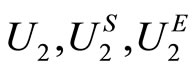 or
or  is a non-satiated and risk-averse investor who prefers more to less but whose marginal utility function is decreasing. The relationship between the investment distributions with stochastic dominance relation and the utility function of the non-satiated and risk-averse investors have been well developed as summarized in the following proposition:
is a non-satiated and risk-averse investor who prefers more to less but whose marginal utility function is decreasing. The relationship between the investment distributions with stochastic dominance relation and the utility function of the non-satiated and risk-averse investors have been well developed as summarized in the following proposition:
Proposition 3: Let X and Y be random variables with probability distribution functions F and G respectively. Suppose u is a utility function. For n = 1 and 2; we have the following:  if and only if
if and only if 
 for any u in U such that
for any u in U such that
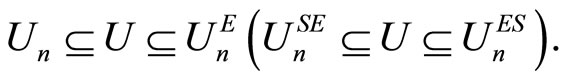
Note that Definition 4 holds for any integer n and Definition 3 and Proposition 3 hold for the third order for Proposition 3 can be found in [22]. The third order is excluded in this paper because only the results in the first two orders are needed. The proof for Proposition 3 can be found in [6,16,23-25]. [10] extended Proposition 3 to include the convex stochastic dominance theory.
The basic principle underlying stochastic dominance is quite straightforward. As an example, suppose that investors attempt to choose between two risky assets, X and Y. Also, suppose that the distribution of returns to assets X and Y are highly complicated, but the return to asset X always exceeds the return to asset Y. In this case, as long as investors are non-satiated, no one will buy asset Y since the investors can always do better by holding asset X. This basically iterates the results of the above proposition with n = 1. Similarly, the above proposition with n = 2 demonstrates that the non-satiated and risk-averse investors will prefer risky asset X to Y if and only if X stochastically dominates Y in the second order. As Proposition 3 provides the equivalent relationship between stochastic dominance and utility function, a person is thus known as a first order stochastic dominance (FSD) risk investor (or known as a non-satiated investor) if his/her utility function belongs to  and call a person a second order stochastic dominance (SSD) risk averter (or called as a non-satiated and risk-averse investor) if his/her utility function belongs to
and call a person a second order stochastic dominance (SSD) risk averter (or called as a non-satiated and risk-averse investor) if his/her utility function belongs to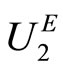 . The preference of random profits in a location-scale family of distributions for the FSD and SSD investors are further explored in the following proposition:
. The preference of random profits in a location-scale family of distributions for the FSD and SSD investors are further explored in the following proposition:
Proposition 4: For the random profits 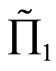 and
and 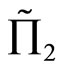 with means
with means  and
and  respectively such that
respectively such that
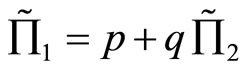
1) if 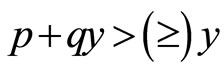 for all y, then
for all y, then  for any u such that
for any u such that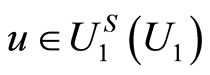 ; and
; and
2) if 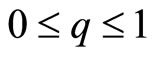 such that
such that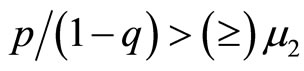 , i.e.,
, i.e., 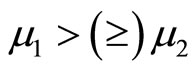 , then
, then 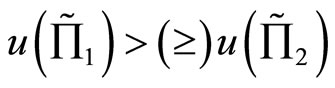 for any
for any 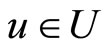 such that
such that
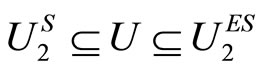 .
.
Proof: For part (1),
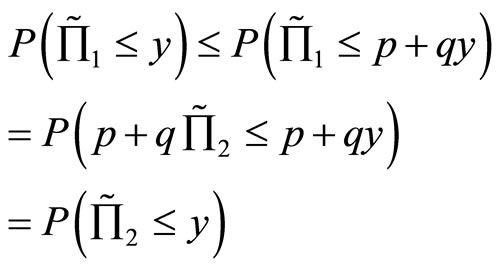
Hence, . Together with the results in Proposition 3, we obtain part (1). One can easily modify the proof in [24] to obtain the proof of part (2).
. Together with the results in Proposition 3, we obtain part (1). One can easily modify the proof in [24] to obtain the proof of part (2).
Proposition 4 illustrates that if two random profits belong to the same location-scale family satisfying 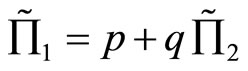 with
with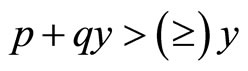 , then the random profit
, then the random profit  stochastically dominates the random profit
stochastically dominates the random profit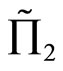 . Hence the random profit
. Hence the random profit 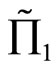 is preferred by FSD investors. The random profits satisfying the inequality relationship as stated in part (2) of Proposition 4, then
is preferred by FSD investors. The random profits satisfying the inequality relationship as stated in part (2) of Proposition 4, then 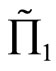 is preferred to
is preferred to 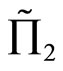 for any SSD investor. These results are also suitable for the effective rates of returns as stated in the following corollary:
for any SSD investor. These results are also suitable for the effective rates of returns as stated in the following corollary:
Corollary 2: For the effective rates of returns 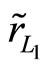 and
and  with means
with means 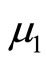 and
and 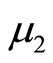 respectively such that
respectively such that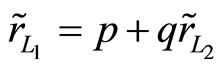 and
and , if r,
, if r,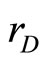 and
and 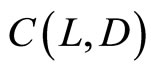 are independent of
are independent of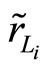 , then we have
, then we have
1) if 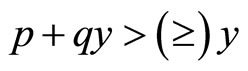 for all y, then
for all y, then  for any u such that
for any u such that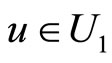 ; and
; and
2) if  such that
such that , i.e.,
, i.e., 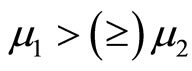 , then
, then 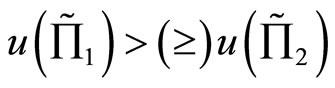 for any
for any 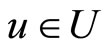 such that
such that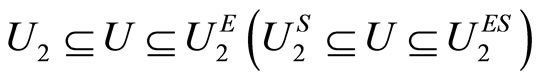 .
.
Similarly, Corollary 2 tells us that if two effective rates of returns 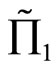 and
and 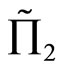 satisfy
satisfy  with
with , then the effective rate of return
, then the effective rate of return 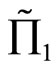 stochastic dominates the effective rate of return
stochastic dominates the effective rate of return  and hence
and hence  is preferred by FSD investors. If the effective rate of returns
is preferred by FSD investors. If the effective rate of returns 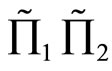 satisfying the inequality relationship as stated in part (2) of Corollary 2, then
satisfying the inequality relationship as stated in part (2) of Corollary 2, then 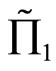 is preferred to
is preferred to 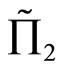 for any SSD investor.
for any SSD investor.
In part (2) of Proposition 4 and part (2) of Corollary 2, one can easily show that  has a bigger mean and smaller variance than
has a bigger mean and smaller variance than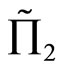 . Hence, we obtain the following corollary:
. Hence, we obtain the following corollary:
Corollary 3:
1) For the random profits  and
and 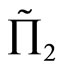 with means
with means 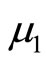 and
and 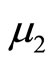 and variances
and variances 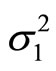 and
and  respectively such that
respectively such that 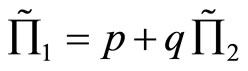 if
if  and
and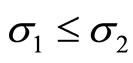 , then
, then 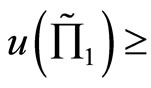
 for any
for any 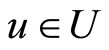 such that
such that 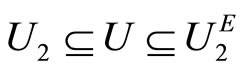 or
or .
.
2) For the effective rates of returns 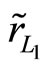 and
and 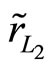 with means
with means 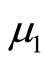 and
and 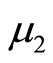 and variances
and variances 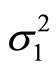 and
and 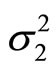 respectively such that
respectively such that 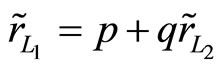 and
and 
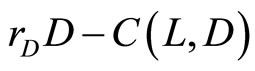 , if r,
, if r, 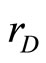 and C(L, D) are independent of
and C(L, D) are independent of 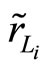 and if
and if 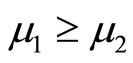 and
and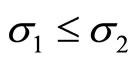 , then
, then 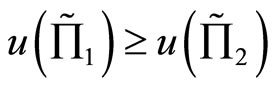 for any
for any 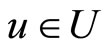 such that
such that 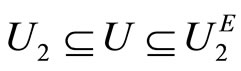 or
or 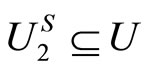
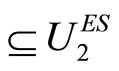 .
.
It is common to compare the assets in the s-m indifference curves diagram if one applies the mean-variance (mean-standard deviation) approach. In this connection, we can rewrite Proposition 4 and Corollary 2 in the following corollaries to start its relationship in the s-m indifference curves diagram:
Corollary 4: For the random profits  and
and  with means
with means 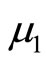 and
and 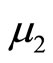 and variance
and variance  and
and  respectively such that
respectively such that 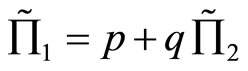 in the s-m indifference curves diagram1) if
in the s-m indifference curves diagram1) if 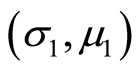 and is in the north of
and is in the north of , the random profit
, the random profit 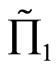 is preferred to the random profit
is preferred to the random profit  for any FSD risk investor; and 2) if
for any FSD risk investor; and 2) if 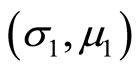 and is in the north-west of
and is in the north-west of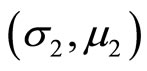 , the random profit
, the random profit 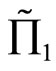 is preferred to the random profit
is preferred to the random profit  for any SSD risk averter.
for any SSD risk averter.
Corollary 5: For the effective rates of returns 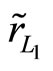 and
and 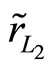 with means
with means  and
and 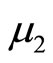 and variances
and variances  and
and  respectively such that
respectively such that 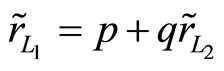 and
and

in the s-m indifference curves diagram, if r, 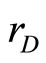 and C(L, D) are independent of
and C(L, D) are independent of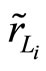 , then 1) if
, then 1) if 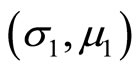 and is in the north of
and is in the north of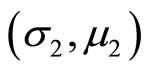 , the random profit
, the random profit 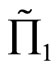 is preferred to the random profit
is preferred to the random profit  for any FSD risk investor; and 2) if
for any FSD risk investor; and 2) if 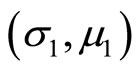 and is in the north-west of
and is in the north-west of , the random profit
, the random profit 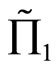 is preferred to the random profit
is preferred to the random profit 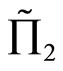 for any SSD risk averter.
for any SSD risk averter.
The above corollaries provide an easy way to compare different random profits and compare different the effective rates of returns. One can simply plot their means and standard deviations in the s-m indifference curves diagram. Those in the north are preferred to those in the south for any FSD risk investor; and those in the northwest are preferred to those in the south-east for any SSD risk averter.
4. Concluding Remarks
In the paper, analyses have been conducted on optimal hedging of a competitive banking firm where credit risks in the economy are tradable on a financial risk-sharing market. Specifically, it has been shown that a (µ, σ)-riskaverse bank management revises its optimal hedging policy according to its preference, i.e., its intensity of risk aversion. The elasticity of risk aversion determines whether or not a bank management decreases or increases the optimum hedge ratio when parameters of the decisionmaking process changes [26-28].
Furthermore, reviews have been made on the meanvariance (mean-standard deviation) approach together with extensions on the results derived from the literature. Lastly, comments have been made on finding in the literature which states that the firstand second-degree stochastic dominance efficient sets are equal to the mean-variance efficient set.
5. References
[1] X. Freixas and J.-C. Rochet, “Microeconomics of Banking,” 2nd Edition, MIT Press, Cambridge, 2008[2] J. Bessis, “Risk Management in Banking,” 3rd Edition, Wiley & Sons, Chichester, 2009.
[3] Th. C. Wilson, “Portfolio Credit Risk,” Federal Reserve Bank of New York Economic Policy Review, Vol. 4, No. 3, 1998, pp. 71-82.
[4] F. A. DeRoon, T. E. Nijman and B. J. M. Werker, “Currency Hedging for International Stock Portfolios: The Uselfulness of Mean-Variance Analysis,” Journal of Banking & Finance, Vol. 27, No. 2, 2003, pp. 327-350. doi:10.1016/S0378-4266(01)00251-5
[5] H. Schneeweiß, “Entscheidungskriterien bei Risiko,” Springer, Berlin, 1967.
[6] J. Meyer, “Second Degree Stochastic Dominance with Respect to a Function,” International Economic Review, Vol. 18, No. 2, 1977, pp. 476-487. doi:10.2307/2525760
[7] J. Meyer, “Two-Moment Decision Models and Expected Utility Maximization,” American Economic Review, Vol. 77, No. 3, 1987, pp. 421-430.
[8] A. Löffler, “Variance Aversion Implies µ-σ²-Criterion,” Journal of Economic Theory, Vol. 69, No. 2, 1996, pp. 532-539.
[9] Z. Bar-Shira and I. Finkelshtain, “Two-Moments Decision Models and Utility-Representable Preferences,” Journal of Economic Behavior & Organization, Vol. 38, No. 2, 1999, pp. 237-244. doi:10.1016/S0167-2681(99)00008-6
[10] W.-K. Wong and C. K. Li, “A Note on Convex Stochastic Dominance Theory,” Economics Letters, Vol. 62, No. 3, 1999, pp. 293-300. doi:10.1016/S0165-1765(98)00231-6
[11] M. Ormiston and E. Schlee, “Mean-Variance Preferences and Investor Behavior,” Economic Journal, Vol. 111, No. 474, 2001, pp. 849-861. doi:10.1111/1468-0297.00662
[12] A. Wagener, “Prudence and Risk Vulnerability in TwoMoment Decisions Models,” Economics Letters, Vol. 74, No. 2, 2002, pp. 229-235. doi:10.1016/S0165-1765(01)00541-9
[13] U. Broll, J. E. Wahl and K.-W. Wong, “Elasticity of Risk Aversion and International Trade,” Economics Letters, Vol. 92, No. 1, 2006, pp. 126-130. doi:10.1016/j.econlet.2006.01.031
[14] W.-K. Wong and C. H. Ma, “Preferences over Location-Scale Family,” Economic Theory, Vol. 37, No. 1, 2008, pp. 119-146. doi:10.1007/s00199-007-0254-3
[15] H. M. Markowitz, “Portfolio Selection, Cowles Foundation Monograph 16,” Wiley, New York, 1959.
[16] J. Von Neumann and O. Morgenstern, “Theory of Games and Economic Behavior,” John Wiley, New York, 1947.
[17] G. Hanoch and H. Levy, “Efficiency Analysis of Choices Involving Risk,” Review of Economic Studies, Vol. 36, No. 3, 1969, pp. 335-346. doi:10.2307/2296431
[18] D. P. Baron, “Information, Investment Behavior, and Efficient Portfolios,” Journal of Financial and Quantitative Analysis, Vol. 9, No. 4, 1974, pp. 555-566. doi:10.2307/2329760
[19] H. Levy, “Two-Moment Decision Models and Expected Utility Maximization: Comment,” American Economic Review, Vol. 79, No. 3, 1989, pp. 597-600.
[20] H.-W. Sinn, “Expected Utility, µ-σ Preferences, and Linear Distribution Classes: A Further Result,” Journal of risk and uncertainty, Vol. 3, No. 3, 1990, pp. 277-281. doi:10.1007/BF00116785
[21] A. W. Roberts and D. E. Varberg, “Convex Functions,” Academic Press, New York, 1973.
[22] G. A. Whitmore, “Third-Degree Stochastic Dominance,” American Economic Review, Vol. 60, No. 3, 1970, pp. 457-459.
[23] J. Hadarand and W. R. Russel, “Stochastic Dominance and Diversification,” Journal of Economic Theory, Vol. 3, No, 3, 1971, pp. 288-305. doi:10.1016/0022-0531(71)90024-X
[24] L. Tesfatsion, “Stochastic Dominance and Maximization of Expected Utility,” Review of Economic Studies, Vol. 43, No. 2, 1976, pp. 301-315. doi:10.2307/2297326
[25] D. Stoyan, “Comparison Methods for Queues and Other Stochastic Models,” John Wiley, New York, 1983.
[26] G. Davis, “Income and Substitution Effects for MeanPreserving Spreads,” International Economic Review, Vol. 30, No. 1, 1989, pp. 131-136. doi:10.2307/2526553
[27] M. S. Kimball, “Standard Risk Aversion,” Econometrica, Vol. 61, No. 3, 1993, pp. 589-611. doi:10.2307/2951719
[28] H.-W. Sinn, “Economic Decisions under Uncertainty,” North Holland, Amsterdam, 1983.

